长苞铁杉(Tsuga lorgibracteata)是我国第四纪冰川期遗留下来的特有珍稀古老植物(林金星等，1995)。由于人为破坏和更新困难，正处于濒危状态，列为国家三级保护植物(国家环境保护局等，1987)。福建省天宝岩自然保护区保存有一片以长苞铁杉为优势种的混交林，面积约72 hm²。本文在对其种群林分生长调查基础上(吴承祯等，2000a；2000b)，分析其优势度增长规律，为该区域长苞铁杉种群的生长条件、群落演替及稳定性评价和保护提供科学依据。

1 研究区域概况

福建省天宝岩自然保护区位于福建省永安市，东经117°31′~117°33.5′，北纬25°55′~25°58′，面积约1 976.5 hm²。气候属亚热带东南季风气候型，四季分明，水热条件优越。年均气温23℃，绝对最低温-11℃，绝对最高温40℃，无霜期290 d左右，年均降水量2 000 mm，全年>10℃的活动积温4 520~5 800℃，持续天数225~250 d。月均空气相对湿度80%左右。保护区的山体为戴云山系余脉，山势陡，海拔680~1 604.8 m，区内大部分面积为砾岩和石灰砂，土层较薄，自然生态条件比较脆弱，土壤的垂直带谱大致是海拔800 m以下为红壤，800~1 350 m为黄红壤，1 350 m以上为黄壤，土壤呈酸性反应。

长苞铁杉群落外貌整齐，色彩暗绿，林内阴暗湿润，土层厚，表土质地松软，枯枝落叶层厚3~5 cm，为中亚热带山地垂直地带性植被类型。长苞铁杉主要伴生树种有甜槠(Castanopsis eyrei)、杉木(Cunninghamia lanceolata)、木荷(Schima superba)、深山含笑(Michelia maudiae)、薯豆(Elaeocarpus japonica)、小叶青冈(Cyclobalanopsis myrsinaefolia)及冬青(Ilex purpurea)等。

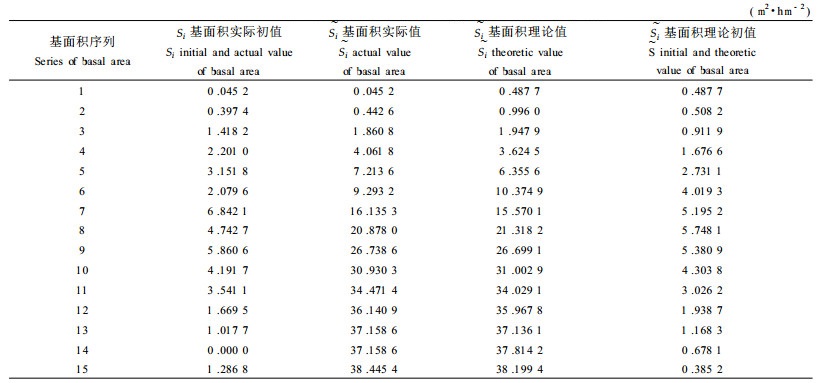
2 研究方法 2.1 调查方法

选择具代表性的长苞铁杉分布地段没置6块600 m²的样地，对每样地长苞铁杉每木检尺(胸径≥4 cm)，记录其树高、胸径、冠幅等指标和胸径在4 cm以下长苞铁杉幼苗幼树的株数，并记录样地的生境条件、植被情况。每一样地挖3个土壤剖面取土样带回室内分析。天宝岩自然保护区内的长苞铁杉林主要分布于海拔1 350~1 500 m地带，为天然林，基本保持原始状态。树干解析表明，其胸径生长与年龄之间存在一定对应关系，因此，可以认为长苞铁杉种群结构满足生态学中“空间代时间”的基本条件。为此，以其种群基面积作为种群优势度的数量指标，采用空间序列代替时间序列法(曹广侠，1991；洪伟等，1997；苏智先，1993)，将种群依胸径大小分级，每级间隔为5 cm，把种群的径级从小到大看成时间顺序关系(曹广侠，1991；洪伟等，1997)，即第一径级对应T=1时的时间；第二径级对应T=2时的时间；……；第n径级对应T=n时的时间。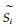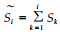令时间单位为径级年，计算样地各径级林木基面积数值之和为各径级基面积的初值，再换算成单位面积(hm²)各径级基面积的初值(S_i)，种群在第i径级的累计基面积记为，即。于是得到时间单位为径级年的时序关系所对应的长苞铁杉种群的基面积数值，据此研究其优势度增长动态。

2.2 建模方法

在有限的生存空间，任何生物种群的增长均是有限的，定量描述这一过程有Verhulst(苏智先，1993)首先提出的著名的Logistic方程：

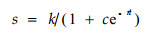
(1)

式中，s为种群大小；t为时间；k为环境容纳量；r为内禀增长率。

Smith(1963)通过对实验种群个体增长率的直接观测，发现种群增长受密度制约且是一条下凹的曲线，基于种群生存和增长两者对环境资料的需求变化，提出对Logistic方程进行扩充：

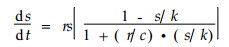
(2)

式中，c为参数(正值)。由于(2)的制约函数f_s=(1-s/k)/(1+(r/c)(s/k))中分母大于1，必有制约函数f_s＜(1-s/k)，所以(2)式只能描述下凹增长曲线。

崔启武等(1982)提出只能描述上凸Logistic增长曲线的非线性制约效应的种群增长模型：

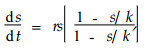
(3)

式中，k′为营养参数，(2)、(3)式在一般情况下并不存在解析解，也给模型的参数估计带来了困难。为此，张大勇等(1985)引入自适应调整的种群增长模型：

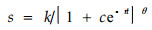
(4)

式中，θ为一个取值为(0，+∞)的常数，具有能兼容各种密度制约机制。

刘金福等(1998)在研究格氏栲种群优势度增长动态规律时提出更为通用的模型：

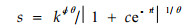
(5)

式中，θ、φ为密度制约参数，由于增加两个参数，该模型不仅刻画了密度制约机制而且通过多个参数的互相调整使其模拟效果更好。

笔者(吴承祯等，2000c)曾推导一个追踪种群生物量未达饱和时的植物种群优势度在生长过程中的变化规律模型：

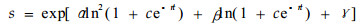
(6)

式中，s为植物种群优势度：α、β为环境制约参数；r为内禀增长率；e^γ为环境容纳量；c为常数；α、β、r、c、γ为待定参数且与植物本身生物学与生态学特性有关。它包融了Logistic模型、Smith模型、Gompertz模型、崔-Lawson、张-Logistic模型及刘-Logistic模型(吴承祯等，2000c)。

3 长苞铁杉种群优势度增长模型的比较

本文以长苞铁杉种群优势度增长观测数据拟合几种经典种群增长模型，利用拟合残差平方和Q进行比较。非线性模型拟合的方法很多(吴承祯等，1997；潘辉等，1992；吴承祯等，1999)，本文应用遗传算法(吴承祯等，1997)进行最优拟合。

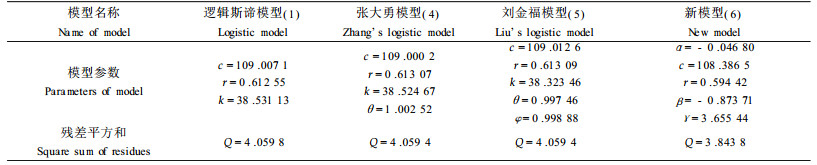
由于模型(2)、(3)的隐式解结构是一致的，而且一般不含显式解，为此，用(1)、(4)、(5)、(6)式的显式解进行遗传算法最优拟合(表 2)。由表 2可以看出，模型(6)拟合残差平方和Q比模型(1)、(4)、(5)均小，拟合精度得到明显提高，而模型(1)、(4)、(5)模拟效果基本一致。不同模型的比较进一步说明了笔者所提出的种群增长模型(吴承祯等，2000c)的适用性和科学性，因此，模型(6)是珍稀濒危植物长苞铁杉种群优势度增长规律的一个较好的表达式。当然，这与模型本身特性有关，因为其它模型仅为其一个特例(吴承祯等，2000c)。

4 结果与分析

笔者提出的描述种群增长模型(6)，其模型有5个参数α、β、γ、c、r。至于参数的求解，可先给定初值α=0、β=-1，这样将其转化为种群增长的Logistic模型s=k/(1+ce^-rt)。依据表 1中空间单位为径级的时序关系所对应的林木种群的基面积数值，采用遗传算法建立长苞铁杉种群基面积增长的Logistic模型：

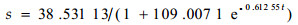
(7)

或

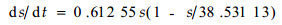
即环境容纳量为38.531 1 m²·hm^-2，内禀增长率为0.612 55。因此利用模型(7)的参数解，可得方程(6)参数的初值：γ=lnk=ln(38.531 1)=3.651 5、c=109.007、α=0、r=0.612 55、β=-1。利用遗传算法进行参数优化，得到优势度增长模型的残差平方和为3.843 8，优化后模型为：

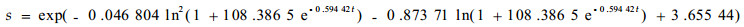
(8)

此方程相关指数为0.999 4，可见回归效果较理想。模型(8)表明长苞铁杉种群优势度增长的内禀增长率为0.594 42，同时模型(8)克服了模型(7)所具有的曲线特性，即模型(7)只能描述种群最大增长速率在环境容纳量一半处达到的事实，而模型(8)则能描述实际最大增长速率在环境容纳量一半前、一半处及一半后出现的现象(吴承祯等，2000c)。长苞铁杉种群增长各径级基面积理论值及理论初值模拟计算表明珍稀濒危植物长苞铁杉种群优势度增长的实际最大增长速率在第8径级附近，即其优势度最大增长速率在环境容纳量的一半之后(表 1)而非经典Logistic方程环境容纳量一半处。

经数学证明，长苞铁杉种群基面积增长的新模型在其平衡位置是全局稳定，模型的平衡位置是基面积为e^γ＝38.684 7 m²·hm^-2的点。因此，模型(8)所描述的种群基面积增长规律，将保持其在各自平衡位置全局稳定。在种群优势度增长规律模型中，内禀增长率r是一个与树种生长特性有关的参数，r越大，表示种群增长越迅速，其受树种生物生态学特性影响。长苞铁杉种群优势度增长的内禀增长率为0.594 42，较黄山松、马尾松、丝栗栲等小(洪伟等，2000)，这是由长苞铁杉种群生物、生态学特性所决定。长苞铁杉种群生长缓慢，尤早期幼龄时生长更慢，平均生长轮宽1~2 mm，到15 a左右才有所加快，但平均生长轮宽度也仅3~4 mm，从而使得长苞铁杉种群内禀增长率较小。而对于环境制约参数α和β，则表现为参数α比格氏栲种群优势度增长相应的α大(-0.346 846)，而β值则比格氏栲种群小(-0.469 923)(吴承祯等，2000c)，表明长苞铁杉种群生长受环境制约较大，尤其表现在种内竞争上。这是由于长苞铁杉为喜光、耐贫脊的阳性针叶植物，无论在哪一类群落中它都必然处于群落的最上层，在林冠下无法与生长迅速的耐阴阔叶树种竞争。

5 讨论

应用4个具一定代表性的种群数量增长动态模型对珍稀濒危植物长苞铁杉种群优势度增长规律进行描述，结果表明经典Logistic模型、张-Logistic模型、刘-Logistic模型三者效果基本一致，而笔者(吴承祯等，2000c)提出的自适应增长模型拟合效果最好，残差平方和得到明显减小，能较好地描述长苞铁杉种群优势度增长规律。因此本研究一方面分析了长苞铁杉种群优势度增长规律；另一方面进一步验证了笔者(吴承祯等，2000c)所提出的种群增长模型的适用性。根据所建立的长苞铁杉种群优势度增长规律模型，计算得到其环境容纳量为38.684 7 m²·hm^-2。长苞铁杉种群优势度增长模拟表明其优势度最大增长速率在第8径级左右达到，即胸径为40 cm左右，说明当种群胸径小于40 cm时，种群基面积随时间增长而增长，其增长加速度为正；当胸径处于40 cm左右时，其增长速度达到最大，加速度为零，这是基面积S型曲线的拐点；胸径超过40 cm时，种群基面积增长速度减慢，加速度为负。因此，我们不仅要禁止任何形式的砍伐和破坏；而且应遵循其种群优势度增长规律采用人工干预措施，辅助长苞铁杉林幼苗幼树生长，确保种质资源。

本文用于描述长苞铁杉种群优势度增长规律的种群增长模型参数较经典Logistic模型相对较多，但目前非线性参数最优拟合方法较多，有麦夸方法、3次设计(潘辉等，1992)、改进单纯形法(吴承祯等，1999)和遗传算法(吴承祯等，1997)等，本文采用遗传算法进行模型参数最优拟合，效果较理想且易于在计算机上实现。