植物种间联结关系的研究约有100年的历史，国内外学者提出了多种公式：I₁=(ad-bc)/(ad+bc)(Yule, 1912), I₂=2a/(2a+b+c)(Dice, 1945), I₃=(a+b)(a+c)/a(Margalef, 1958), 上述这些公式均没有考虑每一样方的种群数量，而只检查种是否出现；无疑这些指数受样方大小的影响是很大的。吴大荣(1997)提出了与每一样方内种群数量相关的联结度指数测定方法。这些指数的取值均在[-1，1]之内，有归一化特点，比较直观; 但这些联结度指数都难以建立与显著性检验的统计量的关系，这样就使联结度与联结关系是否显著的检验分离，即定性分析与定量分析的分离。联结度指数与显著性检验统计量之间不能直接换算，联结度指数受样方大小的影响较大，这是长期以来一直困扰生态学工作者的一个重要问题，而且在进行生态调查前是难以知道样方大小的。Schloter(1984)提出了方差比率法，但仍未考虑各样方中种群数量，仅涉及种是否出现。

笔者设计了一系列的联结度指数，可以进行统计量与联结度指数之间的互相转换，能在一定程度上消除样方大小对联结度指数的影响，并给出了通用的显著性检验统计量。

1 经典的联结度检验统计量

假设从大量可能单位的种群中随机地布设N个样方，令研究的两个种标记为种1和种2；对每个样方记下它是否包含包含种1和种2，包含分为四种情况：两种同时包含，只包含种1，只包含种2，两个种均不包含。这样，观察的频率可以构成一个2×2形式的表达式：

(1)

其中a:包含种1且包含种2的样方数; b:包含种1但不包含种2的样方数；c:包含种2但不包含种1的样方数；d：两个种均不包含的样方数。

如前所述，有多种联结度指数的定义(Dice，1945; Yule，1912; Margalef, 1958)。在使用联结度指数时，无论使用哪一种，而联结关系的显著性检验大多应用了(2)式所定义的统计量(郭志华等，1997；李建民等，2001；廖军等，2000；孙学刚等，1998; 史作民等，2001；王峥峰等，1997；周先叶等，2000; 张文辉等，1998)，使用χ²统计量则是(2)式统计量的变型，本质上仍是(2)式定义的统计量。所以，本文称(2)式定义的统计量为经典联结度检验统计量：

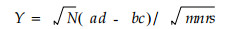
(2)

γ用于检验种间联结性。容易证明，当N充分大时，γ趋于标准正态分布。两个种的联结度指数：

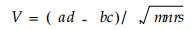
(3)

注意到γ本身就是联结度，取值范围为(-∞，+∞)，V的取值范围为[-1，1]。而V的计算仅涉及(1)式中的变量，没有对抽样样方中的个体数进行分辨，而样方大小正与个体数有关，所以V受抽样样方大小的影响较大，它就是经典的点相关联结度指数。从理论上讲，只有抽样样方平均个体数适中时此指数才有效。所以要消除样方大小对联结指数的影响，必须对个体数进行分辨。为此笔者提出将一个样方内的种间联结度称为局部联结度，它是样方内两个种的个体数的函数，而将所有样方的局部联结度的算术平均数称为联结度。

除了使用χ²统计量对种间联结的显著性进行检验外，t分布也常用于种间联结性检验(郑元润，1998；邹惠渝等，1999)。在有些研究中使用了多种方法进行检验(阳小成，1994)。

2 联结度指数模型

对于(1)式中所提到的种1和种2，在每一个样方内定义如下局部联结度的一般形式为：

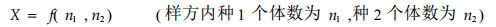
(4)

其中f为n₁, n₂的确定性函数，它是对两个种在特定样方内的局部联结度的定义式。

假设共抽取了N个样方，产生了局部联结度的随机变量序列为X₁，X₂，…，X_N，这些随机变量是独立同分布的，则有：

(5)

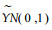
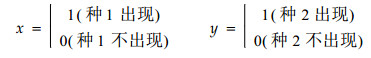
对于f(n₁, n₂), 只要E(X)和Var(X)有限，根据大数定理，则有：当n→∞时，，可见γ趋于标准正态变量。现在来证明，(2)式和(5)式是等价的。构造随机变量：

根据(1)式的定义有：

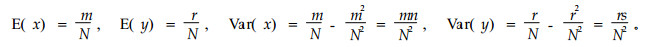
构造随机变量：

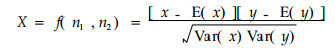
(6)

显然，对于任意一个抽样样方便有一个这样的随机变量，共抽取了N个样方，产生了随机变量序列为X₁，X₂，…，X_N，这些随机变量是独立同分布的，且有：

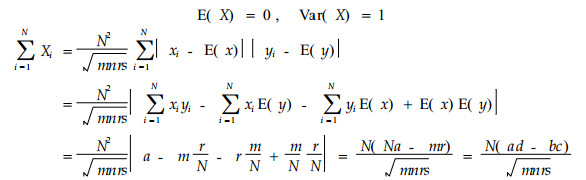
令

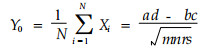
(7)

将(7)式代入(5)式有

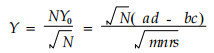
(8)

可见(8)式与(2)式完全一样，(7)与(3)式完全一样，从而我们已经证明了种间联结指数V((3)式中V)是独立同分布的随机变量的算术平均数的这一事实，同时也证明了经典联结度指数检验统计量(2)式是(4)式推导出的一个特例。所以，对联结度指数的构造归结为对局部联结度指数f(n₁, n₂)的构造。而且这些联结度指数都可以用标准正态分布来进行显著性检验。

3 四种联结度指数的构造

从前面的证明可知，种间联结度是局部联结度的平均数，如果局部联结度定义很简单，其计算过程就会很简单，下面的局部联结度定义就象计数那么简单。

在下面的证明中，X为(4)式定义的局部联结度指数，γ₀为(10)式定义的联结度指数，γ为(5)式定义的趋于标准正态分布的统计量。

3.1 f(n₁, n₂)的第1种形式

(9)

令

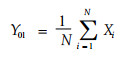
由(5)式可得

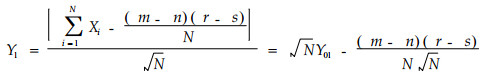
(10)

当N充分大时，γ₁趋于标准正态分布。从上述推导可知γ₁的计算非常简单，γ₀₁实际上是一个计数统计量，整个计算过程可以用计算器完成，但需要注意的是γ₁有不太稳定的缺点。

3.2 f(n₁, n₂)的第2种形式

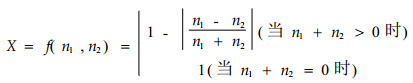
(11)

吴大荣(1997)研究了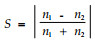, 当S=0时两个种为最大联结，S＝1时两个种无联结，但他没有涉及用S进行显著性检验的问题，当涉及检验时用(11)式更为方便。

由于假设两个种的分布是随机性格局且两个种相互独立，则n₁, n₂的分布满足下式：

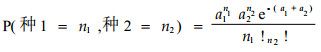
(12)

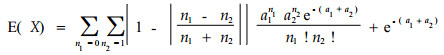
(13)

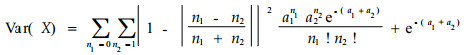
(14)

其中a₁为种1在样方中的平均株数，a₂为种2在样方中的平均株数。

显然(13)、(14)式是均值和方差的定义式，容易证明(11)式定义的局部联结度指数，其均值和方差是有限的，所以X的独立同分布序列仍然满足大数定理，应用(5)式可构造检验统计量，由于这里的E(X)，Var(X)不能简化形式，所以它的统计量形式与(5)式是一样的。

这种形式的局部联结度指数计算过程较复杂，必须通过计算机来完成计算过程。

3.3 f(n₁, n₂)的第3种形式

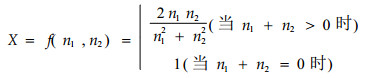
(15)

容易证明2n₁n₂≤n₁²+n₂²，所以0≤f(n₁, n₂)≤1，可以证明以(15)式为局部联结度的随机变量X有有限的均值和方差。其它方面的推导与第二种形式局部联结度指数一样。

3.4 f(n₁, n₂)的第4种形式

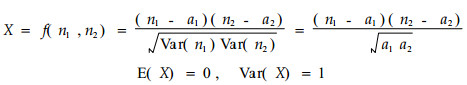
(16)

令

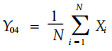
由(8)式可得

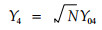
(17)

显然(16)式是一个线性相关性指数，而且用到了泊松分布(假设两个种均是随机性格局)的均值与方差相等的事实。(17)式的表达虽简单，而γ₀₄的求取较为复杂。容易看出，(16)式定义的联结度是一种线性相关性定义，但由于n₁，n₂的取值范围没有限定，X、γ₀₄的取值范围也不能限定，虽然如此，在后面的实际应用中发现γ₀₄的绝对值一般不超过1，而且γ₀₄和γ₄相当稳定，且受样方大小的影响很小。

4 各种联结度指数的应用和比较

为了对比各种联结度指数，笔者应用帽儿山林场10块固定标准地来计算相应指数。在固定标准地中，每一株树的位置和树种都已调查，并应用GIS建立了点专题，图 1是应用的固定标准地中较典型的一块。

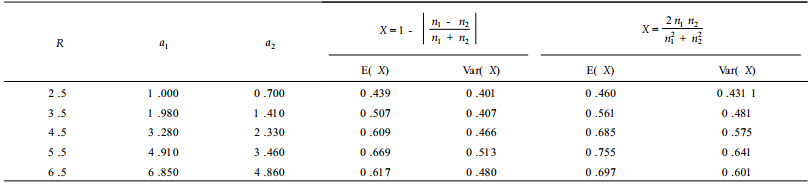
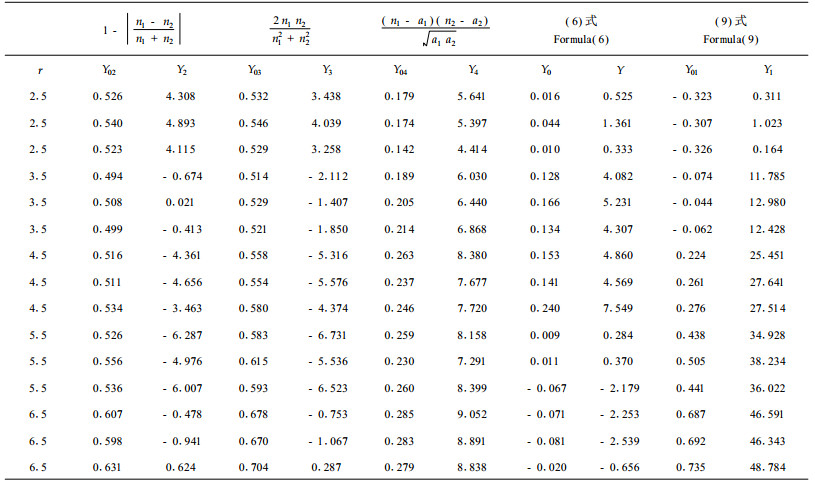
13号固定标准地位于尖砬沟8林班2小班，面积0.06 hm²，图 1中5代表水曲柳(Fraxinus mandshurica)，11代表裂叶榆(Ulmus laciniata)，这里对这两个树种进行计算，对各种联结性指标进行比较，过程如下：设定样圆半径r；在固定标准地的范围内产生一个随机点，并以半径r产生一个样圆，若样圆全部被包含在固定标准地内则进行下一步，否则退回起点; 对固定标准地内的树种5和11，计算在样圆内的株数；根据样圆内两个树种的株数求局部联结度; 计算局部联结度的平均数γ₀；计算联结度的检验统计量γ。表 1中a₁, a₂是种1和种2在样圆中的平均数，E(X)，Var(X)是根据相应的局部联结度定义计算的均值和方差。

从表 2可见，对不同的样圆半径计算了联结度，相同的样圆半径分别计算了3次，由于样圆位置是随机的，三个相同的样圆半径，其结果有差别。第4种局部联结度指数最为稳定，虽然随样圆半径的增大有所增加，但增幅不大，而且符号保持为正。

从表 2可见，经典联结度对样圆半径r的影响很大，而且不是随r增大而单调增大。当r=6.5 m时，联结度改变了符号，这是因为(1)式中a随r增大而增大，而d随r增大而降低，这样ad会反而降低。

从表 2可见，第1种局部联结度指数受r的影响幅度很大，但它随r的增大而增大，基本保持单调性。

第2、3种局部联结度指数受r的影响较大，而且符号和幅度变化均较大，只有事先知道其合适的样圆大小才能使用。

特别需要注意的是：联结度并非接近1时才是显著的，因为标准正态分布的95%置信区间是[-1.96，1.96]，从表 2中可见当γ₀＞0.1时，γ早就不在置信区间内了。这是因为γ是样本大小N的函数，当N很大时，γ₀很小也可能使γ超过域值水平，所以，在实际应用时不能仅看局部联结度指数的算术平均数γ₀的大小，而要看统计量γ的绝对值是否大于1.96。

笔者还对其它不同的种进行计算表明，对于两个种的相对个体数量相差特别悬殊的情况下进行联结度检验是不真实的。从表 2可见，无论哪一种联结度指数的适应性都是有限的，过大或过小的样方大小均会导致错误的判断。

5 结论

联结度指数模型有广泛的概括性，经典联结度指数检验统计量是这一模型的特例。

本文提出的第四种局部联结度指数有较好的稳定性，这一指数受样圆(或样方)大小的影响较小，有广泛的适用性；但是，无论那一种联结度指数其适应性均是有限的，过大或过小的样方大小均会导致错误的判断。