文章信息
- 李永慈, 唐守正, 李海奎.
- Li Yongci, Tang Shouzheng, Li Haikui.
- 用两阶段度量误差模型方法和ForStat软件进行模型整合
- Model Integration Using the Method of Two-stage Error-in-variable and the Soft of ForStat
- 林业科学, 2004, 40(2): 75-78.
- Scientia Silvae Sinicae, 2004, 40(2): 75-78.
-
文章历史
- 收稿日期:2002-08-26
-
作者相关文章
2. 中国林业科学研究院资源信息研究所 北京 100091
2. The Institute of Forest Information Research, Chinese Academy of Forestry Beijing 100091
在系统生态学中,存在大量不同时空尺度上的动态生态模型。一般小尺度模型比较精细,更能反映局部生态过程的细微变化,对外界影响的反映更敏感。大尺度上的模型比较综合,更能反映生态系统的“平均”性质。如何将小尺度的精细模型编入大尺度的综合模型正在越来越多地引起研究者的兴趣。已有大量文献报道不同尺度模型或模型不同组分关系的研究。此类问题在不同文献中被称为“变尺度”、“联接”、“累积”、“拆分”或“整体性”。这样做的问题是用常规方法得到的参数往往是不相容的,也就是说,从大尺度的综合模型得到的参数与从小尺度的精细模型得到的参数是不同的。Tang等(2002)给出了进行模型整合的两阶段度量误差模型方法、它的数值算法以及Matlab程序,利用这种方法得到的参数是相容的,有效解决了模型整合中参数相容性问题。本文利用文献(Tang et al., 2002)表 1的实验数据,研究了同龄林分的年龄X、平均单株胸径Y1 (cm)和平均单株材积Y2 (m3)的关系模型的整合问题。所有计算和绘图都是利用中国林科院资源信息研究所森林经理和林业统计研究室开发的ForStat统计之林软件进行的。
1 选择模型原形和变量变换为了研究同龄林分的年龄X、平均单株胸径Y1(cm)和平均单株材积Y2(m3)的关系模型的整合问题,首先进行模型选择。对于胸径(D)和年龄(X)的关系、材积(V)和胸径的关系分别选择广泛应用的里查德模型和幂函数模型:
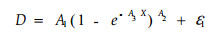
|
(1) |
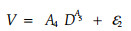
|
(2) |
这里A1、A2、A3、A4、A5是参数,ε1和ε2是随机误差。从模型可以看出,X是没有误差的变量,D和V是有误差的变量。我们知道参数估计是在随机误差服从独立同分布的条件下进行的,根据林业测量的经验,可以认为随机误差满足独立性条件。为了保证同分布的条件,分别将模型(1)和(2)做对数变换得模型(3)和(4)
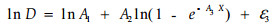
|
(3) |
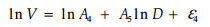
|
(4) |
|
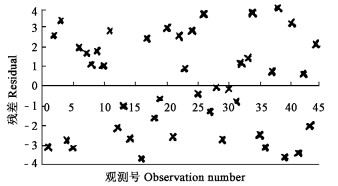
图 1 模型(1)的残差图 Fig. 1 Residual of model (1) |
|
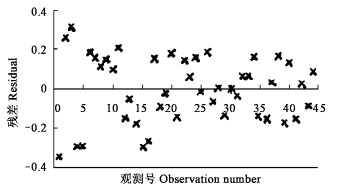
图 2 模型(3)的残差图 Fig. 2 Residual of model (3) |
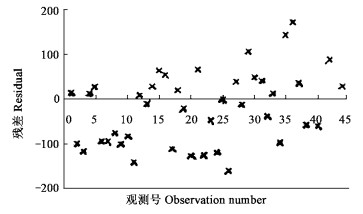
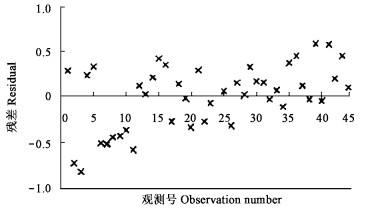
将模型(1)和(3)的残差进行比较,两者差异不显著,我们取模型(3)作为直径和年龄的关系模型。比较模型(2)和模型(4)的残差图可见模型(4)优于模型(2),因此我们选择模型(4)作为材积和直径的关系模型。
|
图 3 模型(2)的残差图 Fig. 3 Residual of model (2) |
|
图 4 模型(4)的残差图 Fig. 4 Residual of model (4) |
在模型(3)和(4)中引进Y1=lnD, Y2=lnV, ln(A1)仍记为A1,ln(A4)仍记为A4。最终模型形式为:
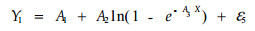
|
(5) |

|
(6) |
两种常用的模型参数的估计方法分别为:第一种方法是用两个方程分别估计参数,第二种方法是将方程(5)代入方程(6),合并常数后得
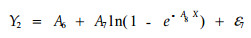
|
(7) |
然后再由方程(7)估计参数。
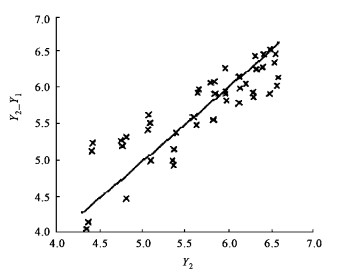
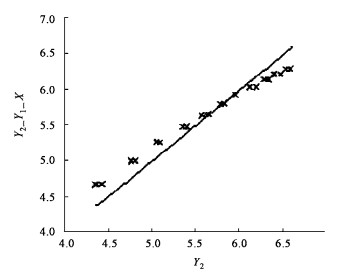
第一种方法的参数估计结果为:模型(5):相关指数= 0.741 6,A1=3.5023,A2=1.279 9,A3=0.048 2。模型(6):相关指数= 0.745 2,A4=0.548 3,A5=1.816 5。做Y2的实测值与预测值对比图(图 5、6),其中Y2_Y1表示用Y1估计Y2得到的Y2的估计值,Y2_Y1_X表示用X估计Y1后再用Y1估计Y2得到的Y2的估计值。可以看出Y2_Y1_X是明显有偏的。
|
图 5 Y2估计值(Y2_Y1)与观测值的对比图 Fig. 5 Comparison of observation Y2 and estimation (Y2_Y1) |
|
图 6 Y2估计值(Y2_Y1_X)与观测值的对比图 Fig. 6 Comparison of observation Y2 and estimation (Y2_Y1_X) |
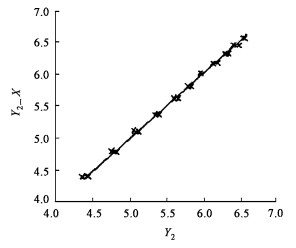
第二种方法的参数估计结果为:相关指数= 0.998 2,A6=8.672 9,A7=2.301 5,A8=0.016 9。做Y2的实测值与预测值对比图(图 7),其中Y2_X表示用X估计Y2得到的Y2的估计值。可以看出Y2_X估计精度很高。
|
图 7 Y2估计值(Y2_X)与观测值的对比图 Fig. 7 Comparison of observation Y2 and estimation Y2_X |
这两种方法估计的参数,并且用方程(7)进行预测比用方程(5)和(6)进行预测更精确。事实上,当前一阶段子模型的输出作为后一阶段子模型的输入时,变量是内生的,因而导致估计结果是有偏的。当模型的链很长时,这种偏差不断积累,致使最终的估计结果难以置信。
3 用两阶段度量误差模型方法进行模型整合用方程(5)和(6)分别估计出的参数是局部优化的结果,与将这些子系统整合为一个系统后估计出的参数是不相同的。针对这个问题,唐守正等(1996)提出了一种称为两阶段度量误差模型(TSEM)的新方法,并给出了数值算法(Tang et al., 2001)。它与以上两种方法有本质的区别。用这种方法估计参数时,各个子系统参数的估计是同时进行而不是分别进行的,此方法同样适用于非线性联立方程组。Tang等(2002)给出了这种方法的Matlab程序,并用实例介绍了程序的使用方法。但是Matlab程序要求用户有使用Matlab的经验,限制了这种方法的广泛应用。
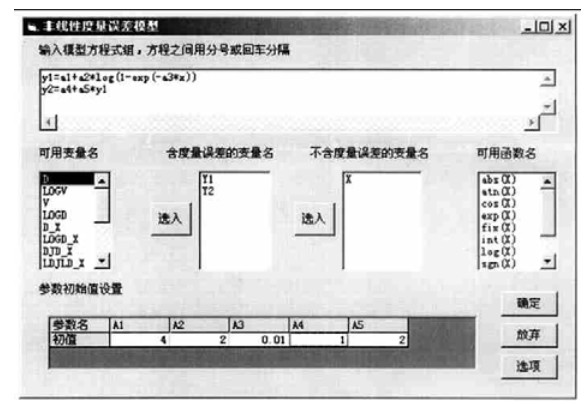
ForStat是中国林业科学院资源信息所森林经理和林业统计研究室在IBM-PC系列程序集的基础上,增加了许多近代统计方法,采用面向对象的程序设计方法和COM(组件对象模型)技术,使用可视化的集成开发环境,研制开发的一个统计分析软件。非线性度量误差模型方法是近几年统计领域的研究热点之一,为了促进两阶段度量误差模型方法的广泛应用,我们在ForStat统计之林软件中开发了一个应用程序模块,来进行非线性度量误差模型的参数估计。此模块友好的输入输出界面极大地方便了用户。有关非线性度量误差模型的理论及参数估计的数值算法,这里不再赘述。下面介绍如何用ForStat统计之林软件的两阶段度量误差模型方法对模型(5)和(6)进行整合并给出计算结果。在数据窗口输入数据,然后选择统计分析菜单下的非线性度量误差模型,调出非线性度量误差模型的方程和参数输入窗体输入方程和参数。两阶段度量误差模型参数估计结果见表 1。
|
|
|
图 8 模型和参数输入窗体 Fig. 8 The form of models and parameters input |
误差结构矩阵为:

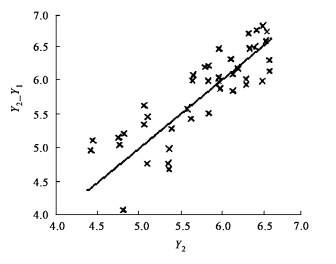
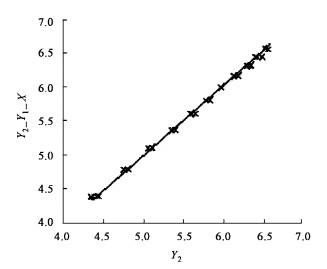
做Y2的实测值与预测值对比图(图 9、10)。可以看出用度量误差模型方法得到的Y2_Y1_X精度非常高,并且是无偏的,估计结果明显优于常规估计方法。
|
图 9 Y2估计值(Y2_Y1)与观测值的对比图 Fig. 9 Comparison of observation Y2 and estimation Y2_Y1 |
|
图 10 Y2估计值(Y2_Y1_X)与观测值的对比图 Fig. 10 Comparison of observation Y2 and estimation Y2_Y1_X |
两阶段度量误差模型理论和ForStat软件是进行模型整合的有效方法和工具。像其它算法一样,参数初始值选择很重要,如果初始值选在最优解附近算法一定能够收敛,并且收敛速度很快,否则算法很可能不收敛,或收敛速度很慢。用户可以参照通常方法得到的参数估计值来选择参数初始值。
唐守正, 李勇. 2002. 生物数学模型的统计学基础. 北京: 科学出版社.
|
唐守正, 李勇. 1996. 一种多元非线性度量误差模型的参数估计及算法. 生物数学学报, 11(3): 23-27. |
Tang Shouzheng, Wang Yonghe. 2002. A parameter estimation program for the error-in variable model. Ecological Modelling, 156(2-3): 225-236. DOI:10.1016/S0304-3800(02)00173-4 |
Tang Shouzheng, Li Yong, Wang Yonghe. 2001. Simultaneous equations, error-in variable models, and model integration in systems ecology. Ecological Modelling, 142(3): 285-294. DOI:10.1016/S0304-3800(01)00326-X |
 2004, Vol. 40
2004, Vol. 40

