在森林火灾扑救过程中，计算机支持的扑火指挥辅助决策系统是提高扑火指挥水平和扑火效率的重要手段，在林火管理水平高的国家得到普遍应用。我国也曾开展过相应研究，但由于一些基本问题没有解决，距实际应用还有一定距离。派出人员模型是其中的一个主要问题。国外对此研究较多(Hirsch et al., 1998；Fried et al., 1996)，建立了一些基于实际调查数据的模型。国内学者在最佳派出人员数量和派出人员数量经验公式等方面也开展了研究(温广玉，1994；1995；温广玉等，1995)。

派出人员模型的最终目的是要解决最合理派出人员数量的问题，由于影响因素多，扑火决策的实际数据难以获得，该问题解决难度很大。扑火指挥员派出人员决策中要考虑的因素可能包括火场的信息、自身的经验和行政因素等，然后根据一定规则计算后得到派出人员数量。尽管这种派出人员决策可能不是最佳的，初次派出的扑火力量也不一定实现控制住火灾的目标，但在扑火指挥员的头脑中是应当能实现控制火灾目标的，因此，它反映了现有林火扑救决策的真实水平。在多数情况下，上述因素和规则存在于每个指挥员的头脑中，是潜意识的，没有明确或表达出来。考虑因素的多少和规则的复杂程度与指挥员个人的经验、阅历有关。如果能揭示上述因素和相应的规则，对现有的派出人员情况进行模拟，可直接用于扑火指挥辅助决策系统中。在这些派出人员决策中，初次派出人员数量的确定是最重要的，对此过程的模拟应首先研究。

理论上讲，对该过程的模拟应建立在对实际森林火灾扑救过程记录和火场信息的基础上，但这些记录目前很难得到。为此，我们通过对黑龙江省基层扑火指挥员在不同火场情景下的初次派出人员数量进行问卷调查，获得了有关数据，建立了相应的初次派出人员数量模型，并对相关因素进行了分析。

1 材料与方法 1.1 研究地区介绍

黑龙江省位于121°11′E~135°05′E，43°25′N~53°23′N之间，面积45.4万km²，人口3 300万。大陆性气候，冬季寒冷干燥，夏季炎热多雨，春秋季多大风，空气湿度低，干燥。全省地貌分为5个区域：西北部的大兴安岭、东北部的小兴安岭、东南部的东部山地、西部的松嫩平原区及东部的三江兴凯湖平原。山地海拔高度在300~1 600 m左右，平原地区海拔在35~200 m左右。山地面积占58.9%, 平原占41.1%。省内有较大面积的森林土壤、草原土壤和森林草原土壤，属地带性土壤，同时存在着大面积的非地带性土壤。地带性植被为寒温带针叶林和暖温带针阔混交林。现有林中原始森林少，次生林多。

黑龙江省是全国森林防火的重点省份，年均森林过火面积居全国之首，是森林火灾危害最严重的地区。1980~1999年20 a共发生林火3 995次，年均200次；总过火面积为251.3万hm²，年均过火面积为12.6万hm²。森林火灾以人为火为主。

1.2 数据收集

通过问卷收集黑龙江省13个地市及其下辖县、区以及武警黑龙江省森林总队中经验丰富的扑火指挥员在45个火场情景下初次派出人员的数量(45个问题)。同时收集他们的有关背景资料作为辅助变量，包括：从事扑火工作的年数、扑火指挥工作的年数、指挥扑救地表火的次数、指挥员指挥扑救树冠火的次数和只需一次派出人员就能扑救成功的百分率等5个问题。这样调查问卷中共50个问题。调查问卷是匿名的。

火场情景是由火场面积、风力和到达火场所需时间3个因子取不同数值构成的组合，其中，初始火场面积分0.1 hm²、1 hm²、2 hm² 3种情形，到达火场所需时间分为＜20 min、20~40 min、40~60 min、60~80 min、80~100 min 5种情形，火场风力等级分为1~3级、4~6级、6级以上3种情形。在问卷设计时向有扑火指挥经验的专家咨询以确定各因子的分级情况。另对所有火场情景做如下假设：中强度地表火，扑火队员为专业扑火队员，平均每两人1台风力灭火机。对返回问卷中来自同一地方者，在地名后加数字以区分，如伊春1、伊春2等。

1.3 分析方法 1.3.1 初次派出人员数量模型的建立

对每份返回的问卷，以火场面积、火场风力等级、到达火场所需时间为自变量，派出扑火队员数量为因变量，进行多元线性回归和可转换为线性的非线性回归，建立各自的初次派出人员数量模型，称这些模型为县级模型。将返回问卷较多的黑河和伊春地区分别组成相应的地区汇总问卷，将所有问卷合并成全省汇总问卷，重复上述工作，分别建立两个地区级和全省级的派出人员模型。

1.3.2 影响派出人员数量的因素分析

指挥员的派出人员数量决策，一方面受火场情况影响，另一方面与自身的经验有关。在上述回归分析中，权重的大小反映了答卷人(指挥员)头脑中对火场面积、火场风力等级、到达火场所需时间3个因素的重视程度。对某个指挥员而言，如果赋予某个因子的权重为正值，则权重越大，表明他(她)对该因素的重视程度越高，为负值时则相反。通过对由不同问卷建立的模型中的权重进行分析，就可以揭示在派出人员决策中的3个因素对不同指挥员的影响程度。因此，对上述权重进行排序，进行百分率统计，就可得出在全省范围内3个变量对扑火派出人员决策影响的重要程度。

问卷中的背景变量反映了指挥员的扑火指挥经历。通过分析这些变量与权重的关系，就可能揭示指挥员的经验等对决策的影响。为此，计算背景变量与3个权重的相关系数，以确定它们对权重的影响。

2 结果和分析 2.1 问卷回答情况

共收回问卷18份，即18个县级数据。由于分析主要是针对单独问卷进行的，前45个问题的统计特征对独立分析影响不大，故不在此列出。答卷人的背景情况列于表 1。

2.2 派兵数量模型

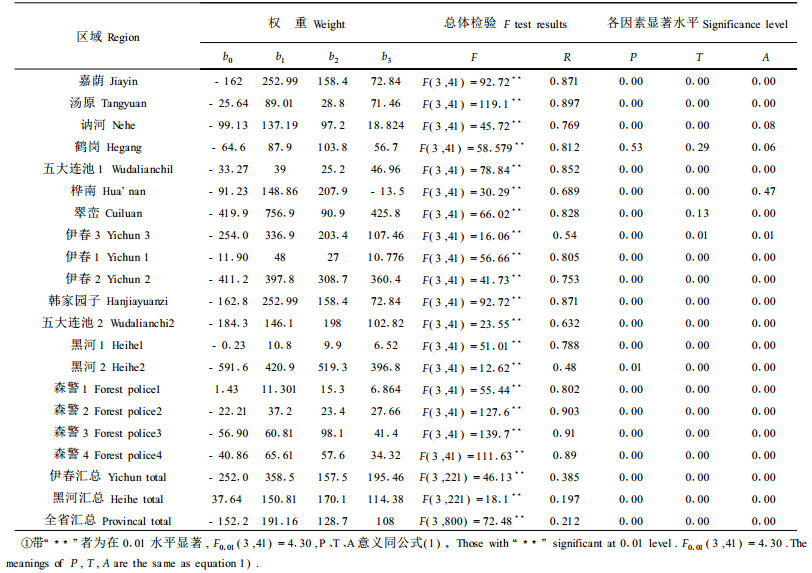
森林火灾初次派出人员数量与火场情况，如：火场面积(P)、到达火场所需时间(T)、火场风力等级(A)之间的多元线性回归结果列于表 2。为了各因子权重之间具有可比性，3个因子都进行了最大值归一化，转换成[0，1]之间的数值，其中风力级数最大值为3，到达火场所需时间最大值为90 min，火场面积最大值是2 hm²。

对18个县级单位、黑河、伊春两地区及全省汇总的数据而言，初次派出人员数量与上述3个因子的回归总体都显著，除翠峦和桦南1个火场变量与派出人员数量回归不显著外，其它区域的3个火场变量与派出人员数量之间回归全部显著，表明3个火场变量对派出人员数量影响的线性关系。因此，建立的根据火场情景模拟初次派出人员数量的模型(模型1)如下：

(1)

其中：N：初次派出的人数；P:归一化火场风力等级；T：归一化到达火场所需的时间；A：归一化火场初始面积：b₁、b₂、b₃为回归权重，b₀为多元回归截距，数值见表 2。

如果将模型(1)中的b₀看作是基本派出人员数量，将各因子的权重看作是单位因子变化时所需增加的人力，则b₀为正值似乎更合理，但本文b₀多为负值，表明指挥员头脑中对多因子响应的规则不仅有线性累积，还可能存在乘法关系或其它非线性的规则。为此，需要对模型形式进行修正。

表 2表明，派出人员数量与3个火场变量具有良好的线性关系，说明每个变量对派出人员数量都有影响，总的效果可能是三个分量乘积的关系。为此，对这3个变量与派兵数量N分别进行线性回归，构造出3个中间变量y₁、y₁、y₃，y_i=c_i1x_i+c_i0，i=1, 2, 3, x₁、x₂、x₃分别是归一化的火场风力等级、到达火场所需的时间和火场初始面积，c_i1、c_i0为回归系数。y₁、y₁、y₃可看作是3个变量单独作用时的派出人员数量。令y_t=y₁y₁y₃，则y_t表示3个火场状态变量的乘积作用，若问卷中存在乘积关系；y_t应与N具有良好的相关性，其相关系数要比式1)大。

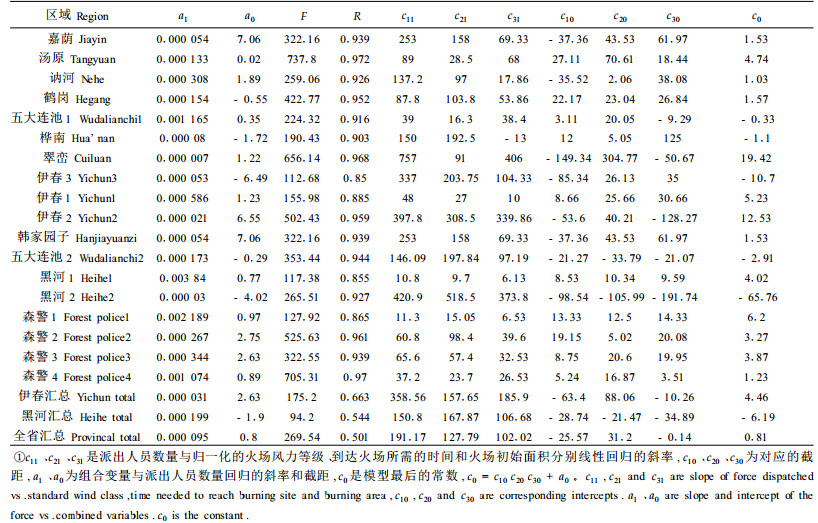
对派出人员数量N和y_t进行线性回归，所得回归系数a₁、a₀和相关系数R及其F统计检验结果列于表 3。该F值远远大于F_0.01(1，43)=7.28，回归结果都极其显著。式1)的相关系数均值为0.709，y_t与N的相关系数均值为0.875，差异显著性t检验值为2.941＞t_0.01(40)=2.704，差异极显著，表明N和y_t的相关系数明显好于式1)构造的变量与N之间的相关系数，或言之，从决定系数R²的角度看，变量y_t将更好地模拟N的变化情况。因此，我们得到了新的非线性派出人员模型，模型(2)：

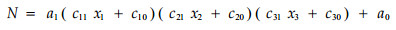
(2)

式中所有符号意义同前。

模型中c_i1x₁+c_i0, i=1, 2, 3，可以看成是各变量对派出人员数量影响的分量，其中斜率或变量权重c_i1, i=1, 2, 3，全部大于零。c_i0，i=1, 2, 3，部分小于零，在18个县级模型中，9个模型的全部系数都大于零，其余9个模型的部分截距小于零。(2)式展开后的常数c₀(c₀=c₁₀c₂₀c₃₀+a₀)在21个模型中只有6个小于零，这说明式2)比式(1)无论是在模型的理论结构描述还是在模拟的准确性方面都有所提高。负截距c产生的原因在于原数据中的非线性成分，但其所对应的斜率都很大，只要变量值超过一个很小的阈值就能保证派出人员数量为正，这在实际中是能够满足的。

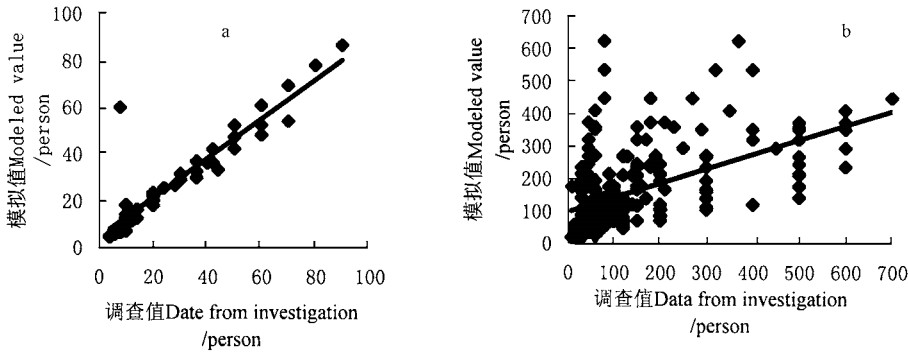
18个县级模型除黑河2外，相关系数都很高高，模拟误差小，模拟派出人员数量和实际值之间的关系基本如图 1a所示。而汇总模型如全省模型、伊春和黑河两地区模型类模型的模拟值与实际值差别较大，其模拟派出人员数量和实际值之间的关系见图 1b。这说明以县级为单位或单个问卷数据为基础建立的派出人员模型准确度高，而基于多地区或多问卷数据建立的模型模拟能力很低。这反映了决策水平的地区或个人间的差异。在今后的林火扑救辅助决策研究中，应根据各地情况分别建立模型，而不是多个县合在一起。

2.3 对影响派出人员决策因素的分析 2.3.1 火场情景因子对初次派兵数量的影响

模型中c_i1x_i+c_i0, i=1, 2，3，可以看成是各变量对派出人员数量影响的分量，而且这些分量对派出人员数量的影响是独立的。因此，分析变量斜率或权重可以分析各指挥员对相应变量的重视程度。表 3显示，对研究地区的大多数指挥员而言，风速、到达火场所需时间、火场面积确实是影响派出人员数量的因素，不同指挥员之间的权重差别很大，对同样的火情，有的指挥员要派出数百人，而有的指挥员只派出数十人。这体现了不同指挥员决策水平的差异，也可能是各地扑火设施差异造成的。但总的来说，森警部队派出的人数较少，这在一定程度上反映了他们与地方专业队扑火战术的差异。

根据表 3中各变量的权重统计，67%的指挥员将火场风力看作影响派出人员决策的首要因素，33%的指挥员将其看成是第二重要因素。22%的指挥员将到达火场所需时间看作影响派出人员决策的首要因素，39%的指挥员将其看成是第二重要因素，其余39%的指挥员将其看作最不重要的因素。只有11%的指挥员将火场面积看成是首要因素，28%的将其看作是第二重要因素，61%的将其看作最不重要因素。火场面积对派出人员数量应该有较大影响，在这里不重要是因为给定的火场面积都比较小。因此，在火场面积不超过2 hm²时，这三个因子按对派出人员数量的影响程度的降序排列是：风速、到达火场所需时间、火场面积。

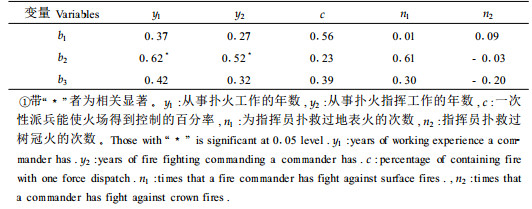
2.3.2 指挥员工作背景对各权重的影响

从表 4知，只有工作年数和从事指挥工作的年数与到达火场所需时间的权重呈正相关，这说明，工作时间越长、扑火经验越丰富，赋予到达火场所需时间的权重越大，对到达火场所需时间越重视。其它背景因素对扑火决策没有统一的影响。

3 结论

风速、到达火场所需时间、火场面积对初次派出人员数量有显著影响。本文利用两次线性回归建立的非线性模型可较好地模拟根据这3个因素确定的森林火灾扑救中初次派出人员数量。从而也说明扑火指挥人员对3个变量中的每个变量而言，其决策过程是线性的，但最后的决策是将这些分量以乘积的形式统筹考虑。

根据各地情况分别建立的模型模拟效果好，而以地区或省为单位进行模拟效果不好。

在火场面积较小时，多数人(67%)将风力看作是影响初次派出人员数量的首要因素，其次是到达火场所需时间，再次是火场面积。赋予到火场时间的权重与从事森林防火工作的时间正相关。

4 讨论

本文模拟的初次派出人员数量是扑火指挥员个人头脑中的最佳决策，不一定是在已知条件下的最优扑火方案，在实际扑火中未必每次都能将森林火灾扑灭。这与温广玉等(1995)建立的扑火人数经验公式不同。后者的公式可在火场面积、风速、防火期时段、扑火用时、扑火起时5个变量己知的条件下提供不是最佳但肯定能将火灾扑灭的人数。但下面两个方面制约了该公式在辅助决策中的应用：(1)在实际决策中总是要使用最少时间将火灾扑灭，但最少时间有下限，公式对此没有约束。(2)该公式是根据火场因素和总扑火人数建立的，该人数在扑救过程中可能是多次派出人员的结果。本文模型的意义就在于在非优化的辅助决策中可以直接应用，可以直接加入到现有的计算机辅助决策系统中。

模型误差除来自对非线性决策过程的近似外，与影响因素不全。本文只考虑了风速、到达火场所需时间、火场面积3个因素，对其它因素没有考虑。不同地区的扑火设施、条件对派出人员数量会有所影响。尽管在问卷中对扑火过程的一些变量进行了统一假设，但每个指挥员在填写问卷时，仍然会受本地特殊的扑火情况或因素影响。同时与答卷人回答问题的客观态度、负责态度等有关。

指挥员的工作经验对扑火决策应该有相当的影响，在这里工作经验只对到达火场所需时间权重有影响，对其余两个因子没有影响。即使工作背景对火场面积权重有影响，也可能由于问卷中火场面积较小而没有体现出来，将来应在问卷中适当加大火场面积。对风力而言，可能工作背景对风力权重的影响确实很小，或是各指挥员己给予了充分重视，不是放在首位就是第二位，从相关分析中体现不出来。在回收的问卷中，部分背景资料缺失，对研究结果也会产生一定影响。