1 Introduction

In many real engineering systems, the observation vector is often not available in its entirety to the controller(Borker et al., 1996; Caines et al., 1996; Cover et al., 1991), but a quantized version of it transmitted over a communication channel with accompanying transmission delays and distortion, subject to bit rate constraints. This problem has attracted some attention in recent years, see, e.g. (Delchamps, 1990).

The aim of this note is to study the impact of the communication constraints on properties of linear feedback control systems. The model studied here consists of a plant and a controller which locate far from each other. The observation of the plant is quantized, coded and transmitted to the remote controller via a communication channel with finite bandwidth. Once the coded observation is received by the controller, it is decoded and the feedback control is computed and decoded, and transmitted back to the plant. Obviously, the system can never be asymptotically stabilized if the uncontrolled dynamics is unstable due to the inherent delay in the feedback control caused by the finite communication capacity. So a new concept called containability is introduced by Wong and Brockett(1995).They also provided necessary conditions as well sufficient ones for systems to be containable. On the other hand, the concept of usual controllability is no longer meaningful in this case because the information about state of the system is quantized measurements instead of exact measurements. Instead, a weaker controllability concept, called set-controllability is introduced. Some necessary and sufficient conditions for systems to be set-controllable are derived in the note. The relationship between the containability and controllability will be addressed.

The note is organized as follows. Section 2 formulates control problems with communication constraints for linear systems. In Section 3, some definitions are introduced, and some sufficient conditions for systems to be controllable are derived. The conclusion is given in Section 4.

2 Control problem with communication constraints

Consider a continuous-time system with linear dynamics:

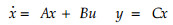
(1)

where x ∈Rⁿ, u ∈R^m, and y ∈R^r, A, B and C are matrices with appropriate dimensions.

The observation of x(t), y(t) is transmitted to a remote decision-maker for computing the appropriate level of feedback control. For simplicity, assume that it takes δ=1/R second to send one bit from the plant to the controller and visa versa from the controller to the plant, where R is the transmission rate in bits per second. Hence, if a bit is sent at time zero, it will be received at time δ at the receiver. Unlike classical models, the observed information is not transmitted continuously. Therefore, we assume that x(t) is sampled at time instants {r_i}_i=0^∞ with r₀=0; the other sample instants will be defined later.

Before an observation can be transmitted, it must be quantized and coded for the transmission. It is assumed that prefix codes are used so that the ending of a codeword is immediately recognizable(Cover et al., 1991).The quantization and coding function can be symbolically represented by a function H from the state space Rⁿ to D where D stands for the set of finite length strings of symbols from a D-ary symbol set. Therefore, the i-th transmitted codeword from the plant to the controller is c_i=H[y(r_i)].

Let l denote the codeword length function. Then the codeword is received by the controller at time s_i=r_i+l(c_i)δ. Once the coded observation is received, it is decoded and the feedback control is computed and coded for transmission back to the plant. Assume the Markovian feedback law(Wong et al., 1995)is used, that is, the i-th control codeword is d_i=g(c_i), where g is function from D to R^m. It is easily seen that the control codeword d_i reaches at the plant at time t_i=r_i+l(c_i)δ+l(d_i)δ. We assume an impulse control scheme is used in the sense that:

In summary, the Markovian Finite Communication Control (MFCC) model can be expressed by the following set of equations:

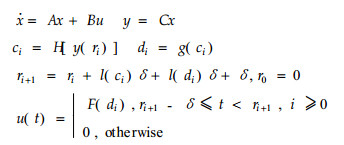
(2)

A MFCC system with unstable modes can not be made asymptotically stable since there is the delay between observation instants and control time(Wong et al., 1995). In this note, the study will be focused on a weaker controllability, namely set-controllability.

3 Definitions

For the system(2), the concept of controllability is no longer meaningful for lack of information of every point. Therefore, in what follows, we will introduce the notion of set-controllability for(2).

Definition 1 (Partition) (Caines et al., 1996) A finite analytic partition of the state space D⊂ Rⁿ of (2) is a pairwise disjoint collection of subsets π={x₁, x₂, L, x_nπ} such that each x_i is path-connected and of non-zero Lebesgue measure, and is such that

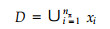
Moreover, if for all i=1, …, n_π, x_i is a rectangular cube whose edges are parallel to the coordinate axes and which has length Δ_i in the direction x_j, j=1, …, n, then the partition π is called a uniform partition (Delchamps et al., 1990), denoted as π_u. If Δ₁=…=Δ_n=Δ, Δ_n=1, then the partition π is called an equal uniform partition, denoted as π_u^e. If Δ₁=…=Δ_n=1, then the partition π is called a unit uniform partition, denoted as π_u^μ.

Definition 2   For a given partition π, a bounded path-connected set M with non-aero Lebesgue measure is said to be controllable by one step to another bounded path-connected set N, also with non-zero Lebesgue measure, if for any non-empty set M_j ∈M_π there exists a corresponding coded feedback control u_j such that all the points started in M_j enters N at the sampling instant r=[l(c_j)+l(d_i)+1]δ where M_π={M∩x_i, i=1, …, n_π}.

Let q denote the number of non-empty sets in M_π, and M₁, …, M_q, the q non-empty sets in M_π.

Lemma 1 Assume that for all j=1, …, q, there exist a point x_j∈M_j and an input u_j such that

and

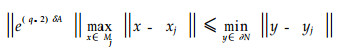
with ∂ N the boundary of N. Then M is controllable by one step to N.

Proof: All the points observed in M_i are coded with the codeword c_i with length i, and the feedback control, u_i, corresponding to the codeword c_i is coded by the codeword e_i with length q-i+1. It follows that r=q+2. For brevity and convenience, such a coded feedback is referred as to standard coded feedback.

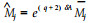
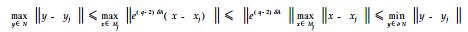
Let , Then according to relation

(3)

It is easily seen that all the points started in M_j enters in N at r=q+2 for all j, which implies that. M is controllable by one step to N.

For the case that the system is controllable, the following corollary can be easily obtained.

Corollary 1 Assume that the system (1) is controllable. Then

For a given uniform partition π_u, M is controllable by one step to N if

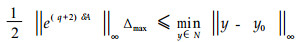
with y₀∈N and Δ_max=max{Δ_i, i=1, l, n};

For a given equal uniform partition π_u^e, M is controllable by one step to N if

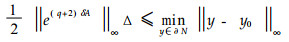
For a given unit uniform partition π_u^u, M is controllable by one step to N if

Proof: Since the system is controllable, it follows that there exists u_j such that the center of M_j can be steered to y₀ for all 1≤j≤q. The results can be easily verified by using Lemma 1.

From Corollary 1, the following results can be easily proved.

Corollary 2 Assume that the system (1) is controllable. Then

For a given uniform partition π_u, M is controllable by one step to a cube O with the length of side r_o if

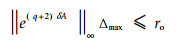
For a given equal uniform partition π_u^e, M is controllable by one step to a cube O with the length of side r_o if

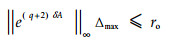
For a given unit uniform partition π_u^u, M is controllable by one step to a cube O with the length of side r_o if

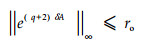
If A is in a triangular form with maximal eigenvalue λ_max, it is possible to prove the following theorem which provides sufficient and necessary conditions for a set, containing at least one set of π_e^u or π_u^u, to be controllable to a cube by one step and by using standard coded feedback.

Theorem 1 Assume that A is in a triangular form with maximal eigenvalue λ_max, B and C are nonsingular and O is a cube with the length of side r_o, and consider the standard coded feedback. Then

For a given equal uniform partition π_e^u, a set M, which contains at least one set of π_u^e, is controllable by one step to O if and only if

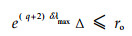
For a given unit uniform partition π_u^u, a set M, which contains at least one set of π_u^u, is controllable by one step to O if and only if

Proof: The sufficiency is the straightforward consequence of Corollary 2. Now let us prove its necessity. If

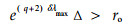
then for X⊂ M⌒π_u^e (there always exists such an X since M contains at least one set of π_e^u), it is easily seen that there are at least some points of the image e^(q+2)δAX whose coordinate values in the direction associated with λ_max are larger than r_o. As a consequence, M can not be controllable by one step to O.

Note that some sets which can not be controlled by one step to a certain set may be controlled by several steps to the set. The following example is the case.

Example 1 Consider the system

Now assume that δ=0.009 and Δ=Δ₁=Δ₂=1. Consider the sets M and N depicted, It is easily seen that

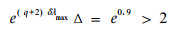
which means that M can not be controlled by one step to N. Fortunately, a straightforward calculation shows that M can be controlled by one step to a rectangular, say L, whose sides have lengths of 3 and 2. Due to

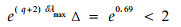
(4)

it follows from Corollary L is controllable by one step to N. So we may say M is controllable by two steps to N.

Definition 3 For a given partition π, a bounded path-connected set M with non-zero Lebesgue measure is said to be controllable by p steps to another bounded path-connected set N, also with non-zero Lebesgue measure, if there exist p sets, say M₁, …, M_p, such that M_i is controllable by one step to M_i+1 for all 0≤i≤p+1 with M₀=M and M_p+1=N.

Theorem 2 Consider the following system:

(5)

with a_i>0, b_i and c_i non-zero, i=1, …, n. Consider a unit uniform partition π_u^u. Assume that M={x∈Rⁿ:α_i≤x_i≤β_i, i=1, …, n} with β_i≥α_i+1 for all 1≤i≤n, and N={x∈Rⁿ:γ_i≤x_i≤μ_i, i=1, …, n}. Then M is controllable by p steps to N if

(6)

and for all 1≤i≤n,

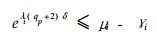
(7)

with q₁=∏_i=1ⁿ[β_i-α_i], where [α] denotes the smallest integer larger than α.

Proof: Without loss of generality, assume that α₁=α₂=…=α_n=0. It is obvious that there are q₁ cubes in π_u^u which intersect with M. As a result, r=(q₁+2)δ. It is easily seen that each cube can be controlled by one step via a standard coded feedback to the set:

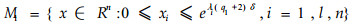
Similarly, there are 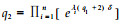cubes in π_u^u which intersect with M₁. Thus, each cube of these q₂ cubes can be steered by one step via a standard coded feedback to the set:

By induction, the set

can be driven by one step via a standard coded feedback to the set:

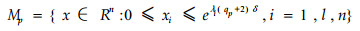
which is contained in N due to (6).

4 Conclusion

The problem of feedback control for a linear system with finite communication capacity is discussed. The concept of set-controllability is introduced, and sufficient and necessary conditions are provided for a system to be set-controllable.