生长方程作为描述一种有机体或一个种群大小随年龄变化的模型，可以反映某些生物生长的规律性(Zeide, 1993)。从数学角度讲，若一个方程中包含3个或更多自由参数，差不多任何曲线都可以逼近；很明显，若方程参数个数与观察数据点数目相等，则任何方程均可以通过所有数据点，这样，方程的灵活性虽达到理想状态，但同时方程也就失去了描述树木特定生长趋势的性能。而且，方程的参数个数不可能任意增加，实际上，方程的参数往往并不多，参数个数比较接近，那么方程间模拟精度的差异究竟是如何产生的呢?这里可以从林分及方程两个方面寻找原因，一般意义上，对于相同的方程而言，不同的林分数据拟合所得到的精度不尽相同，对于同一组林分数据，不同的方程模拟的精度亦会存在一定的差异，林分数据和方程表达形式的差异决定了方程模拟精度的高低。

人工林是指通过植树造林或通过苗木进行森林更新而建成的林分，这些林分或全部是外来树种造林，或是集约栽培经营的乡士树种造林，而且具有不超过2个树种、同龄和造林模式规范3个共同特征(FAO，1998)。人工林经营的目的就是要达到定向、速生、丰产、优质、稳定及高效(盛炜彤，1996)。为实现这一目的，国际上通常采用遗传控制、立地控制、密度控制等三大控制以及适度人为干扰(主要为间伐)和维持地力为主体的培育、经营措施，这些措施一定程度上决定了林分的生长发育进程和林分生长特征。因此，对于模拟的一方——林分而言，研究影响林分构成特征的这些措施对模拟精度的作用程度是林分直径结构模拟的重要课题，而以往在这方面的研究是很不够的。应用“S”型生长方程描述林分直径累积百分比分布正受到国内外学者的重视(惠刚盈等，1995；吴承祯等，1998；Von Gadow，1998；ISHIKAWA，1998)，并被证明是一种可靠而有效的方法。然而，就模拟的另一方——生长方程来说，理论生长方程在描述林分直径分布时所表现出精度高低的实质原因一直未能给出很好的解答。鉴于此，本文从理论生长方程曲线拐点的角度进行了探讨，期望能给出这一问题的满意回答。

1 材料与方法 1.1 试验区概况

试验区设置在江西省分宜县大岗山林区。大岗山区属罗霄山脉北端的武功山支脉，位于东经114°30′~114°45′，北纬27°30′~27°50′。气候温暖湿润，属亚热带季风湿润类型，年平均温度为15.8℃~17.7℃；7月平均最高温度28.8℃，日最高温度39.9℃；1月平均最低温度为-5.3℃，日最低温度-8.3℃。全年日照平均时间为1 657 h，最高为2 047 h，最低为1 378 h，日照百分率约为37%。太阳总辐射年平均为486.6 kJ·cm^-2。年平均蒸发量约为1 503 mm，最多为1 770.8 mm，最少为1 274 mm。年平均降水量为1 591 mm，最多为2 227.6 mm，最少为1 069.8 mm。年平均无霜期为265 d。本区属地带性低山丘陵红壤、黄壤类型及其亚类的分布区。

1.2 试验材料

材料来源于大岗山年珠林场、山下林场的固定试验地，具体试验设计及林分调查方法可参考童书振等(2002)有关杉木林分密度效应的研究报告及童书振关于杉木间伐中试林的定位研究¹⁾。本研究采用固定样地共计48块；年珠、山下两林场每块样地面积及采用林分年龄范围分别为600 m²、6~20 a和500 m²、9~27 a，样地初植密度分布范围为1 533~9 983株·hm^-2。每块样地均经多次观测，每一次观测均记为一个独立样本，总样本数为49 1个，其中立地指数为12、14、16、18的样本数分别有59、263、139、30个，间伐与未间伐的样本数分别为173、318个。按照2 cm的径阶距，将每一样本的直径序列划分径级，分别统计各径级的林木株数，从而得出林分径阶分布表。

1) 童书振.杉木间伐中试林定位研究.见：洪菊生等编.速生丰产林培育研究报告选编.北京：中国林业科学研究院世界银行贷款项目办公室(第四集)，1997：61-70

1.3 研究方法

本研究采用概率密度函数中运用最广的Weibull分布函数(Bailey，1973)及理论生长方程中的Gompertz(1825)、Mitscherlich(1919)、Logistic(Verhulst, 1838)、Richards(1959)和Korf(Kiviste, 1988)等6种不同的方程对林分直径累积分布进行模拟，各生长方程之基本形态详见表 1；采用剩余标准差(s)评价各生长方程的模拟精度；采用直观分析和图示法分别研究年龄、立地、密度及间伐强度等因子和生长方程对模拟精度的影响程度。

2 结果与分析 2.1 生长方程在不同年龄、立地、密度、干扰强度时模拟效果的评价

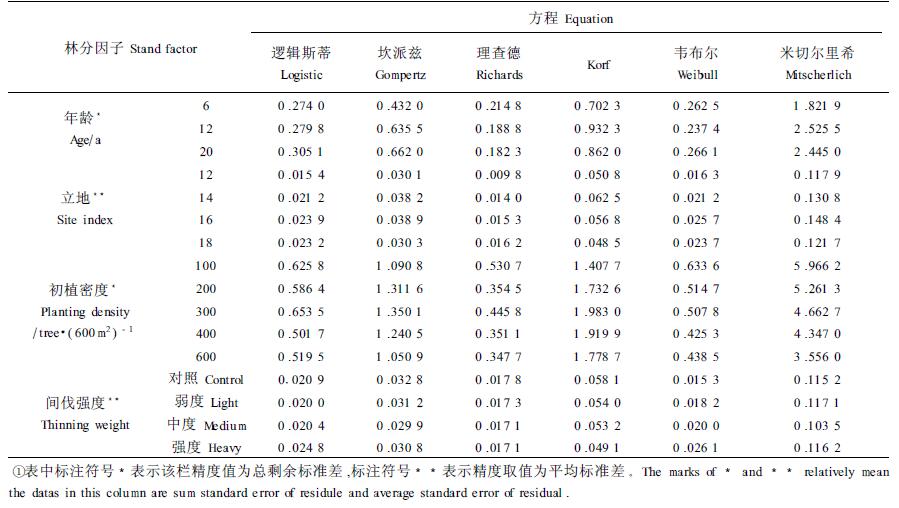
为评价不同林分状况及生长方程对模拟精度的影响强弱程度，本文按年龄、立地、密度以及间伐强度对林分依次进行了分类，并分别统计了各理论生长方程的模拟精度，详见表 2。其中，由于不同年龄间、不同密度间的林分个数相等，表中精度数据为总剩余标准差，不同立地、不同间伐强度时表中数据为平均剩余标准差。

为使统计数据更直观，作图 1。

从表 1、图 1可以看出，总体上，对于Richards等6个生长方程中的每一个方程而言，不同年龄、不同立地、不同初植密度以及不同间伐强度情形下，方程模拟精度均存在一定差异，这种差异是由于模拟对象即具体林分直径分布不一致所引起的，然而此种差异表现相当微弱；而当林分处于相同的各种状态时，不同生长方程间整体上模拟精度差异均十分明显。相对由不同生长方程所引起的模拟精度差异，林分自身所造成的模拟精度差异是微弱的。因此，就必须对生长方程造成模拟精度差异的实质原因作进一步的探讨。

2.2 生长方程模拟精度高低产生原因的探讨

对于理论生长方程来说，方程的拐点至关重要，且具有非常明确的生物学意义。一方面，拐点为生长方程曲线凹凸性状的分界点，决定着方程的形状：另一方面，树木的生长在理论上呈“S”型曲线，拐点处意味着连年生长的高峰期(盛炜彤，1996)，由分化所引起的林木径阶株数累积分布也呈现“S”型状态，拐点具体表示直径累积频率变化量最大时刻。在进行数据实际拟合时，生长方程曲线的拐点将对拟合的精度产生重要的影响。因此，研究不同生长方程模拟精度高低产生的原因时，方程的拐点差异就有条件成为探讨的突破点。

2.2.1 生长方程模拟精度的比较

表 3为Richards等6种生长方程模拟精度的比较结果。

由表 3可知，6种生长方程的总体精度大小依次为Richards、Logistic、Weibull、Gompertz、Korf及Mitscherlich。

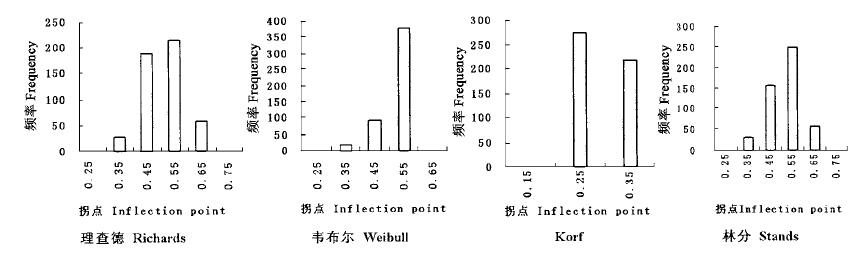
2.2.2 各生长方程的拐点分布情形

经过模拟发现各生长方程拐点分布情形如表 4所示。

对于单个林分而言，最优模拟方程能精确地反映林分的实际直径分布状况，故将最优模拟方程所描述的分布情况当作林分的理论分布情形，其拐点作为林分理论分布的拐点，为方便描述，简称林分拐点。可以看出林分直径累积分布曲线拐点存在一个范围，且有其主要分布区间——0.4~0.6，这一区间所占比例高达82.28%，这说明绝大多数样本实测值的拐点在0.4~0.6间出现；Richards、Korf及Weibull等3个生长方程最佳拟合曲线的拐点亦具有一个浮动范围，并非为定值，且均存在如上表所示的主要分布区间；Logistic和Gompertz方程拐点固定；Mitscherlich方程不存在拐点。

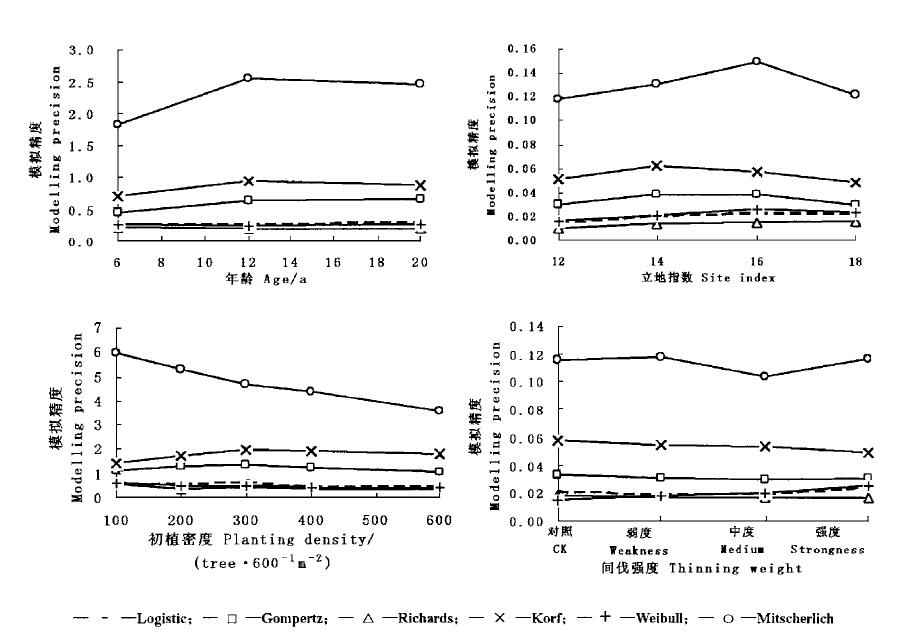
2.2.3 有无拐点方程间模拟精度的比较

表 3中所列6种生长方程除Mitscherlich式不存在拐点外，其它方程均存在拐点。统计可得，Richards、Logistic、Weibull、Gompertz、Korf等方程的模拟精度分别为Mitscherlich方程的74.7、36.2、33.4、12.9、5.5倍。因此可以得出结论：有拐点的生长方程较无拐点的生长方程之模拟精度要高。图 2描述了Richards、Korf、Mitscherlich等3个方程理论值与实测值吻合程度的典型情况。

从图 2可以直观地看到，实测的直径累积百分比分布曲线具有拐点，Richards与Korf两方程的模拟曲线也具有拐点，因而与实测值相当吻合，而Mitscherlich方程无拐点，致使其理论值与实测值相差较大，模拟精度也就较低。

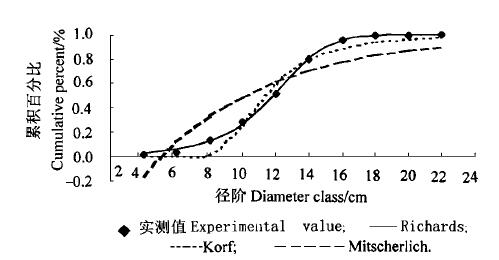
2.2.4 浮动拐点方程间模拟精度的比较

因为林分实测直径累积百分比曲线拐点具有一定变动范围，故模拟精度最高的生长方程应该是最佳拟合曲线拐点也具有一定变动范围的方程。Richards、Korf及Weibull等3个生长方程最佳拟合曲线的拐点均具有一个浮动范围，3方程与林分的拐点区间分布情况如图 3所示。

由图 2、3可以清晰地看到，Richards、Weibull及Korf等3个生长方程最佳拟合曲线拐点的范围依次减小，结合表 3显示的结果，能初步得出这样一个结论，即对于具有浮动拐点的生长方程而言，其最佳拟合曲线的拐点范围愈大，生长方程拟合的精度就愈高。拟合总体精度最高的Richards生长方程拐点范围与林分相同，而且，在0.4~0.6分布区间竟也出乎意料地完全相同，也为82.28%；Weibull方程以前被人们所认识主要是以其概率密度函数形式出现，因该方程在形状参数c＞1时具有拐点，故本文将其看作生长方程进行应用，该方程在0.4~0.6这一区间的拐点存在比例达95.93%，其拟合精度相当高；Korf方程最佳拟合曲线的拐点浮动范围在0.190 6~0.348 9之间，这一结果与李凤日¹⁾ 关于树木生长曲线(应用Korf方程时)的拐点出现在0~A/e(A为渐近值)之间的论点相一致，然而该方程模拟精度较Richards与Weibull均低很多，这主要是因为方程拐点浮动范围不在林分拐点的主要存在区间。为更好地解释这种现象，这里提出有效拐点区间的概念，即生长方程拐点与林分直径累积分布曲线拐点完全相同或十分接近的存在区域，有效拐点区间愈大，方程拐点的有效性就愈大。Richards方程拐点分布范围宽，主要分布区间也与林分拐点主要存在区间一致，其有效拐点区间大，故模拟精度高；Weibull方程拐点浮动范围略窄、分布在林分拐点主要存在区间的比重过大，其有效拐点区间略小，模拟精度也就较Richards略低；Korf方程拐点虽存在一个浮动范围，但过窄，且拐点均在林分拐点主要存在区间(0.4~0.6)之外，因此其有效拐点区间小，模拟精度也就较前两者低许多。

1) 李凤日.落叶松人工林林分生长与收获模型.北京林业大学，博士学位论文，1996

2.2.5 固定拐点方程间模拟精度的比较

本文所列“S”型生长方程中拐点固定的方程有Gompertz和Logistic，图 4描述了两方程在林分直径累积分布曲线拐点散点图中的位置。

值得注意的是，Logistic方程因其拐点固定，其拐点轨迹平行于x轴，拟合精度比较稳定，而且该方程拐点值(0.5)在前文所指出的林分拐点主要分布区间(0.4~0.6)之内，如图 4所示，处于这一区间的核心区域，所以该方程具有良好的拟合性能。Gompertz方程同理，但其拐点偏离了林分直径累积分布曲线拐点的主要存在区间，故精度要较Logistic方程为低。对于拐点固定的方程，可以将方程拐点处在林分拐点存在区间的位置以精确度进行衡量，精确度愈高，方程拟合精度愈高，如Logistic方程的拐点由于处在林分拐点主要存在区间的核心位置，因而拟合精度高。此种方程拐点的精确度亦可理解为方程拐点的有效性，精确度愈高，方程拐点有效性愈大。

2.2.6 拐点固定的方程与拐点浮动的方程间模拟精度的比较

6种理论生长方程中拐点固定的有Logistic和Gompertz，拐点浮动的为Richards、Korf及Weibull等3个方程，如前所述，此6种方程的总体精度由大到小依次为Richards、Logistic、Weibull、Gompertz、Korf及Mitscherlich。从精度大小的排序情况来看，不能说拐点浮动的方程模拟精度就比拐点固定的方程要高，反之，也行不通。可以发现，方程拐点落在林分直径累积分布曲线拐点主要分布区间的比重大时，方程模拟精度就高，如Richards、Logistic和Weibull；拐点落在林分直径累积分布曲线主要分布区间之外的方程模拟精度就要低一些，如Gompertz及Korf。据此，结合前面对方程在拐点固定与浮动两种情形下模拟精度的分析，可以认为，方程有效拐点区间愈大、拐点精确度愈高或有效性越大，其模拟精度愈高。Richards方程的有效拐点区间包含了拐点精确度高的Logistic方程的拐点，故模拟精度高，Weibull方程本亦同理，但因个别样地拟合时精度误差较大，且与Logistic方程精度非常相近，而导致较后者精度反而略低，此种情况亦属正常；Korf方程拐点虽存在一个浮动范围，但这一范围偏离了林分拐点的主要分布区间，又因其分布范围上限值要小于Gompertz方程的拐点值0.348 9＜0.367 9)，导致方程拐点有效性较Gompertz小，故模拟精度相对要低。

总之，理论生长方程最佳拟合曲线的有效拐点区间愈大、拐点精确度愈高，从而拐点有效性越大，则方程模拟精度越高。

3 结论

理论生长方程应用在林分直径结构领域的研究时，表现出了良好的模拟性能，但不同的理论生长方程其模拟精度又有高低之分，本文从模拟双方——林分和方程的角度对产生这一现象的原因进行了探讨，得出以下几点结论：

总的来说，年龄、立地、密度、间伐强度等因素对Richards等6种生长方程的模拟精度没有明显影响；相对由不同生长方程所引起的模拟精度的差异，林分自身所造成的模拟精度差异是微弱的，前者起主要作用。

杉木人工林林分直径累积分布曲线的拐点存在一个范围，且有其主要分布区间——0.4~0.6；生长方程拐点的取值情形与各方程模拟精度的大小密切相关，具有拐点的方程模拟精度明显高于无拐点的方程。

理论生长方程最佳拟合曲线的有效拐点区间愈大、拐点精确度愈高，从而拐点有效性越大，方程模拟精度越高。

从本文研究结果看，Richards、Weibull及Logistic等3个方程模拟效果突出，可为以后其它树种的人工林，抑或天然林林分直径结构模拟的研究提供参考。