文章信息
- 邵卓平, 江泽慧, 任海青.
- Shao Zhuoping, Jiang Zehui, Ren Haiqing.
- 线弹性断裂力学原理在木材中应用的特殊性与木材顺纹理断裂
- THE PARTICULARITY OF APPLICATION OF PRINCIPLES OF LINEAR-ELASTIC FRACTURE MECHANICS TO WOOD AND FRACTURE PARALLEL TO GRAIN
- 林业科学, 2002, 38(6): 110-115.
- Scientia Silvae Sinicae, 2002, 38(6): 110-115.
-
文章历史
- 收稿日期:2001-05-10
-
作者相关文章
2. 中国林业科学研究院木材工业研究所 北京 100091
2. Research Institute of Wood Industry, CAF Beijing 100091
自从Porter (1964)的首篇论文发表以来, 将断裂力学应用于木材强度的分析已得到深入发展, 各国学者在这方面做了大量的工作, 应用的领域也由木构件的安全性评价延伸至木材加工利用等诸多方面, 已有许多的实验方法被用来确定断裂力学的参数, 其中木材断裂韧性KIC是诸参数中最为重要的力学指标, 它表征木材抵抗张开型裂纹失稳扩展的能力, 对评价质量、安全设计、改造加工工艺都有重要的意义。但由于没有统一的标准, 不同测试方法所得的结果有时相差很大, 缺乏多种方法之间的比较研究。本文以人工林杉木和马尾松为对象, 对线弹性断裂力学原理在木材中应用的特殊性、木材顺纹断裂的性质以及木材断裂韧性KIC的测试方法进行了研究, 以便为木材断裂力学的推广应用和制定木材断裂韧性KIC的测试标准提供理论依据。
1 线弹性断裂力学的原理断裂力学是研究含裂纹(缺陷)构件断裂强度的一门学科。早在断裂力学出现之前, 英国数学力学家Sneddon等(1946)就从数学弹性力学出发, 证明了在裂纹尖端区应力场具有r-1/2阶的奇异性, 即当r→0时, 诸应力分量都无限增大。显然, 对含有裂纹缺陷的构件仍使用以应力为参量建立的传统强度条件:

|
(1) |
来作为判断构件是否安全的依据, 就失去了意义。
Irwin (1957)利用Westergard应力函数, 从研究弹性体裂纹尖端的应力分布出发, 阐明裂尖处应力场的一般形式如下:

|
(2) |
式中:a为裂纹尺寸; σ∞为远离裂尖处的工作应力; r、θ为以裂纹尖端为原点的极坐标; fij (θ)为方位函数, 并略去了r的高阶项。对于裂纹前端任一点(其坐标r、θ是确定值), 由公式(2)可以看出该点的应力完全由σ∞ (πa)1/2决定, Irwin称此为应力强度因子K。一般来说, 应力强度因子可以写成如下形式:

|
(3) |
式中:σ为裂纹位置上按无裂纹计算的工作应力(相当σ∞); Y为形状系数(与裂纹形状、位置等有关)。可以看出, 应力强度因子K是工作应力、裂纹尺寸和几何形状的函数, 当这些因素综合起来, 使K达到材料的临界值KC时, 裂纹就将失稳扩展。这样, 就建立起线弹性断裂力学中的一个基本判据:
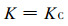
|
(4) |
裂纹按力学特征可分为三种类型:Ⅰ型(张开型)、Ⅱ型(滑开型)和Ⅲ型(撕开型) (见图 1), 相应的应力强度因子为KⅠ、KⅡ和KⅢ。实际裂纹体中的裂纹可能同时存在Ⅰ型和Ⅱ型(或Ⅲ型), 称为复合型裂纹。在三种基本类型裂纹体中, Ⅰ型裂纹是最常见和最危险的, 是工程断裂力学研究的重点。如果试样具有足够的厚度, 属平面应变状态, 则Ⅰ型裂纹发生失稳扩展时的临界应力强度因子的下限值KIC, 即是材料固有的性能, 它表征材料在线弹性范围内, 带裂纹工作时抵抗断裂的能力, 通常称为材料的平面应变断裂韧性或断裂韧度。因此, 求解裂纹体的应力强度因子和测定材料的断裂韧性是线弹性断裂力学中一项重要的工作。

|
图 1 裂纹力学特征 Fig. 1 Crack mechanics feature |
由于组织结构的原因, 木材属各向异性、非均匀材料, 气干木材在某种承载形式下其应力-应变曲线表现出线性特征, 符合线弹性行为, 且可近似视为正交各向异性材料, 其三个弹性对称平面分别垂直于木材的纵向(L)、径向(R)和弦向(T)。所以, 如果以第一个符号表示裂纹平面的法线方向, 第二个符号表示裂纹扩展的方向, 木材有六种基本的裂纹扩展形式, 分别为:TL、RL、LT、LR、TR、RT (见图 2)。
|
图 2 木材基本裂纹分类 Fig. 2 The six crack propgation systems of wood |
正交各向异性材料的断裂现象比各向同性材料要复杂得多。Sih (1968)应用复杂函数导出了正交各向异性材料裂纹尖端的应力和位移场方程式具有如下形式:
|
(5) |
式中:aij为材料的弹性常数; u1、u2、u3为材料的复合参数, 取决于材料各向异性的程度以及裂纹与纵向纤维之间的夹角α (图 3), Re表示取复函数fij的实部。分析比较上述方程, 就可发现正交各向异性材料断裂的复杂程度及其与各向同性材料断裂的重大差别。主要差别在于: (1)一般来说, 在含裂纹的正交各向异性材料中, 裂纹并不沿着初始的方向扩展, 而是常沿着纤维方向扩展。而线弹性断裂力学预先假定, 裂纹总是沿初始裂纹方向扩展; (2)即使在简单形式的载荷下, 正交各向异性材料中裂纹尖端也会有复合形式的位移, 这也与按Ⅰ、Ⅱ、Ⅲ型区分形式为基础的线弹性断裂力学原理不同; (3)正交各向异性材料裂纹尖端的应力场是材料复合参数的函数, 而这些参数又是材料性质以及裂纹与纤维方向夹角α的函数。这也不同于根据裂尖应力场分布与材料性质及方向无关而发展起来的线弹性断裂力学原理。

|
图 3 裂纹及纤维方向示意图 Fig. 3 Crack orientation α for fiber |
考虑到上述三个事实, 一般来说, 线弹性断裂力学原理对于正交各向异性材料是不适用的, 因为找不到三个材料常数KⅠC、KⅡC和KⅢC来表示正交各向异性材料的断裂韧性, 除非分别考察裂纹和纤维方向为任意固定夹角时的每一种情况, 并检验其对每种单独情况下的适用性, 这在实用上极不方便甚至不可能。然而, 如果初始裂纹沿纤维方向时, 正交各向异性主轴线分别与裂纹面方向和裂纹扩展方向重合, 在这一特殊情况下, 就消除了与上面阐述的线弹性断裂力学原理的所有偏离, 因为许多实验都证实: (1)裂纹沿初始方向扩展, 该方向与纤维方向一致; (2)位移不再是混合型的; (3)对于固定的裂纹与纤维的方向(α=0), 材料的复合参数就是常数, 因此裂纹尖端的应力分布仅是r、θ的函数。
上述三种情形表明, 线弹性断裂力学原理对裂纹沿纤维方向的情况是适用的。木材在树木生长过程和加工过程中形成的大多数裂纹和缺陷大都在纤维方向上, 而木材又在沿纤维方向上抵抗裂纹扩展的阻力最小。实验中的TL裂纹扩展与木材的径裂、RL裂纹扩展与木材的轮裂非常相似, 因此, 基于各向同性材料的线弹性断裂力学原理对木材裂纹顺纹扩展是适用的, 研究并测定表征木材抵抗顺纹开裂的韧性, 对木结构设计和优化加工工艺都有着重要的实用价值。
3 木材顺纹断裂韧性KIC的测试方法与结果目前国内外都有测定材料KIC的试验标准。例如:美国材料试验学会的ASTM-E399, 英国材料标准学会的BS5447-1977, 中国国家标准GB4161-84。试验所采用的试样有紧凑拉伸(CT)试样、三点弯曲(SEB)试样、拉伸(TS)试样和双悬臂梁(DCB)等(见图 4), 以及上述试样的改进形式。
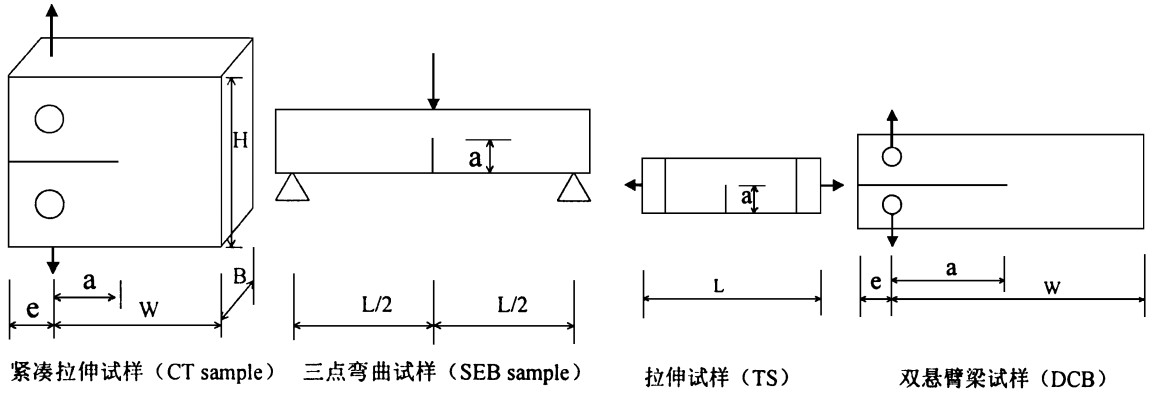
|
图 4 测试断裂韧性的基本试样 Fig. 4 The basic samples of testing for fracture toughness |
从理论上讲, KIC是材料本身的性能, 在一定的条件下, 它和加载方式、试样类型及尺寸无关。但从木材KIC测试的角度来看, 紧凑拉伸法(CT)简单易行, 试样尺寸小, 对小径级材尤为合适; 三点弯曲试样(SEB)常用于测定横纹断裂韧性, 制作含顺纹裂纹体试样需试材径级较大; 拉伸法(TS)的试样在制作时需要贴小片, 并对加载的拉伸夹头要求高; 采用DCB试样的柔度法是一种基于能量原理的实验标定方法, 精度较好, 但实验要求高, 工作量大。
为了验证木材的断裂韧性是材料的固有属性, 并不受试样形状和尺寸大小的影响, 本研究对含TL裂纹的杉木和马尾松木材试样抵抗顺纹开裂能力的断裂韧性作了测试, 考虑到试材的径级、试样制作的难易和此类裂纹体常遇的受载方式, 分别采用了CT、DCB试样和CT改进型WOL试样。试验用材采自中国林科院亚热带林研究中心下属林场。树龄25 a, 树高16 m, 杉木胸径26 mm左右、马尾松胸径23 mm左右。先锯解成中心板, 气干1 a, 平均含水率14%。试验在INSTRON电液伺服万能力学试验机上进行, 实验室温度约20℃, 相对湿度约65%。
3.1 不同厚度下CT试样的KICTL木材的紧凑拉伸试件是参照国标GB4161-84制作, 试样尺寸W=50、e=12.5、a=25、H=30 mm。Brrent (1976)用四点弯曲试样测定了南美松的断裂韧性, 并认为在试样厚度 > 5 mm时, KIC是一个常数; Boatright等(1983)也认为试件厚度在 > 10 mm后, 厚度对KIC无显著影响。为证实这一点, 考虑到本试材年轮较宽, 分别取厚度B=10、15、20、25、35、45 mm, 每组4~6件, 杉木、马尾松各31件。裂纹制作先锯一长槽口, 再用锋利刀片切割2 mm, 制成总长为a的尖锐裂纹。材料的断裂韧性计算公式如下:

|
(6) |
式中:PQ为临界载荷(下同);

|
本次实验结果表明, 含顺纹理裂纹的气干木材试件在张力作用下发生脆性断裂, 其载荷-裂纹张开位移(P-V)曲线均属第Ⅲ类曲线(按照我国或美、英等国的材料试验标准规定, 第Ⅰ类曲线指延性断裂曲线, 第Ⅲ类曲线指脆性断裂曲线), 因而实验所测得的Pmax即为临界载荷PQ (崔振源, 1981; GB4161-84)。将试件尺寸和PQ值代入公式(6)即可得到试件的断裂韧性值。杉木和马尾松CT试样的KIC值关于厚度的散点图见图 5、6, 对应某一厚度试样, 因木材材质变异的影响, KICTL值有较大的差异, 但从测试结果的总体来看(表 1), 两种材料的变异系数均小于20%、准确指数均小于5%, 表明使用CT试样测得杉木和马尾松断裂韧性的平均值分别为4.812和9.667 Nmm-3/2的实验结果是有效的, 同时也表明在厚度 > 10mm时木材顺纹断裂韧性受试样厚度的影响不大。这一结论与Brrent、Boatright等人的观点一致。

|
图 5 杉木(a)、马尾松(b) CT试样KICTL关于厚度B的散点图 Fig. 5 KICTL vs.thick B for CT samples of Chinese fir (a) and Masson pine (b). |
|
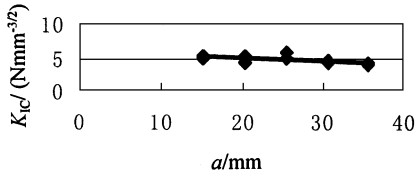
图 6 杉木WOL试样KIC关于裂纹长度a的散点图 Fig. 6 KICTL vs. length a of crack for WOL sample of Chinese fir |
|
|
WOL试件是紧凑拉伸试样的改进型, 它比标准CT试样稍长, 因而可以通过由不同的裂纹长度a来测定材料的值。WOL试件尺寸为:B=20 mm, W=2.55B, H=2.48B, e=0.13 mm。为了检验裂纹长度对杉木顺纹断裂韧性是否有影响, a取不同的裂纹长度, 使a/W分别为0.3、0.4、0.5、0.6、0.7, 共11个试件。试样制作与试验程序同紧凑拉伸试件的制作要求完全一致。断裂韧性计算公式如下:
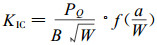
|
(7) |
式中:f (a/W) =30.96 (a/W) 1/2-195.8 (a/W) 3/2+730.6 (a/W) 5/2-1186.3 (a/W) 7/2+754.6 (a/W) 9/2
试验结果列于表 1中, 杉木WOL试样的KICTL平均值为4.689 Nmm-3/2, 与用CT试样所测的值接近, 其变异系数小于20%、准确指数小5%, 即说明测试结果的有效性, 同时也表明a/W在0.3~0.7范围内, 裂纹长度对木材顺纹断裂韧性无显著的影响。
3.3 基于能量原理的柔度法测定DCB试样的KICTL前面由CT、WOL试样测定木材顺纹断裂韧性, 都是基于把木材作为正交各向异性材料且裂纹沿纤维方向时其应力强度因子与各材料常数无关的假定之上, 采用各向同性材料断裂力学的计算公式得到的。但木材作为高度变异的生物材料, 其裂纹扩展受到裂尖处材料变异程度的影响, 因此, 上述假定是否成立、其计算结果是否就是木材抵抗顺纹扩展的断裂韧性, 需要做进一步验证。
Sih等(1965)研究了正交各向异性体单一裂纹尖端附近的应力场, 指出当裂纹与其上一对称平面平行时, 因弹性常数S16=S26=0, 而得到只含有四个独立弹性常数的能量释放率与应力强度因子的关系式:

|
(8) |
式中:S*为材料复合弹性常数, 由电测法测得, 再应用irwin-Kies关系式:

|
(9) |
即可在实验室里通过测定因裂纹扩展而引起的弹性裂纹体柔度的变化率, 计得临界应力强度因子即断裂韧性KIC值。
柔度法是一种基于能量原理的实验标定方法, 适合各种材料和各种试样形状。由于“耗散”在断裂区的能量来自试样的弹性主体, 所以, 裂尖处的应力状态及局部材料的变异将较小地影响弹性主体的能量变化, 从而使柔度法具有较高的精度。Triboulot等(1983)曾应用有限元法对含TL和RL裂纹的DCB试样进行理论计算, 证实试验中的柔度曲线与有限元素结果比较吻和。为此, 邵卓平等(2001)应用柔度法对杉木试材的KICTL值进行了测试, 试样采用双悬臂梁(DCB), 尺寸为W=300、e=20、B=25、H=80mm, 裂纹长度a分别取30、60、90、120、150、180、210、240 mm, 共8个试样。测定结果也列于表 1中, 显然, 杉木的三个实验值非常接近。
柔度法步骤如下:绘出对应不同裂纹长度试样的载荷一位移(P-V)曲线; 计算相应试件的柔度Ci (即直线段斜率的倒数); 选用指数函数进行拟合得到柔度的解析表达式C=0.6267exp (4.952a/W); 再由式(8)、(9)即可计得试件的KIC值。
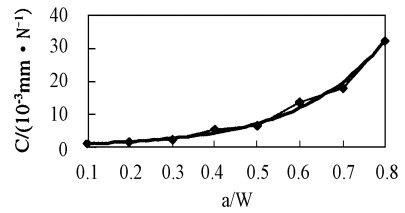
|
图 7 杉木DCB试样的柔度标定曲线 Fig. 7 Compliance plot curve vs. a/W for DCB sample of Chinese fir |
从方法上讲, 紧凑拉伸试样(CT、WOL)的KICTL值, 是参照GB4161-84测定; DCB试样的KIC值, 是基于能量原理的柔度法测定。前者试件用材少、易加工, 实验中只需测得试件在破坏时的载荷即可, 简便易行, 并且已有成熟的实验标准可以借鉴; 后者则是一种对各种材料都适用的方法, 普适可靠, 但因需先测定木材在三个主方向的弹性系数, 实验要求高, 工作量大。为了增大柔度的测定量值以提高精度, DCB试样尺寸常设计得较大。关于试样的平面应变条件, Triboulot等(1983)证明试样约在65%以上的厚度范围内满足平面应变条件, 因此, 平面应变的假设可以认为是成立的。
表 1给出了杉木CT、WOL、DCB三组试样断裂韧性测定结果的统计描述, 可见三者的平均值十分接近, 最大误差 < 0.136 Nmm-3/2, 最大相对误差 < 2.8%, 并且这三种方式的变异系数均小于20%, 准确指数均小5%, 表明三种实验方法的测定结果都是有效的。表 2给出三组样本值的方差分析, 进一步说明实验方法及试样对测定的KIC值无显著影响, 证明木材的顺纹断裂韧性的确是材料的一种固有属性, 在一定的条件下, 它和加载方式、试样类型及尺寸无关。由于CT试样对设备要求不高, 可直接以Pmax作为临界荷载PQ, 且试件耗材少, 可通过增大试件数量以满足断裂韧性的平均值在给定范围的有效性, 因此, 我们认为使用CT试样测定木材顺纹开裂的断裂韧性是可行和值得推荐的。
|
|
线弹性断裂力学原理对木材裂纹沿纤维方向的情况是适用的。当裂纹沿纤维方向且载荷对称地作用在裂纹面上时, 木材的顺纹断裂韧性的测试可以应用各向同性材料断裂力学的理论与方法来完成。
本实验表明木材的顺纹断裂韧性是材料的基本性质, 它与测试方法、裂纹体的几何形状、尺寸无显著影响。为保证满足平面应变状态和测定值的稳定性并考虑到木材年轮宽度, 试件厚度推荐值为20~30 mm。
顺纹理裂纹的木材断裂韧性的测定可选用紧凑拉伸试样(CT、WOL)或柔度法的DCB试样。由于CT试样相对简单易操作、设备要求不高、试件耗材少, 并可通过增大试件数量以满足均值在给定范围的有效性, 建议推荐使用CT试样。
本次实验测定的木材顺纹断裂韧性结果为:杉木KICTL=4.80 Nmm-3/2, 马尾松KICTL=9.667 Nmm-3/2。
崔振源编著. 断裂韧性与测试原理和方法, 上海: 科学技术出版社, 1981, 15~ 34
|
国家标准局. 金属材料平面应变断裂韧度KIC试验方法(GB4161-84). 北京: 中国标准出版社, 1984 http://www.csres.com/detail/107667.html
|
邵卓平, 任海青, 江泽慧. 2001. 柔度法标定木材断裂韧性的研究. 林业科学, 38(2): 113-117. |
Barrent J D. 1976. Effect of crack-front width on fracture toughness of Doouglas-fir. Eng. Frac. Mech., 8(4): 711-717. DOI:10.1016/0013-7944(76)90044-8 |
Boatright S W J, Garrentt G G. 1983. The effect of microstructure and stress state on the fracture behaviour of wood. J. of Materials Sci., 18: 2181-2199. DOI:10.1007/BF00555013 |
Irwin G R. 1957. Analysis of stresses and strain near the end of a crack traversing a plate, J. J. Appl. Mech., 24: 361-364. |
Porter A W. 1964. On the mechanics of fracture in wood. Forest Products journal, 14(8): 325-316. |
Sih G C, Prais P C, Irwin G R. 1965. On cracks in rectilinearly anisotropic bodies using singular isoparametric elements. Int. J. of Fracture Mech., 1: 189-203. |
Sneddon I N, Elliott H. A. Quart, Appl Math, 1946, 4: 229
|
Triboulot P, Jodin P, Pluvinage G. 1984. Validity of fracture mechanics concepts applied to wood by finite element calculation. Wood Sci Techol, 18: 51-58. DOI:10.1007/BF00632130 |
 2002, Vol. 38
2002, Vol. 38


