文章信息
- 顾继友, 高振华, 王逢瑚, 李治国, 程瑞香.
- Gu Jiyou, Gao Zhenhua, Wang Fenghu, Li Zhiguo, Cheng Ruixiang.
- 刨花板厚度方向变形研究Ⅲ.刨花板厚度方向变形模型及规律的确定
- STUDIES OF THICKNESS SWELLING ON WOOD COMPOSITE Ⅲ.ESTABLISHMENT OF EQUATIONS FOR DEFORMATION IN THE THICKNESS OF PARTICLEBOARD
- 林业科学, 2002, 38(4): 134-140.
- Scientia Silvae Sinicae, 2002, 38(4): 134-140.
-
文章历史
- 收稿日期:2000-01-11
-
作者相关文章
笔者曾提出刨花板厚度方向变形的模型:TS(t)= F (t)+ f (M.C, t)+ V (t)+ A(M.C, t), 并对其各项进行释因(顾继友等, 2002b), 但未给出模型及模型中各项的数学形式。对刨花板尺寸稳定性以定性的描述, 在实践中, 希望进行定量描述及直观地反映板的稳定性, 由此科学地指导生产, 制得性能优异的刨花板。
本研究是应用大量的数据点, 通过数学处理, 揭示刨花板厚度方向变形模型的具体数学形式及其各组成项的定性数学式。
1 实验材料及方法 1.1 实验材料大青杨(Populus ussuriensis, 绝干密度:0.359 g·cm-3), 购于哈尔滨木材市场。
兴安落叶松(Larix gmelini, 绝干密度:0.571 g·cm-3), 购于哈尔滨木材市场。
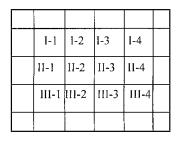
异氰酸酯杨木刨花板试件, 25 mm×25 mm×12 mm, 刨花用所购木材自制, 异氰酸酯胶粘剂自制, 热压条件:温度150 ℃, 时间3.5 min, 压力3.5 MPa, 施胶量5.0 %, 含水率12.8 %, 板放置15 d后锯割, 锯割图如图 1所示。
|
图 1 刨花板试件切割图 Fig. 1 The sample cutting for particleboard 试件Ⅰ - 2、Ⅱ -1、Ⅱ - 4、Ⅲ - 3用于测含水率及密度; 试件Ⅰ- 1、Ⅰ - 4、Ⅱ - 2、Ⅱ- 4、Ⅲ -1、Ⅲ - 4用于测吸水厚度膨胀率。 The samples of Ⅰ - 2, Ⅱ -1, Ⅱ - 4 and Ⅲ - 3 used for testing density and moisture content, the samples of Ⅰ - 1, Ⅰ - 4, Ⅱ - 2, Ⅱ - 4, Ⅲ -1 and Ⅲ - 4 used for testing TS. |
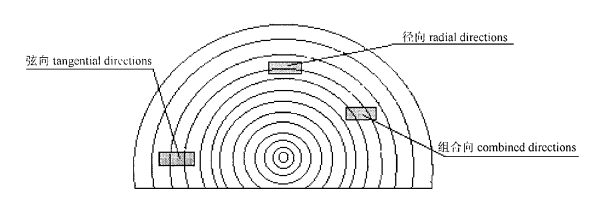
异氰酸酯落叶松刨花板试件, 25 mm ×25 mm ×12 mm, 刨花用所购木材自制, 异氰酸酯胶粘剂自制, 热压条件:温度170 ℃, 时间5 min, 压力3.5 MPa, 施胶量5.0 %, 含水率15.6 %, 板放置15 d后锯割, 锯割图如图 1所示。杨木边材试件, 25 mm ×25 mm ×14 mm, 弦向、径向、组合向各5块。25 mm ×25 mm ×20 mm, 弦向、径向各6块, 试件锯割图如图 2所示。落叶松试件, 25 mm ×25 mm ×12 mm, 弦向、径向、组合向各6块。25 mm ×25 mm×20mm, 弦向、径向各6块, 试件锯割图如图 2所示。
|
图 2 木材试件的切割图 Fig. 2 The preparing of wood samples 图中所画试件高度方向即为测量方向。The height direction of samples in fig.2 is the testing direction of TS |
木材试件先气干, 于45 ℃再烘干5h, 于(103 ± 2)℃烘干10 h, 要求选用试件在放大镜下观察无裂纹。
1.2 实验方法在恒温恒湿室内, 调节温度到20 ℃, 将试件浸入水中测其厚度膨胀率, 初期约每隔1 h测一次, 实验后期延长测量的间隔时间。每个试件总测量时间100 h左右, 数据点:刨花板44个, 木材22个。
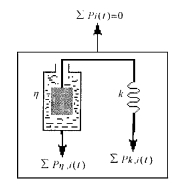
2 结果与讨论热压后的刨花板是一不稳定体系, 它存在内应力, 内应力将驱使体系向更稳定的方向转变, 若此时体系以膨胀功耗能量释放内应力(顾继友等, 2002a), 在宏观上就表现为厚度膨胀。而刨花板的厚度膨胀主要有:人造板内木材的粘弹变形恢复、人造板内木材的吸湿膨胀、胶接点破坏引起的变形及含水率存在较大变化时的机械吸附蠕变(顾继友等, 2002b)。木材作为一种天然高分子材料和其它高分子材料一样, 在力作用下, 将产生弹性变形和粘性变形。刨花板是一种以木材为主的复合高分子体系, 它所蕴涵的内应力作为一种特殊形式的力作用, 也将使刨花板产生类似的变形作用, 如图 3所示。
|
图 3 内应力作用下刨花板体系的受力模型图 Fig. 3 The action of internal force on particleboard system |
刨花板在内应力作用下, 体系内应力的合力为零, 但体系内的各微元却是受到一定的力作用, 即:

|
(1) |
在该力作用下, 刨花板内仍会产生对应的变形, 有:

|
(2) |
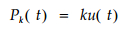
|
(3) |
则由(1)至(3)式有:
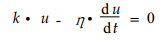
|
(4) |
将(4)式积分, 得:
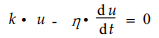
|
(5) |
(5) 式中:C是积分常数, τ=η/k。由此即得在任意时刻刨花板的瞬时厚度膨胀量, 形式上, 内应力与变形恢复量无关, 将(5)代入(2)或(3)及(1)中整理有:
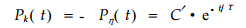
|
(6) |
式中:C'为常数。(6)式说明, 内应力是刨花板厚度膨胀的动力, 只要它存在, 且以膨胀功耗能量释放时, 刨花板就不免有厚度膨胀。
对(5)式在(t0, t)内积分, 即得刨花板t0时后到t时的厚度膨胀总量, 将之再与板的原厚U0相比, 即得t时的厚度膨胀率TS(t), 此值通过追踪测试刨花板和木材的吸水厚度膨胀率可得。即:
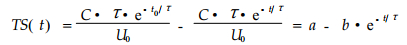
|
(7) |
以(7)式为基础, 编写程序, 通过代入τ值使得“ TS(t)———e-t/τ”线性化, 要求所有的点按最小二乘法原理尽量分布于直线的两边(即相关系数R2最大), 所得直线的斜率即为b, 其截距即为a, 方程得以确定。
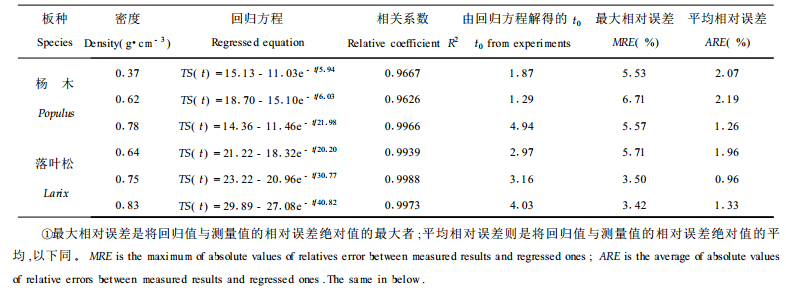
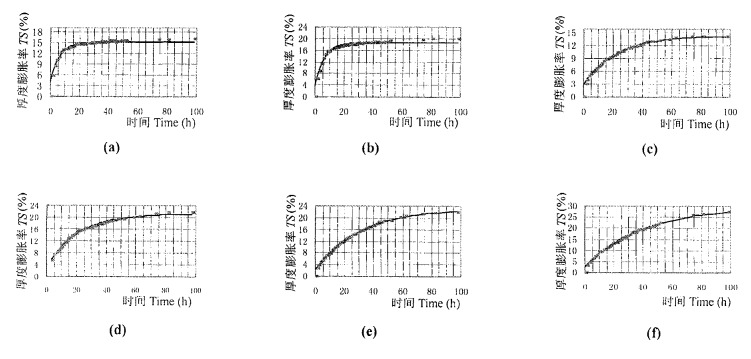
2.1 刨花板的厚度膨胀率方程将实验所测得的刨花板厚度膨胀率TS(t)进行回归, 结果如表 1、图 4所示。
|
|
|
图 4 不同密度杨木和落叶松刨花板的吸水厚度膨胀率与时间关系 Fig. 4 The relations of time and TS of particleboard with different density ——RR … TR. (a)、(b)、(c)为杨木, 密度分别为:0.37、0.62、0.78 g·cm-3, (d)、(e)、(f)为落叶松, 密度分别为:0.64、0.75、0.83 g·cm-3; RR和TR分别指回归值和测量值。 (a), (b) and(c)are Populus ' s with density of 0.37, 0.62 and 0.78 g·cm-3 respectively; (d), (e) and(f)are Larix ' s with density of 0.64, 0.75 and 0.83 g·cm-3 respectively; RR and TR in Fig. 4 refer to regressed results and testing results respectively. |
实验结果表明:不同密度刨花板的吸水厚度膨胀率在t0后能很好的满足回归的方程, 其测量值与回归值的最大相对误差在6.71 %以内, 亦即利用方程(7)能很好的描述刨花板的吸水厚度膨胀率规律, 并由此可预测刨花板的最大吸水厚度膨胀率, 即:
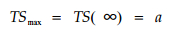
|
(7) 式中的参数τ, 按(5)式可称为蠕变迟滞时间系数, 按(6)式可称为松弛时间系数, 它是一个能反映刨花板尺寸稳定性而又具有动力学性质的参数, 由制造刨花板所使用的材料种类、刨花状态、胶种及热压工艺等共同决定。它的值越大, 则刨花板要达到最大厚度膨胀率的时间越长, 因此在一定时间内, 该刨花板的尺寸稳定性就越好。但是实验结果表明, 若要获得较大的τ值, 刨花板的密度就要越大, 这时对于一些密度大而又较硬的木材, 如落叶松因体系内蕴藏较大的内应力而造成最大厚度膨胀率偏大; 但对于密度较小材质较软的木材, 如大青杨由于较大的压缩率, 木材细胞压溃明显(王培元, 1992a; 1992b), 使得体系具有较大的τ值又具较小的最大厚度膨胀率。
(7) 式在刨花板中的应用, 强调在t0时后, 因为试件从浸入水中到t0时内, 由于起始条件变化大, 有突越现象。这也取决于目前的实验条件, 无法在实验初期取得更多更详细的数据点。在t0时后, 实验数据能与(7)式方程很好的吻合。
上述所研究的是刨花板试件浸入水中, 受热压锁定内应力及刨花板木材吸湿膨胀时膨胀应力共同作用下的情况。
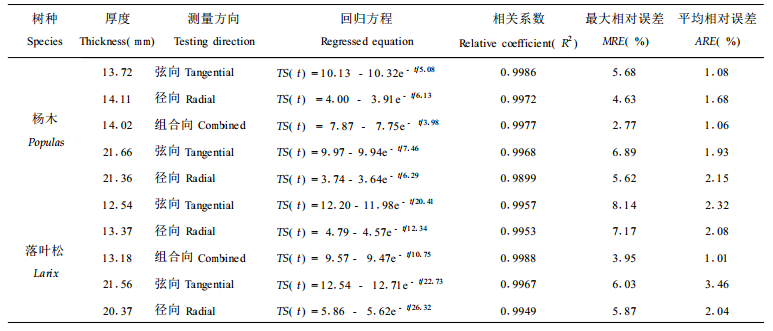
2.2 木材的吸水厚度膨胀率方程考虑到刨花板主要由木材组成, 因此将实验测得的不同时间的不同厚度杨木和落叶松试件的吸水厚度膨胀率, 也按(7)式进行回归处理, 结果如表 2、图 5所示。
|
|
|
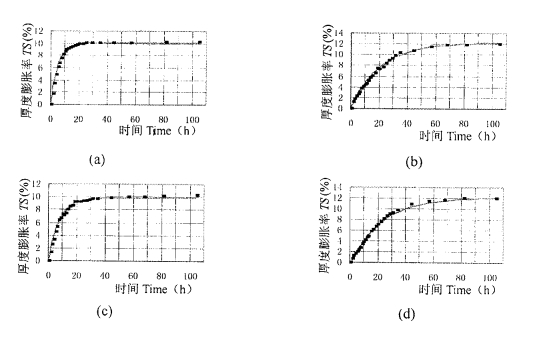
图 5 不同厚度杨木和落叶松的厚度膨胀率与时间关系 Fig. 5 The relations of time and TS of particleboard with different thickness — TR ——RR . 图 5中只列举杨木和落叶松的弦向情况, 其径向和径弦组合向情况的规律相同; (a)和(c)分别为13.5 mm和21.5 mm厚的杨木, (b)和(d)分别为12.5 mm和21.5 mm厚的杨木; RR和TR分别指回归值和测量值。 It only shows that of the tangential direction of Populus and Larix in Fig.5, other directions are the same; (a) and(c)are the Populus' s with the thickness of 13.5 mm and 21.5 mm respectively; (b) and(d)are the Larix' s with the thickness of 12.5 mm and 21.5 mm respectively; RR and TR in Fig.5 refer to regressed results and testing results respectively. |
实验结果表明, 不同厚度、不同取向的木材, 其吸水厚度膨胀率方程也能很好地符合(7)式规律, 其相关系数R2都在0.9899以上, 回归值与测量值间的最大相对误差在8.14 %以下, 平均相对误差的绝对值3.46 %以下, 因此可用(7)式方程很好的描述木材的吸水厚度膨胀率规律, 即:
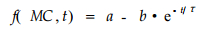
|
(8) |
实验结果表明, 把木材浸入水中后, 弦向和径向杨木的增重率(13.72 mm和14.11 mm)在1 h内基本上达到纤维饱和点, 分别为32.7 %和28.9 %, 组合向(14.02 mm)则需8.2 h达30.9 %, 而厚者在2.3 h后才达到31.3 %; 落叶松所需时间长些, 弦向和径向(12.54 mm和13.37 mm)分别在16.3 h和10.5 h才各达30.4 %和29.8 %, 组合向(13.18 mm)需18 h达29.6 %, 对于厚者则需24 h才达30.2 %。
这说明:当木材浸入水中, 较多的水分沿着木材相互贯通的细胞腔、细胞间隙、纹孔膜及细胞壁上的微毛细管以较快的速度进入木材的细胞腔内, 这些水多为自由水, 然后自由水再渐渐地通过毛细管作用、水蒸气扩散移动及结合水的表面扩散移动(李坚, 1994), 进入木材的细胞壁内, 形成结合水。这样, 木材虽具有较大的表观含水率, 而其吸水厚度膨胀率却是随着结合水的慢慢增加而逐渐产生, 即木材膨胀部分只有结合水形成之处。但由于形成结合水而膨胀的区域及其程度不可能在木材整体均匀地同时存在, 因此, 此时木材在膨胀的微小区域所产生的膨胀应力是逐渐产生, 性质类似与刨花板的内应力释放, 因此木材的吸水厚度膨胀率规律能很好地符合(7)式的推导。
由表 2所得回归方程可见, 在同一方向厚度不同的木材, 其最大吸水厚度膨胀率基本上相同, 这与客观事实相符; 但是对于木材的“蠕变迟滞时间系数” τ值的差别较大, 尤其是象落叶松等这一类密度较大、材质较硬的树种差别更大, 这主要是因为试件厚度不同, 水分在其中的扩散速率不同, 进而引起木材内所形成的结合水的量与木材绝干质量比的差异。
虽然素材的吸水厚度膨胀率能够说明刨花板中木材的吸水厚度膨胀率规律, 但应注意到, 刨花板内的木材, 经过一定热压时间的热、湿作用, 其物理化学性质有所改变, 宏观上表现出诸如刨花板的平衡含水率低于素材的现象(王逢瑚, 1997), 因此素材与刨花板内木材间存在一些差异, 但这不会影响素材吸水厚度膨胀率规律在刨花板木材上的应用。
2.3 刨花板内粘弹性变形恢复方程及胶接点破坏引起的变形方程木质材料的粘弹变形及其方程人们通常用凯尔文模型及其对应的方程来表示(王逢瑚, 1997), 即:
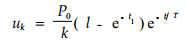
|
(9) |
因此在形式上, 它也满足(7)式形式, 或者说, (7)也可用于描述刨花板内木材的粘弹变形, 即粘弹变形方程形式上可写作:
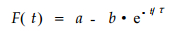
|
(10) |
把刨花板试件浸入水中, 将使刨花板热压时锁定于木材内的部分内应力释放, 加上木材吸湿膨胀所引起的膨胀应力, 如果这些内应力的和大于刨花板内胶接点的最大允许应力, 将会使胶接点发生破坏, 使胶接点所锁定内应力较彻底的释放, 同时产生变形恢复, 但由于邻近胶接点的束缚作用, 使变形未能完全恢复, 而形成新的内应力作用在邻近的胶接点上。因此其变形仍是内应力作用下的变形, 形式上也满足(7)式形式, 即:
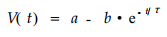
|
(11) |
对于机械吸附蠕变的形成本质, 目前不同的研究者(Gibson, 1965; Heamon, 1964; Mukudai, 1987; Nakano, 1996; Takemura, 1966)从不同的研究角度作出不同的解释。我们对机械吸附蠕变作出一定的解释(顾继友, 2000b), 但尚无法直接推导出机械蠕变方程, 然而, 依据(7)到(11)的方程及方程(12):
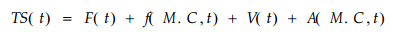
|
(12) |
有:
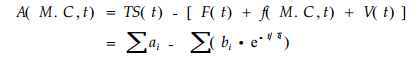
|
(13) |
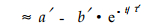
|
(14) |
式中, a'、b'、τ'为常数。将机械吸附蠕变精确式———(13)式中各项用麦克劳林级数展开, 取项数到测量精度内, 然后将之合并, 再用麦克劳林级数展开的逆过程, 将之还原, 可得到机械吸附蠕变的近似式(14)。由此, 就能较好的用已有的观点对之进行解释(顾继友等, 2002b)。
2.5 刨花板吸水厚度膨胀率方程的意义刨花板尺寸稳定性至少包含两层含义:1.它最大限度地膨胀能达到什么程度, 它表征刨花板吸水厚度膨胀率量的概念。2.它是如何达到最大膨胀, 它与时间相关, 表征刨花板吸水厚度膨胀率速率问题。但是参照有关标准, 目前人们都是使用刨花板的2 h或24 h吸水厚度膨胀率或二者同时使用, 来衡量刨花板的尺寸稳定性, 这样存在一些不足, 只能看到刨花板在2 h和24 h的吸水厚度膨胀率, 用之也只能定性描述刨花板所处时间的状态, 无法全面衡量和说明它的尺寸稳定性问题。例如在图 4中, 密度为0.37 g·cm-3的杨木刨花板和0.83 g·cm-3的落叶松刨花板, 在24.5 h的吸水厚度膨胀率分别为14.63 %和14.90 %, 二者相近, 但不能说二者尺寸稳定性也相近, 由图 4中的(a)和(f)及表 2可见, 落叶松板的最大吸水厚度膨胀率(29.89 %)要大于杨木者(15.13 %), 但是落叶松的吸水厚度膨胀速率(τ =40.82)要远小于杨木(τ= 5.94)。这些信息在以往标准中是无法得到。因此用吸水厚度膨胀率方程衡量刨花板的尺寸稳定性将更合理更实用。由刨花板吸水厚度膨胀率方程来定义理想的刨花板(尺寸稳定性好)为:具较小的最大吸水厚度膨胀率(a值)同时具有较大的蠕变迟滞时间系数(τ值)。
3 结论不同密度刨花板的吸水厚度膨胀率规律可用如下方程形式描述, 由之而得的回归值与测量值的吻合性很好, 其相关系数R2都大于0.96以上, 而相对误差较小。
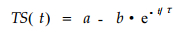
|
木材的吸水厚度膨胀率方程、粘弹性变形恢复方程、胶接点破坏引起的变形方程的形式也都符合刨花板吸水厚度膨胀率方程形式, 对于机械吸附蠕变方程通过数学变换, 也可获得相同的数学形式。对应方程的形式可写作:

|
应用刨花板的吸水厚度膨胀率方程, 利用方程中的a值能很好的预测刨花板的最大吸水厚度膨胀率, 同时利用参数τ值说明刨花板尺寸稳定性, 因此利用该方程衡量刨花板的尺寸稳定性更具合理性和实用性。
利用刨花板吸水厚度膨胀率方程衡量刨花板尺寸稳定性时, 只要预先获得该板吸水厚度膨胀率的几个点(建议取点时间在浸水后3 h开始, 点宽些, 且点的数目越多越好), 利用数学方法, 求出方程中的a、b及τ值。
顾继友, 高振华, 王逢瑚, 等. 2002a. 刨花板厚度方向变形研究Ⅰ.人造板应力释放之化学热力学研究初步. 林业科学, 38(2): 152-156. |
顾继友, 高振华, 王逢瑚, 等. 2002b. 刨花板厚度方向变形研究Ⅱ.刨花板厚度方向变形模型的建立及释因. 林业科学, 38(3): 160-166. |
李坚, 等. 1994. 木材科学. 哈尔滨: 东北林业大学出版社, 175-177.
|
王培元, 郭继红. 1992a. 刨花在压缩力下变形状态的研究Ⅰ.大片刨花压缩流变性能的研究. 林业科学, 28(4): 323-329. |
王培元, 郭文莉, 郭继红, 等. 1992b. 刨花在压缩力下变形状态的研究Ⅱ.杨木刨花压缩力学行为对刨花板质量影响的分析研究. 林业科学, 28(5): 415-421. |
王逢瑚. 1997. 木质材料流变学. 哈尔滨: 东北林业大学出版社, 14~15:57~58.
|
Gibson E J. 1965. Creep of wood:Role of water and effect of a changing moisture content. Nature, 206: 213-215. DOI:10.1038/206213a0 |
Heamon R F S, et al. 1964. Moisture content changes and creep of wood. Forest Prod.J, 14: 357-359. |
Mukudai Y. 1987. Modeling and simulation of viscoelastic behavior (bending deflection)of wood under moisture change. Wood Sci.Technol, 21: 49-63. |
Nakano T. 1996. Viscosity and entropy change in creep during water desorption for wood. Wood Sci.Technol, 30: 117-125. DOI:10.1007/BF00224963 |
Takenmura T. 1966. Plastic properties of wood in relation to the non-equilibrium states of moisture content. Mem Coll Agric Kyoto Univ, 88: 31-48. |
 2002, Vol. 38
2002, Vol. 38