在单板旋切中, 选择最佳的定心点是旋切优化的最关键技术。本文在原木三点和四点定心理论的基础上, 提出了旋切原木的六点定心理论。该理论的提出将使原木定心理论从圆截面发展到椭圆截面, 从而提高了原木定心理论的水平。

1 椭圆抛物柱原木的数学描述方法

从大量的统计分析理论可知, 原木横断面有59.6%为椭圆(圆是椭圆度q_e=1的椭圆)。其它形状中, 圆占2.8%, 蛋圆占13%, 三角形占11.7%, 四边形占10.2%。这几种形状中很大部分近似为椭圆。所以有近97.3%的原木截面近似为椭圆(马岩, 1996)。从干曲线的分析可知, 抛物线, 凹曲线, 直线, 指数曲线和对数曲线都可以看作是连续幂曲线。所以, 本文中定义:旋切原木横断面为椭圆或近似为椭圆, 椭圆度为常数, 纵断面为幂曲线, 树干中心线为直线, 其它缺陷略去不计, 这样的原木称为理想原木。

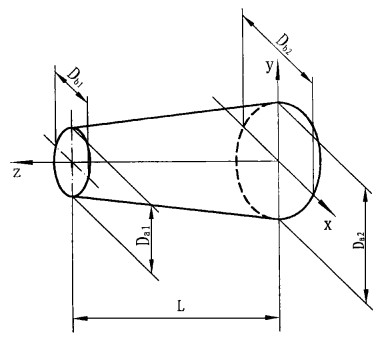
假设:原木的形状是理想原木(见图 1), 取原木的小头长径D_a1、小头短径D_b1、大头长径D_a2、大头短径D_b2和材长L为实测值, 则理想原木的数学模型为:

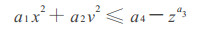
(1)

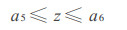
(2)

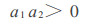
(3)

式中:a₁为椭圆长轴系数; a₂为椭圆短轴系数; a₃为截顶椭圆锥体系数; a₄为截顶椭圆锥体方位系数; a₅为截顶椭圆锥体下起始点系数; a₆为截顶椭圆锥体上截至点系数。(1) ~ (3)式构成了理想原木的包络空间, 从数学的定义上讲, 该式为截顶椭圆幂曲线的原木数学模型。

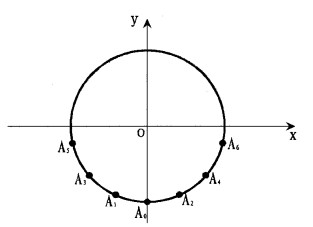
2 原木旋切时的检测点的坐标变换和转换坐标的计算方法

本文的研究是为旋切原木智能定心机研究的基础理论, 在实际机器设计中, 为了消除检测误差, 我们的检测点是按图 2方式选取, 图中A_i为测试点, i=0, 1, 2, 3, 4, 5, 6。

在原木放在坐标系中之后, 由视频技术可以测出D_a1, D_a2, D_b1, D_b2, L。在Z=0的截面内, 我们取7个点, 这7个点满足下列条件:

(4)

由于最佳原木中心和任意放置中心不同心, 则(1)式中x, y将发生变化。(1)式变成下列形式:

(5)

式中:b₁为最佳中心沿x方向的偏移距离; b₂为最佳中心沿y方向的偏移距离; α为最佳中心的x轴相对原坐标的偏移角。

将A₂的坐标(x₂, y₂, L₂)代入(5)式可得:

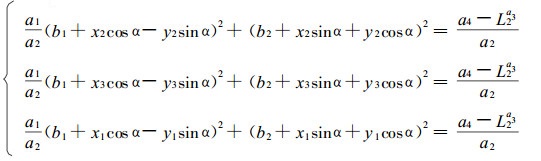
(6)

设:

(7)

为了判定(7)式的非奇异和收敛性, 需建立(7)式的雅柯比矩阵, 对(7)式求偏导数:

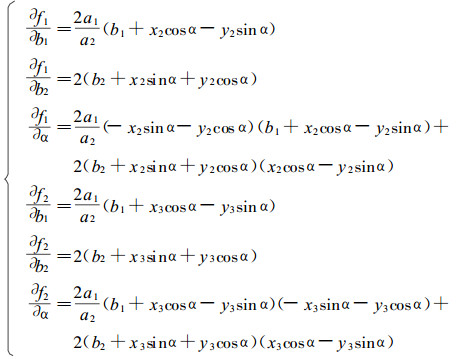
(8)

同理可求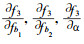方程(7)的雅柯比矩阵:

(9)

采用牛顿法可求解方程组(6)式, 从而得出该截面X方向偏移量b₁, Y方向偏移量b₂和椭圆对称轴和坐标系的最小偏转角α的数值。求出b₁, b₂和α以后, 则实测点的坐标可以变换到原木描述的理论坐标系中:

(10)

同理, 可以做出其它截面的坐标变换(王坤, 1987; 徐士良, 1993)。

3 六点回归椭圆截面的数学描述理论

如果在一个截面内任取6个点, 就可以回归出一个椭圆。

由视频检测以后, 可以测出这个截面的两个参数D_a2和D_b2, 由它们和D_a1、D_b1及L可以建立(1)式的数学模型。由于视频检测会有误差, 原木本身不是标准椭圆又会产生出一些模型误差, 加上仅在一个截面内检测了4个点, 又有长短径选择产生的误差。所以, 用6个检测点回归出一个椭圆, 再用这个椭圆对理论椭圆进行修正, 就可以提高检测的精度。将(6)式写成下列形式:

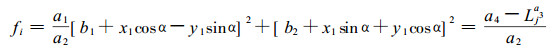
(11)

式中, i=1, 2, …, 6, j=1, 2, 3, 4

将6个检测点的数据代入(11)式, 可以得出一组非线性方程。采用牛顿法求解出这个方程组, 就可以求出一组参数:

其中, k为k组数据回归出的k椭圆的数据。

由该组数据可以求出原木的实测参数:

(12)

在实际检测中, 我们取了7组数据。由7组数据组合6个参数的数据可以有7种方法。加上视频检测的1组数据, 共计8组数据。将这8组数据取平均值, 就是1组近似最理想的椭圆的回归数据, 我们定义这组数据为:D_A1, D_B1, D_A2, L。它们的坐标转换为:B₁, B₂和α。

当然, 在实际工程中, 还要设定一个误差量, 当误差超过该值时的那组数据将被略去。由这组理想数据可以求出原木的材积为:

(13)

近10年来, 国外利用离散矩阵的方法进行线性仿真来描述原木。这种方法需要大规模光电检测装置、大容量计算机、快速检测和处理大量实测参数, 尽管已研究了十几年, 但应用前景一直不佳。采用激光检测旋切原木时, 先让原木旋转360°, 才能检测出全部数据, 这在未定心之前是很麻烦的。使定心机的结构复杂, 功率大, 定心成本高。一般发展中国家, 在短期内不可能采用这种理论和方法。

采用简单的2次分段连续函数的仿真方法描述任意弯曲原木, 由于是2次仿真, 更接近于原木断面曲线连续的实际情况, 所以, 在同样实测参数下, 2次仿真比国外线性仿真方法的精度要高得多。如果线性仿真要达到它的精度, 实测参数至少要比2次仿真增加近10倍。因此, 提高仿真的次数, 是减少实测参数、简化数据处理和提高计算速度的最好途径(马岩, 1996)。

4 结论

本文提出的六点定心法适合于97%以上原木的截面形状, 精度高于三、四点定心的理论和方法。

六点定心的检测参数少, 且精度远远高于线性仿真的回归精度。这样, 可以简化检测系统。

如果采用7点检测, 用6点回归椭圆, 采用组合平均的方法, 可得到近乎优化的椭圆回归结果。

本文提出的原木4截面模型从整体上描述了原木, 特别考虑了弯曲对旋切的影响, 为旋切优化提供了数学模型。

本文提出的理论和方法使定心机从机械→几何→光学→激光数控发展数控多媒体定心的阶段, 可以使原木在不转动的条件下实现定心, 使定心精度和定心优化的效益又有所提高。