文章信息
- 胡新生.
- Hu Xinsheng.
- 群体遗传结构的理解
- A REVIEW ON UNDERSTANDING THE GENETIC STRUCTURE OF POPULATION
- 林业科学, 2002, 38(2): 119-128.
- Scientia Silvae Sinicae, 2002, 38(2): 119-128.
-
文章历史
- 收稿日期:1998-09-28
-
作者相关文章
生命世界由许多不同的物种组成, 这些物种又是由许多群体组成, 群体是由在时间和空间上共存的个体聚集而成的。群体内的个体表现出不同程度的遗传变异, 这种变异又是由有性繁殖、个体间遗传物质交换等作用的结果。在任一情况下遗传变异程度和模式取决于许多因子, 如该种的交配系统, 群体间的基因流, 以及受遗传漂变和自然选择所修饰, 因此在群体的动态变化下, 遗传变异也呈现出动态变化行为, 理解这种遗传变异行为正是群体遗传学的目的。因此群体遗传变异理解成为一些应用目标如选择育种等基础, 是遗传资源保护经营的基础。
改变遗传变异动态性的因子是多样化的, 包括突变、交配系统、遗传漂变、基因流动及自然选择。突变是所有变异的来源, 交配系统将这种变异进行分类并确定群体内遗传结构(Wright, 1951), 然而遗传漂变导致基因频率的随机波动, 然而导致变异丢失及隔离群体遗传分化加剧(Falconer, 1989)。基因流动可以使不同群体基因频率趋同, 自然选择修饰基因频率, 以使群体内和群体间适应于环境。在这些因子之间, 突变、基因流动和自然选择以一种在数量上和方向上可预测方式改变着基因频率, 使基因频率产生系统变化(systematic change)(Wright, 1969)。然而遗传漂变效应在数量上可以预测, 但在变异方向上不可预测, 它使得基因频率随机变化(random change)。通常这些因子可同时作用于一个群体, 因此群体遗传学是理解这些因子相互作用的基础。
群体遗传学必须产生于群体的框架内, 在一特定的一系列空间群体或个体内生效, 而非于一个抽象的世界内出现。为了模拟真实的世界, 必须理解支配这些遗传变异的过程是怎样在一些尽可能反映现实世界情况下的不同空间群体类型内作用的。至今还没有一个模型能用于描述所有的情形, 因此, 一系列不同的群体模型框架已被设计出来了, 用于研究遗传结构的动态性, 这些包括下面要阐述的岛屿模型(island model), 步石模型(stepping -stone model)和距离隔离模型(isolation by distance model)。
除了这些群体框架外, 还需要共同语言描述和比较遗传变异行为。最简单的情况是描述基因频率的变化, 单个位点遗传结构及群体内多位点遗传结构。目前已有多种方法来描述空间结构变异(Wright, 1969), 如用近交系数定义的Fst来定量描述群体遗传分化程度。
应用这些遗传变化过程、群体结构框架及共同语言, 就可以描述遗传变异行为。本文的目的在于评述一系列群体结构模型, 阐述人们是怎样模拟现实群体的, 这些模型又是怎样帮助我们去推测实际情况的, 它们的缺点及可能的发展, 我们又如何来测定我们的理解, 以及这些模型的实际应用。
1 岛屿模型及其异体 1.1 岛屿模型岛屿模型是一重要的用于描述现实群体的经典模型, 它可能是模拟自然遗传分化群体的最简单的方式, 但在产生其它群体遗传结构模型中起重要的作用。该模型的理论结果仍广泛应用于实际工作中。岛屿模型原始思想是由Wright在他的一篇具历史意义的论文“Evolution in Mendelian Population”(1931)提出的, 以后得到进一步发展(Wright, 1943; 1951)。
该模型的基本思想是假设一个群体分化为无限多个地方小群体(亚群体), 每个亚群体的有效大小N, 亚群体在空间呈离散分布, 每个亚群体接受一小部分来自整个群体的迁移个体(m)。这里需要指出的是迁移个体为二倍体(核基因位点)。迁移率与迁移基因频率在任一世代内假设为常数(见图 1)。由于亚群体大小有限, 遗传漂变将导致亚群体间分化, 然而稳定的迁移却使这一分化过程受到阻止, 最后迁移与遗传漂变达到平衡, 群体维持在平衡状态, 同样基因频率在亚群体间的分布也达到稳态。

|
图 1 岛屿模型示意图 Fig. 1 A schema representing island model 圆圈表示亚群体, 线箭头表示远距离的基因迁移。 White circles represent sub-populations and line arrows stand for long-distance migration. |
以此模型为基础, Wright(1951)引入了F-统计量, 它提供了一个简单的方法来概括群体结构, F-统计量已成为群体遗传学公共语言。这儿引用Wright的记号, Fit和Fis依次用于表示整个群体和亚群体的近交系数, 而Fst用于表示亚群体间遗传分化程度的近交系数。该模型两个重要结论是:①整个群体近交系数可剖分为亚群体内和亚群体间, 且存在着1 -Fit =(1 -Fis)(1 -Fst)的关系; ②Fst与基因迁移数(Nm)的关系, 即Fst =(1 +4Nm)-1。这两个著名公式为群体遗传结构分析奠定了坚实的理论基础。
由于存在许多假设, 该模型与实际情况有些距离。这些假设有:①无限数目的亚群体; ②稳定的群体大小(N); ③群体无消失和重建发生; ④恒定的迁移速率; ⑤恒定的迁移基因频率; ⑥适合于一个位点两个等位基因简单情况; ⑦随机交配; ⑧适合于选择性中性基因; ⑨二倍体核基因; ⑩离散的世代。
1.2 约束条件与拓广岛屿模型许多假设条件已逐渐得到了释放和发展, 以更适用于现实群体。例如假设①是不现实的, 因为亚群体的数量应该是有限的, 这一条件已在有限岛屿模型得到了发展(Nei, 1975; Takahata, 1983; Takahata et al., 1984)。在这种有限的岛屿模型情况下, Fst与迁移基因数(Nm)及亚群体个数(L)的关系已得到拓广。其它的一些假设在一些更接近实际的模型中也得到了发展(见表 1)。
|
|
对于岛屿结构模型, 在理论上许多遗传变异特点已被研究过, 例如有限岛屿结构模型中维持的有效等位基因数(Maruyama, 1970)及有效群体大小(Nei et al., 1993)。该模型在实践的一个重要应用就是它提供了一种简单方法用于间接估算亚群体间的平均基因迁移数(Nm)(Slatkinet et al., 1990)。
至今已采用不同方法来将岛屿模型推广到植物群体上。Petit等(1993)采用类似于Birky(1988)方法探讨了有限岛屿模型, 该方法与Wright(1951)所用的方法不一样。Wright(1951; 1969)采用通径分析或基因频率方差方法获得了F-统计量, 而Petit等(1993)通过分析基因多样性组成入手, 获得了Gst(Wright) Fst在一个位点多个等位基因情况下的表达式。Ennos(1994)从分析植物群体基因迁移的组成入手分析了无限数目岛屿模型, 并获得一重要的关系式, 用于描述亚群体间花粉流与种子流的比值与F-统计量的关系。例如, 在植物群体中, 单亲遗传基因(母本遗传基因)的群体遗传分化Fst =(1 +2Nm)-1, 式中, m=ms(种子迁移率), 因为母本遗传基因的迁移只有通过种子流动进行。因此基于这些分析, 有必要建立用于描述单亲遗传标记和二倍体核标记的植物群体遗传结构模型。
1.3 岛屿模型的异体如果将整个群体分成为两块, 一块是一个亚群体, 其余亚群体统看成另一个群体, 这时岛屿模型就变为大陆-岛屿(mainland-island model)(Hanski et al., 1991; Hanski, 1994), 有时这种结构由一个大陆群体和几个环绕大陆群体岛屿群体组成, 因此大陆-岛屿模型实际上是Wright的岛屿模型的异体。大陆-岛屿模型最明显的特点是群体大小存在巨大差异, 大陆群体表现稳定和没有消失(extinction)特点, 而岛屿群体有大的消失可能性, 因此, 如果从岛屿群体到大陆群体的迁移够小的话, 那么大陆与岛屿群体间关系类似于源群体(source)与库群体(sink)的关系(Gaggiotti et al., 1996)。若岛屿群体不存在消失问题的话, 随机的基因迁移影响将导致岛屿与大陆群体之间动态遗传结构关系, 因此, 大陆-岛屿模型将有助于研究有关岛屿群体遗传资源保存问题。
岛屿模型的另一种异体就是巨型群体模型(metapopulation structure), 该模型结构起初由Levins (1970)提出的, 亚群体内的大多数个体发生形成与死亡过程, 一旦亚群体灭亡后, 邻近亚群体会迁移过来并重新建立新的亚群体, 一系列由这种群体并由个体迁移而相联系综合体称为巨型群体(Hanski et al., 1991; Hanski, 1994; Gilpin, 1991; Hansson, 1991)。这种类型的群体结构已被用于研究亚群体消失与重建对遗传分化影响上, 有关这方面研究近几年才有报导(Wade et al., 1988; Whitlock, 1992; Rannla et al., 1995), 这方面研究在今后有很大的潜力, 尤其是在植物群体上(见第6部分)。
2 步石模型步石模型是由Kimura(1953)提出的, 随后才建立其理论基础(Kimuraet et al., 1964; Weiss et al., 1965)。该模型描述了这样一种情形, 即一个群体分化为无限多个亚群体, 在每个亚群体内发生随机交配, 群体间的基因交换发生在相邻近群体间及在整个群体上(长距离的基因流动)(见图 2)。若不存在相邻亚群体之间的基因流的话, 步石模型就转变为岛屿模型, 因此岛屿模型是步石模型的特例, 步石模型的优点就在于它考虑到了邻近群体的基因流, 因而更接近自然的真实情况。一种比较明显的生物现象就是生活在相近处的个体间要比生活在更远处的个体间看起来更相似, 这种思想可以用基因频率相关性随空间距离变化而改变来加以描述, 可能正是这种原因, 除了用基因频率的方差表示外, 基因频率相关性被用于描述群体的空间变异。

|
图 2 步石模型 Fig. 2 Stepping-stone model (a)一维空间情况; (b)二维空间情况, 在两种情况下, “ m1”表示邻近群体间的迁移, “m0”表示远距离迁移, 迁移库来自所有亚群体的微小贡献。 (a)One dimension case.(b)Two dimension case.In both cases, the " m1" stands for migration from neighbourhoods.The" m0" stands for migration from long distance dispersal.The migrant pool comes from small contributions of migrants from all of the local population. |
在步石模型中, 理论上已证明基因频率相关性随空间呈负指数变化(Kimura et al., 1964), 且这种相关性明显受空间维数影响。这种定性结论有助于正确理解自然群体结构, 具有重要意义。将基因频率空间变化当作连续性变异看待, Malécot(1948; 1969)获得了类似的定性结论。应该指出的是三维空间情形不太适合描述植物群体结构。在实际应用时, 遗传相关随空间距离变化是很难测定的, 这是由于很难获得在时间空间上基因频率的期望值E(P)。然而E(P)的估值可以近似地用所调查的所有群体基因频率的均值加以估算。重要的是这时所得到的值是指特定的时间和空间下获得的, 并不是理论上所有的期望值(在无限亚群体上的), 使用这一估值我们可以近似估计基因频率相关性随距离的变化。
步石模型现已广泛地被应用于群体结构模型上, 尤其是在理论研究方面。一些有关步石模型结构的群体遗传变异特点已进行了研究, 包括对经典假设条件的拓广。例如, 经典的无限数目亚群体假设已被拓广到有限数目亚群体的步石模型(Maruyama, 1970)。Maruyama等(1980)证明若亚群体的消失与重建发生很频繁的话, 整个群体的有效大小会减小, 且群体分化受阻。同样也证明若迁移发生很频繁, 有限岛屿与步石模型表现出非常相似的群体内和群体间遗传变异(Nagylaki, 1983; Crow et al., 1984)。
与岛屿模型类似, 步石模型的许多遗传变异特点今后仍需要研究, 如连锁与重组效应, 随机迁移效应等。
3 距离隔离模型及其相关模型一种与岛屿和步石模型所描述的情况相反的群体分布是在空间上连续分布, 但由于有限的短距离基因迁移, 个体间交配局限于小范围内进行。远距离分开的不同个体群由于有限距离的基因迁移而产生遗传分化, 这种现象正是距离隔离模型所要描述的(Wright, 1940; 1943), 该模型强调空间距离的隔离的作用及群体遗传分化的形成, 因此距离隔离模型提供了一个框架用于理解在空间连续分布的群体遗传结构。
该模型的一个重要参数就是邻近群体大小(Nb), 它被定义为一定范围内的个体数量, 该范围内分布中心个体的亲本可以被看成为从中随机抽取的个体(Wright, 1943)。一个关键的假设就是在过去世代t时, 邻近群体大小为tNb(二维空间)和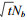

|
图 3 距离隔离模型示意图 Fig. 3 Schematic diagram showing the change of neighbourhood population size 在二维空间内Nb随过去时间t而变化。Nb大小与过去世代t呈线性变化, 图中的圆圈示邻近群体大小, 方块中的小点表示个体在空间上均匀分布。 Nb with past timet in two dimension space.Neighbourhood population size linearly increased with generation in the past. The circles represent the size of neighbourhood.The dots in the block stand for individuals uniformly distributing in space. |
与岛屿模型类似, 若在任一祖先世代t内的邻近群体大小内存在来自整个群体的远距离迁移的话, 这将存在迁移与漂变平衡, t邻近群体之间遗传分化将达到稳定状态, 同样基因频率分布也将处于稳态, 这时群体分化的度量可由Fst =(Fit -Fis)(1 -Fis)计算而得(Wright, 1943; 1969)。
一个重要的影响邻近群体遗传分化的因素就是交配系统, 它通过影响近交系数而影响遗传分化(Wright, 1921; 1943; 1946)。Wright(1946)已研究了一系列交配系统的影响, 但一个重要的假设就是在所有的邻近群体内交配系统是同质的, 然而实际的交配系统在空间上有可能是不同的, 这是由于许多因素如群体年龄结构等影响交配系统。
除了研究群体在空间密度均匀分布的情况外, 距离隔离模型还可以进行修饰以适合于分析空间上随机分布的团块(cluster)分布类型, 每一个团块与邻近团块有一小部分基因交换(基因流动)(Wright, 1969; 1978)。于是前面所述的距离隔离模型就转化为空间上块状分布的群体(cluster model)。这与步石模型类似, 但采用了完全不同方法和途径(Wright, 1969; 1978)。
同样有许多问题存在于距离隔离模型中需要解决:①由于缺乏群体密度调节规则, 子代随机迁移导致下一世代群体分布出现团块状(clumping), 这与初始群体在空间均匀分布假设矛盾(Malécot, 1969; Felsenstein, 1975); ②在过去世代t内, 邻近群体大小假设需要在数学和生物学上作出证明和解释, 当应用植物群体时, 若考虑种子和花粉流动时, 邻近群体大小计算变得十分复杂; ③近交系数的计算是采用通径分析和假设配子对杂合子作用为线性(linear), 完全的(complete)及均等的(equal)条件下获得的(Wright, 1921; 1969; Li, 1976), 通径系数的获得是在假设由杂合子到卵子和精子, 或从卵子和精子到杂合子有相等效应的条件下进行计算的。例如, 若精子与卵子上的基因存在显性效应的话, 就不可能获得本模型中一关键的表达式, 即b1b2=(1 +F′)/2, 式中b1和b2为从杂合子到两个配子的通径系数, 而F′为两个组成杂合子的配子间的相关系数。
然而, 距离隔离模型仍广泛应用于连续分布的群体之中, 邻近群体大小概念提供了理解空间连续性分布自然群体的一种方法, 例如这一模型思想已被应用于计算从连续分布群体中随机抽取若干基因的共祖并合时间概率(probalility of coalescent Time)(Bartonet et al., 1995)。
很容易理解群体遗传分化与空间地理距离呈正向关系, 或群体分化与基因迁移数呈负向关系(Slatkin, 1987)。然而其分析表达式却难以获得。已有一些方法或模型用于检测距离隔离效应(Sokal, 1978a; b; 1979; Slatkin et al., 1990)。其中一种方法就是将遗传数据与地理上邻近群体间距离进行相关分析———空间自相关分析, 该分析可用于检测空间分布类型和距离隔离的可能性, 及估计团块状大小(Sokal, 1978a; b), 但必须理解到空间自相关分析并不是一个遗传模型而是纯统计模型, 这种分析并不是建立在空间分布类型是怎样产生基础上的, 但可作推测。然而Barbujani(1987)却证明在给定距离内基因频率空间自相关系数(Moran′I)是该距离上亲属关系系数(Kinship)的直接函数(f)及基因频率标准值方差(Fst)的反向函数, 即I =f/Fst。从某种程度上说, 这种函数关系有助于深入理解空间自相关系数的内涵。
采用计算机模拟方法, 在许多不同的群体结构模型下(离散分布群体)Slatkin等(1990)找到一种线性函数, 用于描述有效基因迁移数(M =Nm)与地理距离(d)的关系, 即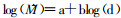
以上介绍的三种模型代表了建立于理论假设基础上的一般模型, 另一种研究群体遗传结构的方法是测定田间实际群体遗传结构模式, 并建立模型用于说明所观测到的结果。一种通常观测到的自然遗传结构就是渐变群结构, 即基因频率是研究群体所处地理位置的函数, 一个典型的渐变群就是基因频率随地理距离表现梯度变化(见图 4)。这方面的研究是一个很早的领域, 但仍然是进化研究的重要方面, 尤其是在与物种形成的关系方面。渐变群可以存在于杂交区内(hybrid zone)(Young, 1996), 或在其它的情况下存在(Millar, 1983)。渐变群的起源是非常复杂的(Endler, 1977), 根据Endler(1977)的描述, 渐变群是物种形成过程中的一个临时阶段。有3种类型的物种形成路径可以产生这种临时的阶段:群体内的物种形成(sympatric)、生殖隔离物种形成(parapatric)、地理隔离物种形成(allopatric)3种物种形成方式(见图 5)。一个祖先物种可以在空间异质环境上扩散或发生扩散。若扩散发生, 空间上遗传分化将会发生, 并有可能导致两种情形。一是扩散群体仍然存在相互接触(连续性区域), 但相邻接触区域的群体遗传分化仍继续形成(生殖隔离物种形成parapatric)并导致渐变的群体(梯度平稳变化)形成和急剧升降变化群(在连接处)形成。另一种是扩散后群体彼此分离(disjunct), 遗传分化在隔离状态下形成(地理隔离物种:allopatry), 群体分化后到一定程度时可以再次相遇(二次接触:secondary contact)并产生渐变群。若祖先物种并不在空间上进行扩散, 空间分化不会形成, 但是群体内的物种形成遗传分化会发生, 这是由于生态上(如生境选择)和时间隔离等原因所致, 因此渐变群可以在分化群体相邻接触区域形成。3种渐变群形成的路径可以概括为图 5。

|
图 4 一个典型的渐变群示意图 Fig. 4 Schematic diagram of a typical cline 基因频率随地理距离梯度变化, 横坐标上的数值也可表示不同群体所处的地理位置。 The gradual change of gene frequency with geographical distance.The numbers labelled along abscissa can also stand for geographical positions at which different populations locate. |

|
图 5 渐变群形成的可能途径(根据Endler(1979)绘制) Fig. 5 Possible paths to form of cline, redrawn after Endler (1977) 祖先物种Ancestral species; 无地理扩散No geogrphical; 地理上扩散Spreed; 区域扩散Range expansion; 二次接触Secondary contact; 渐变群形成Fornmation of cline; 群体内的物种形成Sympatry; 生殖隔离物种形成Parapatry; 地理隔离物种形成Allopatry. |
前面提到的三大经典模型不能用于解释渐变群的形成, 因此, 在理论研究上理解这种自然现象是一重要的内容。这方面理论研究可追溯到Fisher(1937)先驱工作, 他研究了优势基因向前扩散的波动性。采用基因扩散行为与自然选择的综合作用, Fisher(1937)找到了波动前进速率, 选择优势与扩散标准离差的关系式, 即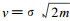
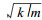
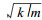
已有许多有关研究(Haldane, 1948; Fisher, 1950; Slatkin et al., 1975; Nagylaki, 1975; 1976; 1978a; b;Felsenstein, 1975; Barton, 1979; 1983; Barton et al., 1989), 然而在多数的研究中, 扩散模型被用来近似模拟渐变群形成, 目前对于渐变群形成理解主要是基于扩散与选择的综合作用基础上的。
渐变群体形成的内在遗传机制是很复杂的, 在自然界, 若渐变群存在已有很长时间的话, 那么就一定有某种平衡机制来维持它, 否则渐变群将最终消失。目前认为一个重要的遗传机制就是选择—迁移—漂变平衡。若只存在一种纯漂变过程, 或漂变—迁移过程, 渐变群是不可能形成的。如果存在选择作用但是太弱, 或迁移的影响太大的话, 渐变群也不可能形成, 因此随地理空间变化的自然选择强度是决定渐变群形成的一重要因素。Nagylaki(1975)对渐变群形成的一些条件进行过研究。
在确定渐变群形状时有两个重要的参数, 若漂变或漂变影响很小, 可以忽略不计的话, 那么在一给定的选择系统下, 特征长度决定了渐变群的宽度。特征长度越长, 渐变群就越宽。若遗传漂变影响不能忽略的话, Nagylaki(1978a)获得了另一重要的无量刚参数β, 用以说明选择与随机漂变的相对重要性, 即β =2ρσ2/c, 式中ρ为群体的空间密度, σ2为扩散方差及c为一确定渐变群的特征长度。实际上β是一迁移和选择作用的自然距离(2ρσ2)与确定性渐变群特征长度(c)的比率, 如果β≫1(β≪1)的话, 与随机漂变影响相比选择作用是强的(或弱的)。类似于阻碍基因流动的障碍, 渐变群实际上阻止了或推迟了相邻群体之间的基因交换。一个渐变群可以向前或向后移动, 表现出动态性(Barton et al., 1989)。渐变群内的遗传结构可以提供许多有关群体形成历史方面的信息。
今后有关渐变群形成的许多理论问题仍需要研究, 其中一个重要研究方面就是将现有的渐变群论推广到植物种上, 由于花粉和种子流动影响植物种的渐变群形成表现复杂的“定殖(colonization)”历史, 因此分析植物种渐变群有关信息有助于深入理解群体形成历史(见第6节分析)。
5 群体遗传结构测定群体遗传结构模型可用于测定预测实际群体, 并用隐含的生物学过程来解释所观测到的群体遗传结构和估计一些参数, 如群体之间的基因流, 然而为了测验群体遗传结构理论及作出生物学的推测, 我们需要测定实际群体, 为此需要采用种内自然界已存在的遗传标记来进行分析。遗传标记可以包括形态特征, 生理生化特征, 染色体核型变异, 同功酶变异及DNA序列差异标记, 这些标记已不同程度地应用到了群体遗传结构的研究上(Avise, 1994; Mallet, 1996), 近几年随着PCR(polyherase chain reaction, 聚合酶链式反应)(Mullis et al., 1986)的技术应用, 许多基于PCR反应的不同类型的DNA标记已产生, 如RAPD标记和SSRs(simple sequence repeats, 简单重复序列)标记(Rafaalski et al., 1993), 随着不同的反应引物的研制(Strand et al., 1997; Dumolin-Lapegue et al., 1997; White, 1996; Morgante et al., 1993; Hadrys et al., 1992), 许多不同类型的标记将出现, 这将有助于在更基础的水平上去调查群体遗传结构。
6 经典模型在植物群体上拓广前面已经强调了各种不同的模型提供了不同的方式去认识群体遗传结构, 但至今很少模型可用于探讨植物群体遗传结构上(Wright, 1969; Petit et al., 1993; Ennos, 1994), 初看起来, 这会使人感到诧异的, 可能的原因是植物群体遗传学总是滞后于动物群体遗传学, 通常的情况是动物群体遗传理论在植物上进行简单地应用, 然而一些有关植物群体的重要问题是不适合套用动物群体遗传理论的, 本节将强调将经典群体遗传结构模型拓广到植物群体上的必要性。
在植物和动物群体遗传结构方面, 存在许多明显不同的地方。首先, 植物群体基因流载体与动物不同, 大多数植物基因迁移发生在两个阶段上:即种子和花粉流动, 这两种基因流可发生同一世代内, 首先发生花粉流动, 种子形成, 随后种子流动发生, 因此植物群体的基因流动可以通过种子流进行, 或花粉流动进行, 或两者都有。种子和花粉流动的水平在时间和空间上是可变的, 且因树种群体而不同。例如, 在加拿大的一针叶树种太平洋冷杉(Abies amabilis), 近交水平变化很大, 幅度从0 %到27 %, 花粉库中的等位基因频率在群体间变化很大(Davidson et al., 1997)。在这种情况下, 基因流通过花粉进行时远非常数。传统模型仅仅考虑了二倍体个体的迁移, 因此, 适合于植物群体的基因种子流, 但不能用于单倍体迁移的花粉流。
其次, 若花粉流和种子流不是很小的话, 在经典模型公式中的迁移率, 不能简单地用种子和花粉流进行线性替代。花粉流的实现是通过与子房结合产生种子后进行的, 因此受交配系统影响。若迁移率不是太小, 如从邻近群体来的迁移, 花粉与种子流的交互作用将会影响群体结构, 这种交互作用类似于位点间的“上位性”效应。若交配系统远离随机交配的话, 这种效应将会变得明显, 然而若花粉和种子迁移率都很小时, 经典公式中的迁移率用花粉和种子迁移率的线性替代是可行的(Ennos, 1994)。
第三, 植物3种基因组的群体遗传结构是不同的。3个不同的基因组(核DNA, 叶绿体和线粒体DNA)有不同的遗传方式(Mogensen, 1996)。例如大多数针叶树如火炬松(Neale et al., 1989)和落叶松(Szmidt et al., 1987; DeVerno et al., 1993), 核DNA, 叶绿体DNA及线粒体DNA依次表现为双亲父本和母本遗传。不同的遗传方式影响其基因的迁移机制, 对于父本和双亲遗传的基因, 迁移可通过种子和花粉两种途径进行, 而对于母本遗传基因, 迁移只有通过种子流才能实现。理论结果证明在一定的条件下, 双亲遗传基因的群体遗传分化最小, 其次为父本遗传基因, 最大的为母本遗传基因(Petit et al., 1993; Ennos, 1994; Hu et al., 1997)。利用核和细胞器基因标记来研究群体分化, 可以估计花粉与种子流的相对贡献(Ennos, 1994; McCauley, 1995)。这点从适合于动物群体的模型中是不可能获得的。
第四, 3个不同基因组上的基因群体结构差异提供了估计花粉和种子流, 推测群体形成历史和路径等信息。细胞核质基因相互关系有助于深入洞察群体结构, 花粉流和种子流可以影响细胞核质交互作用(Asmussen et al., 1991)。Asmussen等(1989)研究了在杂交区内非随机交配和迁移对细胞核质关系的动态影响, 理论上证明在杂交区内连续的迁移可产生永久的细胞核质基因间不平衡, 因此, 核与细胞质基因频率数据可以用于杂交区内基因流的估计。
在亚群体间发生高频率“翻转(turnover)”现象的区型群体中, 群体结构常受“奠基者效应(founder effect)”及种子和花粉的影响, 因3种不同遗传方式基因的巨型群体结构可以不同(McCauley, 1975), 这种差异与群体建立历史是相联的。如果分别考虑植物3个基因组并假设花粉与子房随机结合(随机交配)的话, 它们之间群体分化差异可以用来推测群体的形成历史。例如Le Corre等(1997a; b)和JΦhnk等(1997)应用同功酶和叶绿体DNA标记分别研究了柄叶栎(Quercus petraea), 树种在全自然分布区域和在丹麦境内冰期后的迁移形成历史。因此植物细胞核质基因互作研究在今后有可能成为重要的研究领域。理解这种交互作用有助于在更深层次上理解群体遗传结构。
7 小结一个种的空间分布形成机制是非常复杂的, 如何理解这种机制对于揭示现实的自然群体结构是非常重要的, 直到现在主要使用3个经典模型及其异体来模拟自然群体遗传结构, 用岛屿和步石模型来描述离散分布群体, 用距离隔离模型来描述连续分布群体。应用这些模型, 一些有关群体结构信息可以获得估计, 然而也须知道有许多假设条件隐含在这些模型中, 暗示这些模型与现实群体的差距, 其中一个重要的急需开发的研究领域就是研制适合于植物, 尤其是林木树种的群体遗传结构理论, 对此本文进行了详细阐述。
Asmussen M A, Schnabel A. 1991. Comparative effects of pollen and seed migration on the cytonuclear structure of plant populations I. Maternal cytoplasmic inheritance.Genetics, 128: 639-654. |
Asmussen M A, Arnold J, Avise J C. 1989. The effects of assortative mating and migration on cytonuclear associations in hybrid zones. Genetics, 122: 923-934. |
Avise J C. 1994. Molecular markers, natural history and evolution. London: Chapman and Hall.
|
Barbujani G. 1987. Autocorrelation of gene frequencies under isolation by distance. Genetics, 117: 777-782. |
Barton N H. 1979. Gene flow past a cline. Heredity, 43: 333-339. DOI:10.1038/hdy.1979.86 |
Barton N H. 1983. Multilocus clines. Evolution, 37: 454-471. DOI:10.1111/j.1558-5646.1983.tb05563.x |
Barton N H, Hewitt G M. 1989. Adaptation, speciation and hybrid zones. Nature, 341: 497-503. DOI:10.1038/341497a0 |
Barton N H, Wilson I. 1995. Genealogies and geography. Philosophical Transactions of the Royal Society of London Series B Biological Sciences, 349: 49-59. DOI:10.1098/rstb.1995.0090 |
Birky C W.Evolution and variation in plant chloroplast and mitochondrial genomes.In: Gottlieb L D, Jain S K et al.Plant Evolutionary Biology.New York: Chapman and Hall, 1988, 23~ 53
|
Crow J F, Aoki K. 1984. Group selection for a polygenic behavioral trait:Estimating the degree of population subdivision. Proceedings of the National Academy of Sciences USA, 81: 6073-6077. DOI:10.1073/pnas.81.19.6073 |
Davidson R, EI-Kassaby Y A. 1997. Genetic diversity and gene conservation of pacific silver fir (Abies amabilis)on vancouver island, British Columbia. Forest Genetics, 4: 85-98. |
DeVerno L L, Charest P J, Bonen L. 1993. Inheritance of mitochondrial DNA in the conifer Larix. Theoretical and Applied Genetics, 86: 383-388. |
Dumolin-Lapegue S, Pemonge M H, Petit R J. 1997. An enlarged set of consensus primers for the study of organelle DNA in plants. Molecular Ecology, 6: 393-397. DOI:10.1046/j.1365-294X.1997.00193.x |
Endler J A.Geographic variation, speciation, and clines.In: May R M (ed).M onographs in population biology.Princeton.N J: Princeton University Press, 1997
|
Ennos R A. 1994. Estimating the relative rates of pollen and seed migration among plant populations. Heredity, 72: 250-259. DOI:10.1038/hdy.1994.35 |
Falconer D S.Introduction to quantitative genetics.third edition, Longman, 1989
|
Felsenstein J. 1975. Genetic drift in clines which are maintained by migration and natural selection. Genetics, 81: 191-207. |
Felsenstein J. 1975. A pain in the torus:some difficulties with the model of isolation by distance. American Naturalist, 109: 359-368. DOI:10.1086/283003 |
Fisher R A. 1937. The wave of advance of advantageous genes. Annals of Eugenics, 7: 355-369. DOI:10.1111/j.1469-1809.1937.tb02153.x |
Fisher R A. 1950. Gene frequencies in a cline determined by selection and diffusion. Biometrics, 6: 353-361. DOI:10.2307/3001780 |
Gaggiotti Q E, Smouse P E. 1996. Stochastic migration and maintenance of genetic variation in sink populations. American Naturalist, 147: 919-945. DOI:10.1086/285886 |
Gilpin M E. 1991. The genetic effective size of a metapopulation. Biological Journal of the Linnean Society, 42: 165-175. DOI:10.1111/j.1095-8312.1991.tb00558.x |
Hadrys H, Balick M, Schierwater B. 1992. Application of random amplified polymorphic DNA(RAPD)in molecular ecology. Molecular Ecology, 1: 55-63. DOI:10.1111/j.1365-294X.1992.tb00155.x |
Haldane J B S. 1948. The theory of a cline. Journal of Genetics, 48: 277-284. DOI:10.1007/BF02986626 |
Hanski I, Gilpin M. 1991. Meatpopulation dynamics:a brief history and conceptual domain. Biological Journal of Linnean Society, 42: 3-16. DOI:10.1111/j.1095-8312.1991.tb00548.x |
Hanski I. 1994. Patch-occupancy dynamics in fragmented landscapes. Trends in Ecology and Evolution, 9: 131-135. DOI:10.1016/0169-5347(94)90177-5 |
Hansson L. 1991. Dispersal and connectivity in metapopulations. Biological Journal of Linnean Society, 42: 99-103. |
Hu X S, Ennos R A. 1907. On estimation of the ratio of pollen to seed flow among plant populations. Heredity, 79: 541-552. |
JΦhnk N, Siegismund H R. 1997. Population structure and post-glacial migration routes of Quercus robur and Quercus petraea in Denmark, based on chloroplast DNA analysis. Scandinavian Journal of Forest Research, 12: 130-137. DOI:10.1080/02827589709355394 |
Kimura M. 1953. Stepping-stone model of population. Annual Report of National institute of Genetic, 3: 62-63. |
Kimura M, Weiss G H. 1964. The stepping stone model of population structure and the decrease of genetic correlation with distance. Genetics, 49: 561-576. |
Le Corre, Machon N, Petit R J, et al. 1997a. Colonization with long-distance seed dispersal and genetic structure of maternally inherited genes in forest trees:a simulation study. Genetic Research, 69: 117-125. DOI:10.1017/S0016672397002668 |
Le Corre, Dumolin-Lapegue V S, Kremer A. 1997b. Genetic variation at allozyme and RAPD loci in sessile oak Quercus petraea (Mattt.)Liebl.:the role of history and geography. Molecular Ecology, 6: 519-529. DOI:10.1046/j.1365-294X.1997.00214.x |
Levins R. 1970. Extinction. American Mathematics Society, 2: 75-108. |
Li C C. 1976. First Course in Population Genetics. Pacific grove, California: The Boxwood Press.
|
Maruyama T. 1970. Effective number of alleles in a subdivided population. Theoretical Population Biology, 1: 273-306. DOI:10.1016/0040-5809(70)90047-X |
Maruyama T, Kimura M. 1980. Genetic variability and effective population size when local extinction and recolonization of subpopulations are frequent. Proceedings of the National Academy of Sciences USA, 77: 6710-6714. DOI:10.1073/pnas.77.11.6710 |
Malécot G.Les mathematiques de l' heredite.Masson, Paris, 1948
|
Malécot G.The mathematics of heredity.Yermanos D M.Freeman, San Francisco, 1969
|
Mallet J.The genetics of biological diversity : from varieties to species.In: Gaston K J(ed).Biodiversity: A biology of numbers and difference.Blackwell Science Ltd, 1996, 13~ 53
|
McCauley D E. 1995. The use of chloroplast DNA polymorphism in studies of gene flow in plants. Trends in Ecology and Evolution, 10: 198-202. DOI:10.1016/S0169-5347(00)89052-7 |
Millar C I. 1983. A step cline in Pinus muricata. Evolution, 37: 311-319. DOI:10.1111/j.1558-5646.1983.tb05541.x |
Morgante M, Olivieri A M. 1993. PCR-amplifed microsatellites as markers in plant genetics. Plant Journal, 3: 175-182. DOI:10.1111/j.1365-313X.1993.tb00020.x |
Mogensen H L. 1996. The hows and whys of cytoplasmic inheritance in seed plants. American Journal of Botany, 83: 383-404. DOI:10.1002/j.1537-2197.1996.tb12718.x |
Mullis K, Faloona F, Scharf S, et al. 1986. Specific enzymatic amplification of DNA in vitro:the polymerase chain reaction. Cold Spring Harbour Symposia on Quantitative Biology, LI: 263-274. |
Nagylaki T. 1975. Conditions for the extence of clines. Genetics, 80: 595-615. |
Nagylaki T. 1976. Clines with variable migration. Genetics, 83: 867-886. |
Nagylaki T. 1978a. Random genetic drift in a cline. Proceedings of the National Academy of Sciences USA, 75: 423-426. DOI:10.1073/pnas.75.1.423 |
Nagylaki T. 1978b. Clines with asymmetric migration. Genetics, 88: 813-827. |
Nagylaki T. 1979. The island model with stochastic migration. Genetics, 91: 163-176. |
Nagylaki T. 1983. The robustness of neutral models of geographical variation. Theoretical Population Biology, 24: 268-294. DOI:10.1016/0040-5809(83)90029-1 |
Neale D B, Sederoff R R. 1989. Paternal inheritance of chloroplast DNA and maternal inheritance of mitochondrial DNA in loblolly pine. Theoretical and Applied Genetics, 77: 212-216. DOI:10.1007/BF00266189 |
Nei M. 1975. Molecular population genetics and evolution. New York: North Holland and American Elsevier.
|
Nei M, Takahata N. 1993. Effective population size, genetic diversity, and coalescence time in subdivided populations. Journal of Molecular Evolution, 37: 240-244. |
Petit R J, Kremer A, Wagner D B. 1993. Finite island model for organelle and nuclear genes in plants. Heredity, 71: 630-640. DOI:10.1038/hdy.1993.188 |
Rafaalski J A, Tingey S V. 1993. Genetic diagnostics in plant breeding:RAPDs, microsatellites and machines. Trends in Genetics, 9: 275-280. DOI:10.1016/0168-9525(93)90013-8 |
Rannala B, Hartigan J A. 1995. Identity by descent in island-mainland populations. Genetics, 139: 429-437. |
Slatkin M, Maddison W P. 1990. Detecting isolation by distance using phylogenies of genes. Genetics, 126: 249-260. |
Slatkin M. 1973. Gene flow and selection in a cline. Genetics, 75: 733-756. |
Slatkin M, Maruyama T. 1975. Genetic drift in a cline. Genetics, 81: 209-222. |
Slatkin M. 1987. Gene flow and geographic structure of natural population. Science, 236: 787-792. DOI:10.1126/science.3576198 |
Sokal R R, Oden N L. 1978a. Spatial autocorrelation in biology 1.Methodology. Biological Journal of the Linnean Society, 10: 199-228. DOI:10.1111/j.1095-8312.1978.tb00013.x |
Sokal R R, Oden N L. 1978b. Spatial autocorrelation in biology 2.Some biological implications and four applications of evolutionary and ecological interest. Biological Journal of the Linnean Society, 10: 229-248. DOI:10.1111/j.1095-8312.1978.tb00014.x |
Sokal R R. 1979. Testing statistical significance of geographical variation patterns. Systematic Zoology, 28: 227-232. |
Strand A E, Leebens-Mack J, Millgan B G. 1997. Nuclear DNA-based markers for plant evolutionary biology. Molecular Ecology, 6: 113-118. DOI:10.1046/j.1365-294X.1997.00153.x |
Szmidt A E, Alden T, Hallgren J E. 1987. Paternal inheritance of chloroplast DNA in Larix. Plant Molecular Biology, 9: 59-64. DOI:10.1007/BF00017987 |
Takahata N. 1983. Gene identity and genetic differentiation of populations in the finite island model. Genetics, 104: 497-512. |
Takahata N, Nei M. 1984. Fst and Gst statistics in the finite island model. Genetics, 107: 501-504. |
Wade M J, McCauley D E. 1988. Extinction and recolonization:their effects on the genetic differentiation of local populations. Evolution, 42: 995-1005. DOI:10.1111/j.1558-5646.1988.tb02518.x |
Weiss G M, Kimura M. 1965. A mathematical analysis of the stepping stone model of genetic correlation. Journal of Applied Probability, 2: 129-149. DOI:10.2307/3211879 |
White T J. 1996. The future of PCR technology :diversification of technologies and applications. Trends in Biotechnology, 14: 478-483. DOI:10.1016/S0167-7799(96)10068-8 |
Whitlock M C. 1992. Temporal fluctuation in demographic parameters and the genetic variance among populations. Evolution, 46: 608-615. DOI:10.1111/j.1558-5646.1992.tb02069.x |
Wright S. 1921. Systems of mating. Genetics, 6: 111-178. |
Wright S. 1931. Evolution in Mendelian populations. Genetics, 16: 97-159. |
Wright S. 1940. Breeding structure of populations in realtion to speciation. Ammican Naturalist, 74: 232-248. DOI:10.1086/280891 |
Wright S. 1943. Isolation by distance. Genetics, 28: 114-138. |
Wright S. 1946. Isolation by distance under diverse systems of mating. Genetics, 31: 39-59. |
Wright S. 1951. The genetic structure of populations. Annals of Eugenics, 15: 323-354. |
Wright S. 1969. Evolution and the genetics of populations, Vol 2. Chicago: The University of Chicago Press.
|
Wright S. 1978. Evolution and the genetics of populations, Vol 4.Variability within and among natural populations. Chicago: The University of Chicago Press.
|
Young N D. 1996. Concordance and discordance :A tale of two hybrid zones in the Pacific Coast irises(Iridaceae). American Journal of Botany, 83: 1623-1629. DOI:10.1002/j.1537-2197.1996.tb12820.x |
 2002, Vol. 38
2002, Vol. 38

