自然界是宇宙万物的总称, 是各种物质系统相互作用相互联系的整体, 呈现在人们面前是千变万化、广阔无垠、奥妙无穷的物质世界。人类在认识自然的过程中, 正在一层层揭去其面纱, 不断走向深入, 展示其真面目。随着牛顿经典力学的创立, 爱因斯坦相对论, 以及量子力学的发展, 人类在自然科学方面已经取得了辉煌的成就; 随着大气物理学以及其他相关学科的迅速发展, 人类已经登上月球, 进入太空; 人类对微观世界由质点组成的简单系统的运动规律也有了全面而正确的认识(刘式达, 1997)。

但是, 在我们的周围, 象天空中云、弯曲的河流、地球的表面、人肺内膜等, 都是非线性不可逆现象, 而且在自然界中大量存在, 人们往往对这些现象所知甚少, 有许多问题甚至束手无策。1967年Mandelbrot先生在美国《科学》杂志上首次发表一篇题为“英国海岸线有多长?”的论文, 揭开了多年难以解释的问题, 使整个学术界大为震惊。自然界中大部分物体不是有序的、稳定的、平衡的和确定性的, 而是处于无序的、不稳定的、非平衡的和随机的状态之中, 处于非线性过程。在非线性世界里, 随机性和复杂性是其主要特征, 用经典的欧氏几何理论来描述和解释非常困难。分形理论使人们能以新的观念、新的手段来处理这些难题, 透过无序的混乱现象和不规则的状态, 揭示隐藏在复杂现象背后的规律、局部和整体之间的本质联系, 具有广阔的应用前景(张济忠, 1997)。

1 分形基本理论 1.1 分形的概念

“分形”这个名词是由哈佛大学数学系教授曼德勃罗特(Mandelbrot)在1975年首次提出的, 其原义是“不规则的、分数的、支离破碎的”物体, 这个名词是参考了拉丁文fractus (弄碎的)后造出来的, 它既是英文又是法文, 既是名词又是形容词, 1977年, 他出版了第一本著作“分形:形态, 偶然性和维数(Fracta1:Form, Chance and Dimension) ”, 标志着分形理论的正式诞生。5年后, 他出版了著名的专著“自然界的分形几何学(The Fractal Geometry of Nature) ”, 至此, 分形理论初步形成。它是揭示自然界非线性系统中有序与无序的统一, 确定性与不确定性的统一。一般地, 可把分形看作大小碎片聚集的状态, 是没有特定长度的图形和构造以及规律的总称。

1.2 分形维数及其测定

设有一条长度为L的线段, 如果用一条长为r的“尺”作为基本单位去测量它, 那么测量的结果是N, 我们就说这条线段有“尺”。显然N的数值与所用的“尺”的大小有关, 它们之间的关系是N (r) =A/r²~r²。同理, 如果测量的是一块面积为A的平面, 这时就用边长为r的小正方形去测量它, 才能得到确定的N值, 其值为N (r) =A/r²~r²。r越小, 测得越准, 所需要小方块的数目总是比例于A/r²。如果不是用小方块去测量, 而仅用长为r的“尺”去直接测量, 那是测量不出这块面积的大小的。由此可见, 测量任何一个物体必须用适合于它的“尺”去测量, 才能给出正确的数值。同样可以用半径为r的小球来填满一块体积V, 所需小球数目比例于V/r³。数学家们把这个事实归结为下述结论:对于任何一个有确定维数的几何体, 如果用与它相同维数的“尺”去量度, 则可以得到一确定的数值N; 若用低于它的维数的“尺”去量它, 结果为无穷大, 若用高于它维数的“尺”, 结果为零。其数学表达式为

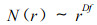
对上式两边取自然对数, 再进行简单运算后, 可得下式:

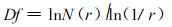
式中, Df就称为Hansdorff维数。它可以是整数, 也可以是分数。在欧氏几何学中所讨论的几何体, 是光滑平整的, 其Df值为1, 或2, 或3, 均为整数。但自然界中的各种物体, 其形态都是千奇百怪, 并不都是光滑平整的, 如弯弯曲曲的海岸线, 人肺的内膜, 线粒体的内表面, 森林的边界线, 树木冠型, 树叶的形状, 农作物根系的形态等等, 如何确定这些不规则、不平整物体的维数呢?数学家们为此设想了许多病态的几何图形, 如Koch曲线就是一个例子, 可以用它来模拟自然界中的海岸线。应用上述的公式可以求出Koch曲线的维数, 其基本单元由4段等长的线段构成, 每段等长度为18, 即N=4, r=1/3,

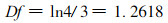
Df是个比1大的分数, 这反映了Koch曲线要比一般的曲线来得复杂和不规则, 它是一条处处连续但不可微的曲线。人们常把Hausdorff维数是分数的物体称为分形, 把此时的Df值称为该分形的分形维数, 简称分维, 也有人把该维数称之为分数维数。在确定一个物体是否是分形时, 除了看其Hausdorff维数值以外, 还必须看其是否具有自相似性和标度不变性。

综上所述可以发现, 那些至今为止认为异常的分形集在某种意义上说应该是规则的, 被认为是病态的结构应该自然而然地从非常具体的问题中演化出来。分形计划可以用来描述自然物体的复杂性, 不管其构造如何, 所有的分形都有一个重要的特征, 可通过一个特征数, 即分形维数测定其不平度、复杂性或卷积度。对分形几何的这一表征并不只限于包含在某一平面之内的数学图形或形态, 人们还能计算出诸如河流、海岸线、树木、闪电、云层、血管、神经网络等之类真实物体的分形维数, 例如, 人的血管动脉分形维数大约在2.7;按理查森(Richardson L F)经验公式挪威海岸线的分形维数应为D=1.52。不独挪威海岸线是这样, 其它国家海岸线也是分形(分形维数值可能不同)。自然界就是如此的奥妙无穷, 正如Mandelbrot所指出的:“云团不是云团, 山岳不是锥体, 海岸线不是圆, 树皮不是光滑的, 闪电不是沿直线传播的”。

1.3 分形理论与木材科学

分形理论的应用近年国内发展较快, 特别在材料方面(张济忠, 1997); 林业唯有综述介绍外(陈华豪, 1992), 具体应用还不多见(马克明, 1997), 国外的报道较多(Zeide, 1991); 分形理论在木材方面的应用研究始于20世纪90年代(Hatzikiriakos, 1994; Fan, 1995; Jose et al., 1997), 主要是对木材表面和水进入木材过程的分析。我国这方面研究到目前为止还没有开始, 作者就分形理论在木材科学中的应用曾发表综述(费本华, 1999), 并摸索分形理论在木材科学中的具体应用。对于任何一种材料, 为了合理的高效的利用它, 必须全面地了解它的特性。木材作为一种天然高分子材料, 更是如此。木材的形成机理、复杂的细胞结构、物理力学性质等还存在许多难以解释问题, 它的各向异性、变异性等给进一步认识带来不便。多年来, 木材科学家在该领域中积累了大量经验, 在方法和手段上达到一定的高度, 成果卓著。分形理论在木材科学中的应用刚刚开始, 但从分形和木材两者的特点来看, 如果能有机地结合, 会使木材科学有新的突破。

2 研究方法 2.1 试材采集

实验用试材采自江苏省泰州姜堰市境内。泰州地区是我国银杏中心产区之一, 有悠久的栽培历史。在姜堰市林业技术推广中心的协助下, 选择标准木3株, 每株取1.3m高处40cm厚圆盘作为分析样品带回。采样地点为实生苗造林, 土壤黄棕壤, 土层深厚, 生长环境人为破坏性小。试材采集野外记录见下表。板栗木材采自安徽滁县(记录略)。

2.2 试样制作

将采回的样品气干一段时间后, 锯解成20cm厚的圆盘两块, 其中一块用于分形实验。将用于分形实验的试材剔除小部分心材和边材, 然后按照5mm、10mm、15mm……50mm、55mm的边长随机制取立方体, 每个规格立方体做3个重复, 制作误差不超过0.5mm。板栗试材制作与前相同。

2.3 试验方法

将制作好的试样量取初始重量和尺寸。称重是在万分之一电子天平上进行, 尺寸测量是用螺旋测微尺量取, 室内温度5℃。然后将准备好的试样分别放入烘箱中, 按照20℃、40℃、60℃、80℃和100℃的不同温度段, 进行连续升温处理, 每次改变温度的时间间隔为4h, 每次改变温度前量取尺寸和重量。将获得的实验数据, 按照分形理论的分析方法处理和分析。

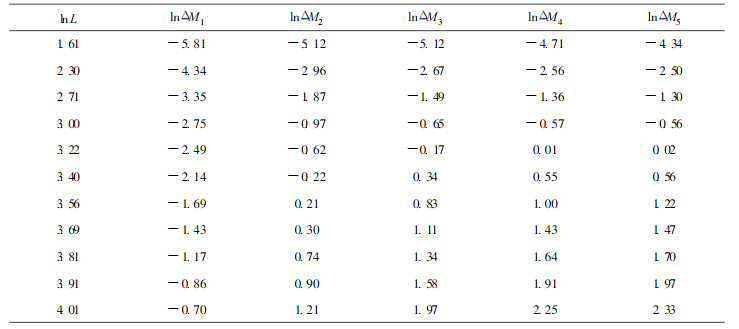
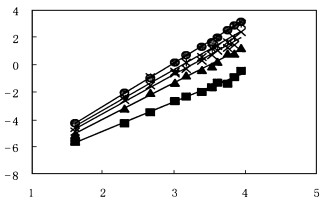
3 结果与分析

将银杏木材随温度变化各阶段的重量列于表 2, 由表 2可以看出, 不同尺寸试样随温度升高重量的变化情况。不同温度重量与初重的差值列于表 3, lnΔM为重量变化值的对数。由表 3作图 1, 得银杏木材在不同温度下的对数曲线, 图 1中各点近于直线, 因此用直线拟合, 图中每条直线lnΔM_l至lnΔM₅分别表示温度20℃至100℃状态下银杏木材中水分的移动状况, 直线的斜率即表示分形维数。由图中lnΔM_l至lnΔM₅可以明显看出, 直线的斜率逐渐增大, 这表明随着温度的升高, 分形维数逐渐增大, 换言之, 根据分形维数可以描述木材的干缩程度和空隙度。

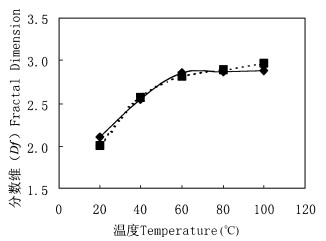
用同样方法测得板栗木材的分形维数。将两树种木材的分形维数值建立图 2。由图 2可以看出, 随着温度的升高, 分形维数值逐渐增大, 其数值逼近于3, 而不超过3, 因为3维空间分形维数值在2至3的范围。随着温度的增加, 木材细胞中的水分逐渐逸出, 开始是胞腔水, 接着是胞壁水, 纤维之间的水分、微孔中的水分等, 由简单到复杂。图中银杏木材孔隙空间分维数增加到一定程度趋于平稳, 这可能是温度升高到一定程度, 木材中的水分已基本逸出, 说明木材孔隙空间分维趋于稳定。

在木材科学中, 象木材空隙度、木材比重等与木材体积有关方面情况, 还比较多, 木材空体积和实体积的研究一直是个复杂课题, 过去在范围上和程度上难以描述。本研究通过实验表明, 木材的内部空体积与木材立方体的尺寸大小之间, 可由分形维数来描述其变化规律。木材微观构造的分析, 细胞生长的分析(Marcelo, 1995), 也可以应用这种方法。

4 结论

该研究的目的是探讨木材内部空间是否可以通过分形进行描述。通过一个简单而可靠的木材干缩实验, 讨论木材内部孔隙空间的复杂性。结果表明, 可以通过木材干缩过程, 用分形维数来描述木材孔隙空间的特征, 这在木材科学方面国际上尚属首次。随着温度的增加, 木材的分形维数也呈增加趋势, 描述了木材水分自内部空间逸出的过程和规律性, 分形维数逼近于3, 反映出木材结构的复杂性。本研究只是通过一个干缩实验得到的结果, 还可以在其他方面进行扩大应用, 如木材的微观结构、细胞的生长、复合材料内部空间的分析, 木材表面花纹, 木材表面的粗糙度等。该理论的应用, 有可能在木材科学的应用研究中有新的突破。