文章信息
- 陈辉.
- Chen Hui.
- 锥栗人工林营养综合指标诊断研究
- A STUDY ON NUTRIENT DIAGNOSIS OF CASTANEA HENRYI PLANTATION BY SYNTHETIC INDICES
- 林业科学, 2001, 37(专刊1): 52-59.
- Scientia Silvae Sinicae, 2001, 37(专刊1): 52-59.
-
文章历史
- 收稿日期:2001-01-08
-
作者相关文章
营养诊断是决定施肥方案的基础。只有在诊断的基础上,结合施肥措施研究施肥与产量的关系,并使两者统一起来,才能使施肥具有效性,经济性和科学性,从而为林木营养管理提供实践指导和理论依据。营养诊断根据其对象和诊断的目的,可采用的方法主要有形态诊断法、养分含量临界值法、土壤分析法和综合诊断法等。从近年来这方面的研究进展看来,结合土壤分析和植株分析的方法被较多地采用(李贻铨,1991;姜远茂,1995;胡芳名,1991;陈道东,1991;赵明范,1991;卫茂荣,1994;Beaufils,1973;Fallahi et al.,1984; Davee,1986;Walworth,1986;Parent,1989;Goh,1992)。而运用综合诊断分析法(DRIS)能较全面地评价树体的各养分及其比例,以及确定这种比例的合理范围,避免由仅凭某一(或几个)元素含量的高低作出丰缺判断的片面性。但影响产量的营养组成及平衡是非常复杂的,既有不同的元素及含量的影响,又有这些元素之间相互比例是否平衡的影响,使得数据分析变得复杂。不同的营养元素从不同的角度说明了树体的养分状况,能否设计出一个综合指标,它一般地表示树体的营养水平,这样既可简化数据,又可以体现树体营养的内在规律,值得深入研究。陈道东(1991),在其研究的结论中讨论到了用叶片综合指标代表叶片养分状况的可能性;卜兆宏(1982)在土壤分类研究中试用了这一方法,但在林木叶片营养诊断中尚未见相关研究的报道。锥栗人工林是一种重要的经济林,其树体营养是否平衡是产量形成的关键,但其营养诊断未见报道(陈辉等,1999a;1999b;2000)。建立在主分量分析基础上的综合指标分析就是一种把原来多个指标化为少数几个相互独立的综合指标的分析方法,本研究首次尝试将这种方法应用于锥栗人工林的营养诊断。
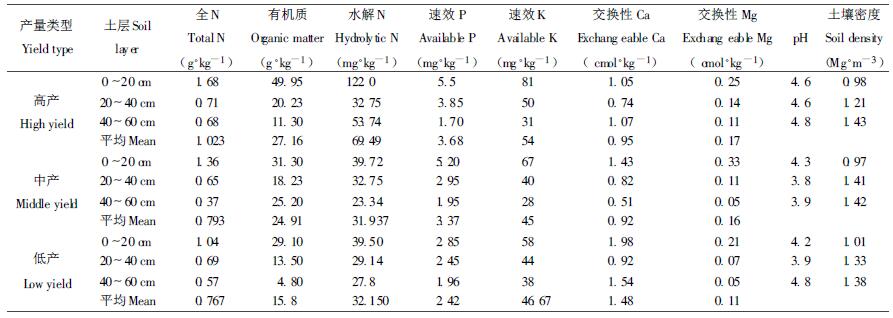
1 材料和方法于建瓯水源乡,在锥栗人工林几年低改措施的基础上,经过详细调查后,选择经营好,采用施肥和土壤管理措施,产量较高的林分1块及与其林分年龄相同(8 a生)产量差异明显的另外2块锥栗人工林分,品种为嫁接后的黄榛,3块林分坡向均为东南,坡度分别在10°~17°之间。根据产量表现,在每块林分中分别选择60株,通过每株产量实测结果,合并3个林分数据计算出平均单株产量为
|
|
|
|
根据主分量分析的要求(唐守正,1986; 张尧庭,1980),将不同产量类型林分叶片养分测定结果计算其平均值向量(N、P、K、Ca、Mg)=(1.7366,0.1159,0.4594,0.6436,0.2341)和标准差向量(N、P、K、Ca、Mg)=(0.1559,0.0109,0.0861,0.0271,0.0126)。各元素间的相关系数矩阵为:
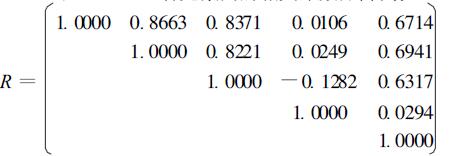
|
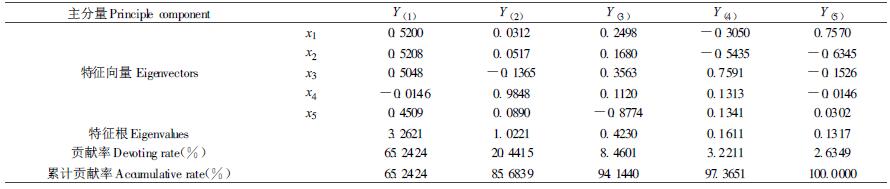
从各元素相关系数可知,N、P、K、Mg之间的相关性较大,而Ca与4种元素间的相关性不大,即Ca对于产量大小的影响较为次要。主分量分析的重要内容是计算各特征向量和特征根及其各主分量的贡献率和累计贡献量(表 3),依据特征根的大小及累计贡献率选取能综合反应数据信息的主分量,使得分析更为简单明了。
|
|
从表 3知,最大特征根λ1=3.2621,对应的第1主分量贡献率达65.2424%,其特征向量中,x1、x2、x3、x5相差不大,它们分别表示N、P、K、Mg 4个因子,而x4系数很小,它表示Ca因素的影响较小。第2大特征根为1.0221,在第2主分量的5个特征向量中,x4系数最大,它主要表示Ca元素的影响。前两个主分量的累积贡献率达到85.6839%,为了简化分析,从而达到在较低维空间近似表示样本点的目的,当累积贡献率大于0.8或0.85时,可以将余下的主分量舍去(唐守正,1986)。因此,选择前两个主分量作进一步分析,以便于在2维平面上对综合指标作直观比较。
因子负荷量是主分量Y(K)与原分量xj的相关系数,也称第j因子在第K个主分量上的负荷量,它反映原变量与主分量之间的关系,几何解释为原坐标轴上单位长度在某个主坐标轴上投影的长度,计算得到各因子负荷量(表 4)。
|
|
各因子负荷量计算表明:第1主分量与x1、x2、x3、x5这4个因子的(即N、P、K、Mg)的相关关系很紧密,而与x4的相关性很小(即Ca),说明第1主分量主要反映了这4种因素的综合影响;第2主分量仅与x4的相关性紧密,它主要反映x4的影响,其余主分量与各因子的相关性均较小,可考虑舍去这些主分量。
根据以上计算分析,可以认为选择前两个主分量能够基本表达原数据的大部分信息。为了对所调查测定的锥栗叶片养分作出诊断分析,将各样株叶片的养分实测值,代入选择的两个主分量方程可得到各样株的主分量坐标(计算结果略),按各点主分量坐标值将各点位置确定在主分量坐标图上(图 1),就能很直观地表现出这些植株个体叶片营养间的相互关系。由图(图 1)可见,全部90株叶分析值可以大致分为两组,中间可由虚线隔开,位于虚线下侧的是实测高产量类型的样株,而虚线上方的样株基本上是中、低产林分的样株。
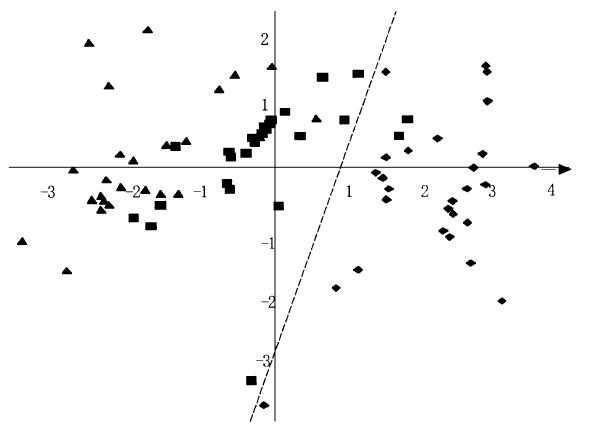
|
图 1 各产量类型叶片养分元素的主成份坐标图 Fig. 1 Coordinate figure of principle component about nutrient elements in leaves of each yield type ◆高产High-yield;■中产Middle-yield;▲低产Low-yield. |
显然,各主分量坐标是由原变量经主分量方程求得,它是原变量在主分量坐标上的投影。因此,各主分量实质上是经过变换过的能反映原变量变化的综合变量,对于营养诊断而言,它是综合评价样株营养水平的指标。在一般情况下,当因子之间的相关性较强时,总能找到较少的(即低于原变量个数)主分量,以便在较低维数空间分析比较复杂的多因子问题,如果因子之间的相关性很小则主分量分析效率就不高。因为树体营养元素因子之间的相关性总是存在的,因此,主分量分析很适用于解决这类问题。在运用时与其它诊断方法一样,首先必须根据不同产量水平叶片养分含量值,经主分量分析后,确定各特征根、特征向量值,并根据累计贡献率确定选取的主分量个数。将原始变量各值代入相应的主分量方程,求得各点原始变量的主坐标值,为了直接比较,在主坐标图形表达的基础上,能够区分各不同产量水平树体叶片养分的含量值。由图 1可知,如果图中的虚线作为阈值,可为叶片养分含量及其是否平衡作出诊断。因此,图中虚线的确定就成为诊断分析不可缺少的依据。由多元统计学原理可知,该虚线可用各元素的某种线性组合函数表示,各点坐标可通过与这一函数值的比较,判定其所处的区域,从而达到判别诊断分析的目的。
为此,介绍判别诊断分析的基本思想(唐守正,1986)如何求算这一线性组合函数。先从2级判别诊断分析入手,当系统的产量只作高产和低产两种状态来区别时,通过对不同产量类型叶片分析值数据,从前面的分析可以知高产类型和低产类型(包括中产类型)基本上可用一条直线将其分成两部分,位于一侧的点是高产类型,位于另一侧的点是中、低产类型。假设该直线用L表示,L=C0+C1x1+C2x2则C0+C1x1+C2x2>0或C1x1+C2x2>-C0为中产或低产,或C0+C1x1+C2x2<0或C1x1+C2x2<-C0为高产。如果能够求出这条直线方程即可解决林分叶片分析值及其产量类型的诊断判别,即C1x1+C2x2可作为判别x1、x2为不同水平产量类型的函数(注:如果根据前面的分析这里的x1、x2则分别对应于前面各点的主分量值Y(1)、Y(2),为表达上的方便,这里采用x1、x2表述),其中-C0是判别的准则。令Y=C1x1+C2x2,称之为判别函数。令yc=C0称之为判据。因此,判别诊断分析的关键就是根据什么原则处理所占有的数据和怎样求算C0、C1和C2。在一般情形下,影响产量的营养因素较多,为了研究这些因素对产量的影响,就必须拟定一个综合指标,借助于它把各因素统一起来。
设影响产量的营养因素有P个,则对产量的综合评价指标可表示为:
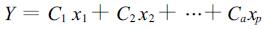
|
如果只考虑两种产量状态即高产和低产,可将其分为2类,分别记为A类和B类。A类的综合评价指标以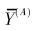
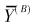
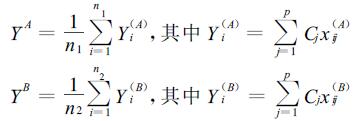
|
从两组的综合评价指标来看,如果两组指标的差距越大则越易诊断;同时如果组内综合评价指标差距越小,说明它们越集中在均值附近,也有利于判别。因此,根据费雪准则有:
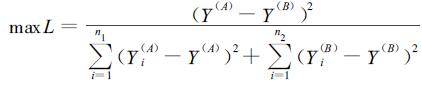
|
因为L是Cj的函数,故有当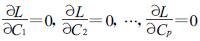
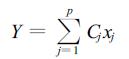
|
判据的确定是以A类和B类数据量的大小为权数,计算其综合评价指标的加权平均数Yc作为判据: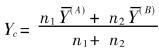

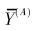
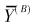
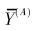
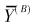
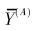
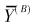
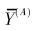
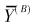
这样就解决了诊断判别综合指标的确定问题,即前面分析所提到的诊断判别的阈值确定。讨论到更为一般的情形,即如果产量类型不仅仅分为两类时,可按上述方法先分为两类,再由分出的类中划分新类,作逐级判别等等。应用各产量类型叶片分析的数据,以下建立诊断判别系统对其进行分析。
2.2 应用综合指标作判别诊断(1) 当考虑将产量分为高产、低产(含中产) 2种类型时的诊断判别分析,依照上面的方法,求得组平均值矩阵。为讨论方便,记各类总体样本平均数为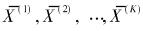

|
其中K为类别数,这里K=2。
高产类 (1.9019 0.1273 0.5778 0.6345 0.2432)
低产类 (1.6535 0.1102 0.4002 0.6481 0.2295)
各类样本的协方差矩阵之和

|
Qi为第i组样本协方差矩阵。
计算矩阵(Q1+Q2) -1·B的前m个特征向量a1,a2,…,am求得λ1=0.9711,λ2=0.0000,λ3=0.0000,λ4=-0.0000,λ5=-0.0000。该矩阵只有一个非零特征根λ1=0.9711,因此其1维判别和多维判别等价(唐守正,1986),选择其相应的特征向量即为判别函数的系数,由计算结果得到。其1维判别函数为:
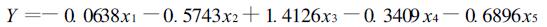
|
各类在判别坐标系中的中心点为
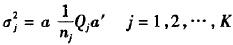
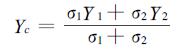
|
应用判别函数和判据Yc就能根据叶片养分测定值对产量类型进行判别。在划分为高、低产两类时,将各样本测定值代入判别函数并与判据比较,得到1维情况的回判结果为第1类共有样本数=30,正判率为100%;第2类共有样本数=60,正判率为100%。
可见上述的诊断判别函数的正判率相当高,可以对各产量类型作出准确的诊断。由于判别诊断分析事先必须对产量的状况及叶片营养含量有所了解,即先把产量类型划分好,然后依据数据建立诊断判别系统,因此,产量类型的划分就非常重要。下面讨论如果将原数据仍分两组,但高产组和中产组分为一类型,低产组自成一类时的诊断判别情况,与前面分析相同,计算得到:

|
特征根:λ1=0.5729,λ2=0.0000,λ3=-0.0000,λ4=-0.0000,λ5=0.0000
1维判别函数为:

|
各类在判别坐标系中的中心为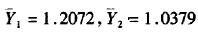
仍用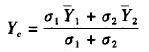
对各样本进行回判算得:第1类样本数=60,正判样本数=53,正判率=88.33%,共有样序号为(25,30,36,42,43,46,50)等7个样点不能正判;第2类样本数=30,正判样本数=26,正判率=86.67%,共有样序号为(66,74,82,87)等4个样点不能正判。
可见,不同的类型划分其诊断判别的准确率有较大差异。从本研究情况来看,如果仅考虑将产量类型划分为两种,则第1种划分方法可以得到极高的正判率,即这种划分所建立的判别诊断系统及其模型是合理的,符合实际情况,能够根据叶片养分分析的结果对其养分是否平衡作出诊断判别,因此,在相似的研究条件下,应对不同的划分方法进行比较分析,使诊断判别的正判率提高,解决实际问题。
(2) 当考虑将产量类型分为高、中、低3种类型时的诊断判别分析:
由于本研究所涉及的产量水平具有3种较明显的类型即高产、中产、低产,能否将这3种不同产量类型通过与其相关的叶片养分分析结果作出正确的诊断判别,并建立一个适合的诊断判别系统。以下对划分为3种类型时的诊断判别方法进行探讨,仿照与上面相似的步骤,应用所建立的判别函数和判据可以对各样本进行判别,在一维情况下的回判结果为:第1类共有样本数=30,正判率为100%;第2类共有样本数=30,正判数为26,正判率为86.7%,共有样本序号(36,41,46,54)等4个样点不能正判;第3类共有样本数=30,正判数为25,正判率为83.33%,共有样本序号(61,76,82,85,89)等5个样点不能正判。
分析可见,当产量类型划分为3类时,采用叶片养分分析值的判别诊断分析仍可以对样本作出较正确的诊断,但除了第1类高类型完全正判外,其它两类尚有部分样点不能正确判断。因此,能否寻找更为理想的诊断模型,提高诊断的准确性,满足诊断实践的需要。注意到当划分为3种产量类型时,计算得到的特征根λ2尚未被引用到诊断中来,因此,在下面讨论引入第2个特征根λ2及相应的特征向量后对诊断准确性的影响,即2维诊断判别。
b2维判别
这里根据前面计算的结果,选取了2个特征根λ1和λ2,其相应的特征向量为a1、a2,得到了2维判别函数:

|
其中Y为原始变量向量(x1,x2,x3,x4,x5) ′y2=a′2Y。令矩阵A=[a1,a2],则上式可表示为

|
其中y是一个2维向量,上式表示将原p维(p=5)空间中的向量y经线性变换A′变成新的2维空间中的点y,同样可以将Gj总体中心
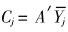


|
显然应将样本Y归于它最近的那个总体,这样得到判别规则如下:
如果d2 (Y,Gl) ≤d2 (Yi,Gj),j=1,2,…,k,则将Y判归Gl类型。
经计算得到对应于λ1和λ2的特征向量方程即判别函数为:

|
通过前面的分析知所有的样本点,都可以经过y1、y2线性变换,转换到y1、y2平面上;同样原来p维坐标系中各产量类型的中心点
同样,在2维判别函数下,对各样本点进行回判,结果为第1类样本数30,正判样本数30,正判率100%;第2类样本数30,正判样本数30,正判率100%;第3类样本数30,正判样本数25,正判率83.33%。
可见,2维判别的效果比一维判别更为理想,第2类样本的正判率也达到了100%,说明了用判别诊断方法可以根据叶片养分测定进行产量类别判别和预测。至此,已完成了不同产量类型叶片测定值的判别诊断分析过程。
3 结论与讨论营养诊断分析的方法较多,但大都有一定的局限性,根据产量与叶片某一定时期内的养分含量存在一定相关的条件下,对产量划分从而进行叶片营养诊断方有意义,但并不是所有的营养元素各自均与产量相关显著,因此,在实践中,首先必须合理地划分产量类型,否则,得不到理想的诊断效果。任一单因素诊断结论可能造成风险,因为仅根据某一元素含量的丰缺下结论未免过于武断,营养元素之间的比例是否协调,在一定条件下,是决定产量的主要因素。
综合指标诊断分析即主分量分析和诊断判别分析,能够较充分利用叶片测定数据的内含信息对营养的平衡与否作出诊断判别,信息内容的提取和分析较全面,不失为诊断判别的一种好方法。本研究尝试性将该方法应用于营养诊断,得到了较满意的结果,不仅可以解决产量高低的判别分析,还可以对不同的产量状态相应的叶分析测定结果进行诊断判别,并作产量预报。比传统的诊断方法更为灵敏,尤其当产量的类型划分较细时,这种方法的作用和优点就会更加突出。判别函数的个数在特征根比较大或至少不为0的情况下会增加诊断判别的准确性,从本研究对3种产量类型的2维判别和1维判别结果可以看到,2维判别在同样条件下诊断判别的正确率要更高,因此,如条件允许,应尽可能增加判别函数的个数,以提高诊断判别的精度。
就一般意义而言,诊断分析是在对产量划分及不同产量类型叶片养分含量的测定结果的基础上进行的,因此产量的划分的正确与合理与否至关重要。在其他条件较一致时高产的林分通常认为其养分代谢是平衡、合理和充分的,因此,将其作为其它产量类型养分丰缺的参比标准。但是,产量究竟达到多大才算高产,即这一比较的标准在实际工作中如何获取?这在园艺与农作物栽培实践中,已得到了一些较成功的经验。但对于锥栗人工林来说,由于其较规范化的栽培研究刚刚开始,只能根据现实条件选取相对表现高产的群体并以其叶分析结果作为比较的标准,这种高产与理论上理想的产量可能存在差异,但从诊断的目的考虑,对制定指导栽培营养管理措施来说,应该是现实和有效的。
任何一种诊断分析方法都不是十分完美的,综合指标诊断判别分析法尽管可以对营养的平衡与否作出判定,也可以用计算机建立诊断判别系统,但在具体分析某一个元素的丰缺时,最好结合DRIS法作进一步分析。由于DRIS法中的指数法便于计算机的运算,因此,随着诊断分析研究的更加深入,可以建立较自动化的综合诊断——综合指标诊断判别系统,提高诊断分析的效率,节约大量的运算分析时间,将结果尽快反馈到栽培实践需要之中。
卜兆宏. 1982. 土壤分类分级中综合数值分析法的初步研究. 土壤学报, 19(3): 283-295. |
陈道东. 1991. 林木叶片最适养分状态的模拟诊断. 林业科学, 27(1): 1-7. |
陈辉, 何方. 1999a. 锥栗人工林生态系统养分特征和生物循环的研究. 林业科学, 35(6): 19-27. |
陈辉, 何方. 1999b. 锥栗人工林生态系统能量特征研究. 江西农业大学学报, 21(5): 122-125. |
陈辉, 何方. 2000. 锥栗人工林生物量与生产力. 中南林学院学报, 20(2): 11-15. DOI:10.3969/j.issn.1673-923X.2000.02.002 |
胡芳名. 1991. 枣树经济施肥与营养诊断. 林业科学, 27(4): 435-442. |
李贻铨. 1991. 林木施肥与营养诊断. 林业科学, 27(4): 435-442. |
姜远茂. 1995. 红星苹果的营养诊断. 园艺学报, 22(3): 215-220. DOI:10.3321/j.issn:0513-353X.1995.03.014 |
唐守正编著. 1986. 多元统计分析方法. 北京: 中国林业出版社.
|
卫茂荣. 1994. 应用诊断施肥综合法(DRIS)进行日本落叶松苗木营养诊断的研究. 土壤通报, 25(5): 227-229. |
张尧庭. 1980. 多元统计分析引论. 北京: 科学出版社.
|
赵明范. 1991. 核桃叶片N、P、K元素营养诊断指标的研究. 林业科学, 27(6): 652-657. |
Beaufils E R. 1973. Diagnosis and Recommendation Integrated System (DRIS). Univ. Natal Soil. Bull., 1: 32. |
Davee D E. 1986. An evaluation of the DRIS approach for identifying mineral limitations on yield in 'Napoleon' sweet cherry. J. Amer. Soc. Hort. Sci., 111(6): 988-993. |
Fallahi E, Righetti T L. 1984. Use of Diagnosis and Recommendation Integrated System (DRIS) in Apple. Hort. science, 19(3): 116. |
Goh K M. 1992. Preliminary nitrogen, phosphorus, potassium, calcium and magnesium DRIS norms and indices for apple orchards in Canterbury. New Zealand Common. Soil Sci. Plant Anal., 23(13): 1371-1385. |
Parent L E. 1989. Derivation of DRIS norms for a high density apple orchard established in the Quebee Appelachian mountains. J. Amer. Sor. Hort.Sci., 114(6): 915-919. |
Walworth J L. 1986. Preliminary DRIS norms for alfalfa in the southeastern United States and a comparison with midwestern norms. Agron. J., 78: 1046-1052. DOI:10.2134/agronj1986.00021962007800060022x |
 2001, Vol. 37
2001, Vol. 37