文章信息
- 董军, 窦邃.
- Dong Jun, Dou Sui.
- 混沌动力学在森林工程中的应用初探
- STUDIES ON THE APPLICATION OF CHAOTIC DYNAMICS IN FORESTRY ENGINEERING
- 林业科学, 2001, 37(5): 100-106.
- Scientia Silvae Sinicae, 2001, 37(5): 100-106.
-
文章历史
- 收稿日期:1999-07-22
-
作者相关文章
正当人类向21世纪迈进之时, 以非线性理论研究为中心的自然科学领域中正在发生着一次无比深刻的科学革命。70年代出现在非线性科学领域内的混沌学正在科学的舞台上扮演着越来越重要的角色, 正如混沌科学的倡导者之一M.Shlesinger所说:“20世纪科学将永远铭记的只有3件事, 那就是相对论、量子力学与混沌。”混沌是20世纪物理学上第3次最大的革命, 它与相对论及量子力学一样冲破了Newton力学的教规。事实上, 相对论消除了关于绝对空间与时间的幻想, 量子力学消除了关于可控测量过程的Newton的梦, 而混沌则消除了Laplace关于决定论式可预测性的幻想(王东升等, 1995)。以混沌学为主题之一的非线性科学也因此而令人瞩目, 它们横跨于众多的学科间, 探索大自然中复杂的非线性问题, 从不同的角度来揭示复杂自然现象中的规律性。在发展的过程中, 混沌学思想的应用日益广泛, 遍及力学、天文学、物理学、生态学、气象学、生物学、经济学、电子学、信息科学, 甚至音乐、艺术等领域。
混沌学在不同的学科领域中有不同的内涵, 这里所讨论的混沌是以非线性动力学混沌为基础, 具有严格的科学定义, 并进一步以此为前提, 从森林工程科学的角度来进行讨论, 探索其在森林工程科学领域中的应用及其发展前景。
1 混沌动力学研究发展简述混沌学的研究起始于本世纪70年代, 之后它以一种前所未有的广度和深度, 揭开了物理学、数学乃至整个现代科学发展的新篇章, 它将传统的确定论和概率论这两大科学体系相互联系起来, 促进了人类对自然界复杂现象更深层次的认识, 揭示出一个形态和结构崭新的、逼近于真实自然的物质运动世界。最近20年来, 由于现代数学、力学理论和计算机技术的飞速发展, 混沌学正迅速地发展并广泛地向其它的学科渗透, 在科学的发展史上占据了举足轻重的地位。
混沌学虽然起始于70年代, 但其渊源却可以追述到19世纪。19世纪的Newton理论体系为20世纪科学的飞跃———混沌学的创立准备了知识基础。19世纪30年代, 英国的数学物理学家W.R.Hamilton引入了Hamilton函数, 据此人们逐渐认识到在可积和不可积两类动力学系统中, 经典的Newton理论实际上是关于可积系统的理论, 而一般的动力学系统, 则都为不可积的, 这一认识是通向混沌大门的重要一步, 因为混沌正是不可积系统的典型行为。法国数学、物理学家H.Poincare被公认是真正发现混沌的第1位学者, 他以不可积的太阳系中的3体运动为背景, 证明了周期轨道的存在性, 详细研究了周期轨道附近流的结构, 发现了在所谓双曲点附近存在着无限复杂精细的“栅栏结构”。他发现了3体引力相互作用能产生惊人的复杂行为, 确定性动力学方程的某些解有不可预见性, 这就是所谓的混沌动力学现象。但是由于当时的数学水平还不足以解决天体力学中的复杂问题, 因此Poincare曾致力于发展新的数学工具, 他与Lyapunov一起奠定了微分方程定性理论的基础; 为动力系统理论贡献了一系列重要概念, 如动力系统、奇异点、极限环、分岔、稳定性、同宿、异宿等; 提供了许多有效的方法和工具, 如小参数展开法、摄动方法、Poincare截面法等; 他所创立的组合拓扑学是当今研究混沌学不可缺少的工具; 现代动力系统理论的几个重要的组成部分, 如稳定性理论、分岔理论、奇异性理论和吸引子理论等, 都发源于Poincare早期的研究。
在Poincare之后, 一大批数学家和物理学家在各自的研究领域所做的出色工作进一步推动了混沌动力学的发展。G.D.Birkhoff在本世纪20年代期间, 对Hamilton微分方程组正则型求解、不变环面的残存等问题上及不可积系统的轨道特征、遍历理论的研究都有重要贡献。他在研究有耗散的平面环的扭曲映射时, 发现了一种极其复杂的“奇异曲线”, 即为混沌学中的奇怪吸引子。遍历理论在经过了长期的积累之后也取得了重大的进展, 数学家们发现了不同层次的遍历性, 分别代表不同类型的复杂系统; 同时, 弄清了一批具体系统的遍历性和非遍历性, 并且建立了相应区分复杂系统和简单系统的定量判据, 遍历理论最终成为了当今研究复杂系统的强有力的工具。
在20世纪40年代, 人们就从实际中发现, 一类有反馈回路的电子管线路, 可简化为受迫的Van der pol方程
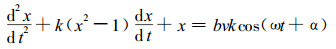
|
(1) |
当k»1时, 系统(1)能产生比外力周期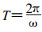
通过十多年的努力, 直到1975年J.E.Littlewood发表了两篇文章, 每篇都长达100多页, 才最终证明了他们所宣布的初步结果。1949年, N.Levinson用分段线性函数代替(1)中的阻尼项, 将(1)改作等价系统
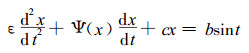
|
(2) |
其中, 0<ε<1, 接着又研究了方程
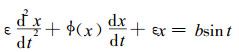
|
(3) |
其中, 
随后在50年代和60年代, Littlewood又发表文章指出, (1)有稳定的11 ω和非稳定的Sω周期解, 不属于(2n+1)ω与(2n-1)ω的类型, 但直到1963年, (1)的解的全部结构如何, 都还不清楚, 其分岔与混沌现象更是一无所知。但不论如何, 上述作者关于方程(1), (2), (3)所提供的张驰振子的研究, 为现代微分动力系统理论的发展提出了刺激性的影响。
1963年, 美国加利弗尼亚大学贝克利分校的动力系统专家S.Smale受到Levinson工作的启发, 为了对Levinson等人的受迫Van der plo方程的几何性质作数学描述, 构造了一个马蹄映射, 给出了具有无穷多个周期点的结构稳定的微分同胚的第1个例子。马蹄映射是有一个具有不变的Cantor集Λ作为极限集合, 并且映射f在Λ上的作用等价于两个符号的Bernoulli移位。这充分说明了系统的随机性质。Smale马蹄映射揭示了事物的本质, 推动了动力系统复杂性研究的发展。
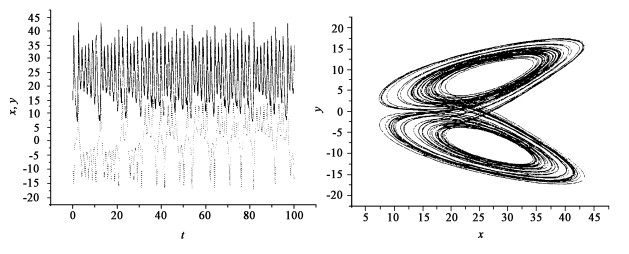
在数学科学领域之外, 就在1963年, 美国麻省理工学院的气象学家Lorenz教授在数值实验中发现, Saltzman在1962年提出的简化的对流模型虽然是一个完全确定的3阶常微分方程组, 但在一定的参数范围内却给出了非周期的看起来是很混乱的结果, Lorenz揭示了一系列混沌运动的基本理论, 如确定性的非周期流、对初值的敏感依赖性、长期行为的不可预测性, 从而发现了今天称之为Lorenz吸引子的典型例子(图 1)。
|
图 1 Lorenz吸引子 Fig. 1 Lorenz attractor |
60年代初, Arnold和Moser独离地研究Kolmogorov在1954年考虑过的接近可积系统的高阶Hamilton系统, 证明了当今称之为KAM定理的著名结果, 被后人称之为发生在以保守系统为研究对象的混沌学研究中第1个重大突破, 是人们用微扰动方法处理不可积系统所取得的一个最成功的结论。KAM定理被国际混沌学界公认为该学科的第1个开端; 我国著名的混沌学者郝柏林院士称KAM定理是“Newton力学发展史上最重大的突破”(郝柏林, 1987; 1983)。混沌学研究的第2大突破是发现了存在于耗散系统中的混沌, 耗散系统在相空间中的体积元是收缩的, 这一突破是以《论确定性的非周期流》(Lorenz, 1963)及其后来的3篇论文为代表(吴详兴等, 1996)。接着Arnold又在1964年进一步发现了Hamilton扰动系统中的随机运动———Arnold扩散。这是确定性保守系统随机性的重要结论, 同时, 法国天文学家Henon等也发现了两自由度不可积Hamilton系统的轨线随能量增大而越来越随机。
“吸引子(attractor)”一词应用于数学中已有40多年的历史。早在1955年, 一些微分方程教材和文献中就引入过此概念, 用于描述非线性微分方程组的稳定平衡点、极限环等。粗略地说, 给定一个微分方程定义的动力系统, 若在相空间中存在一个不变集合, 使其中的某个邻域的所有轨道都逼近于此不变集合, 就称其为吸引子。1971年, Ruelle和Takes的文章首先引入了“奇怪吸引子”的概念(Ruelle et al., 1971), 是为了解释流体力学中湍流发生的机制而引进这个概念的, 在流体中, 湍流是最引人注目的自然现象之一, 如江河湖海中的涡旋, 强大的龙卷风, 跳跃的火焰, 扭曲的彩云, 等都是湍流的例子。“湍流是如何发生?”这个问题是流体力学中百年未解决的难题。Ruelle和Takes所引入的“奇怪吸引子”的概念发展了对湍流的研究, 他们指出, 不是拟周期的周期运动描述了湍流, 湍流发生时, 流体力学体系的行为非常象有限维的通有的可微动力体系, 湍流的产生对应于可微动力系统中出现的某种奇怪吸引子, 即一种对初始条件极敏感的非拟周期的有界运动集合。
1975年Li (李天岩)和Yorke发表了著名的“周期3意味着混沌(chaos)”的文章(Li et al., 1975), 第1次对1维映射给出了“Chaos”的精确的数学的定义。从此, “Chaos”一词被广泛使用于文献中。1976年生态学家May在“自然”杂志上为一个描述种群增长的差分方程的复杂动力系统行为写了1篇综述, 这篇文章起了很大的宣传作用。1978 ~ 1979年, Feigenbaum和Coullet等人独立地发现了3倍周期分岔中的标度性和普适性, 于是研究方向迅速融为一体, 混沌现象引起了广大数学、物理、化学、生物学工作者的关注。
另一方面, 物理、化学实验、流体力学中的湍流实验以及数值计算机模拟进一步揭示了确定性系统存在的类似随机性的混沌现象是无处不在的。混沌并非只是一大堆数学现象, 而是一类新的刚被人们认识的自然现象, 从而使得这类现象的研究很快成了数学物理研究中的热门。
在混沌的研究中, 横截同宿现象是一个很重要的概念, 本世纪20年代Birkhoff曾潜心研究这个问题, 他证明了2维系统中的横截同宿点的每个邻域有无穷多周期轨道, 因此显示了一类新的复杂性。60年代, Smale等人对上述问题进行了更广泛的研究, 并证明了Smale-Birkhoff定理:对某个适当大的整数N, 横截同宿点的存在, 意味着在离散轨道的某些迭代式中存在Smale马蹄, 而马蹄是结构稳定的。一些专家认为, Smale的发现, 对于今天人们理解动力系统复杂的非周期的混沌性质, 起着划时代的作用。
70年代, B.Mandelbrot创立了分形学并用分形的观点来描述相空间中的复杂图形, 为混沌学的研究提供了新的几何工具。随之而来的是吸引了许多理论及实验工作者纷纷加入了混沌学的研究, 从此混沌学的研究逐渐进入了一个活跃的时代。
在我国的物理学界, 以郝柏林院士为代表的一批科学工作者对分岔和混沌的数值研究作出了很大的成绩; 在数学界, 许多动力系统分支与混沌理论研究的专家在理论上作出了重要贡献。1984年朱照宣教授在《力学进展》(朱照宣, 1984)上和郝柏林院士在《物理学进展》(郝柏林, 1983)上发表的两篇综述报告, 1983年在桂林召开的全国数学家、物理学家、力学家等共同参加的混沌学术会议, 1986年由昆明理工大学承办了的全国分岔与混沌讲习班, 目前国内的一批分岔与混沌研究的学科带头人都参加过这个讲习班的活动。这以后, 类似的学术会议不断地举办召开, 有关分岔与混沌方面的学术论文不断地涌现, 并且有一定数量的专著出版, 包含分岔与混沌研究的非线性科学还被列入了国家重大攻关项目和攀登计划。黄克累①在文中论述了混沌研究的历史和现状, 并展望了发展前景; 陈予恕在文(陈予恕, 1992)中系统地总结了我国学者在分岔与混沌研究方面取得的众多成果; 徐建学在文(徐建学, 1992)中总结了非线性动力系统大范围分析方面取得的进展。此外, 在应用方面, 随着理论研究的不断深入, 其应用领域也在不断拓广, 如在通讯中的应用(吴详兴等, 1996)、在化学反应动力学中的应用(李后强等, 1993; 唐云, 1992)、在生物系统中的应用(井竹君等, 1992; 陈兰孙等, 1993)、在经济学中的应用(吴详兴等, 1996; 黄登仕, 1992)等。
① 黄克累.混沌研究的历史、现状和展望.成都:全国第六届非线性振动学术会议综述报告, 1992。
2 森林工程科学中的非线性问题与混沌动力学复杂性是非线性科学理论共同研究的最基本的内容, 森林工程根据它所研究的对象, 存在着许多的复杂现象, 吸引着人们去探索。森林工程科学是一个很综合的学科, 通常包括森林的生态森林采伐、木材运输、木材贮存等几个阶段, 它们之间相互联系, 构成一个很综合的非线性系统, 具体又涉及规划、工程工艺、生产技术、机械以及生态环境等。
森林工程中的动力系统模型是十分丰富的, 从大的系统到小的系统, 在环境的控制参数的控制下, 表现出十分丰富的变化过程。例如, 任何一个生物群体, 都必须不断地进行“吐故纳新”, 这个群体才会兴旺发达, 森林也是如此。多年的实践证明了的抚育性采伐将促进森林的生长, 问题的关键在于如何进行抚育性采伐, 才能不破坏伐区的生态, 从而保持各种生物群体的相对稳定, 而且还有助于林木的生长, 进而实现森林资源的永续利用和可持续性发展。如何进行抚育性采伐?按照我们今天人类对大自然的认识, 绝不再是多采几根或少采几根木头的问题, 而是牵扯到采伐工艺过程、作业技术、采伐强度和动力噪音、环境污染以及生物种群和种群之间的相互作用、种群和环境之间的相互作用等等, 这些繁杂的错综的关系就是非线性问题在自然界中的具体表现, 这些关系在随时间的变化而变化, 所构成的系统就称为非线性森林工程动力系统, 或称为非线性森林工程演化系统, 混沌动力学则是研究非线性森林工程动力系统的一类理论工具, 动力系统的主要目标是研究随时间的长期发展下, 系统的状态是如何改变和演化的。
又如, 木材贮存中的腐朽降等, 通常采用物理或化学方法进行防腐, 具体到一个区域、一个场地、一个楞头, 对一定的树种, 具备多大的温度、水份和空气含氧量最适合木腐菌的生存与繁殖?如果把温度、水份和含氧量作为所考虑系统的控制参数, 在找到适合描述上述问题的数学模型方程, 则这就是一个完整的非线性森林工程动力系统模型, 一般说来, 这样的模型往往是由偏微分方程组或常微分方程组构成, 需要采用现代动力系统的研究方法, 如混沌动力学方法, 对它进行理论上的定性分析和定量数值计算, 便可得到模型随控制参数演化的过程, 同时得到最佳的控制参数, 反过来还能够科学地指导生产。伐木工人的职业病之一“白手病”, 是由于常年在低温条件下受汽油的熏染和机械的振动而形成的, 这实际上也是一个参数控制下的非线性森林工程动力系统问题。
在上面所提到的各个方面, 都存在着复杂的非线性行为, 无疑要探索清楚这些问题, 将会促进整个森林工程学的发展, 同时使人们能够在现代科学的基础上认识森林工程这个学科。然而要真正地搞清这些复杂的非线性问题, 仅靠单一的学科是无能为力的, 即使不同的学科专家坐在一起, 也是各说各的理, 原因是问题和问题之间(即系统和系统之间)的相互作用是非线性的, 整体并不等于部分之和。要对上述问题给予解答, 必须建立描述系统整体行为的理论体系, 而这样的体系绝不是各分支学科的简单组合和对接, 而必须用非线性理论来建立它们之间的联系, 从而揭示出森林工程学中研究对象的内在规律。
如果我们假设某个问题变量(例如X)是时间t、具体点的空间坐标x及某些相互联系的控制参数k的函数, 则根据一定的守恒规则或基本原理, 就可得到描述问题背景的模型方程
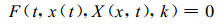
|
(4) |
其中, x表示具体的空间坐标, 可以是1维的、2维的、3维的, X所考虑问题的变量, 可以是单个变量, 也可以是多个变量; 控制参数k可以是单个参数, 也可以是多个参数; 这里F可能是一个由变量组成的相互耦合的偏微分方程组(PDEs), 也可能是一个常微分方程组(ODEs)。根据微分方程理论可知, 当上述微分方程组在一定的初边值条件下, 便可构成一个完整的定解问题(数学模型), 它表达了该系统在一定的参数控制下, 随时间的变化过程, 这就是一个动力系统模型, 有的文献中也称之为演化系统模型。当然模型可能会存在各种各样的解, 例如周期解、非周期解。我们主要关心(4)式在参数变化下, 其解的性质的变化。非线性科学理论解决这类问题提供了新的思维方式和解决问题的方法; 分形理论则为揭示复杂现象提供了一种新型的几何工具。
下面的一个简单模型可以清楚地说明上述思想。可持续性发展的研究是人类对自然资源利用的一个新的辩证观点, 在森林工程科学中是一个重要的研究分支。我们考虑如下某个林区一个理想的可持续性发展动力学模型
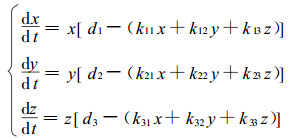
|
(5) |
其中, 以x, y, z分别表示某伐区内的林木密度、森林的采伐强度、森林中生存动物的分布密度, 可以看出在这个系统中, 变量之间是相互制约、相互影响的, 以kij表示j类密度对i类密度的约束参数因子, di为适当的参数, 这是一个类似于Lotka -Volterra模型的问题, Vance曾揭示了其解的分岔与混沌的特性(陈兰孙等, 1993), 本文取参数为
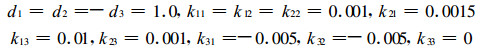
|
时, 经过数值计算, 得到了如图 2和图 3所示的混沌现象, 和Vance等人的理论分析结果是一致的, 模型说明当参数维持在一定的范围内时, 系统将是可持续发展的; 若参数变化超过一定的范围, 例如人类的采伐行为过大时, 系统将出现多个周期的恶性循环, 即混沌现象。
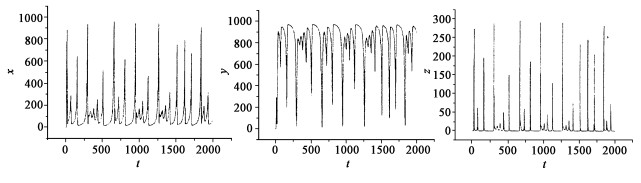
|
图 2 解x(t), y(t), z(t)的波形图 Fig. 2 Solution of x(t), y(t), z(t) |

|
图 3 模型混沌解图 Fig. 3 The chaotic solution of the model (5) |
通过上面的例子说明了非线性森林工程动力系统研究的意义和重要性, 同时也揭示了分形与混沌在森林工程科学中的应用前景。森林工程学科的界定, 国际虽未形成统一的说法。但我国该领域的学者对森林工程(也称森林作业科学与技术或林业工学)学科内涵的描述是恰如其分的。那就是, 森林工程是森林资源建设与保护、开发与利用中的非生物工程。其研究对象是作业者、作业设备、森林环境、作业环境、交通通讯及其网络等等; 其研究目标为寻求一种或几种适宜的作业方案(包括工程), 使得森林作业活动在森林可持续发展和环境生态效益指标约束下, 获得最优或次优的社会经济效益。森林工程大的前导工序是森林采伐, 它是人类直接作用和影响森林生物群体的一道工序。直观地说, 就是通过采伐, 把有生命的森林中的一部分树木使其死亡来服务于人类; 由于部分生命的死亡, 反而使活着的生命更好, 更健壮, 这就是森林资源的永续利用和可持续发展。
生命现象远比物理、力学现象要复杂得多, 它是包含有物理、力学现象且还含有更复杂事物的一类现象。因此生命科学如果只停留在定性的研究水平上是不够的, 从定性研究发展到定量的研究, 是科学发展的必然规律。一门科学只有当它充分利用数学工具时才算发展到了比较完善的阶段。一棵不采, 不是科学; 无限量地采伐下去, 更不是科学。森林工程学的目的是如何利用科学采伐使森林越采越多、越采越好, 这就要用非线性森林工程动力系统的理论及有关数学工具来探讨生命科学中的混沌动力学现象。
诚然, 混沌动力学是探索复杂性的一种有效的方法, 但问题的关键还在于如何建立准确反映实际问题背景的数学非线性森林工程动力系统模型, 这需要用到多学科知识的交叉, 这里面存在着相当多的问题有待于人们进一步去探索。有了完整的数学模型后, 就可以利用解决动力系统的一系列现代数学方法、计算机仿真方法等工具来分析系统, 找到其出现定性性质突变或分岔的参数点, 通向混沌的关键参数值, 深刻分析这些参数的实际背景及意义, 从而对实际的生产作业等的给予理论上的指导。我们相信, 经过科学工作者的不断探索和努力, 数年前周恩来总理所提出的“越采越多, 越采越好, 青山常在, 永续利用”的遗愿一定会得到实现。
陈兰孙, 陈键. 1993. 非线性生物动力系统. 北京: 科学出版社, 53-110.
|
陈予恕. 1992. 非线性振动.分岔和混沌理论及应用. 振动工程学报, (3). |
井竹君, 林怡平. 1992. 分岔理论在高维生物模型中的应用. 数学的实践与认识, (4). |
郝柏林. 1987. 牛顿力学三百年. 科学, 39(3). |
郝柏林. 1983. 分岔, 混沌, 奇怪吸引子, 湍流及其它——关于确定系统中的内在随机性. 物理学进展, (3): 392-396. |
黄登仕. 1992. 非线性经济学中的混沌和分形. 大自然探索, 10(37). |
李后强, 汪富泉. 1993. 分形理论及其在分子科学中的应用. 北京: 科学出版社, 58-80.
|
唐云. 1992. 分岔理论方法在化学反应器研究中的应用. 数学的实践与认识, (3). |
王东升, 曹磊. 1995. 混沌、分形及其应用. 中国科技大学出版社, 1-24.
|
吴详兴, 陈忠. 1996. 混沌学导论. 上海科学技术文献出版社, 1-56.
|
徐建学.非线性动力系统大范围分析, 见: 舒仲周主编.稳定、振动、分岔与混沌研究, 中国科学技术出版社, 1992, 6~15
|
朱照宣. 1984. 非线性力学中的混沌. 力学进展, (2). |
Li T Y, Yorke J A. 1975. Period three implies chaos. Am.Math.M onthly, (82): 985-992. |
Ruelle D and Takens F.On the nature of turbulence.Common.Math.Phys.1971, (20): 167~192, (23): 343~344
|
 2001, Vol. 37
2001, Vol. 37
