林业科学  2001, Vol. 37 Issue (2): 117-121   PDF    
0

文章信息

郭明辉.
Guo Minghui.
人工林红松木材生长轮密度动态模型建立与预测
THE ESTABLISHMENT AND PREDICTION OF THE DYNAMIC VARIATION MODEL OF WOOD GROWTH RING DENSITY FOR THE PLANTATION FOREST OF PINUS KORAIENSIS
林业科学, 2001, 37(2): 117-121.
Scientia Silvae Sinicae, 2001, 37(2): 117-121.

文章历史

收稿日期：1999-11-18

作者相关文章

郭明辉

引用本文
郭明辉. 2001. 人工林红松木材生长轮密度动态模型建立与预测. 林业科学, 37(2): 117-121.
Guo Minghui. 2001. THE ESTABLISHMENT AND PREDICTION OF THE DYNAMIC VARIATION MODEL OF WOOD GROWTH RING DENSITY FOR THE PLANTATION FOREST OF PINUS KORAIENSIS. Scientia Silvae Sinicae, 37(2): 117-121.  
人工林红松木材生长轮密度动态模型建立与预测
郭明辉     
东北林业大学 哈尔滨 150040
收稿日期：1999-11-18
基金项目：黑龙江省攻关资助项目(G99B5-3)
摘要： 本文根据人工林红松木材生长轮密度变异特点, 采用时间序列分析法, 建立了人工林红松木材生长轮密度的动态模型, 对木材生长轮密度进行近期预测, 预测结果良好。此研究结果实现了木材生长轮内的材质预测, 为人工林红松的定向培育提供理论依据。
关键词： 人工林    红松    木材生长轮密度    动态模型    材质预测    
THE ESTABLISHMENT AND PREDICTION OF THE DYNAMIC VARIATION MODEL OF WOOD GROWTH RING DENSITY FOR THE PLANTATION FOREST OF PINUS KORAIENSIS
Guo Minghui     
Northeast Forestry University Harbin 150040
Abstract: This paper according to the variational characteristics of wood growth ring density, by the method of time sequence statistics, the seasonal variation model of wood growth ring density was established.We can achieve short-term forecast of wood growth ring density and early-stage forecast of the quality of wood growth ring density. The results provided a scientific basis for processing of plantation forest.
Key words: The plantation forest    Pinus koraiensis    Wood growth ring density    The dynami variation model    Quality prediction    

木材的生长轮密度是木材重要的物理指标之一。在树木生长形成木质部的过程中, 由于外部环境生态因子、立地条件、培育措施以及树木本身遗传因子的影响, 使木材的材质具有广泛的变异性(Zobel et al., 1978;1989)。木材生长轮密度是表征木材材质综合性变异的重要指标。通过分析生长轮内木材密度的变异, 可以探明树木形成过程中, 各种外在因素和内部遗传特性的表征。在研究木材生长轮材质变异规律的过程中发现, 木材材质变异规律极其复杂(李坚等, 1993); 材质变异在某些解剖特征方面具有一定的规律性, 但在某些特征如生长轮密度、生长轮宽度等方面具有很大的波动性(Michael, 1989; Panshin, 1980), 给木材生长轮材质变异规律的数学方法拟合带来了一定的困难。

已往对木材生长轮材质变异规律的研究多采用统计回归的方法建立生长轮材质变异规律的数学模型, 多取得了较好的效果; 但对某些变异性较为复杂的材性指标, 其拟合精度和相关性相对较低, 有时甚至难以表达和描述出木材自身的变化特点, 有鉴于此, 有必要根据木材生长轮材质变异特点。寻求一种更为准确和理想的数学方法, 用以拟合木材生长轮材质的复杂变异规律。

1 木材生长轮密度时间序列模型研究的可行性

时间序列是按照时间顺序取得的一系列观测值, 数据是以时间序列的形式表现, 其典型的本质特征就是相邻观测值的依赖性。木材生长轮密度是按时间顺序的一系列测试值, 相邻数据点间有着必然的联系。树木在形成木质化的过程中, 记录着树木生长环境和立地条件以及遗传性的一切特征, 这为采用时间序列理论建立研究木材生长轮密度的数学模型奠定基础。

大量的实验研究表明, 采用时间序列分析方法, 应用自回归滑动模型(ARMA)和非稳态自回归滑动平均模型(ARIMA)(王金满, 1997)以及季节模型ARIMA(p.d.q)(P, D, QS), (p、q为自回归、滑动平均的阶次, d为差分运算阶次)基本上拟合了木材生长轮密度实测数据的变化规律。

2 木材生长轮密度变异规律模型

本实验采用32年生红松人工林为试材, 对人工红松林木材生长轮密度进行时间序列模型建立与预测, 采用X射线微密度扫描仪测量木材生长轮密度, 得到自髓心向树皮方向连续的木材生长轮密度变化曲线, 并用时间序列分析方法, 建立生长轮密度变异规律模型。

根据试验采集的数据, 用STATISTICA 5.0版统计分析软件进行时间序列分析, 观察原生长轮密度的自相关系数和偏相关系数曲线, 选择参数p, d, q, 和P, D, QS。对数据进行分析, 得到参数模型(表 1)。

表 1 木材生长轮密度ARIMA(1, 1, 1)(0, 0, 1)12模型参数 Tab.1 The parameter of the model ARIMA(1, 1, 1)(0, 0, 1)12 of wood growth ring density

由表 1的模型参数统计及检验结果可以看出, 选择上述模型对木材生长轮密度进行建模, 可以标出生长轮内木材密度的变化情况, 为人工林木材材质的预测和经营措施的改进提供相应的理论基础。各参数项的相关性如表 2所示。

表 2 模型ARIMA(1, 1, 1)(0, 0, 1)12参数相关性 Tab.2 The parameter correlation of the model ARIMA(1, 1, 1)(0, 0, 1)12

从表 2的参数项的相关系数可以看出, P(1), Q(1)的相关性较大, 而QS(1)与P(1)和Q(1)的相关性较小。这说明在木材生长轮的时间序列内存在着明显的季节性, 与树木在形成木质层部的过程中, 具有季节生长特性有直接关系。

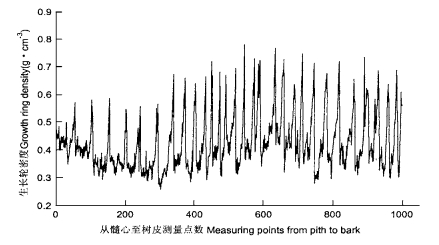
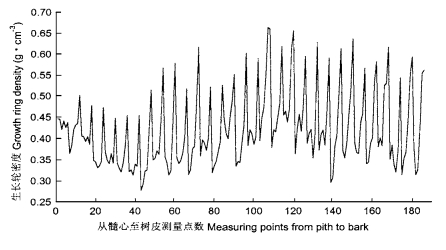
3 木材生长轮密度时间序列预测模型

根据对生长轮密度变异规律时间序列模型的分析可知, 采用季节性回归分析, 可以拟合木材生长轮内的细节变化趋势。但是为了统一每一生长季的年轮内木材密度时间序列测试数据, 必须对连续测试数据归一化。根据红松的生长习性, 每年确定为6个月的生长周期(丁宝永, 1981; 蒋伊尹, 1994), 对每一生长轮内的数据平均分成6等份; 求其密度平均值, 进行重新归一化的数据的建模, 使生长轮密度的预测具有规范性质。对实验数据进行归一化处理, 未处理前的生长轮密度曲线如图 1所示, 进行归一化以后的密度变化曲线如图 2所示。从图 1和图 2的比较可以看出, 后者在和节性趋势的表达性方面更为直观。

图 1 人工林红松木材生长轮密度变化曲线 Fig. 1 The variational regulation of wood growthring density of Plantation forest of Pinus koraisensis
图 2 归一化木材生长轮密度变化曲线 Fig. 2 The normalized variation regulation of wood growthing density

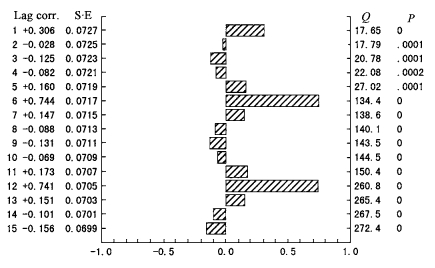
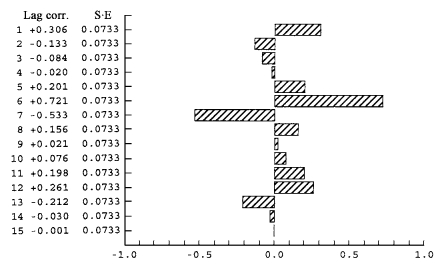
时间序列模型预测是时间序列的当前和过去值对未来值的预报。首先确定惯性系统的传递函数, 即确定输入和输出模型, 由此可以描述任一给定输入序列对模型输出的影响。对图 2所示的时间序列进行建模, 首先观察原始时间序列的自相关和偏相关系数, 即图 2的自相关和偏相关变化曲线如图 3和图 4所示。

图 3 自相关函数 Fig. 3 Autocorrelation function Lag Corr.为滞后系数 Lag corr .is the lag coefficient;S.E.为标准误差 S.E is the standard error
图 4 偏相关函数 Fig. 4 Partial correlation function

由图 3和图 4可以看出, 该序列为非稳态序列, 具有明显的季节性和周期性, 季节性为12, 周期性为6左右。通过反复模拟试验, 确定模型为ARIMA(1, 1, 0)(1, 1, 1)12, 其具体参数如表 3所示。

表 3 模型(1, 1, 0)(1, 1, 1)12参数 Tab.3 The parameter of the model ARIMA(1, 1, 0)(1, 1, 1)12

由表 3知, 确定的模型中的参数具有较显著的相关性。通过对自相关和偏相关系数检验, 验证模型具有可靠性。建模后残差的自相关和偏相关函数如图 5和图 6所示。

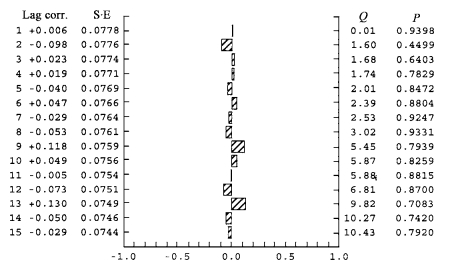
图 5 残差自相关函数图 Fig. 5 Residual autocorrelation function
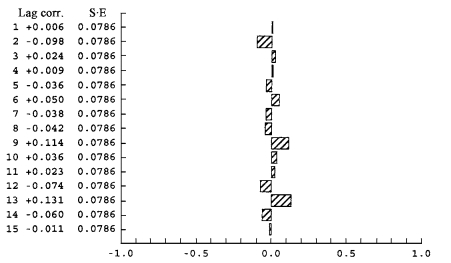
图 6 残差偏相关函数图 Fig. 6 Residual partial correlation function

由图 5和图 6可知, 模型残差完全在可信区间内, 可以使用该模型进行预测。对实验数据生长轮密度进行预测, 预测结果如图 7所示。

图 7 人工林红松木材生长轮密度预测曲线 Fig. 7 The forecast regulation of wood growthring —Observed ---Forecast 0.0000%

由图 7预测曲线可以看出, 在生长轮最后2 a内, 具有很好的拟合预测结果, 实现了生长轮内材质预测。其预测结果的比较见表 4。

表 4 模型预测数据对比 Tab.4 The contrast of measured data and forecast data
4 生长轮密度时间序列预测评价

采用时间序列季节模型对木材生长轮密度进行近期预测, 可以实现生长轮内材质预测。同以往木材生长轮材质预测方法比较, 该方法具有更准确的预测分析精度, 可为人工林培育措施的制定提供理论依据。

参考文献(References)
丁宝永等.红松人工林季节周期生长规律的研究, 东北林学院学报, 1981, (4): 19~32 http://www.cnki.com.cn/Article/CJFDTotal-DBLY198104002.htm
蒋伊尹. 1984. 红松人工林生长与生长模型. 东北林学院学报, (2): 6-15.
李坚等编著.生物木材学.哈尔滨: 东北林业大学出版社, 1993
刘一星. 1990. 软X-射线法测定木材生长轮密度的研究. 林业科学, 26(6): 33-39.
王金满. 1997. 木材材质预测学. 哈尔滨: 东北林业大学出版社.
Panshin A J, Carl de Zeeuw. 1980. Textbook of wood technology. Mcgraw-Hill book company.
Michael C. 1989. Extreme radial changes in wood specific gravity in some tropical pioneers. Wood and fiber science, 20(3): 344-349.
Zobel B J, Van Buijtenen J P. 1989. Wood variation its causes and control. Spring-Verlag.
Zobel, et al. 1978. Improving wood density of short rotation Southern pine. Tappi, 61(3): 41-44.