文章信息
- 侯祝强, 蒋礼, 胡继青.
- Hou Zhuqiang, Jiang Li, Hu Jiqing.
- 木材干燥预热过程的水分流和热流分析
- THEORETICAL ANALYSIS ON THE MOISTURE FLUX AND HEAT FLUX IN PROCESSES OF WOOD PRE-HEATING
- 林业科学, 2000, 36(2): 103-109.
- Scientia Silvae Sinicae, 2000, 36(2): 103-109.
-
文章历史
- 收稿日期:1999-08-01
-
作者相关文章
2. 中南工业大学热学物理系 长沙 410083;
3. Forestry College, Oregon State University, C orvallis, OR 97330, USA
2. Department of Physics and Heating, Central South University of Technology Changsha 430083;
3. Forestry College, Oregon State University, Corvallis, OR 97330 USA
在木材干燥特别是高温干燥前进行预热, 不但可以避免或减少干燥过程中产生的干燥缺陷(如干燥开裂、干燥曲翘等) (Simpson, 1976; Alexiou, 1990), 而且还可以加快干燥速度降低干燥成本。非平衡态热力学线性理论已应用于木材非等温扩散以及木材干燥的有关问题中(Siau, 1983; Siau et al., 1985; Skaar, 1985;Nelson, 1989), 但迄今不见有关于求解线性流耦合方程开展研究工作的报道。本文将通过求解非平衡态热力学线性流耦合流方程, 对于木材干燥预热过程中的水分流和热流进行分析和计算。
1 水分流和热流耦合方程理论和实践都表明, 介质中存在着几种不同的不可逆热力学过程时, 其相互间将会产生耦合作用, 而这些过程距离平衡态不远时, 可以使用线性唯象方程进行描述(林瑞泰, 1995)。因此, 当含有水分的多孔介质被加热时, 介质内部会同时存在着水分流和热流, 而同时存在着的水分流和热流两者间要相互影响产生耦合作用。这时多孔介质内的水分流即质量的输运, 并不是单一的因含水率梯度导致的输运, 相应的热流即能量的输运也不是单一的因温度梯度导致的传热, 必须考虑水分流和热流间的耦合作用, 从而才能全面地反映此时水分流和热流的特性。
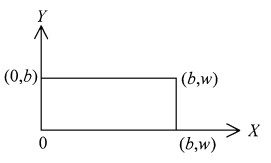
设被加热的含水多孔介质横截面为矩形, 截面几何尺寸与其长度相比很小。这样, 沿长度方向的水分流和热流可忽略, 只须考虑介质横截面上水分和热的二维输运流。建立如图 1所示的平面直角坐标系, x、y分别沿介质横截面相互垂直的两个边, W、b是介质横截面的宽度和高度。忽略介质内部其它物质和空气的扩散, 则只存在水分流
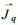

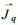
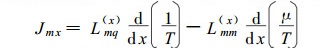
|
(1) |
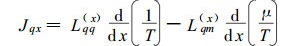
|
(2) |
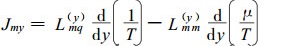
|
(3) |
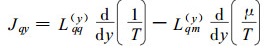
|
(4) |
|
图 1 介质横截面坐标下载原图 Fig. 1 The coordinate scheme of sample cross-section |
(1) 式与(3)式以及(2)式与(4)式在数学表达上是类同的, 我们只须就(1)式和(2)式讨论多孔介质中水分流和热流方程的形式, 所得结果可用于(3)式和(4)式。根据输运热Q*和输运能U*的定义有(DeGroot, 1981; Halsopoulos et al., 1986),
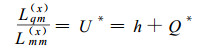
|
(5) |
(5) 式中h为摩尔焓。
借用DeGroot (1981)关于耦合流方程的变换方法, 导出(1)式和(2)式中的Onsager系数的具体形式。当多孔介质内无温度梯度时, 由(1)式和写成以化学势梯度为驱动力的形式Fick第1扩散定律, 得
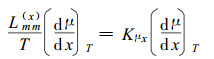
|
式中:Kμx是以水的化学势梯度为驱动力时多孔介质在x方向的扩散水分系数。从而有
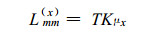
|
(6) |
当不考虑多孔介质内水分输运对传热的影响时此时介质传热服从定律且式中水分扩散流对应的项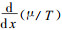

|
即
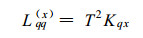
|
(7) |
式中:Kqx为不存在水分输运时多孔介质在x方向的导热系数。如若不考虑电磁加热则无电磁场存在, 唯象系数的Onsager倒易关系成立(德格鲁脱等, 1981), 将(6)式和(7)式分别代入(1)、(2)两式中, 利用热力学关系式μ=h-TS和Onsager唯象系数倒易关系经整理后得到,
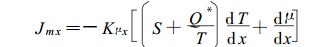
|
(8) |

|
(9) |
式中:S为木材中水分的摩尔熵。(8)、(9)式即为本文关于在长直的矩形截面多孔介质中, x方向水分流和热流的耦合方程, y方向的水分流和热流耦合方程具有与上两式类似的形式写出如下:
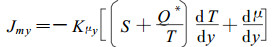
|
(10) |

|
(11) |
(10) 式和(11)式中有关量的意义与(8)式和(9)式相应量相同。以下我们将把上述方程应用于典型的多孔介质—木材中, 分析和计算木材干燥预热过程中的水分流和热流。
2 干燥预热过程中的水分流特性 2.1 干燥预热过程中的水分流方程在干燥前用水蒸气或饱湿的空气加热含水的木材, 以避免木材在干燥中开裂和曲翘, 这即为木材的干燥预热。木材可视为正交各向异性体, 分别将x方向和y方向取为木材细胞排列的径向和弦向, 从而可以将(1)式和(2)式应用于木材径向水分流和热流, 而(3)式和(4)式则可应用于弦向的水分流和热流。干燥时木材内的含水率和温度分布具有空间对称性(Gu Lian bai et al., 1984; Rice et al., 1991), x方向和y方向的流方程除与木材结构有关的参数有差异外, 两者再无其它差异。以下只讨论x方向的流方程, 所得结果对y方向流方程同样有效, 只须将x方向的有关量换成相应y方向的量。
预热介质是饱湿的, 木材样品表面无水分蒸发。预热前木材的含水率均匀分布, 因而木材内不出现因含水率梯度存在产生的水分流。因无水分蒸发且预热木材含水率大, 不存在束缚水的输运流, 并且水蒸汽输运流相对于液态水输运流来说可忽略。这样就有μ=μW、h=hW、S=SW, Q*=QW*且有(Nelson, 1986)
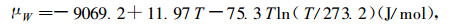
|
(12) |
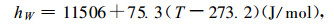
|
(13) |
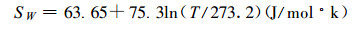
|
(14) |
从而

|
(15) |
将上式代入(8)式经整理后有

|
(16) |

|
(17) |
设垂直于x方向的木材样品表面积为Sx, 在t0时间内由该表面进入木材的水分质量,
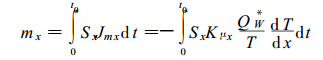
|
(18) |
忽略木材结构非均匀性对温度分布的影响, 从而任一截面上中心点的温度都相同。长直均匀的固体材料在加热过程中其内部温度变化的表达式为(Kollman et al., 1968) :
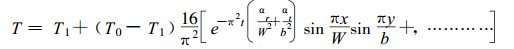
|
(19) |
式中:T0为加热开始时木材初始温度, T1为木材表面温度(即加热介质温度), W、b分别为木材在x方向y方向上的长度, ar、at在这里分别为木材的径向和弦向导热系数, 坐标选择如图 1所示。(19)式是一个收敛相当快的级数, 在很多情况下只需计算第一项(Kollman et al., 1968)。
根据导温系数的定义,
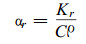
|
(20) |
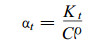
|
(21) |
式中:Kr与Kt分别为木材样品的径向与弦向导热系数, C为木材的比热, ρ为木材的密度。通常Kr和Kt不相等, 取Kr/Kt=1.10计算(Kollman et al., 1968)。若木材样品密度ρ=0.4, 含水率为100%时, 有(ar+at) /2=0.0004 (m2/h) (Kollman et al., 1968)。这样由(21)、(22)两式可得, ar=0.00043 (m2/h), at=0.00039 (m2/h)。
根据前述的理由, 取(19)式第一项对其求x的导数后得,
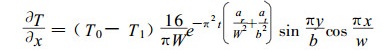
|
水分流由木材的表面进入木材内, 取d T/dx为木材表面处的温度梯度计算水分流, 则在木材与y方向垂直的两个表面有,
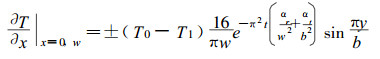
|
(22) |
x=0和x=w的两个表面上温度梯度大小相等方向相反, 所以上式中出现“±”。这里仅计算x方向输入的水分的数量不考虑其空间分布, 使用木材表面温度梯度对y的空间平均值计算水分流, 这样
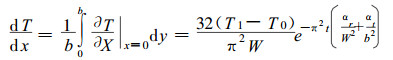
|
(23) |
根据(20)式的计算并结合实验观察, 木材表面温度在加热5 min后即与加热介质温度相同, 所以在积分计算由x方向进入木材的水分mx时, 有关量中的温度参数均可取加热介质温度。将(23)式代入(18)式积分后得到由x方向上2个表面进入木材的水分,
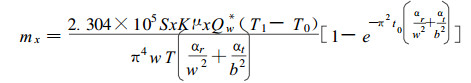
|
(24) |
(24) 式中Sx=bL且L为木材样品的长度。
根据(17)式并重复上述讨论, 可以得到由y方向上两个表面进入木材内的水分,
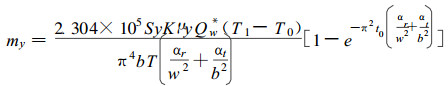
|
(25) |
式中:Sy=wL, 为垂直于x方向木材样品一个表面面积。如前所述, 忽略样品两端的纵向流, 则进入样品的水分总质量,
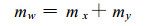
|
(26) |
利用Nelson的推导方法(Nelson, 1991), 可以得到
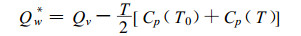
|
(27) |
式中:T0=273.2 K, Qv为液态水的蒸发热, Cp为液态水的定压比热(Nelson, 1986),
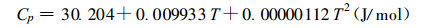
|
(28) |
含水率在40%以上时木材横向导热系数为(Siau, 1984),
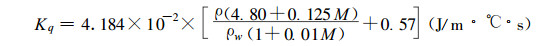
|
(29) |
式中:ρ为木材的密度, ρw为液态水的密度, M为木材的相对含水率。
根据化学势为驱动力的水分扩散系数与水分蒸汽压为驱动力的水分扩散系数的关系, 可以得到,

|
(30) |
式中:H为相对湿度, R为气体普适常数, P0为饱和蒸汽压且有(Skaar, 1988),
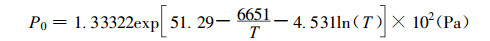
|
(31) |
此外:Kp的表达式为(Bramhall, 1979),
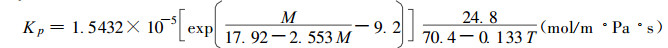
|
(32) |
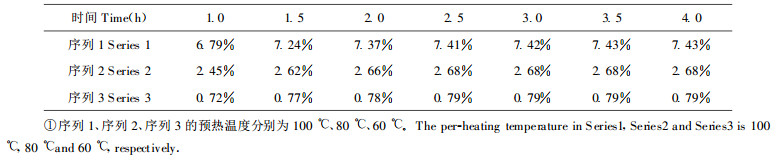
若预热木材长为L=2.00 (m), 不计木材扩散系数在径向(x)与弦向(y)的微小差异; 设预热前木材的温度为20℃, 根据(24)、(25)、(26)式利用前述有关参数的计算式, 按60℃、80℃、100℃3个不同的预热温度, 算得的不同预热时间内木材含水率增量如表 1所示。对于预热时间为4.0h的3个不同温度预热过程, 木材含水率增量在0.79%~7.43%的范围内, 这一结果为Simpson关于木材预热4h后(Simpson, 1976), 含水率的变化在几个百分点内变化的实验结论相一致。同时可知, 预热温度越高, 木材含水率的变化越大。
|
|
根据输运热的定义, 此时与水分热扩散对应的输运热应取负值, 在木材预热的温度范围内hW > 0, 由(9)式、(11)式和(15)式及输运能和输运的关系, 可以得到木材干燥预热的热流方程,
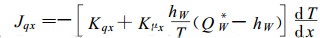
|
(29) |

|
(30) |
重复2.2节关于水分流的讨论过程, 根据(29)式和(30)式分别可以得到沿x方向和y方向进入木材的热量, 以及进入木材的总的热量,
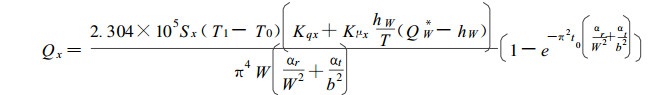
|
(31) |

|
(32) |
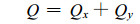
|
(133) |
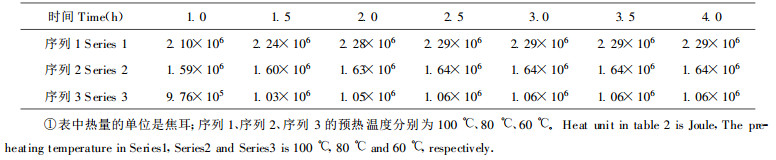
表 2中3个序列的预热起始温度均为20℃, 根据表中的数据可知, 虽然预热温度不同但在预热3 h之后, 3个序列进入木材的热流都不再变化, 而热流不变化即木材内部的热传输已达到稳定状态。Gu Lianbai (1984)曾在56.1℃和100℃对木材干燥预热进行对比实验, 结果表明木材样品在这两种情况下预热3h之后, 其内部温度都达到了与预热温度相同的值。他的实验结果与本文关于木材达到热稳定状态与预热温度大小无关的结论是一致的。
|
|
(29) 式和(30)式圆括号中两项符号相反, 表明水分流对热流的耦合作用存在效果相反的两个因素, 由计算知QW* > hW, 故总的效果仍是使热流增大。预热过程中进入木材样品中的热流分为两部分, 一部分是通过热传导的方式由外向内输送, 另一部分是通过木材中水分对热流的耦合作用的方式由内向外输送。设前者为
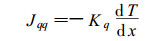
|
(33) |
后者为
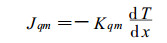
|
(34) |
并且

|
(35) |
由热传导输送的热量和木材中水分耦合作用输送的热量比率分别为,

|
(36) |
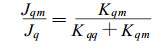
|
(37) |
根据Kqq和Kqm在x和y方向的平均值, 对于3个不同的预热温度并且当木材含水率为100%时, 由(42)式算得因水分耦合作用所输送的热量比率分别为11.9%、6.6%和3.3%。
4 讨论与结论本文运用在预热介质边界表面积分的方法求解了线性耦合流方程, 获得了水分流和热流在预热介质表面的解; 同时, 利用所得的解具体计算了木材干燥预热过程中的水分流和热流, 讨论分析了两个流之间的耦合, 计算所得的结果与以往的有关实验结果吻合。
在木材预热干燥过程中的水分流是由于温度梯度而导致的热扩散流, 无法利用通常的扩散方程进行讨论, 而本文通过解耦合流方程所得结果能得到实验的证实, 这表明耦合流方程是分析多孔物质干燥过程的一个有效方法, 它既可以从机理上揭示流相互之间的耦合特性, 又能够对于水分流和热流进行定量描述。
预热中木材内部的温度低于加热介质, 因Soret效应将出现输入木材内的水分热扩散流, 预热结束时木材含水率将有增加。由计算知, 在预热前两小时内木材的温度和含水率就已接近预热结束时的值, 输入木材的水分和热量主要发生在这一阶段。这样, 可以根据木材干燥的温度来选择适当的预热温度在预热的前两小时内完成预热要求从而节约时间提高效率.
德格鲁脱SR, 梅修尔P著, 陆全康译.非平衡态热力学.上海: 上海科学技术出版社, 1981, 28~33
|
李如生. 1986. 非平衡态热力学和耗散结构. 北京: 清华大学出版社, 68-72.
|
林瑞泰. 1995. 多孔介质传热传质引论. 北京: 科学出版社, 21-24.
|
Alexiou P N, et al. 1990. Effect of pre-steaming on drying rate, wood anatomy and shrinkage of regrowth Eucalyptus pilularis Sm. Wood Sci.Technol., 24(1): 103-110. |
Bramhall G. 1979. Mathematical model of lumber drying Ⅰ. Principles involved. Wood Sci., 12(1): 14-21. |
DeGroot S R. 1952. Thermodynamics of irreversible processes. Am sterdam: North-Holland Publishing Company, 23~29, 111~117.
|
Gu lian Bai, P Garrahan. 1984. The temperature and moistu re content in lumber drying preheating and drying. Wood Sci.Technol., 18(2): 121-135. |
Halsopoulos G H, Keenan J H. 1981. Principles of general thermodynamics. New York: Robert E. Krieger Publishing Company, 628-643.
|
Kollman F F P, W A Cote Jr. 1968. Principles of wood science and technology I Solid wood. Berlin Heidelberg New York: Springer-Verlag, 250-256.
|
Nelson R M Jr. 1986. Diffusion of bound water in wood Part3: A model for nonisothermal diffusion. Wood Sci.Technol., 20(4): 309-328. DOI:10.1007/BF00351584 |
Nelson R M Jr.Nonisothermal diffusion of moistu rein wood.In: S chuerch C(Ed): Cellulose conference, syracuse, N.Y.New York: John Wiley and Sons, 1989
|
Nelson R M Jr. 1991. Heats of transfer and activation energy for bound water diffusion in wood. Wood Sci.Technol., 25(3): 193-202. |
Rice R W, R L Youngs. 1991. One-and tow-dimensional moisture profiles in red oak. Wood Fiber Sci., 23(3): 328-341. |
Siau J F. 1984. Transport processes in wood. Berlin, Heideberg, New York: Spring-Verlag, 25, 134.
|
Siau J F. 1983. A proposed theory of nonisothermal unsteady-state transport of moisture in wood. Wood Sci.Technol., 17(1): 75-77. DOI:10.1007/BF00351834 |
Siau J F, Jin Z. 1985. Nonisothermal moisture diffusion experiment analyzed by four alternative equations. Wood Sci.Technol., 19(2): 151-157. DOI:10.1007/BF00353075 |
Simpson W T. 1976. Effect of pre-steaming on moisture gradient of northern red oak during drying. Wood Sci., 8(4): 272-276. |
Skaar C. 1988. Wood-Water relations. Berlin, Heideberg, New York: Springger-Verlag, 3.
|
 2000, Vol. 36
2000, Vol. 36