1 问题的提出

林冠对降雨的截留涉及森林生态学, 森林气象学, 森林水文学, 水土保持等诸多方面, 是一个经久不衰的研究课题(Massman, 1983)。理论描述一般采用经验模型和理论模型(刘家冈, 1987; Liu Jiagang, 1988)两种方式。众所周知, 经验模型应用方便, 但不能反映截留与各个生态因子之间的关系; 而理论模型则可以从机理的角度来描述截留过程, 但往往计算复杂。

本文则试图寻找一种新的模型方法, 它既可以反映截留过程与各个生态因子的关系, 但又不复杂而便于计算。它部分采用理论模型的考虑, 部分采用经验模型的方法, 这就是我们所说的半理论模型。具体建模原则是, 凡是容易的部分, 都采用理论模型的考虑; 而对难以处理的部分, 则采用经验模型的方法。二者相结合, 形成一个完整的模型。需要指出的是, 本文主要研究林冠枝叶部分对降雨的截留作用。由于截留和透流是互补关系, 故本文中的透流则是完全包含了干流在内的。此外, 本文采用了许多植被辐射传播理论中的概念和方法。但是, 由于引力的作用, 降雨主要是垂直下落。只在有风的情况下, 降雨略有偏斜。被枝叶溅射的雨滴, 也有可能在一个短距离内横向飞行, 但在引力的作用下很快又回到垂直方向。因此本文主要考虑垂直下落雨滴的截留问题, 对于非垂直下落部分, 由于影响相对较小本文采用参数“等效值”的方法处理

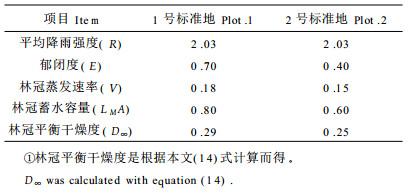
2 林冠透流率

设E为林冠郁闭度, L_M为林冠叶面指数, G为叶面的垂直投影率。仿照理论模型(刘家冈, 1987; Liu Jiagang, 1988), 定义一个干燥度D来描写林冠在降雨过程中的干燥程度, D=1代表林冠枝叶完全干燥, D=0则表示林冠枝叶处在完全饱和的吸水状态。于是对于一般状态, 林冠的透流率为

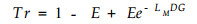
(1)

式中, L_MD代表林冠叶面指数的干燥部分, 即对降雨具有截留作用的有效部分。(1)式右边前两项1-E代表林冠未郁闭部分的透流率, 第3项表示郁闭部分的透流率, 指数部分是参考了植被辐射传播理论(Ross, 1981)中光的透过函数的形式(见图 1)。

正如“1”中所指出, 在某些情况下, 降雨偏离了垂直下落的方向, 另一方面, 由于风的作用, 叶片会在其平衡位置附近不停地摆动。因此原则上, 我们可对叶面垂直投影率G采用某种“等效值”来反映这种偏离。不过, 由于这种偏离总体来说影响较小, 故等效值与其垂直投影率差别不会太大。

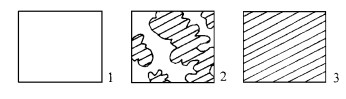
设D₀为林冠初始干燥度, 则林冠初始透流率Tr₀为

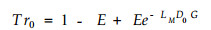
(2)

如果经过一段较长时间降雨, 林冠在截留和蒸发之间达到平衡, 干燥度也逐渐达到一个稳定值D_∞。也就是说, 林冠较干燥时, 截留较大, 蒸发较小, 林冠干燥度变小; 反之, 林冠较湿润时, 截留较小, 蒸发较大, 林冠干燥度变大。因此林冠的干燥度存在一个稳定平衡点D_∞。此时林冠的平衡透流率Tr_∞为

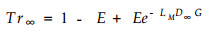
(3)

(1) ~ (3)式基本上是理论模型的考虑方法, 具有机理清楚, 定性行为合理等优点。例如从(2)式可知, 初始透流率永远小于1。但是, 初始透流率如何过渡到平衡透流率, 这是一个比较复杂的问题, 只有完全的理论模型(刘家冈, 1987; Liu Jiagang, 1988)才能描述清楚, 不过代价是计算的复杂性。本文根据经验, 用一种经验模型的方法将初始透流率和平均透流率联系起来。我们假定其过渡过程为

(4)

显然, 当t→0时, Tr→Tr₀。而t→∞时, 则有Tr→Tr_∞。式中(1-e^-βt)是一个典型的经验型的过渡因子(崔启武等, 1980)。为简便计, 本文只考虑均匀降雨的情况。记降雨强度为R, 单位叶面积饱和吸附水率为A, 则进一步我们可以假设

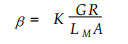
(5)

这是因为GR与林冠饱和过程正相关, 即, GR越大则林冠饱和得越快, 而L_MA与林冠饱和过程负相关, L_MA越大林冠饱和得越慢。K是一个纯粹的经验因子。(5)式的正确性和K的取值要靠实验的检验及数据的拟和。

于是(4)式便可写成

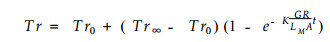
(6)

如果降雨强度R是一个常数, 则降雨量P就等于Rt, 于是

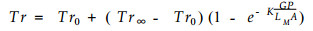
(7)

(6), (7)式便是本文的透流率半理论模型。

3 透流量

在透流率的基础上, 通过积分很容易得到透流量T

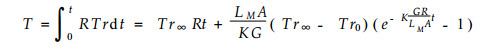
(8)

和

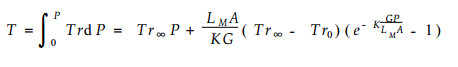
(9)

4 截留率

截留率与透流率之和为1。所以很容易从透留率求得截留率Ir

(10)

和

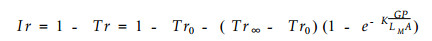
(11)

5 截留量

截留量加透流量等于降雨量。故此不难从降雨量和透流量求得截留量。

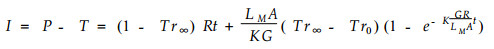
(12)

和

(13)

6 林冠的平衡干燥度

从第一节可知, 当林冠截留达到饱和时, 其平衡干燥度D_∞是一个关键参数。在我们的混合模型中, 透流率, 透流量, 截留率和截留量的表达式都离不开它。本节用一种理论的考虑和包含一定的简化, 来确定平衡干燥度D_∞。首先, 林冠达到平衡时的平衡湿度为(1-D_∞), 再乘以林冠叶面指数L_M, 郁闭度E和蒸发速率V, 即近似(忽略林冠上下部位的差别)为林冠的饱和蒸发率。另一方面, 林冠达到饱和时的截留量为降雨强度R乘以郁闭度E, 以及截留率(1-Tr_∞), 其中Tr_∞由(3)式确定。林冠饱和蒸发率应该等于林冠饱和截留率, 即, 林冠饱和瞬间蒸发强度等于饱和瞬间截留强度。于是

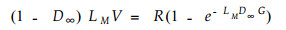
(14)

(14) 式可以确定林冠平衡干燥度D_∞。

7 与实验数据及理论模型的对比

董世仁等(1987)提供了一组关于透流率, 透流量, 截留率和截留量的实验数据, 而张学培等(1997)则用理论模型(刘家冈, 1987; Liu Jiagang, 1988)对董世仁等(1987)的实验数据进行了计算, 获得了很好的符合。在这一节中, 与张学培等(1997)一样, 我们采用董世仁等(1987)测得的生态因子, 对透流率, 透流量, 截留率和截留量进行计算。

表 1列举了部分本文有用的生态因子。

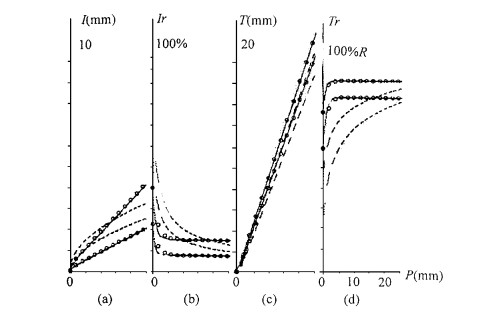
本文根据表 1的数据, 先用迭代法求得林冠平衡干燥度D_∞, 再计算出透流率, 透流量, 截留率和截留量随降雨量P的的变化。计算结果见图 2。结果表明本文模型不仅很好地符合董世仁等(1987)的实验数据, 也与张学培等(1997)用理论模型计算一致, 有基本相同的定性行为, 可以说是一个成功的模型。

(5) 式中有一个经验参数K, 在计算中我们取K=3能获得较好的符合。

8 结论和讨论

本文提出一种描述林冠截留过程的半理论模型, 它既保留了理论模型紧密联系生态因子与截留过程的优点, 又避免了理论模型往往计算复杂的缺点。该模型不仅很好地符合董世仁等(1987)的实验数据, 也与张学培等(1997)的理论模型一致, 有基本相同的定性行为。董世仁等(1987)的实测数据其实是相当分散的。图 1中的虚线实际上只是该文所使用的经验模型拟和的结果。

本文的半理论模型不但提供了一个林冠截留模型, 而且也提出了一种新的建模方法。半理论模型方法应该也可以应用于其他场合。

在(4)式中引入的经验因子(1-e^-βt)实际上是许多作者(Massman, 1983; 崔启武等, 1980)总结了大量数据后在他们的经验模型中采用的过渡形式。这是我们引用它的基础。

本文采用了植被辐射传播理论中使用已久的参数G, 植被光测学家(Ross, 1981)对各种植被的G早已积累了丰富的数据和估测方法。至于本文提出的枝叶干燥度D, 则因为是一个描述林冠干湿变化过程的中间量, 无须测量。这从(6)式到(13)式中不包含D的事实就可以看出来。