抽样调查技术是一项获取准确和可靠决策数据信息的重要工具，它是统计学领域主要的研究内容之一。由于森林资源调查的规模大、人力物力消耗大以及技术复杂程度高, 因此抽样调查方法和技术的研究和应用始终是森林资源清查中获取森林资源信息、支持以森林资源管理和信息为基础的经营规划的必不可少的重要决策工具。

抽样调查技术在森林资源调查中的应用已经有比较长的历史。传统或标准的调查方法，例如系统抽样、分层抽样、双重抽样等，大多适用于大片、连续分布的森林资源的数量和质量为主的调查目标，而且已经存在一整套成熟的抽样调查方法和技术可供选择。然而，对于稀疏、簇生、斑块状或聚集分布总体的数量和质量的调查，使用传统的调查技术和估计方法可能导致估计精度有偏和效率降低。Thompson(1990)提出了一种新的抽样调查方法——适应性群团抽样(ACS，adaptive cluster sampling)技术和估计方法，并立即受到关注，被认为是一种适合稀疏、簇生、斑块状或聚集分布总体的抽样调查方法。有关适应性群团抽样技术的概念和基本原理，已在雷渊才等(2007)一文中作了比较详细的介绍。

目前，适应性群团抽样技术进入了一个发展时期。同时，这种技术在森林资源调查、渔业资源和鸟类资源的调查也得到一些应用。至今在国际上已经出版了至少4本介绍适应性群团抽样技术的学术著作(Thompson et al., 1996；Krebs, 1999; Thompson, 2002; Williams et al., 2002)和一些研究论文。然而，适应性群团抽样技术、理论和应用等还有许多需要研究的内容。本文旨在综述当前国内外适应性群团抽样技术研究的一些重点和趋势，为进一步研究适应性群团抽样技术的理论和方法提供参考。

1 适应性群团抽样技术效率的因素配置

影响适应性群团抽样技术效率的主要因素是：1)最初抽样单元抽样方法的设计；2)网络的大小和数量；3)标准值的大小；4)邻域形状的设计；5)抽样均值及方差的估计方法和类型(Turk et al., 2005)。前4个因素是组成适应性群团抽样技术设计的主要部分，考虑到适应性群团抽样技术抽样均值估计方法和类型的特点及复杂性，本文在下节另作分析和讨论。

1.1 最初抽样单元设计的选择

从总体中抽取最初抽样单元的方法是实施适应性群团抽样技术的第一步。有许多最初抽样单元的设计方法，Thompson(1990)最早使用适应性群团抽样方法估计鸟类的分布和数量时应用简单随机抽样(simple random sampling)方法选择最初抽样样本量。之后，Thompson(1991a)应用带状抽样(strip sampling)和系统抽样(system sampling)设计方法选择最初抽样样本量，Thompson(1991b)又应用分层抽样(stratified sampling)方法抽取适应性群团抽样方法的最初样本量。Roesch(1993)、Smith等(1995)和Pontius(1997)分别使用与预估数量大小成正比的概率抽样方法(probability proportional sampling)选取适应性群团抽样技术的最初抽样单元来估计森林总体树种的分布和数量、鸟类总体数量。他们发现适应性群团抽样技术比传统的抽样技术在调查稀少、群团和聚集分布特性的总体具有更高的调查精度。Pollard等(1997)发展了线样条抽样(line transect sampling)与适应性群团抽样相结合的设计方法，随后Palka等(1999)应用这种设计方法调查估计海豚总体数量，并发现这种抽样设计方法能有效地减少估计方差和容易实施。Borkowski(1999)应用拉丁方抽样(latin square sampling)方法选取适应性群团抽样技术的最初抽样样方单元。一些研究人员应用二阶段抽样方法(two-stage designs)选择适应性群团抽样的最初抽样单元(Salehi et al., 1997; 张南松等, 2000; Muttlak et al., 2002)。

事实上，当采用方形样地的适应性群团抽样技术抽样和估计呈稀少、簇生、斑块状或聚集分布的总体时，选择一种适合的最初抽样方法是比较复杂的，因为在实施适应性群团抽样技术前并不知道那种最初抽样方法更能有效提高估计精度和抽样效率。为此，一般采用模拟分析比较的方法。为了比较选择不同最初抽样技术的设计方法以及它的效率，Christman(2000)使用模拟研究方法研究比较了3类不同网络内方差大小的稀少、簇生、斑块状或聚集的总体分布，结论是：基于设计效率和各种模拟抽样均值估计量的分布形式，分成抽样方法抽取最初抽样单元数量的方法是最好的。然而，从Horvitz-Thompson估计量方差来看，系统抽样方法选取的最初抽样单元数量的适应性群团抽样技术方差最小。

1.2 网络的大小和数量

比较适应性群团抽样技术与传统抽样技术时，一般采用Thompson等(1996)提出的相对效率(relative efficiency)指标来衡量。相对效率即为适应性群团抽样的Hansen-Hurwitz(HH)和Horvitz-Thompson(HT)估计量的方差与简单随机抽样估计量的方差之比值。假如相对效率小于1，则适应性群团抽样技术比简单随机抽样技术效率高；否则，简单随机抽样技术效率比适应性群团抽样技术效率高。由于相对效率依赖于总体的结构和分布、标准值的选择、邻域形式、样方尺寸大小、抽样设计和样本数量等因素以及这些因素相互交叉的影响，很难找到最有效率的设计。于是，Smith等(1995)和Thompson等(1996)提出了适应性抽样设计中被抽中群团内观察值的方差与总体中观察值的方差之比作为主要确定相对效率高低的指标，从而决定何种抽样设计效率更高。它的大小取决于网络内方差与总体方差的比值和最终抽样样本数量与最初抽样样本数量的比值。考虑到网络内方差值和最终抽样样本量与最初抽样样本数量不容易理解，一般应用总体中网络大小和数量的概念来评价相对效率, 即b(n₁, m, N)＝m/n₁[(N-n₁)/(N-m)]。当b值减少，适应性群团抽样比传统抽样技术相比较效率增加；当最初抽样单元n₁和总体单元N一定，相对效率b随着网络单元数m增加而提高。

Brown(2003)应用泊松群团分布过程(poisson cluster process)模拟研究了总体目标观察值为200的不同群团数量(例如总体群团数分别为λ₁＝5，10，…, 100个群团)和不同群团的大小(例如每个群团数量分别为λ₂＝10，20个目标观察值/每个群团)的情况。模拟的结果表明：随着总体观察值增加，网络数量增加并达到最大，然后逐渐减少。发生这种情况是由于超网络现象(hypernetwork)出现的结果。超网络是指占主导地位且具有高的入样概率的网络。也就是说，随着总体群团数λ₁增加，相邻网络开始合并而形成更大的网络，结果导致总体中网络数减少。除了总体的空间结构和分布影响网络的大小和数量外，网络的实际数量还与标准值的大小和邻域形式的选择有关。

Brown(2003)应用相对效率指标研究评价总体网络数量和大小分布的规律，结果表明：网络数量增加，适应性群团抽样设计的Hansen-Hurwitz估计量的相对效率值减少，并小于1。但是当网络数量有一个迅速的增加时，相对效率减少更大。网络数量多且聚集紧凑的总体与网络数量少且分散的总体相比较，前者的Hansen-Hurwitz估计量的相对效率比后者高。

如果网络大，最终抽样与最初抽样的样本数量的比值增加，相对效率减少。另一方面，如果网络大，网络内将有更大的方差，相对效率可能会提高(Brown, 2003; Christman, 2000)。Brown(2003)提出最初抽样样本数量和网络内方差是影响相对效率的一对相互矛盾的因素。就抽样单元数来说，假如具有大的网络，最终抽样单元数量与最初抽样单元数量的比例增加，结果减少相对效率值。但是，大网络有更大的网络内方差，结果是相对效率值增加。因此，Brown(2003)模拟研究的最后结论为：2至4个单元组成的网络能得到最高的相对效率。

1.3 标准值的选择

在实施适应性群团抽样技术前，需要选择增加邻域单元的标准值。标准值的大小直接影响网络的大小以及抽样效率。然而实际实施抽样工作过程中，选择一个适合的标准值是比较困难的。Christman(1997)研究了不同标准值和不同估计方法的抽样相对效率。当标准值C=1时，Horvitz-Thompson估计量比简单随机抽样方法效率高；当采用一次邻域形式，并取标准值C=5时，Horvitz-Thompson估计量的效率比简单随机抽样方法差。当网络内方差占总体总方差很高且采用一次邻域形式时，Hansen-Hurwitz估计量比简单随机抽样方法效率高。但是标准值C＝5与C＝1相比时，前者的Hansen-Hurwitz估计量的效果比后者效果更好，原因可能是取大的标准值有更多的限制条件而导致网络内变异减少。

Brown(1996)分析了不同标准值和不同密度总体的适应性群团抽样技术的相对效率。当估计高密度分布的总体时，标准值C＝2的相对效率优于C＝1，原因是选取大的标准值减少了网络的大小，结果可以减少边缘单元的数量。当估计低密度的总体，标准值大的相对效率比标准值小的相对效率更差，原因是选取大的标准值会有更少的抽样单元满足条件或被选择，而形成了很小的网络。

Christman(2000)的研究表明：在相同的最初抽样样本数量，与简单随机抽样技术相比较，适应性群团抽样技术的效率与标准值大小的选择成反比，即随着标准值选择的增加，网络内的方差减少。因此，为了控制总样本数量，选择相对大的标准值将会减少适应性群团抽样技术的效率，而且边缘单元的样本可能包含非零的观察值。这种现象是应用适应性群团技术估计稀少和群团分布的总体密度时不愿遇到的，因为它损失了非零观察值单元的信息。然而，Smith等(2003)的研究结果表明：提高标准值不是控制总样本数量的一个实际可行的方法，他们认为提高标准值的效率是不可预见的结果。

选择小的标准值可能导致更大但更少数量的群团结构；选择大的标准值可能导致更小但更多数量的群团结构。因此，标准值的选择依赖于抽取少量而大的群团还是抽取许多小的群团所付出的代价(Brown，1994)。

在一个模拟研究中，Brown(2003)选择了2个标准值(即C=1和2)，适应性群团抽样的Hansen-Hurwitz总体均值估计量都比简单随机抽样方法的效率高。考虑到更小的总体(即更少的网络数量)，标准值C=1的适应性群团抽样的Hansen-Hurwitz估计量比C=2的效率更高。然而，在更大的总体中(即更多的网络数量)，选择标准值C＝2比C＝1的Hansen-Hurwitz估计量更好。这说明标准值和网络数量有交互作用。

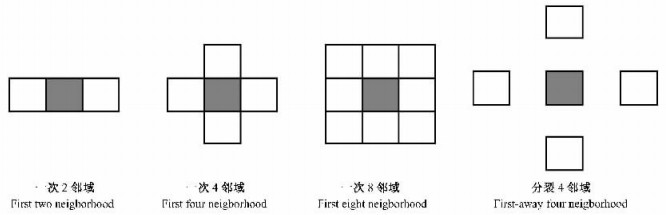
1.4 邻域的形状和设计

适应性群团抽样设计中有多种样地形式的取样，包括样方、样圆、样点、样线和样带等。不同样地的形式导致不同的邻域形式。实践中考虑到方形样方易于操作和应用，方形样方被广泛采用。方形样方的邻域形式灵活并具有多种形式，目前一般使用如图 1所示的几种邻域形式。

改变邻域的形式能够将抽样的焦点问题转变为群团之间或群团内的问题(Brown, 1994)，这说明了邻域形式的设计是适应性群团抽样技术中非常关键因素之一。Christman(1997)使用三类邻域形式的设计测试和评价了几种不同总体分布的适应性群团抽样的结果，表明最有效的适应性群团抽样设计是使用单元相毗邻的邻域设计，例如一次邻域形式。Christman(1997)也建议使用非毗邻(noncontiguous)[或分裂4邻域(four-away)]的邻域形式。但是，这种邻域形式设计的不同模拟总体和不同最初抽样样本的适应性群团抽样的Hansen-Hurwitz估计量和Horvitz-Thompson估计量的方差都比简单随机抽样估计量的方差大。

也有研究结果表明：一次2邻域可能比通常的一次4邻域形式的适应性群团抽样设计效率更高(Christman, 1997)。因为设计抽取2个单元的一次邻域的形式而不是4个单元的一次邻域形式将使样本量减少。考虑到抽样成本，2单元的一次邻域设计可能更具有吸引力。如果总体中的群团分布具有某一特定分布的方向，邻域的形式应该反映所期望的方向设计(Christman, 2000)。Brown(1996)比较了一次4邻域和一次8邻域形式的适应性群团抽样设计，发现前者具有更高的适应性群团抽样的相对效率，很明显这是因为一次4邻域比一次8邻域的设计有更少的边缘单元数。在另一个模拟研究中，Brown(2003)的结果说明：实际的网络数量取决于邻域定义的形式。作者考虑了一次8邻域、一次4邻域和一次2邻域等3种邻域定义形式，结果表明：网络数量是随着邻域定义的单元数量减少而增加。这说明使用小量的邻域单元形式能提高含有大量观察值分布的网络总体抽样的相对效率；相反，具有小量观察值分布的网络总体的相对效率则减少。Salehi等(2005)认为：1)不适合的邻域设计将会导致选择过多的边缘单元(edge units)；边缘单元是不满足标准值条件的邻域单元，而过多的边缘单元不但会增加调查成本，而且也不能提高HH和HT估计精度；2)实际的抽样调查过程中调查所有的邻域单元是非常困难的；3)实际抽样调查过程中定义一种邻域也是非常困难的。所以Salehi等(2005)提出了二阶段序贯抽样设计，在这个抽样设计估计过程中不考虑邻域单元。

2 适应性群团抽样的设计和估计方法

使用适应性群团抽样技术调查稀疏、簇生、斑块状或聚集分布总体的实施过程中，首先，考虑最初抽样单元的设计和标准值的确定；其次，考虑邻域形式的设计和选择；最后，就是用什么估计方法估计适应性群团抽样样本均值和方差。由于不同的最初抽样单元的设计、标准值的大小和邻域形式的设计，因而会导致许多不同的适应性群团抽样技术设计以及不同的估计方法。本节主要回顾一些具有代表性的适应性群团抽样技术的不同设计和估计方法。

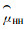
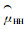
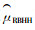
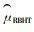
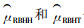
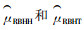
基于传统的Hansen-Hurwitz和Horvitz-Thompson估计量, Thompson(1990)考虑到使用Horvitz-Thompson估计量时边缘单元的不确定性和Hansen-Hurwit估计量的复杂计算，对适应性群团抽样技术的估计方法提出了修正的Hansen-Hurwitz()和Horvitz-Thompson()2个无偏估计量。考虑到 和 不是最小充分估计量的函数，Thompson(1990)又提出了Rao-Blackwell理论的Hansen-Hurwitz()和Horvitz-Thompson ()2个无偏估计量, 并用实例比较了 估计量，发现前者具有更小的估计方差。但是，Thompson(1990)没有给出计算 估计量算法的适合方法，这是因为Rao-Blackwell理论的复杂和计算量大。为了解决此问题，Salehi(1999)导出了容易计算 的算法，并用实例说明了2个估计量算法的详细计算过程。

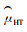
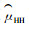
大多数比较2个无偏估计量的研究结果表明：修正的Horvitz-Thompson()估计量优于修正的Hansen-Hurwitz()估计量(Salehi，1999；2003)。Christman(1997)也使用模拟研究方法比较修正的Hansen-Hurwitz和Horvitz-Thompson估计量的效率和方差，结果表明：大多数模拟的研究情况，修正的Horvitz-Thompson估计方法具有更小的方差，但它对抽样条件和抽样总体结构的改变更为敏感。因此，Christman(1997)建议，当使用修正的Horvitz-Thompson估计方法估计抽样均值和总体时，如果潜在的耗费存在，应该仔细规划抽样设计。在实际抽样过程中，虽然修正的Horvitz-Thompson比Hansen-Hurwitz估计方法具有小的估计方差，但考虑到修正的Hansen-Hurwitz估计方法计算容易和方便，因此它仍被广泛应用于适应性群团抽样估计计算。

最初抽样设计方法、标准值、邻域形式和估计方法等因素的不同组合将会导致大量不同的适应性群团抽样设计。实施适应性群团抽样技术遇到的主要问题是最终抽样样本量的随机性或不确定性，因为最终抽样样本量的随机性或不确定性使得人们在调查前无法确定最终抽样样本量以及抽样调查的成本，而这些正是在作调查计划前需要了解的，特别是抽样调查费用昂贵或费用有限时就显得更为重要。因此，为稀疏、簇生、斑块状或聚集分布的总体设计一个有效的抽样方案并为不同抽样设计方案提出无偏估计量是一项非常具有挑战性的研究任务。

为了有效解决适应性群团抽样方案的设计问题，有研究者提出使用一定条件来限制适应性抽样最终网络单元数量以减少抽样工作量和成本。Thompson等(1996)建议了一些方法来限制总的抽样成本。他认为假如在抽样过程中很明显地知道最终抽样样本数量很大时，就停止继续适应性群团抽样的方案，对仍未调查的区域只选择最初抽样中的样本数量。这样的结果有效地将调查研究的区域分成适应性抽样层和非适应性抽样层。但是，使用2种技术在同一抽样研究区域将会有不同的抽样密度，这种抽样设计方法是不可取的(Brown et al., 1998)。

另一种抽样设计方法是选择适合的标准值来限制最终抽样样本数量以确保由最初抽样设计所产生的群团不要太大。为此，Thompson等(1996)提出：在开始抽样时，如果适合的标准值不能确定，可以按2步进行抽样设计。首先，观察最初抽样单元的目标值；然后，在第一步所观察到的目标值的基础上确定增加邻域单元的标准值大小，标准值的确定将确保邻域单元数以固定的比率增加。这种设计方法的不足是需要在最初抽样单元中不断重复(Brown et al., 1998)。

限制最终样本量最常用的一种设计方法为叫停规则(stopping rule)的方法。图 2是被广泛使用的一个样方单元的一种叫停规则设计图。图 2(Su et al., 2003)中O为样方最初抽样单元，S1，S2和S3分别为一阶、二阶和三阶叫停规则，灰色的样方单元为边缘单元，邻域形式设计为一次4单元。在适应性群团抽样研究领域中，叫停规则的使用引起了广泛的关注和重视。尽管它的使用在适应性群团抽样调查中能减少最终抽样样本数量，然而，叫停规则的使用可能导致网络重叠和不固定，因而在叫停规则情况下的HH和HT估计是有偏的，但有偏的程度可能不是太大，主要依赖于抽样如何实施(Brown et al., 1998)。Brown(1994)最早使用叫停规则(S＝1, 2和3等步数)来限制最终抽样样本数量，或叫限制性适应性群团抽样(restricted ACS)设计，并研究了适应性群团抽样估计的特性。这种限制性的适应性群团抽样设计是：首先确定样本数量；然后以序列的方式(sequential fashion)选择最初抽样单元直至到抽样单元等于或大于抽样前确定的样本数量时就停止。作者没有提出有效的估计量，而是采用修正的HH和HT估计量。Hanselman等(2003)也使用了叫停规则来限制最终抽样样本数量。虽然叫停规则起到了限制最终抽样样本的数量，但是在大多数情况下，修正的HH和HT估计量导致了有正的偏估计(即估计偏高)，而且最终抽样样本数量仍然具有随机性(Salehi et al., 2002)。此外，叫停规则的使用包含了边缘单元，修正的Hansen-Hurwitz和Horvitz-Thompson估计方法对这种抽样设计的估计有偏是因为估计中没有使用它。为了估计修正的HH和HT估计量有偏数量的大小，Brown等(1998)使用Bootstrap方法估计偏的数量，并认为Bootstrap方法能调整修正的HH和HT估计量在限制性群团抽样设计中的有偏估计。限于篇幅，如何使用Bootstrap方法计算详见Brown等(1998)。

由于叫停规则的使用导致修正的HH和HT估计量为有偏的估计，所以目前许多研究人员研究如何修正限制性的适应性群团抽样设计技术和估计方法为无偏估计。

Lo等(1997)使用了一种限制性ACS抽样设计，即采取限制每个网络样本数量。他们将这种抽样设计用于调查和估计太平洋鳕鱼总体数量，与没有限制的适应性群团抽样估计结果进行比较，尽管HT和HH方法估计方差减少了，但估计的结果是有偏的。Salehi等(1997)提出了二阶段适应性群团抽样设计(two-stage ACS)，即次级抽样单元(secondary unit)的邻域单元被限制在由最初抽样方法抽取的一级抽样单元(primary unit)内。尽管作者发展了总体均值的有效估计量，但是，这个抽样设计的缺陷是：包含有更多单元且位于2个一级抽样单元之间的一个群团不能完全被抽样。Su等(2003)使用泊松群团分布模拟的方法产生三类不同集群的总体(即以变异系数大小表示的低中高)，采用次序统计量(order statistics)，从最初抽样样本观察值(y₁≤y₂…≤y_n1-r…≤y_n1-r+1…≤y_n1)中确定标准值为C＝y_n1-r，并联合使用不同叫停规则(例如S1，S3和S5)来评价适应性群团抽样效率。他们发现偏的估计大小与序统计量、叫停规则的步数和总体空间分布有关。如果总体集群程度高、叫停步数小和次序统计量大，叫停规则导致相对大的正偏HH估计量。但是，HT估计量的偏对叫停规则的使用不太敏感，在比较小的次序统计量条件下，使用叫停规则可以减少HT估计量的偏。因此，在使用叫停规则情况下，HT估计量是偏好的。对于高集群的总体，如果将使用与不使用叫停规则进行比较，叫停规则的使用将会减少HH和HT估计量的效率。

Christman等(2001)认为限制性的ACS方法在稀少分布总体的抽样中可能不会产生足够量的或大量的样本量，所以他们提出了逆的ACS(inverse adaptive cluster sampling，IACS)抽样设计。这种设计方法是预先规定最初抽样单元数中非零观察值的样本数量，如果非零观察值的样本容量不满足预先确定的数量，则继续抽样直至条件满足时停止。因此，最初抽样单元形成的网络数小于或等于最初抽样单元数。例如，考虑一个总体的分布为Y=(0, 0, 0, 0, 10, 40, 0, 0, 5, 20, 60, 0, 0, 0, 0, 0, 0, 0, 0, 0)。由此得知：总体Y由N＝20个单元组成(即y₁, y₂, …, y₂₀)，非零观察值(y)为M＝5个(即组成2个非零观察值网络：y₅=10和y₆=40；y₉=5，y₁₀=20和y₁₁＝60)，总体观察值T＝135。假设适应性群团抽样的标准值C＝(y:y>0)，最初抽样单元数为n₁=5，随机抽取了(y₁=0, y₃=0, y₇=0, y₉=5, y₁₅=0)；又设预先确定的非零观察值样本数量k=2个。由此可知：第一次的5个最初抽样单元数不满足预设的条件是k=2。因此，继续使用简单随机方法抽取一个样本单元y₄=0，仍不满足条件，则需要继续增加一个样本，假设再随机抽取y₁₁=60，则满足叫停规则。适应性群团抽样的最终网络数和对应的观察值为(y₁＝0，y₃＝0，y₇=0, y₉=28.33, y₁₅=0, y₄=0, y₁₁=28.33)。这种方法的合理性是：选取满足条件(非零值)的最初抽样单元，然后通过叫停规则可以达到控制抽样单元数和避免估计值为零的单元数。在这种抽样设计条件下，修正的HH估计结果是正的偏。Rocco(2003)发现使用逆的ACS抽样设计时不满足非零观察值条件的单元在最初抽样单元过程中被抽中的概率高，从而会导致抽样效率低。因此提出限制性的逆ACS(constrained inverse ACS or CIACS)抽样设计。这个抽样设计方案是：1)如果最初抽样单元中至少2个单元满足非零观察值的单元存在，然后按照适应性群团抽样过程进一步实施；2)否则，抽样过程继续至到2个单元满足条件为止。后一种抽样过程有2个方法处理最终抽样单元数，一是保留最后满足条件的一个单元的最终样本数量(Sⁿ)，二是拒绝最后满足条件的一个单元的最终样本数量(Sⁿ⁺¹)。然后使用Rao-Blackwell理论分别估计2个最终样本量，得到它们的估计均值。与逆ACS设计比较，CIACS效率更高。

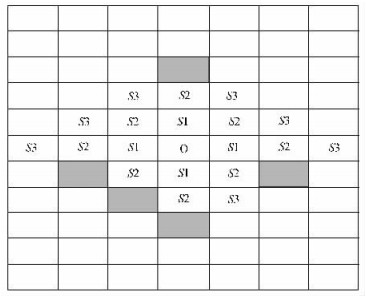
叫停规则、逆的适应性群团抽样和限制性的适应性群团抽样设计的目的是为了控制最终抽样单元数量，虽然这些抽样设计方案能够达到此目的，却违背了在适应性群团抽样估计中修正的HH和HT估计量将总体进行唯一网络划分的假设原理，因而可能产生有偏的估计。Salehi等(2002)为了解决限制性的适应性群团抽样HH和HT估计的有偏性，应用Brown等(1998)的限制性ACS方法进行模拟研究，基于修正的Rao-Blackwell理论和Murthy估计量，提出了使用包含边缘单元的两种无偏估计方法，并用实例比较了修正的HH和HT估计量，结果表明2种新的估计量优于修正的HH和HT估计量，并有更小的均方误差(MSE)。但是，Salehi等(2005)为了避免使用选择过多且不能提高估计精度的样本数量——边缘单元，提出了二阶段序贯抽样设计(two-stage sequential sampling)。图 3展示二阶段适应性群团抽样设计过程(Sakhi et al. 2005)。首先，确定标准值C＝10，将总体所有单元分为8个一级单元(primary units)分别在图左右两边用1, 2, …, 8标记，并按照简单随机抽样方法抽取4个一级单元(例如，图中1，3，5和6一级单元)；然后，在每个一级单元内按照简单随机抽样方法抽取2个单元(例如图中浅灰色单元)；最后，在抽取的4个一级单元按照C＝10再按照简单随机方法抽取4个单元(例如图中的深灰色样方)。这种抽样设计不考虑边缘单元，显然，它比传统的抽样设计和限制性的其他适应性群团抽样设计效率高，特别适合于抽样调查费用高的研究区域。在Murthy(1957)估计量的基础上，他们导出了修正的无偏估计量。这种抽样设计也被称之为广义的逆ACS(general inverse sampling design)抽样设计。

Chao等(2003)对适应性群团抽样技术进行了修正，提出了不完全适应性抽样设计技术(incomplete adaptive cluster sampling)。

从上述的研究实例可以看到，如何选择适合的条件是实施适应性群团抽样技术的关键问题，因为它关系到抽样效率高低和最终抽样样本数量(Smith et al., 1995；Brown，2003)。假如选择的条件太自由和宽松，适应性群团抽样技术的样本数的扩展频率将会提高，这样会导致最终抽样样本数量太多而难以完成抽样调查工作。相反，条件限制太严，可能会导致样本量太少而不能达到期望的抽样精度。

3 适应性群团抽样技术的应用研究

Thompson(1990)第一次提出适应性群团抽样理论和方法到报道该技术方法在生物学领域资源调查中的应用只有十几年(Roesch，1993; Brown，1994)。尽管自适应群团抽样技术在生物学领域和林业抽样调查中应用研究不多，但是应用研究的发展速度很快，应用的行业也在逐步扩大和推广。

Lo等(1997)使用限制性ACS调查估计太平洋沿岸鳕鱼总体数量。他们的研究结论为使用该方法调查比传统的调查方法更加容易实施，而且估计精度更高。此外，该方法还能提供相关的和非常有意义的生物学特性信息，例如调查研究区域内鳕鱼聚集斑块的大小和数量等，这些信息对于区域内生物多样性的研究很有指导意义和帮助。

Strayer等(2003)应用ACS抽样方法调查贻贝密度。他们首先使用简单随机抽样方法布设样地, 最初抽样的样方面积确定为0.25 m²，并选择十字形状的邻域形式。因为在最初抽样的样方中存在不同类型的贻贝分布和数量，而且为了比较快速地评价研究区域内贻贝的分布密度，所以他们采用了不同样地使用不同的标准值来增加邻域单元数量。

McDonald等(1999)使用最初样条样方(line transect sampling)的ACS抽样技术调查北极熊数量和分布。他们设计样条样方的长为37 km，邻域确定为在平行样条样方两侧9 km处。他们发现在5个最初样条样方内满足条件，但是适应性群团抽样过程中的样条样方内不满足条件。

Palka等(1999)联合使用ACS和样条样方抽样方法调查海豚数量，结论是在野外调查区域容易使用两种联合抽样方法布设样地，与传统的样条样方抽样方法比较，联合的抽样方法可以获取更高精度的密度估计。

张南松等(2000)在研究农作物害虫种群分布时提出了二阶适应性群团抽样技术调查害虫的密度，并从理论上证明这种抽样设计是一个无偏估计，方差也比较小，在害虫种群管理上有一定的实用价值。

Conners等(2002)在伊利湖使用样条样方的ACS调查一种红纹鱼。他们认为：ACS抽样设计可行，但是指出了几个问题。一是评价条件(即标准值)实时数据的处理；二是正确地选择适应性单元的地理参考位置；三是为了控制最终抽样单元数量的有效条件和邻域形式。

Hanselman等(2003)应用ACS抽样技术调查美国阿拉斯加海湾的石鱼数量。他们基于以往调查数量的百分位确定标准值，在相邻的2个拖网之间的距离确定为0.1海哩(185.2 m)，并使用叫停规则加以限制最后抽样样本数量。他们分别评价了不同鱼种分布和标准值的效率，并且比较适应性群团抽样和简单随机抽样技术，结论是适应性群团抽样技术比传统的抽样调查技术更加有效。

Smith等(2003)在24个不同的野外研究区域使用ACS技术调查贻贝的密度。他们用系统抽样调查方法设计最初样方单元，标准值设定为种的存在，并且邻域形式设计为标准的十字形状。当最初样本量等于最终样本量，他们比较了ACS抽样技术和系统抽样调查技术，发现ACS抽样技术有更小的抽样误差。虽然ACS抽样技术增加了抽样单元数量，但提高了稀少物种探测性的概率。

Noon等(2006)研究印度南部热带雨林陆地爬形动物，为了评价群团抽样技术在估计动爬形物种组成和密度，他们首先使用样地面积为25 m²的简单随机抽样技术，并且发现大多数样地没有爬形动物出现和一些样地只出现爬形动物聚集分布的情况。为了提高抽样调查效率和得到更精确的爬形动物密度的估计，他们改变抽样方法，使用了适应性群团抽样技术进行抽样调查。最后比较2种抽样技术的效率和探测稀少物种的能力，发现ACS技术未能获取比简单随机抽样技术更高的密度估计精度。但是，ACS技术能探测更多的稀少物种的分布和组成。

适应群团抽样技术在调查呈稀少和簇群团状分布的总体表现出了很多有利的特性, 而且目前正被广泛应用于动物、鱼类等资源调查。但这项抽样技术在呈稀少、群团的植被和森林资源调查以及估计总体密度的应用仍然很少。根据我们最近整理统计的几个主要国际林业学术刊物(Forest Science、Forest Ecology and Management和European Journal Forest Research等)关于适应性群团抽样技术研究的论文数量和引用情况, 可以看出至今只有很少一些植被和森林资源以及森林中的其他资源调查应用适应性群团抽样技术。

Roesch(1993)是第一个将在林业广泛使用的预估数量大小成正比例的概率抽样方法(PPS)与ACS技术结合，发展了森林调查系统，并用点抽样模拟了3.1 hm²混交林分树种密度。他验证了ACS的潜在效率，特别是估计方差比传统的抽样方法小，但是他也指出：由于增加的抽样样本数量可能会导致成本增加的风险存在。

Acharya等(2000)在尼泊尔一个40 hm²的生态保护区成功地使用ACS技术调查了3个稀少树种。他们首先使用系统抽样方法选择最初抽样单元，然后使用ACS技术以最初单元确定在3个树种中任何一个树种的直径≥12 cm为增加邻域标准条件，邻域的形式选择为十字形。他们使用简单随机抽样估计方法、修正的HH和HT估计方法，结论为：使用系统的适应性群团抽样技术(SACS)比传统的系统抽样技术更有效率；稀少树种呈现大的群团分布比小的群团的分布的情况下，这种技术的使用效果更加明显。

Talvitie等(2005)为了调查赫尔辛基市所属的3 700 hm²森林公园内的枯损木数量，使用了简单随机抽样和ACS抽样技术。在抽样设计过程中他们只选择了大于5 hm²的林地作为调查研究对象，使用半径为19.95 m的圆形样地并使它位于0.25 hm²方形的遥感图像单元中心。采用系统抽样方法抽取61个最初圆形样地，在圆形样地中枯损木直径以2 cm径阶进级测量，枯损木等级则按照0~9数字确定。等级的定义是依据枯损木蓄积或断面积占样地蓄积或断面积的比例。标准值的确定为大于枯损木等级1，满足条件则在最初样地的东西南北方向增加4个邻域样地。他们比较了传统抽样方法与ACS方法的效率，同时在ACS抽样设计中比较了不同标准值(即枯损木等级1和2)的抽样效果，结果是：ACS抽样技术效果优于传统抽样技术，而在标准值为2的HT估计量比标准值为1的估计量好。

加拿大森林采伐一般采用小面积皆伐方式，因此了解估计国家和区域内由于小面积皆伐方式而形成的斑块面积对森林生态系统可持续经营是非常必要的。为了调查估计国家的和区域的采伐率和采伐斑块面积，提高这种特殊分布总体的抽样效率和估计精度，需要选则可行有效的抽样设计技术。Magnussen等(2005)使用了简单随机抽样方法和适应性群团抽样技术调查采伐斑块面积，他们模拟了总和面积为364万km²，在平均10年间以从0.2%到2%的采伐率变化，共有78~10 742个不同大小和形状的采伐斑块。估计结果是：ACS技术估计的标准差比SRS技术减少了30%~50%，此外研究表明：包含太大的采伐斑块的总体不宜使用ACS技术。

Philippi(2005)使用ACS抽样技术研究调查几种分布稀少的草本植被分布数量，并比较了1和4 m²不同大小的最初抽样单元的ACS抽样效率以及HH和HT不同估计方法的估计精度。他研究的结论为：HT估计方法的方差小于HH估计方法。1和4 m²的最初样方单元设计都表现为合理的估计结果，但是前者抽样数量占总体植被数量的30%~36%, 面积仅占5%；后者植被数量和面积分别为78%和21%。

4 适应性群团抽样方法和技术的研究展望

适应性群团抽样方法和技术的理论的提出毕竟只有十来年，有许多理论上的和实践上的问题需要进一步研究探讨，使之不断改进和完善。正如前面所叙述，适应性群团抽样方法和技术的主要缺点是事先无法确定最终抽样强度。目前解决的主要方法是采用抽样设计、标准值(预设值)和叫停规则等来限制最终抽样强度。那么这些规则如何确定才能使抽样工作量减少和估计值无偏以及估计精度提高？此外，适应性群团抽样技术的Hansen-Hurwitz(HH)和Horvitz-Thompson(HT)估计量的置信区间估计采用传统的简单随机抽样方法计算是否合理？适应性群团设计的抽样总体分布是非对称的和不连续的(Christman，2000；Christman et al., 2001)，因此，理论上适应性群团抽样设计使用简单随机抽样正态分布假设的置信区间估计方法是不适合的。目前，Christman(2000)使用自助法(bootstrap)计算2种估计量的总体置信区间。所有这些，理论上非常需要研究和探讨。同时，实践上应用适应性群团抽样技术和方法时样地设计的大小、形状和结构以及此相应的估计方法也需要进一步研究。

我们已经知道在使用ACS抽样技术前应该对所要调查的总体进行仔细地研究，能否通过模拟研究对影响适应性群团抽样技术的因子水平的确定提出一套有指导性的规则或框架，以便调查人员能方便操作和顺利实施这种抽样调查技术，例如提出我国沿海红树林种群群团分布数量的调查、西部沙漠地区稀疏植被的调查技术规程或建议等。Smith等(2003)建议通过试验性的模拟研究(a pilot study)针对不同总体分布、不同最初抽样设计、不同网络大小和数量、不同标准值条件和不同邻域形式的抽样设计，以及这些不同抽样设计所产生的抽样均值方差和抽样成本，提出一套适合不同种群和植被的实际情况的适应性群团抽样设计规程和技术设计标准及体系。这方面的研究工作任务艰巨，研究成果在实际的抽样调查工作中非常需要，也是我们今后研究和发展的主要方向。

此外，开展模拟研究工作没有适合的统计分析模拟软件几乎是不可能获取抽样统计分析结果和指标的。因此，模拟软件的研制，特别是界面友好型的模拟软件的开发是研究和推广适应性群团抽样技术的必不可少的手段和工具。目前美国Battelle Memorial研究院开发了模拟软件VSP(visual sampling plan)，它对抽样模拟设计很有帮助(Smith et al., 2004)。但是该软件在适应性群团抽样技术设计中只包含简单随机抽样方法抽取最初样本和一次2邻域形式的模块，没有叫停规则和不同标准值等内容的模块。Smith(2007)最近开发了一个比VSP软件功能更强大的模拟软件系统，它将为应用适应性群团抽样技术模拟研究提供一个更好的平台。