文章信息
- Zhang Dongyan, Liu Yixing, Cao Jun, Sun Liping
- 张冬妍, 刘一星, 曹军, 孙丽萍
- Neural Network Prediction Model of Wood Moisture Content for Drying Process
- 干燥过程中木材含水率神经网络预测模型
- Scientia Silvae Sinicae, 2008, 44(12): 94-98.
- 林业科学, 2008, 44(12): 94-98.
-
文章历史
- 收稿日期:2008-01-24
-
作者相关文章
Some complicated processes such as wood drying are difficult to establish effective drying mathematical model because of strong nonlinear, large lagged and time varying. So far only few satisfying drying automatic controlling systems have been realized. The principal problems to realize fully automatic controlling of drying are mathematical modeling and carrying out drying schedule, which will influence speed and energy consumption of wood drying directly. In recent years, the studies of the modeling of drying mainly focused on the mechanism models. Hu(1997) researched drying schedule model based on conventional regression method. A formulation of a dynamic, kiln-wide drying model was described by Sun et al. (2000), and the model solved the unsteady-state mass, momentum and energy balance equations for both the airflow and the wood boards, so as to get wood temperature and moisture content. Analyzing moisture transfer and wood structure, Carlsson et al.(2000) established a two-dimensional, orthotropic model to create effective drying schedules for the mixture of boards with distribution of sapwood and heartwood. Hukka (2000) studied a two-dimensional model for the stress analysis of drying wood, which can describe viscoelastic-mechanosorptive-plastic behavior, to predict deformation and optimize schedules. Cronin et al.(2003) presented single set point and double set point schedule models, and contrasted the Monte-Carlo model to analyse and optimize wood drying schedules. A wood drying model was developed by Fortin et al. (2004) to simulate the convection batch drying of lumber at conventional temperature based on the water potential concept, and the model could compute the average drying curve, the internal temperature and moisture content profiles, and the maximum effective moisture content gradient through the thickness of board, so as to optimize drying schedules. However, most of these models are difficult to actualize in practical control due to the fact that too much restrained conditions makes the models very complex, or very simple conditions makes the models inaccurate. Artificial neural networks can offer a very effective way for system identification, especially for nonlinear dynamic system identification and prediction due to their capability of strong learning, characteristic of nonlinear transform and capability of parallel processing(Wang et al., 1996; Xu, 1999; Wu et al., 2001). This paper used time-delay neural network, the non-traditional and black box express tool, to describe complicated wood drying, so as to realize identification of model and prediction of wood moisture content. All these offered effective rules for realizing automatic control and improving quality and output of wood drying.
2 Identification for schedule model of wood drying 2.1 Schedule model of wood dryingThe first problem to solve is how to transform drying schedule table to effective mathematical model in using computer to control wood drying. Moisture content schedule is used extensively both at home and abroad presently. According to MC drying process can be divided into several stages. There are corresponding temperature and humidity of medium at every stage. So the drying schedule model was established in this paper, namely the relation among temperature, humidity and wood moisture content. Because it was a non-linear dynamic system, the paper adopted time-delay neural network to establish model of wood drying.
2.2 Time-delay neural networkThere are two methods for dynamic system identification:one is introducing system dynamics characteristic directly to network, such as the recurrent network model and the dynamic neuron model, the other is considering dynamic factors in network input signals, namely adding lagged signals of input and output to input of network, which ensures that the output of network contains previous information of input and output, so as to simulate the discrete dynamic system(Narendra et al., 1990; Kaiser, 1994; Palancar et al., 2001; Shi et al., 2002). This paper adopted the second method.
Time-delay neural network introduced tapped-delay-line to feed-forward neural network (multi-layer BP network, RBF network and CMAC network), which can be described as:

|
(1) |
In fact, Time-delay neural network can solve dynamic problems using static network. To describe the dynamic time-list can be solved by spreading the input signals simply according to time-coordinates. All the information spread is regarded as the input mode of the static network. In other words, time is regarded as another-dimensional signal to be added to the import of neural network simultaneously to approach dynamic time-list system by the static network. In this way the time information of the neural network can be emphasized adequately. But in fact, the input time-list can only be spread to limited-dimensional input signals. Because there is no feedback, its training method can apply traditional BP learning algorithm totally.
2.3 Neural network identification for drying schedule modelFor the relation between the input-output of neural network (model P') and the identification system (model P), there are two identification structure:parallel linking type and series-parallel linking type, which separately corresponds to the parallel model (PM) and the series- parallel model (SMP)(Xu, 1999). The series-parallel model (SMP) is obtained by time-delay neural network (Fig. 1) and described as (2).
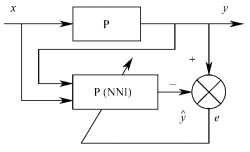
|
Fig.1 Identification structure ofseries-parallel model |

|
(2) |
The output at moment k depends on the input and output of the system before the moment k. Because the series-parallel structure trains the network by regarding the input and output as the identification information synchronously, it is possible to assure the constringency and stability of the identification model. Thus this structure is frequently adopted.
The identification structure of drying schedule model (the relation model among temperature, humidity and wood moisture content in drying kiln) based on time-delay neural Network is shown as Fig. 2. The structure identification of multi-input and multi-output system involves fixing rank, namely defining m and n in (1), which was not discussed in detail because it was very complicated. According to the practical experiment n was equal to 2, m was also equal to 2 in (1) in modeling, which was equivalent to have 8 input nodes and 1 output node. Temperature x1 and humidity x2 were the inputs of system. MC y was the output of system. x1(k) and x2(k) showed the present state. x1(k-1), …, x1(k-n), x2(k-1), …, x2(k-n) showed the historical state of input. y(k-1), …y(k-m) showed the historical state of output. yN was the output of the time-delay neural network. So the model of drying schedule could be described as:

|
Fig.2 Time-delay neural network identification for drying schedule model |

|
(3) |
We carried on experimental analyses of three species:Fraxinus mandshurica, Betula platyphylla and Xylosma racemosum. A downscaled industrial drying kiln with dimensions of 1.8 m×1.7 m×1.2 m was used in this study. In the kiln, the temperature, humidity and airflow speed were controlled by the heat-valve, spray-valve, eliminating-damp-valve and the wind-machine, respectively. The wind speed was not considered in this paper because the machine ran in full career all long. In this way, wood moisture content can be controlled by regulating the temperature and the humidity in the kiln. The measuring equipments had two temperature sensors, two humidity sensors and six moisture content sensors, and these were used to gather the experimental data at the normal running state of the kiln.
3.1 Experiment and results of Fraxinus mandshuricaThe first experimental species was Fraxinus mandshurica. 397 pairs of data of moisture content from 30% to 15% were used as training swatches. Training was made according to the neural network structure and algorithm mentioned. The parameters of the network are chosen as follows:the number of hidden layer nodes was 15, the studying ratio was 0.8, the activate function of hidden layer unit and output unit was Sigmoid function, the initial weights were chosen randomly in (0, 1), the final error E was 0.01. After training 39 629 times, the network converged and gained the weight value matrix (the matrix of input layer- hidden layer was 8×15, the matrix of hidden layer-output layer was 15×1), namely the drying schedule model was obtained after that. 1 108 pairs of data of moisture content from 30% to 8% were predicted by the prediction model. Using the data of temperature and humidity measured as inputs, we got the output of the network, i.e., wood moisture content. The predicted output of network (1) and the actual output of system (2) are shown as Fig. 3. The error between network output and actual output is shown as Fig. 4. The results showed that the network output was very close to the actual output except for several swatches. With the help of these data, we concluded that the neural network model established could approach the actual system well, had a very good ability of extrapolating, and could predict the decline of the moisture content more accurately.
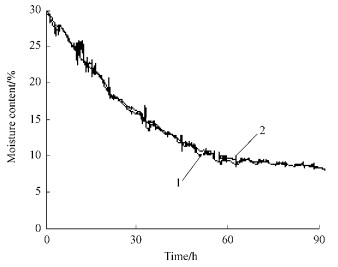
|
Fig.3 Drying curves of network and system outputs of Fraxinus mandshurica |

|
Fig.4 Error between network output and system output of Fraxinus mandshurica |
The second experiment was on Betula platyphylla. Training swatches were 71 pairs of data of moisture content from 30% to 20%. The parameters of the network were chosen as follows:the number of hidden layer nodes was 15, the studying ratio of network was 0.9, the activate function of hidden layer unit and output unit was sigmoid function, the initial weights were chosen randomly in (0, 1), the final error E was 0.02. Prediction swatches are 376 pairs of data of moisture content from 20% to 10%. The predicted output of network (1) and the actual output of system (2) are shown as Fig. 5. The error between network output and actual output is shown as Fig. 6.

|
Fig.5 Drying curves of network and system outputs of Betula platyphylla |
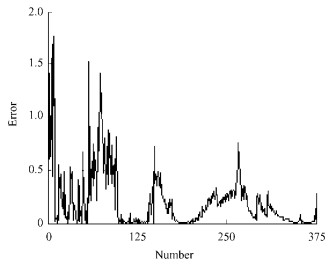
|
Fig.6 Error between network output and system output of Betula platyphylla |
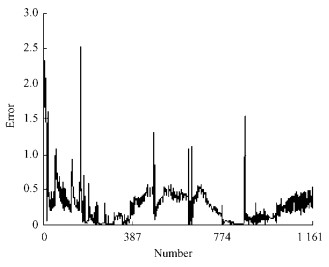
The third experiment was on Xylosma racemosum. Training swatches were 356 pairs of data of moisture content from 30% to 20%. The parameters of the network were chosen as follows:the number of hidden layer nodes was 15, the studying rate of network was 0.9, the activate function of hidden layer unit and output unit was sigmoid function, the initial weights were chosen randomly in (0, 1), the final error E was 0.01. Prediction swatches were 1 161 pairs of data of the same kiln whose moisture content was from 20% to 7%. The predicted output of network (1) and the actual output of system (2) are shown as Fig. 7. The error between network output and actual output is shown as Fig. 8.
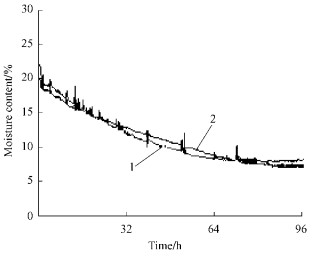
|
Fig.7 Drying curves of network and system outputs of Xylosma racemosum |
|
Fig.8 Error between network output and system output of Xylosma racemosum |
In this paper, the model of moisture content schedule was established to predict moisture content of wood drying based on time-delay neural network. It was trained and tested by experimental drying data of three species (Fraxinus mandshurica, Betula platyphylla and Xylosma racemosum). The results showed that there were several jumping data because of strong coupling of humidity and temperature in wood drying process, which brought biggish error in predicted results of some swatches. But most of the results were very close to actual value, which were proved that the network model could predict changing characteristic of moisture content very well in the practical process. The mathematical modeling of drying schedule offered the rules for operating and controlling drying equipment more effectively, which was of importance for industry.
Carlsson P, Arfvidsson J. 2000. Optimized wood drying. Drying Technology, 18(8): 1779-1796. DOI:10.1080/07373930008917810 |
Cronin K, Baucour P, Abodayeh K, et al. 2003. Probabilistic analysis of timber drying schedules. Drying Technology, 21(8): 1433-1456. DOI:10.1081/DRT-120024487 |
Fortin Y, Defo M, Nabhani M, et al. 2004. A simulation tool for the optimization of lumber drying schedules. Drying Technology, 22(5): 963-983. DOI:10.1081/DRT-120038575 |
Hukka A. 2000. Deformation properties of finnish spruce and pine wood in tangential and radial directions in association to high temperature drying. Part Ⅲ. Experimental results under drying conditions (mechano-sorptive creep). Holz als Roh-und Werkstoff, 58: 63-71. DOI:10.1007/s001070050389 |
Hu M Y. 1997. Study and application of mathematical model of wood drying schedule. Forestry Industry, 24(6): 4-6. |
Kaiser M. 1994. Time-delay neural networks for control. IFAC Symposium on Robot Control, Capri, Italy, 851-856.
|
Narendra K S, Parthsarathy K. 1990. Identification and control of dynamical systems using neural networks. IEEE Transactions on Neural Networks, 1(1): 4-27. DOI:10.1109/72.80202 |
Palancar M C, Aragon J M, Castellanos J A. 2001. Neural network model for fluidised bed dryers. Drying Technology, 19(6): 1023-1044. DOI:10.1081/DRT-100104803 |
Shi D, Zhang H J, Yang L M. 2002. Time-delay neural network for the prediction of carbonation tower's temperature. 19th IEEE Instrumentation and Measurement Technology Conference, Anchorage, Alaska, USA, 379-383. https://ieeexplore.ieee.org/document/1232356
|
Sun Z F, Bannister P, Carrington C G. 2000. Dynamic modeling of the wood stack in a wood drying kiln. Chemical Engineering Research & Design, 78(A1): 107-117. |
Wang Kejun(王科俊), Wang Kecheng(王克成). 1996. Neural network for modeling, prediction and control. Harbin: Harbin Engineering University Press(哈尔滨: 哈尔滨工业大学出版社), 10-16.
|
Wu Tao(吴涛), Liu Dengying(刘登瀛), Xu Xiaoming(徐晓鸣), et al. 2001. Using neural network to extrapolate and predict precipitation rate in drying course. Journal of Shanghai Jiaotong University(上海交通大学学报), 33(5): 596-599.
|
Xu Lina(徐丽娜). 1999. Neural network for control. Harbin: Harbin Industry University Press(哈尔滨: 哈尔滨工业大学出版社), 45-48.
|
 2008, Vol. 44
2008, Vol. 44
