文章信息
- 葛宏立, 周国模, 刘恩斌, 刘安兴, 叶耿平.
- Ge Hongli, Zhou Guomo, Liu Enbin, Liu Anxing, Ye Gengping
- 浙江省毛竹直径与年龄的二元Weibull分布模型
- Diameter-Age Bivariate Weibull Distribution Model for Moso Bamboo Forests in Zhejiang Province
- 林业科学, 2008, 44(12): 15-20.
- Scientia Silvae Sinicae, 2008, 44(12): 15-20.
-
文章历史
- 收稿日期:2007-08-09
-
作者相关文章
2. 浙江省森林资源监测中心 杭州 310020
2. Monitoring Center for Forest Resources in Zhejiang Province Hangzhou 310020
中国的毛竹林面积约400万hm2,竹产量占到世界的1/2以上。毛竹(Phyllostachys edulis)是重要的森林碳库,固碳能力相当强大,对气候变化具有不可低估的影响(周国模等,2004),并且还是山区农民经济收入的重要来源。目前有关毛竹林的研究主要有栽培管理(吴家森等,2005;舒常庆等,1999;洪伟等,1998b)、生物量及碳(洪伟等,1998a;陈辉等,1998;何东进等,2003;周国模等,2004)和林分结构(郑郁善等,1998;张贵等,2002;尤添革等,2004;周国模等,2006),有关毛竹林胸径和年龄结构的研究相对较少(戚连忠等,2000;罗明灿等,2001;张贵等,2002)。
研究毛竹林分尺度上的胸径、年龄结构有助于科学、合理地经营以及进行林分尺度的生态状况研究。研究宏观尺度上的直径、年龄结构,有助于从宏观上了解毛竹资源的现状及消长情况,为宏观决策提供依据。研究这些结构特征通常需要应用概率分布模型,林业上常用的有Weibull分布模型等。Weibull分布模型一般分为一元和二元2类。一元Weibull分布模型在林业上的应用已有一定历史(Bailey et al., 1973;寇文正,1982;孟宪宇, 1985;Shiver,1988;Kilkki et al., 1989;Khatouri et al., 1990;周国模,1992;De Groot et al., 1994;Maltamo, 1995, 1997;Bondarev,1996;Baldwin et al., 1997;刘君然等,1997;吴承祯等,1998;Nanos et al., 2000;Till et al., 2003;亢新刚等,2003;杨锦昌等,2003;王韩民等,2005;Zhang et al., 2006;王顺忠等,2006;董文宇等,2006)。这些研究用直径、年龄、树叶重量、松脂产量和松球果生存等单个因子描述林分某个方面的结构。一元Weibull分布模型只能描述一维结构,而一个林分中的结构有时候需要从二维方面来描述,如直径与树高,直径与年龄等。林业上对二元分布模型的研究和应用相对较少,但还是有一些,如:用二维分布模型SBB来描述林分直径与树高二维结构,SBB的两个边际分布是SB分布(Schreuder et al., 1977);用二元Weibull分布函数描述天然更新幼树数量与林分平均直径和树高的二维关系(Schweiger et al., 1997);用二元Weibull分布函数和二元Beta分布函数来描述树冠内细枝叶面积分布的二维结构(Temesgen et al., 2003)。
竹子是典型的异龄林结构,同时描述直径与年龄能更完整地反映竹林资源的结构特征。笔者仅见过1例用二元Weibull模型描述直径与年龄二维结构的研究:描述毛竹株数随直径、年龄的分布结构(周国模等,2006),但该研究中的模型是否满足一般概率模型的要求值得商榷,如不能证明概率密度非负,不能证明其边际分布就是一元Weibull分布等。笔者认为Larry Lee等人介绍的二元Weibull分布模型是满足二元概率分布模型要求的(Marshall et al. 1967;Larry Lee,1979;Lu et al. 1990;姜美辰等,2005;史道济等,2003)。本研究探讨用满足概率模型基本特征的二元Weibull分布模型描述毛竹林的直径与年龄二维结构。
1 研究区概况浙江省位于我国东南沿海,是我国毛竹分布最丰富的省份之一,有“世界毛竹看中国,中国毛竹看浙江”之说。据2004年调查数据,全省有森林面积584万hm2,其中毛竹林65万hm2。浙江省地处中亚热带,全省年平均气温15~18 ℃,年平均降水量1 000~2 000 mm,1, 7月分别为全年气温最低和最高的月份,5, 6月为集中降雨期。毛竹林立竹密度2 500~4 500株·hm-2,生物量干质量80~100 t·hm-2。
2 数据来源浙江省于1979年建立了作为国家森林资源连续清查体系组成部分的省级森林资源清查体系,共设置固定样地4 250个,以5年为1个复查周期,到2004年已经调查了6次(分别为1979,1986,1989,1994,1999与2004年)。抽样方式为系统抽样,样点格网为4 km×6 km,样地形状为正方形,边长28.28 m,面积800 m2。
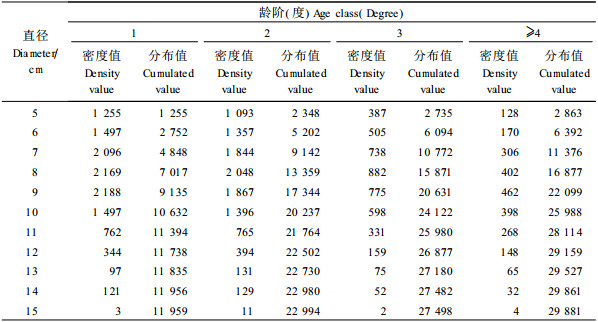
本研究利用到目前为止最新的浙江省森林资源连续清查数据即2004年的调查数据,选择4 250个固定样地中的毛竹纯林样地共245个。样地内5 cm以上的竹子均调查记载直径(胸径)和龄阶,其中直径以1 cm为径阶记载,龄阶以“度”记载,1年生竹记为1度竹,2~3年生竹记为2度竹,4~5年生竹记为3度竹,4度为6~7年生竹,依此类推。将245个样地的数据合并统计到表 1(该表中的数据与周国模等(2006)的数据略有差异,原因是本文增加了几个样地),本文以后出现的株数单位均是245个样地面积上的株数。每个样地毛竹株数为18~461株,平均122株,总共29 881株。表中密度值为某个径阶、龄阶的毛竹株数,分布值为从起始径阶、起始龄阶到某个径阶、龄阶的毛竹株数的累积值。
|
|
1979年,Larry Lee提出了一类二元Weibull分布,其生存函数为(Larry,1979;史道济等,2003;姜美辰等,2005)
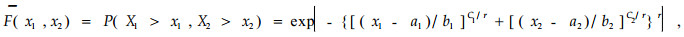
|
(1) |
式中:X1与X2表示2个随机变量,X1与X2分别为它们的取值;a1,a2为位置参数;b1, b2为尺度参数;c1, c2为形状参数,X1>a1, X2>a2。在区域X1≤a1,X2≤a2内,概率密度定义为0。b1,b2>0,c1,c2>0,1≥r>0; Hougaard(1986)指出,生存函数(1)是一个很有价值的模型。实际上它描述了一种成对相关寿命时间的模型。当r趋向于1时表示X1,X2之间相互独立;当r趋向0时表示X1, X2之间存在某种确定性关系。将直径和年龄看成连续变量,则直径要达到一定大小时才会有毛竹出现,所以直径的位置参数应大于0,而年龄只要大于0,就会有毛竹出现,所以毛竹的位置参数可看成是0,本研究的实际计算也证实了这一点。用D和T分别表示随机变量直径和龄阶,用d和t分别表示它们的取值,则生存函数(1)可改写为
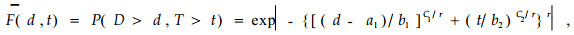
|
(2) |
式中:P(D>d, T>t)表示直径>d、年龄(度)>t时生存毛竹的概率。a1,b1,b2,c1,c2,r为模型的6个参数。若假设二元Weibull函数的概率密度函数为f(D, T),则
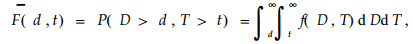
|
(3) |
即图 1中f(D, T)在阴影区域上的积分。假设S(D>d, T>t)表示D>d, T>t时生存毛竹的株数,则:

|
图 1 二元Weibull分布生存函数 Figure 1 Bivariate Weibull distribution survival function |
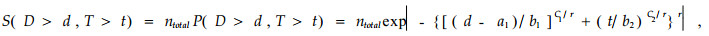
|
(4) |
式中:ntotal为总的毛竹株数,这里也作为参数估计。将生存函数(2)写成分布函数形式:
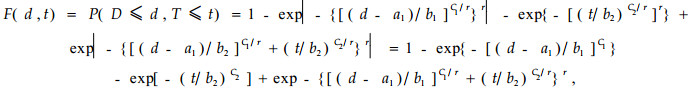
|
(5) |
它是图 2中f(D, T)在阴影区域上的积分。很显然,在(5)中令t→∞,就得到

|
图 2 二元Weibull分布函数 Figure 2 Bivariate Weibull distribution function |
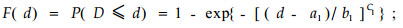
|
(6) |
若令d→∞,就得到
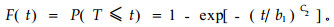
|
(7) |
可见,毛竹的二元Weibull分布模型的边际分布分别是直径和年龄的一元Weibull分布。另外,分析生存函数(2)可知,二元Weibull分布的生存函数是一个严格的降函数,因此对于分布函数(5)有:F(d, t)非减;F(+∞, +∞)=1。所以本文介绍的二元Weibull分布模型具有严格的概率模型性质。
记S(D≤d, T≤t)为D≤d, T≤t时毛竹的株数,则

|
(8) |
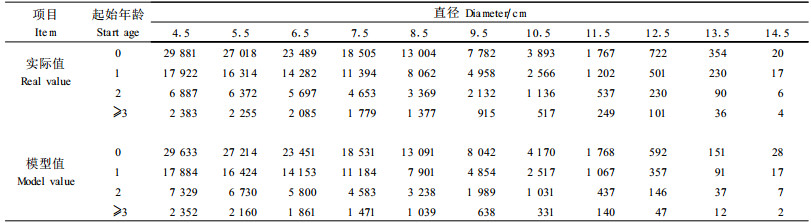
从理论上讲,根据公式(2)、(4)、(5)及(8)均可以估计参数,但本研究认为,用公式(4)估计较为简单、稳定。为了根据公式(4)估计参数,根据表 1数据整理出表 2中的实际值数据作为估计参数的原始数据:依据公式(4)的积分形式和图 1中阴影部分所示进行统计。表 2中起始年龄列的0表示1度竹的积分起点,1表示2度竹的积分起点,等等;直径的4.5表示5 cm径阶的积分起点,5.5表示6 cm径阶的积分起点,等等。这样表示的目的是为了数学处理的方便,是为了将离散变量(度和径阶均是离散的)作为连续变量处理。参数ntotal,a1,b1,c1,b2,c2和r的计算结果分别为32 024.0,0.556 860,8.154 830,3.655 868,1.535 296,1.422 527和0.914 141,R2=0.999。由于r = 0.914 141,接近于1,表示D,T之间接近独立,从模型的简单及稳定性出发,令r = 1,(4)和(8)相应改写为:
|
|
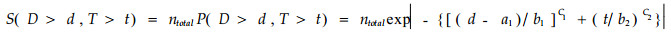
|
(9) |
和
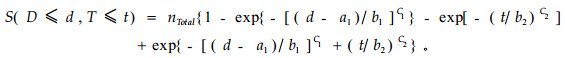
|
(10) |
用表 2的实际数据和公式(9)重新估计参数,得到ntotal,a1,b1,c1,b2和c2分别为31 483.0, 0.919 248, 7.863 786, 3.564 237, 1.592 615和1.468 143,R2=0.999。模型值见表 2,可见模型的拟合结果是非常令人满意的。
5 各径阶和各度毛竹的模型株树(即模型密度值)假设P(d,t)表示落在龄阶为t,径阶为d的毛竹的株数概率。如图 3所示,对阴影部分进行积分,其值就是落在阴影部分的毛竹株数概率。方便起见,作如下简化约定:
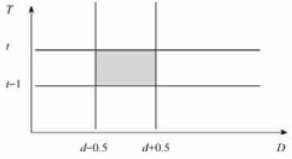
|
图 3 各径阶和各龄阶的毛竹分布区域 Figure 3 Distribution area by diameter class and age class |
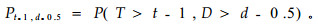
|
其他类推。
显然,当1≤T≤3时,有
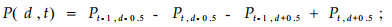
|
(11) |
当T=4时,

|
(12) |
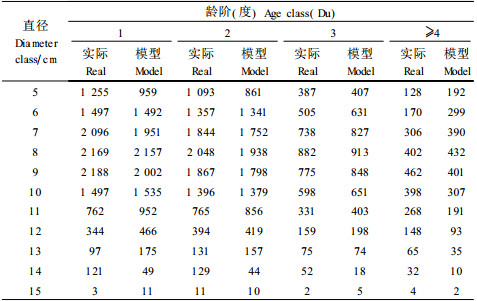
P(d, t)乘以nTotal就得到相应的毛竹株数的估计值。也可以在(11)和(12)中直接考虑株数。计算结果见表 3。模型值合计为29 631株,比表 2中的模型值29 633株略少,这是因为表 2中的数值是d→∞, t→∞时的数据,而表 3实际上不是(因为实际计算时d和t不可能真正趋向无穷),但二者相差非常小,表明表 3区域外的数据可忽略不计。比较各单元格的实际值与模型值,都很接近,可见用二元Weibull模型描述毛竹株数随直径、年龄的变化规律是可行的。
|
|
本文分别建立了直径一元Weibull模型(6)式、年龄一元Weibull模型(7)式、带相关参数r的二元Weibull模型(4式)与不带相关参数r的二元Weibull模型(9式),现对通过不同模型估计的参数进行比较(表 4)。
|
|
从表 4可看出,2个二元Weibull模型的参数中,除了位置参数a1相差较大外,其余都很接近,说明可以认为直径和年龄两个变量是独立的。而一元Weibull模型的参数与二元Weibull模型的参数除了a11之外,也很接近。这说明:毛竹二元Weibull模型的2个边际分布不仅在理论上是直径和年龄的一元Weibull模型,且在实际计算的参数数值上也很接近;用Weibull模型描述毛竹分布是合适的,且模型具有稳定性。
7 结论与讨论过去林业上应用的Weibull分布基本是一元的,即只描述直径。直径结构固然重要,但对异龄林来说,年龄结构也很重要,尤其对于以发挥生态功能为主的森林来说。直径结构与年龄结构一起描述,比单纯描述其中一个结构更有意义。本例说明,毛竹直径的分布接近正态分布,年龄的分布则介于指数分布和χ2分布之间。Weibull分布的适应性很好,能描述常见的几种分布,这种性质很适合在林业上应用。本研究提出的方法对于研究毛竹林二维结构具有重要的意义,对于研究其他树木型的森林资源的二维结构也有积极的参考价值。
本文介绍的二元Weibull分布模型具有严格的概率模型性质,如:分布函数非减,密度函数非负,分布函数的极限为1,2个边际分布均是一元Weibull分布等。一元Weibull分布不仅在理论和形式上是二元Weibull分布的边际分布,而且用边际分布求得的参数与用联合分布求得的参数也很接近。
本文实例是省级宏观模型,它描述的是一个宏观区域的毛竹二维结构情况,可用于宏观分析和宏观决策。但本文的方法从理论上讲是可以应用到林分水平上来的,以指导毛竹林的的经营管理,但实际情况如何,还需要继续研究。
概率模型的参数估计有多种方法,如最大似然法、最小二乘法等,本文采用的是最小二乘法。用于估计参数的模型表达式也可以是分布函数、概率密度函数、生存函数,本文采用的是分布函数(一元)和生存函数(二元),而且作为因变量的是实际株数,而不是概率。用其他估计方法、其他模型表达式、其他因变量估计参数会带来哪些变化,本文均没有进行探讨,留待以后研究。
陈辉, 洪伟, 兰斌, 等. 1998. 闽北毛竹生物量与生产力的研究. 林业科学, 34(1): 60-64. |
董文宇, 邢志远, 惠淑荣, 等. 2006. 利用Weibull分布描述日本落叶松的直径结构. 沈阳农业大学学报, 37(2): 225-228. DOI:10.3969/j.issn.1000-1700.2006.02.023 |
何东进, 洪伟. 2003. 武夷山毛竹天然林生物量与能量分配规律及其与人工林的比较研究. 西北植物学报, 23(2): 291-296. DOI:10.3321/j.issn:1000-4025.2003.02.017 |
洪伟, 郑郁善, 陈礼光. 1998a. 毛竹枝叶生物量模型研究. 林业科学, 34(Sp.1): 11-15. |
洪伟, 郑郁善, 邱尔发. 1998b. 毛竹丰产林密度效应研究. 林业科学, 34(Sp.1): 1-4. |
姜美辰, 叶慈南, 徐冬元. 2005. 一类二元相关威布尔分布及其参数估计. 系统科学与数学, 25(6): 711-719. DOI:10.3969/j.issn.1000-0577.2005.06.009 |
亢新刚, 胡文力, 董景林, 等. 2003. 过伐林区检查法经营针阔混交林林分结构动态. 北京林业大学学报, 25(6): 1-5. DOI:10.3321/j.issn:1000-1522.2003.06.001 |
寇文正. 1982. 林木直径分布的研究. 南京林产工业学院学报, (2): 51-65. |
刘君然, 赵东方. 1997. 落叶松人工林威布尔分布参数与林分因子模型的研究. 林业科学, 33(5): 412-417. |
罗明灿, 刘惠民, 韩灯, 等. 2001. 龙竹林分结构的初步研究. 竹子研究汇刊, 20(1): 15-18. DOI:10.3969/j.issn.1000-6567.2001.01.004 |
孟宪宇. 1985. 使用Weibull分布对人工油松林直径分布的研究. 北京林学院学报, 7(1): 30-39. |
戚连忠, 朱杭瑞, 蔡琳, 等. 2000. 从文献分析看浙江省竹类研究进展. 浙江林业科技, 20(6): 68-72. DOI:10.3969/j.issn.1001-3776.2000.06.017 |
史道济, 唐爱丽, 汪玲. 2003. 二元威布尔分布形状参数相等的检验. 天津大学学报, 36(1): 68-71. |
舒常庆, 曹流清. 1999. 湖南省会同县肖家乡毛竹数量化地位指数表的研究. 华中农业大学学报, 18(1): 92-95. DOI:10.3321/j.issn:1000-2421.1999.01.025 |
王韩民, 惠刚盈. 2005. 林木最近距离分布模型的研究. 林业科学研究, 18(5): 556-560. DOI:10.3321/j.issn:1001-1498.2005.05.010 |
王顺忠, 王飞, 张恒明, 等. 2006. 长白山阔叶红松林径级模拟研究——林分模拟. 北京林业大学学报, 28(5): 22-27. DOI:10.3321/j.issn:1000-1522.2006.05.005 |
吴承祯, 洪伟. 1998. 杉木人工林胸径的Weibull分布及其最优拟和研究. 江西农业大学学报, 20(1): 86-90. |
吴家森, 周国模, 徐秋芳, 等. 2005. 不同年份毛竹营养元素的空间分布及与土壤养分的关系. 林业科学, 41(3): 171-173. DOI:10.3321/j.issn:1001-7488.2005.03.028 |
杨锦昌, 江希钿, 许煌灿, 等. 2003. 马尾松人工林直径分布收获模型及其应用研究. 林业科学研究, 16(5): 581-587. DOI:10.3321/j.issn:1001-1498.2003.05.010 |
尤添革, 林秀琴. 2004. 毛竹林的连续型直径分布变化方程. 生物数学学报, 19(4): 453-456. DOI:10.3969/j.issn.1001-9626.2004.04.011 |
张贵, 陈建华. 2002. 应用Weibull分布研究毛竹林分直径结构规律. 经济林研究, 20(4): 31-33. DOI:10.3969/j.issn.1003-8981.2002.04.008 |
郑郁善, 洪伟. 1998. 毛竹林丰产年龄结构模型与应用研究. 林业科学, 34(3): 32-38. DOI:10.3321/j.issn:1001-7488.1998.03.005 |
周国模, 姜培坤. 2004. 毛竹林的碳密度和碳贮量及其空间分布. 林业科学, 40(6): 20-24. DOI:10.3321/j.issn:1001-7488.2004.06.004 |
周国模, 刘恩斌, 刘安兴, 等. 2006. Weibull分布参数辨识改进及对浙江毛竹林胸径年龄分布的测度. 生态学报, 26(9): 2919-2924. |
周国模. 1992. 杉木人工林直径分布的研究. 福建林学院学报, 12(4): 399-405. |
Bailey R L, Dell T R. 1973. Quantifying diameter distributions with the Weibull function. Forest Science, 19: 97-104. |
Baldwin V C J, Peterson K D, Burkhart H E, et al. 1997. Equations for estimating Loblolly pine branch and foliage weight and surface area distributions. Canadian Journal of Forest Research, 27: 918-927. DOI:10.1139/x97-030 |
Bondarev A. 1996. Age distribution patterns in open boreal Dahurican larch forests of Central Siberia. Forest Ecology and Management, 93: 205-214. |
De Groot P, Fleming R A. 1994. Analysis and modelling of cohort life tables of Jack pine seed cones. Canadian Journal of Forest Research, 24: 1579-1592. DOI:10.1139/x94-206 |
Hougaard P. 1986. A class of multivariate failure time distribution. Biometrika, 73(3): 671-678. |
Khatouri M, Dennis B. 1990. Growth-and-yield model for uneven-aged Cedrus atlantica stands in Morocco. Forest Ecology and Management, 36: 253-266. DOI:10.1016/0378-1127(90)90029-B |
Kilkki P, Maltamo M, Mykkänen R, et al. 1989. Use of the Weibull function in estimating the basal area dbh-distribution. Silva Fennica, 23(4): 311-318. |
Larry Lee. 1979. Multivariate distribution having Weilbull properties. Journal of Multivariate Analysis, 9: 267-277. DOI:10.1016/0047-259X(79)90084-8 |
Lu J C, Bhattacharyya G K. 1990. Some new constructions of bivariate Weibull models. Annals of the Institue of Statistical Mathematics, 42: 543-559. DOI:10.1007/BF00049307 |
Maltamo M, Puumalainen J, Päivinen R. 1995. Comparison of beta and Weibull functions for modelling basal area diameter distributions in stands of Pinus sylvestris and Picea abies. Scandinavian Journal of Forest Research, 10: 284-295. DOI:10.1080/02827589509382895 |
Maltamo M. 1997. Comparing basal area diameter distributions estimated by tree species and for the entire growing stock in a mixed stand. Silva Fennica, 31: 53-65. |
Marshall A W, Olkin I. 1967. A multivariate exponential distribution. Journal of the American Statistical Association, 62: 30-44. DOI:10.1080/01621459.1967.10482885 |
Nanos N, Tadesse W, Montero G, et al. 2000. Modelling resin production distributions for Pinus Pinaster ait using two probability functions. Annals of Forest Science, 57: 369-377. |
Schreuder H T, Hafley W L. 1977. A useful bivariate distribution for describing stand structure of tree heights and diameters. Biometrics, 33(3): 471-478. DOI:10.2307/2529361 |
Schweiger J, Sterba H. 1997. A model describing natural regeneration recruitment of Norwayspruce in Austria. Forest Ecology and Management, 97: 107-118. DOI:10.1016/S0378-1127(97)00092-3 |
Shiver B D. 1988. Sample sizes and estimation methods for the Weibull distribution for unthinned Slash pine plantation diameter distributions. Forest Science, 34: 809-814. |
Temesgen H, Valerie M LeMay, Cameron Ian R. 2003. Bivariate distribution functions for predicting twig leaf area within hybrid spruce crowns. Canadian Journal of Forest Research, 33: 2044-2051. DOI:10.1139/x03-127 |
Till N, Luciano V D, Joao R-d S, et al. 2003. Tropical forest stand table modelling from SAR data. Forest Ecology and Management, 186: 159-170. DOI:10.1016/S0378-1127(03)00234-2 |
Zhang L, Liu C. 2006. Fitting irregular diameter distributions of forest stands by Weibull, modified Weibull, and mixture Weibull models. Journal of Forest Research, 11: 369-372. DOI:10.1007/s10310-006-0218-7 |
 2008, Vol. 44
2008, Vol. 44