按照传统，通常采用无疵小试样测试来确定结构用锯材的力学性质，即选择完全没有腐朽、节子、斜纹理、压缩破坏、脆心、轮裂、开裂、钝棱、钻孔等缺陷的试样进行测试。考虑到树木生长过程中形成的各种缺陷可能会对结构用锯材力学性质产生影响，在确定最终设计值时，往往会采用保守的假设条件，进行适当的折减，从而严重影响了设计精度。

具体说来，在各种缺陷中, 以节子和纹理方向的变化对结构用锯材力学性质的影响最为明显。通常节子在生长的树木内部几乎不产生结构性的降等；然而，一旦原木被锯解，节子周围分布着的相互联系的纤维的复杂形式就被破坏，纤维结构失去连续性，收缩量产生差别，强度值降低(Madsen, 1992)。节子对结构用锯材的力学性质影响程度依次为：顺纹拉伸强度(UTS)、弯曲强度(MOR)、顺纹压缩强度(UCS)、弯曲弹性模量(MOE)。节子的出现改变了宽面MOE和窄面MOE的比值，并且随着节子尺寸增加，MOR和MOE均减少。就节子类型而言，含有边节的板材的拉伸强度要明显低于含有中线节的板材(Phillips et al., 1981; Kunesh et al., 1972；Grant et al., 1984；Nguedjio, 1999)。斜纹理对结构用锯材强度性质的影响仅次于节子。按照Hankinson公式，在对无疵小试样进行拉伸时，纹理角度每倾斜5°，强度损失超过20%以上。除此以外，锯材尺寸和锯解方式也会影响到结构用锯材的力学性质。一般说来，随着锯材长度增加，内部的材料缺陷增加，密度变异程度加大，拉伸强度降低。此外，根据经典的脆性断裂理论，锯材宽度也会对结构用锯材的力学性质产生直接影响。

目前，世界上各个国家正在尝试利用足尺测试来代替传统的无疵小试样测试，其目的在于使测试得到的力学性能可以满足实际使用载荷条件和气候条件。一些国家已经建立了相应的测试标准，但是，不同国家标准的具体测试方法各不相同。

规格材作为一种结构用锯材，被广泛地应用在现代轻型木结构当中，因此，为了做到材料的合理高效利用，建筑者和使用者越来越关注规格材的力学性质评估问题。目前国际上一致认可通过分级测试方法来评估结构用规格材的力学性质。

本研究引进先进的足尺强度测试设备，遵循分级测试的理念，依照我国的GB/T 50329进行弯曲测试(中华人民共和国建设部等, 2003)，依照北美的ASTM D 4761进行压缩测试(ASTM，2004)，通过3项主要强度指标：静态弯曲强度(MOR)、静态弯曲弹性模量(MOE)、顺纹压缩强度(UCS)来评估规格材的结构性质，为下一步修订完善我国的规格材强度性质测试标准提供依据。

我国目前结构用锯材主要以人工林为主，其中，最重要的人工林树种包括杉木(Cunninghamia lanceolata)、马尾松(Pinus massoniana)、杨树(Populus)，面积依次为921.5、583.27、413.63 hm²(雷加富, 2005)。其中以杉木人工林蓄积量最大。杉木分布于我国17个省，北至秦岭，南至广东，东到浙江、台湾，西到云南和四川，分布面积广泛，并且在2003年《中国木结构设计规范》中将人工林杉木列为一种结构用材树种。因此，本研究中采用人工林杉木为试材。

1 材料与方法 1.1 试验材料

从杉木人工林的3个主产区——安徽、湖南、四川采集试材。按照每一地区杉木人工林蓄积量的比例，选择胸径在25~32 cm之间的立木，树龄在35年左右，共计48株进行测试。试样应该代表树种种群、地形、气候、生长方式的分布情况。原则上要求对于每个产地、每个尺寸、每个等级至少选择20个试样进行测试。

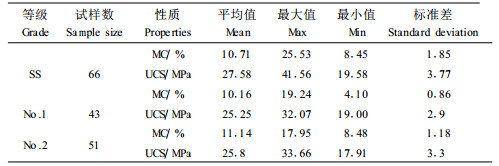
在确保最大出材率的前提下，将原木锯解成板材，干燥至含水率约为20%，刨光后得到尺寸为45 mm×90 mm×2 600 mm的规格材(注：北美的2″×4″规格材尺寸为38 mm×89 mm，本试验由于采用了人工林，因此依据相关规定将尺寸进行了适当放大)。然后，将试样放置在调温调湿间内进行平衡含水率处理，并且定期随机抽样检测含水率，确保试样达到当地的平衡含水率。按照北美锯材目测分等规则NLGA，根据规格材的天然缺陷、干燥缺陷、加工时造成的人为缺陷，将规格材划分为SS、No.1、No.2 3个等级(注：北美将规格材目测分等为SS、No.1、No.2、No.3、Economy 5个等级，因为后2个等级的实际利用价值不大，因此，本文只考虑前3个等级)。杉木取样株数和板材数量，见表 1。

1.2 测试方法

本研究中，依照GB/T 50329进行弯曲测试，跨高比为18:1，三分点加荷，边弯，留有充分的外悬量以防止测试过程中试样从支座处滑脱，确保测试过程的稳定性。拉伸边任意选择。在选择测试区域时，将最大降等缺陷放置在跨度范围内。应该尽量避免把钝棱、大面积腐朽等缺陷放置在加荷位置，避免由于大面积木材面积缺失或者局部丧失承载能力而出现测量误差。在全跨度范围内采用U型设备来测量在跨中位置试样的中性轴相对于端部支座的位移，作为弯曲变形量。此U型设备与数据采集设备连接，将变形量数据输出到计算机，与载荷数据进行同步实时处理，绘制出载荷-变形曲线，取线弹性部分通过计算得到表观弹性模量。然后，取下U型设备，重新进行弯曲测试，施加载荷直至试样发生破坏，根据峰值载荷和试样尺寸计算得到弯曲强度。

依照ASTM D4761进行顺纹压缩测试。由于试件几何条件的限制，本试验采用短柱压缩测试。美国林产品实验室的Green等(1988)研究表明，长柱和短柱的压缩强度平均值的差异约为20%，以短柱测试结果为高，在进行设计值计算时应当考虑这一点。首先，从每1个试件中截取1个包含主要降等缺陷的试件和1个包含次要降等缺陷的试件，长度均为350 mm，分别代表顺纹压缩强度最薄弱的2个截面，注意锯解时锯口不经过主要缺陷。然后对于上述2个试样分别施加轴向压缩载荷。为了使载荷均匀地分布在接触表面上，而不产生偏心，采用一个圆球形的支撑块，其最小半径应该便于调整支承板，最大半径应当可以提供足够大的接触面积，此半径一般为试样的最大横截尺寸的1~2倍。支撑块的球心应当落在试样的接触平面上，根据球转动的中心来调整试样在支撑板上的移动，以确保轴向加载。逐渐施加轴向压缩载荷，直至发生破坏。取2个短柱试件最终载荷的最小值作为顺纹压缩最终破坏载荷。此外，为了防止试件在压缩测试过程中发生扭曲，采用非连续的侧向支撑，允许试件在加荷方向运动，且摩擦阻力最小，侧向支撑之间的距离不超过横截面回转半径的17倍。根据顺纹压缩最终载荷和横截面尺寸来计算顺纹压缩强度。

在试样发生破坏之后，立即从每个试样中尽可能靠近破坏处的位置，截取含水率小试样，以更加完整描述试样的基本物理性质。

2 结果

就各个目测等级的试样数而言，SS＞No.2＞No.1。主要的降等缺陷包括节子、钝棱、斜纹理、劈裂、腐朽。

45 mm×90 mm×2 600 mm规格材的弯曲测试结果见表 2。可见SS等级的MOE平均值比No.1等级高4.6%，比No.2等级高1.4%。No.1等级的MOE平均值低于No.2等级。这与Barrett等(1994)的研究结果相似。而MOR平均值也表现相似趋势：SS＞No.2＞No.1。

45 mm × 90 mm×2 600 mm规格材的顺纹压缩测试结果见表 3。可见UCS平均值也表现相似趋势：SS＞No.2＞No.1。

利用非参数方法来确定MOE、MOR、UCS的5%分位值。经过尺寸调整和含水率调整之后，得到弯曲弹性模量(MOE)特征值别是10.34、9.87和10.17 GPa。弯曲强度(MOR)特征值分别是26.93、20.25和20.74 MPa。顺纹压缩强度(UCS)特征值分别是21.59、20.64和20.33 MPa。

在进行以可靠性为基础的设计时，通常运用锯材性质之间的关系，来预测未经过测试的树种的某些性质、指导建立强度等级系统、支持发展无损检测分级系统。因此有必要以弯曲强度为基础，采用百分点数据来对比研究性质之间关系，UCS与MOR之间的关系见图 1、2和3。结果表明，随着弯曲强度增加，UCS/MOR降低，这与以前无疵小试样结论一致。足尺测试和无疵小试样测试结果仅仅在UCS/MOR水平方面存在某些差异，这可能是由于取样方法和测试方法不同造成的。本文获得的UCS与MOR之间的关系与美国树种研究结果(Green et al., 1991)和欧洲树种研究结果(Curry et al., 1977)趋势相同。

杉木人工林的无疵小试样数据表明，弯曲MOE、MOR的平均值分别是9.53 GPa和60 MPa。压缩强度的平均值是34.0 MPa(Luo et al., 1995)。表 2、3表明, SS等级、No.1等级、No.2等级规格材的弯曲弹性模量平均值分别是无疵小试样的1.13、1.08和1.12倍。弯曲强度平均值分别是无疵小试样弯曲MOR的84.8%、70.8%、78.7%，顺纹压缩强度平均值分别是无疵小试样的81.1%、74.3%、75.9%。

3 讨论

本研究中存在2个问题。第一，SS等级、No.1等级、No.2等级规格材的弯曲弹性模量平均值均高于无疵小试样。其原因可能在于：1)虽然在2种测试前均要求将试样调整到平衡含水率，但是规格材试样横截面含水率梯度较大，且沿着长度方向含水率不均匀。2)试样尺寸和横截面形状不同，小试样尺寸为300 mm×20 mm×20 mm，足尺试样尺寸为45 mm × 90 mm×2 600 mm，截面惯性矩不同。3)鉴于人工林特殊材性，研究中对规格材尺寸进行了适当的放大。第二，规格材目测等级和强度、刚度性质之间缺乏一致性，即通常认为目测等级高，则MOR和MOE高；但实际上2个相邻等级可能出现一定程度的重叠。其原因可能在于：1)前人对于黑云杉(Picea mariana)人工林规格材的研究已经表明，目测等级高并不意味着强度或者刚度就一定高。这是因为黑云杉人工林目测分等时，70%的降等是由于钝棱引起的，而钝棱属于表观缺陷，而非实质降低强度缺陷，且使用的目测分等规则对于节子是比较有效的。而本试验中的杉木人工林也可能存在相似问题。2)其他木材特征，例如：密度、幼龄材含量、生长速度等对于强度和刚度均有一定影响，而这些因素在目测分等过程中常常难于考虑(Zhang，2002；Bier，1986；Barrett et al., 1991)。3)本试验中还发现位于拉伸边的节子会降低弯曲强度，位于压缩边的节子会通过发生压缩破坏的形式释放掉传递过来的部分载荷，起到局部增强作用，导致在测试破坏载荷时出现2~4次峰值，表现为破坏的阶段性。因此，建议从上述几个方面对现行规格材目测分等规则中适当完善，以更好地把目测等级和主要强度性质对应起来。

4 结论

45 mm × 90 mm×2 600 mm规格材的弯曲弹性模量(MOE)、弯曲强度(MOR)、顺纹压缩强度(UCS)平均值均表现出相似趋势：SS＞No.2＞No.1。SS等级、No.1等级和No.2等级规格材的MOE特征值别是10.34、9.87和10.17GPa，MOR特征值分别是26.93、20.25和20.74 MPa，UCS特征值分别是21.59、20.64和20.33 MPa。

通过研究弯曲-压缩性质之间的关系发现，随着MOR增加，UCS/MOR降低。

将足尺测试结果与无疵小试样测试结果进行比较，发现足尺规格材的SS等级、No.1等级、No.2等级的MOE平均值分别是无疵小试样的1.13、1.08和1.12倍，MOR平均值分别是无疵小试样的84.8%、70.8%和78.7%，UCS度平均值分别是无疵小试样的81.1%、74.3%和75.9%。