真善美是人类共同追求的人生目标和科学理想。为弘扬和传承俄罗斯数学家李雅普诺夫(1857—1918年,图 1)的科学思想,俄罗斯国家邮政局于1957年在其诞辰100周年之际发行纪念邮票1枚(图 2)。从外表和气质来看,李雅普诺夫是典型的美男子,其温文尔雅、风度翩翩、谈吐非凡。然其追求科学和人生真善美的美丽心灵更是令人高山仰止、叹为观止。他是圣彼得堡数学学派的中流砥柱,为该学派的发展和繁荣做出了卓越贡献;他是凝炼和铸造大学灵魂的领军人物,所任教圣彼得堡大学、哈尔科夫大学深受其科学思想影响;他是俄罗斯著名天文学家和数学家,为俄罗斯跻身世界科技强国奠定了科学理论基础。
 |
图 1 李雅普诺夫 |
 |
图 2 李雅普诺夫纪念邮票 |
爱情是人类精神的最高唯美境界,是灵魂深处闪烁的光芒,其旷达放远且璀璨耀眼。由于笛卡儿(1596—1650年)、牛顿(1642—1727年)、莱布尼茨(1646—1716年)、切比雪夫(1821—1894年)、魏尔斯特拉斯(1815—1897年)等多位数学家终身未婚,致使世人误解数学家都是一群冷血动物。且不说阿贝尔(1802—1829年)死在未婚妻怀抱、伽罗瓦(1811—1832年)为爱情决斗、沃尔夫斯凯尔(?—1908年)为爱情欲走绝路,单表李雅普诺夫为爱情而自杀身亡的故事就令人唏嘘和感叹,有助于我们从另一个侧面认识数学家的浪漫情感生活。
李雅普诺夫为家中兄弟3人中的老大,其父曾在喀山大学天文台工作。然而父亲的英年早逝,彻底打碎了李雅普诺夫的美好憧憬。为减轻家庭负担,母亲只能允让姑妈把11岁的李雅普诺夫领去抚养,表妹娜塔莉娅从内心喜欢这个腼腆的表哥,他们一同成长、学习和玩耍。
俄罗斯当选科学院通讯院士的谢切诺夫(1829—1905年)是李雅普诺夫姑父之兄,常来其姑妈家做客。他创建了俄罗斯生理学派以及心理学自然科学流派。谢切诺夫常带来一些科普书籍,并给这对表兄妹讲科学家故事。故李雅普诺夫有幸阅读了不少俄、德和法文书籍,涵盖数学、天文、哲学、历史、民族志、政治经济学和文学等领域。
1870年,母亲领回了李雅普诺夫。虽与表妹难舍难分,但李雅普诺夫还是回到自己家中,从此开始了求学生涯。他要求直接插班到三年级学习,但仍感到很轻松,因不少科学知识已在姑妈家学过。1876年李雅普诺夫考入了向往已久的圣彼得堡大学,4年后因学习成绩优异,大学毕业被留校任教。
1885年秋,李雅普诺夫接受了哈尔科夫大学聘请,主持该校力学讲座。这期间虽与表妹见面不多,但思念酝酿了更加甜蜜和醇厚的爱情。1886年1月17日,李雅普诺夫来到圣彼得堡,与表妹举行了隆重婚礼。婚后夫妻俩形影相随,再也没有分开过。
娜塔莉娅是位高雅的艺术鉴赏家,对斯拉夫语言较感兴趣,曾翻译了多部塞尔维亚语作品。专业和生活情趣上的差异并未隔断两颗互相爱慕的心,相反倒使他们相互拓展了自己的学术视野。温柔美丽的妻子给李雅普诺夫的生活带来了欢乐,使之更加全身心地扑在教学和科学研究上。
1908年,李雅普诺夫应邀赴罗马参加第4届国际数学家大会,并会晤了在此养病的数学大师庞加莱(1854—1912年)。国际数学家大会现已成为全球数学界的盛事,其最引人注目的是颁发菲尔兹奖。第4届国际数学家大会第1次颁发的奖项是卡西亚奖,目的是推进代数挠曲线相关研究[1]。
时光荏苒,转眼李雅普诺夫夫妇已过银婚纪念日。沉浸在幸福之中的夫妇二人前往瑞士旅行。不幸的事情发生了,娜塔莉娅在旅行中感染了肺病,这在当时是不治之症。此时,李雅普诺夫的小弟已是敖德萨大学的斯拉夫语教授,希望黑海岸的温暖气候有助嫂子的身体康复,故盛情邀请兄嫂前来疗养。1913年李雅普诺夫夫妇来到敖德萨,经过一段时间的精心治疗和温馨呵护,娜塔莉娅的病情略有好转。
1917年春,李雅普诺夫夫妇到芬兰疗养,6月再度来到敖德萨。娜塔莉娅的病情越来越重,一再昏迷虚脱。心急如焚的李雅普诺夫为购买高价药品,答应在敖德萨国立大学开设《天体形状》讲座。因李雅普诺夫的学术声望极高,故其讲座一时轰动了整个校园。
1918年10月28日,李雅普诺夫正在进行第7次演讲,得知爱妻病危消息后,立即向听众致歉而回家。此时娜塔莉娅已到了弥留之际,李雅普诺夫俯在病榻前,眼泪止不住地流下来,双手紧紧握着爱妻之手,轻轻呼唤着其名字。最终娜塔莉娅在李雅普诺夫怀抱中安详离去。
李雅普诺夫悲痛欲绝,难以接受这残酷现实。他用手枪对着自己胸膛扣动了扳机。虽经家人奋力抢救,李雅普诺夫还是于1918年11月3日随爱妻而去。这就是俄罗斯版的梁祝。数学家也是人,也有血有肉,也有七情六欲,同样深深爱着自己的爱人,渴求永远守护着爱的永恒。李雅普诺夫的真情实感就是数学家对爱情的美丽诠释。
2 欲上九天揽新月在圣彼得堡大学留校任教后,李雅普诺夫仅用2年时间就通过了所有硕士课程考试,但其学位论文的选题却迟迟未定,为此他请教了圣彼得堡数学学派领袖切比雪夫。切比雪夫所建议的研究课题为:已知在角速度影响下,椭球体不再保持原旋转液团平衡形状。则在角速度略微增大时,其可能转变为哪些新平衡形状?这个貌似简单的科学问题,是当时学界公认的力学难题。其源于天体力学,牛顿、马克劳林(1698—1746年)、雅可比(1804—1851年)、柯瓦列夫斯卡娅(1850—1891年)等进行了一定探索,但皆未能取得实质性进展。
初生牛犊不怕虎。李雅普诺夫对该课题充满了浓厚兴趣,并展开了深入研究,但1年时间下来几乎没有多大进展。不过,该问题把李雅普诺夫引向椭球状旋转液团平衡形态的稳定性研究,并以此作为硕士学位论文研究内容。尽管该论文仅讨论了“切比雪夫问题”的一个特殊情形,但其学术价值很快就引起了科学界的极大关注。
在哈尔科夫大学任职后,李雅普诺夫对有限自由度力学系统平衡形状稳定性问题展开了研究,该问题是18世纪的研究热点之一。自1888年始,李雅普诺夫陆续发表了论文《有限自由度力学系统稳定性研究》《液体中刚体正规螺旋运动解析》《论具有周期系数的二阶线性微分方程理论若干问题》等,并由此撰写而成博士学位论文《运动稳定性一般问题研究》。
在博士学位论文中,李雅普诺夫给出系统稳定性的基本概念、研究方法和基本理论,包括稳定性分析两种基本方法,即李雅普诺夫第一方法、第二方法。
李雅普诺夫第一方法主要是通过分析非线性系统的线性化状态微分方程特征值分布来判定相关系统稳定性。对于较为复杂的非线性系统,李雅普诺夫则根据其平衡点附近线性化系统的稳定性,来判别它局部稳定性。即把非线性系统转化到其稳定点的线性化稳定。李雅普诺夫稳定性理论不仅适用于分析线性系统和非线性系统,了不起的是,其还能分析定常系统和时变系统的稳定性。不过随着相关研究系统维度的增加,其特征值会变得较为复杂,从而判定该系统的稳定性将会非常繁杂,因此李雅普诺夫第一方法适于低维线性系统或可线性化的非线性系统。
受“自治系统在运动过程中伴随能量变化”客观事实启示,李雅普诺夫创建了第二方法。该方法通过对相关系统构造一个类似能量的纯量函数,而考察该函数随时间变化来判断系统的稳定性。李雅普诺夫第二方法可适用于任意阶系统,而且不必求解系统状态方程来判定稳定性。李雅普诺夫定理表明,对于一个控制系统,若能找到一个正定函数,其导数是负定的,则该系统就是渐近稳定的。众所周知,对非线性系统和时变系统而言,求解其状态方程一般情形下都是较为困难的,这就充分显示出李雅普诺夫第二方法的优越性。在现代控制理论中,李雅普诺夫第二方法仍是研究系统稳定性的主要方法之一。
千淘万漉虽辛苦,吹尽狂沙始到金。直至1903年,李雅普诺夫关于天体形状的理论探索终于有了新突破,经过其30余年的不懈努力,终于圆满解决“切比雪夫问题”。首先,他以克莱罗方程作为相关理论体系的第一步近似,证明了近似球体平衡形状的存在条件,并将该问题转化为某微分方程组之解。第2年又在论文《关于行星形状理论的克莱罗方程及推广》中,继续深入研究该类微分方程组,严格证明了其中每个方程皆有一个满足某种自然条件的定解。在1905年发表论文《论一个切比雪夫问题》中,简要介绍了其整个研究过程和研究技术路线。而后以《近似于椭球体均匀旋转液团的平衡状态之研究》为题,分成4大部分内容,分别于1906年、1909年、1912年和1914年先后发表于《圣彼得堡科学院院刊》[2]。
在科学史上,李雅普诺夫第一个严格论证了近似于椭球体的新平衡状态存在性,而且达到所要求任何精度。他还找到了椭球数目与旋转液团倾角之间的密切关系,并给出2个马克劳林椭球和1个雅可比椭球的存在条件。他给出了若干近似计算方法,以简化天文学问题的计算复杂性,并创造了一系列巧妙数学方法来求解微分方程,充分展示了作者的深厚数学研究功底和娴熟数学方法技巧。
此后追求完美的李雅普诺夫,仍对“切比雪夫问题”锲而不舍,发表多篇论文来完善其相关理论。值得称道的是,李雅普诺夫1916年发表2篇论文——《近似于椭球体均匀旋转液团的表面方程探究》《近似于椭球体均匀旋转液团平衡理论新探》,应用数学工具证明了各种平衡存在性问题,并给出一些新平衡形状方程的构建模式。而在其遗稿《论非均匀旋转液团的某些平衡形状》中,已证得任何非分叉的马克劳林椭球或雅可比椭球皆可演化为新的平衡形状,其与原形状相近且保持角速度不变,但其密度呈现弱变化。
从1882年切比雪夫提出问题,30多年来李雅普诺夫始终考虑着该问题,直到离世。正如其言,切比雪夫影响了其一生的科学研究,这一方面表明了数学大师的高瞻远瞩,另一方面则说明李雅普诺夫能够“咬定青山不放松”。任何做学问者,绝不能打一枪换一个地方,只有“为伊消得人憔悴”之付出,方能达到“蓦然回首,那人却在灯火阑珊处”之境界。
3 随机世界求真诠在繁杂世界背后隐藏着何种规律,这是概率论探讨的主要课题之一。拉普拉斯(1749—1827)道:“生活中绝大部分问题其实只是概率问题。” [3]在概率论研究领域,李雅普诺夫继承和弘扬了切比雪夫概率思想,创建特征函数法来证明中心极限定理,实现了概率论极限定理研究方法的理论变革,奠定了近现代概率论基础。
在拉普拉斯概率理论基础上,切比雪夫对中心极限定理展开了研究。尽管他对中心极限定理的描述和证明尚存在一些缺陷,但这些逻辑上瑕疵掩盖不了其创造性的光芒,更加可贵的是,切比雪夫指明了概率论极限研究的新方向,将局部理论应用到概率论研究中,构造了矩方法来证明极限定理。马尔可夫深受切比雪夫的影响,对相关概率论课题产生了兴趣,并在恩师研究基础上,应用矩方法严格证明了中心极限定理。
李雅普诺夫对中心极限定理也很感兴趣,对于恩师和师兄的定理证明已拜读数次,虽从中受到了一些启发,但总是感觉其证明方法有些繁琐,而且定理条件有些苛刻。切比雪夫和马尔可夫是当时具有世界一流水准的概率论高手,若想突破他们的研究结果谈何容易。然而追求完美的李雅普诺夫,极力寻求更加一般的定理条件和更为简洁的定理证明。功夫不负有心人。李雅普诺夫终于找到了一个全新的突破口,即应用特征函数来证明中心极限定理。他高兴地写道:如此说来,定理的证明尚需继续研究,呼唤一个更加直接而简洁的证明,故我认为需要重新审视和考察定理的原来那些证明方法。……现在我已获得了一种新的定理证明方法。该方法不仅能够证明马尔可夫所说的切比雪夫定理,而且能够推广到更一般情形。这个一般结果的获得不过是在初等概率知识基础上应用了一个特殊工具[4]。
李雅普诺夫所说的这个特殊工具就是特征函数。随机变量X的特征函数定义变量eitx的数学期望。即对随机变量X作傅里叶变换,得到实变量复值函数。记为
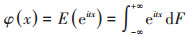
该积分值对任意实数t和任意分布函数F(x)皆收敛。
因相互独立随机变量和分布就是各加项分布之卷积,而在加项数目趋于无穷时,对卷积作数学处理较为困难,故切比雪夫和马尔可夫无法通过矩方法来考察其一般规律。由于李雅普诺夫突破了这个难点,因而特征函数成为研究极限分布的切入点。相对矩方法而言,特征函数法更具有一般性,其主要原因如下。
1)特征函数法要求条件更低一些,对于任意随机变量其特征函数皆存在,亦可用特征函数来确定分布函数各阶矩(若是存在的话)。
2)特征函数方法保留了随机变量分布律全部信息,而矩方法丧失了其中一部分信息。
3)随机变量之矩是否存在,皆可由特征函数唯一确定其分布函数,同时提供了特征函数收敛性质与分布函数收敛性质间一一对应关系。
4)相互独立随机变量和的特征函数等于相应随机变量特征函数之积。
因此,特征函数法为研究相互独立随机变量和的极限分布提供了简便有力的工具,现已成为解决随机变量之和问题的基本方法之一。
在1900年发表的论文《概率论的一个定理》中,李雅普诺夫证明了中心极限定理,其证明方法与现在用于素数理论方法相类似,并未像马尔可夫定理那样要求随机变量的所有阶矩一致有界,其唯一要求就是存在3阶矩。这就避免了矩方法要求高阶矩存在的苛刻条件。
在1901年发表的论文《概率论极限定理的新形式》中,李雅普诺夫试图再次减弱定理的条件。后李雅普诺夫又在2篇短文《概率演算中一定理的注释》和《概率演算中的一般命题》中指出,定理的条件可进一步“一般化”。
正是特征函数性质的灵活运用,使得李雅普诺夫圆满证明了所给中心极限定理。他利用特征函数精确描述了中心极限定理的条件,在概率论史上首次科学诠释了为何大多数随机变量皆近似服从正态分布的原因:现实世界中存在较多的随机变量,其为大量相互独立随机变量之和,且每个随机变量的作用很小。此外,这个随机变量之和的分布可为任意概率分布,而这种类型的随机变量在实际问题中经常发生。
相对于更一般的中心极限定理——林德贝格-勒维定理来说,李雅普诺夫定理更容易验证。如当随机变量序列的密度函数未知时,前者就无从着手,而后者仅需要求知道随机变量的2个数字特征就可以了。
李雅普诺夫的唯美追求成功不仅在于其简洁证明了中心极限定理,更在于其证明过程中所构造的独特新方法,为概率极限理论研究打开了一扇新窗口,实现了概率分析方法的重大革新,为极限定理进一步精确化研究奠定了理论基础[5]。
科学本质在于求真,力求揭示客观规律的真相。而真和美是密切相关的,美的科学理论更有可能是真的客观规律。李雅普诺夫虽然对一些世俗问题似乎格格不入,好像“不食人间烟火”的怪物,但对爱情始终执着专一,演奏了一曲动人心弦的诗篇。李雅普诺夫常常沉醉于科学问题,追求科学的至善至美。从而创立了运动稳定性理论和旋转液团平衡形状理论,探索了概率论中心极限定理和一系列其他深刻数学力学课题[6]。尤其值得赞美的是,李雅普诺夫所创立稳定性理论无论是在理论研究还是实际应用中均有着重要指导作用,引领了近半个世纪控制系统理论特别是非线性系统稳定性的研究方向。
| [1] | Gramer H. Half a century with probability theory: Some personal recollections[J]. The Annals of Probability, 1976, 4(4): 509-546. |
| [2] | 徐传胜.从博弈问题到方法论学科——概率论发展史研究[M]. 北京: 科学出版社, 2010: 186-216. |
| [3] | Todhunter I. A history of the mathematical theory of probability from the times of pascal to that of Laplace[M]. Cambridge, Londun: Macmillan, 1865. |
| [4] | Maistrov L E. Probability theory: A historical sketch[M]. New York, London: Academic Press, 1974: 188-216. |
| [5] | Sheynin Oscar. The theory of probability: Its definition and its relation to statistics[J]. Archive for History of Exact Sciences, 1998, 52(2): 99-108. |
| [6] | Hatvani L. Aleksandr Lyapunov, the man who created the modern theory of stability[J]. Electronic Journal of Qualitative Theory of Differential Equations, 2019, 26: 1-9. |