2019年8月6日,美国基础物理学突破遴选委员会宣布,奖金高达300万美元的基础物理学特别突破奖(Special Breakthrough Prize in Fundamental Physics)授予超引力理论的3位提出者,物理学家Sergio Ferrara、Daniel Z. Freedman和Peter van Nieuwenhuizen。本文介绍超引力的理论基础及研究背景。
1 基础物理问题现代科学发展,使人类对自然乃至整个宇宙有了非常深刻的理解。从空间角度,人类在原子核到太阳系尺度(10-15~1012 m)中掌握了基础物理的规律;从时间角度,人类已大致清楚了宇宙形成后10-11 s到100多亿年后的现在的整个演化过程。这些成就的高度概括就是基础物理学的两大理论支柱:量子力学和爱因斯坦的相对论[1-2],其中狭义相对论和量子力学可以完美地结合成量子场论。其中包含目前科学中最精确的理论——量子电动力学,它对电子磁矩反常的预言和实验的吻合达到了13位有效数字。以量子场论为框架的粒子物理标准模型给出了世界物质最基础的成分及其相互作用[3]。然而量子场论并不是个完整的理论,因为它不包含引力。事实上,它和描写引力的广义相对论很难结合,从而无法解决宇宙起源及黑洞奇点等问题。一个乐观的态度是,如果能够将引力和量子场论统一,那么将彻底揭开世界最基本层次的所有奥秘。这也许是为什么量子引力这个课题那么引人入胜。物理学发展的方法可以粗略划分为两大类:“从上而下”和“自下而上”。物理学发展史上从伽利略、牛顿的经典力学到20世纪的量子力学,物理理论的建立绝大部分可以归为“自下而上”,利用大量实验,总结推出物理定律;而爱因斯坦的广义相对论应归为“从上而下”,许多关键的预言到100年以后才获得天文观测的证实[4]。另一个典型并著名的“从上而下”的例子是杨-米尔斯理论[5],该理论在1954年提出时并没有任何实验的动机,但后来杨-米尔斯理论成为描写基本粒子相互作用必不可少的部分。
实验证据表明,这个世界有着巨大的能标落差,2个质子间的静电排斥库仑力是牛顿万有引力的1020倍。这意味着,以量子场论为基础的粒子物理在小于1016 GeV(1 GeV=109 eV)能标时不需要考虑引力效应,而目前的实验能标最高只能做到近103~104 GeV。因此,目前实验不可能像20世纪量子力学时代那样“手把手”地指导量子引力研究的进程。这是任何一个量子引力理论都必须面对的现实,但是放弃从来不是人类的天性,“从上而下”也就成为这个方向发展的重要手段。
2 基础物理方法及原则是什么具体方法和原则使基础物理胜出,让人类对世界的本质取得如此深刻的理解?基础物理研究的主导哲学思想是还原论[6],通过什么(what)、怎样(how)和为什么(why)这3个问题来研究世界。也就是,世界最基本的构成是什么?它们是如何相互作用的?为什么是这个性质?对前2个问题现代粒子物理有了较好的回答。粒子物理标准模型认为,所有的物质是由最基本的夸克和轻子组成,而它们之间的相互作用可以包含人类平时可以感受到的电磁相互作用,以及一般在平时生活中不能也不希望感受到的原子核强相互作用及弱相互作用。引力在目前实验可到达的微观尺度可以被忽略,但是由于在大尺度上电荷是中性的,而且原子核相互作用是短程的(10-15 m),因此在宏观世界由广义相对论所描述的引力成为主导。
值得强调的是,还原论的思想在基础物理的研究中获得了充分体现。物理学是一门“统一”的科学:苹果落地和行星运动的动力根源统一成万有引力;摩擦取“磁”和闪电都是电;电和磁统一成麦克斯韦的电磁理论。物质的构成、相互作用所体现的形形色色的所有自然现象,也许可以用几个乃至一个基本的理论来统一描述。
但是世界为什么是这样?这个问题没有一个标准答案。这涉及到人类认知的一个有趣的问题:当我们说搞懂了一个物理现象时,这个“懂”是什么意思。是因为我们能精确地用实验重复出理论预言吗?事实上,量子力学的实验验证要比牛顿力学精确的多,但大部分物理学家会毫不犹豫地说他们懂牛顿力学,却不会轻易说懂量子力学。
也许应该从对称性角度来理解基础理论。自古以来,自然中展现的对称性,尤其是几何对称性,一直吸引专家及公众的好奇之心,但伽利略第一个认识到连续对称性对动力学的重要性[7]。牛顿力学包含时空平移及空间转动对称性,而狭义相对论则是在此基础上添加了时空转动不变性,即洛伦兹对称性[8]。这些对称性是直观的,可以用一定的坐标变换精确描述,物理规律则不会因相应的坐标变化而改变。广义相对论更是把这个概念推广,认为物理规律不会因坐标的任意变换而改变。自然界的规律往往是简单的,这种简单性的背后都有对称性的影子,成功的基础理论往往是某个对称性下一个最简单理论。事实上爱因斯坦的广义相对论可以认为是在广义坐标变换下不变的最简单理论。同样,麦克斯韦电磁学和杨-米尔斯理论分别是阿贝尔和非阿贝尔规范对称性下的最简单理论,粒子物理标准模型受到狭义相对论、阿贝尔及非阿贝尔规范对称性的强力限制。
一个例外是量子原理。虽然一个具体的量子力学模型有相应的对称性,但量子特有的现象产生的机制似乎并不起源于对称性原理,没有人能够通过某个对称性把量子力学令人信服地推导出来。这也许是为什么,尽管没有任何实验给出量子原理的丝毫偏差,还是有大量物理学家说我们并没有“真正”搞懂为什么我们的世界是量子的。量子原理还不能叫理论,有多种“诠释”。至于世界为什么是量子的,没有一个更基本层面的解释,而是实验结果“强加”给我们的。也许一种更合理的观点应该是,既然量子原理是更基础的,那么要解释的不是为什么这个世界是量子的,而是为什么这个世界看上去是经典的。
由此可见,现在被实验充分证实的基础物理定律似乎都遵循以下2个规则:量子原理和恰当的对称性。量子原理和狭义相对论与规范对称性都可以完美结合,给出了描写粒子物理标准模型的量子场论,但是目前它还无法和广义相对结合成一个自洽的量子引力。当量子原理和对称性发生碰撞时,应该修正哪一个呢?量子原理的逻辑非常紧密,要么彻底推翻,要么全盘接受,而对称性这个概念大有可操作的余地。
物理学还原统一的进程体现在对称性的层次结构。经典力学中的伽利略对称性包含于狭义相对论中的庞加莱对称性,而其又是广义坐标变换的一部分;阿贝尔规范对称性包含于非阿贝尔规范对称性;整体对称性包含于局域对称性。事实上,广义相对论可以认为是狭义相对论庞加莱整体对称性局域化的结果。正是因为这些层次结构,当一个新理论推翻旧理论时,我们并不把旧理论抛弃。
3 量子力学和超对称那么如何推广现在所知的对称性呢?即使在爱因斯坦的广义相对论框架下,时空和物质依然相对独立,其表现在物质的内禀对称性与时空对称性无关。因此一个自然的推广就是把这2种截然不同的对称性统一起来。早在20世纪20年代,Kaluza和Klein就发现电磁场可以起源于5维的纯引力[9-10],在这个框架下,电磁场的规范对称性是5维时空坐标变换的一部分。1953年,泡利研究6维广义相对论,发现如果内禀空间是2维球时,4维的有效理论就含有杨-米尔斯在1954年提出的非阿贝尔SO(3)场。由于结论太惊世骇俗以及数学上的不成熟,泡利只做了2个报告,而没有发表文章[11]。直到2004年,泡利的思想在6维超引力的框架下[12]才完全实现[13]。这些结果的重要性在于,一些特定理论的物质场固有的阿贝尔或非阿贝尔规范对称性可以成为高维广义坐标变换的时空几何对称性,从而揭露时空对称性和物质内禀对称性是可以相关联的。
但是以上对称性的推广都需要借助高维时空,而且局限于规范场的局域对称性。如何把所有物质的内禀性质和时空对称性联系起来,量子力学给出了答案。虽然量子力学并不基于对称性,但它可以给出新的对称性。量子原理有几条普遍预言:波函数或态,测不准原理,几率测量及全同粒子。其中全同粒子概念是世界也许有个终极理论的最重要依据。如果宇宙中大约1080个电子的内部固有性质都不相同,那么“终极理论”的复杂度就难以想象。全同粒子的预言意味着描写物质的场概念比粒子更基本,是量子场论的基础。我们这个世界只有一种电子场或电磁场,它们的量子激发给出了存在于世界各处形形色色但必然内禀全同的电子和全同的光子。这就是为什么物质世界的基础理论——粒子物理标准模型可以仅用几行公式完全给出。
由于量子力学中的态或波函数不能直接测量,只有它们模的平方才是可测量的物理量,因此量子力学的全同粒子概念预言有2类不同的统计性质的粒子。一种叫费米子,服从费米-狄拉克统计,遵守泡利不相容原理;另一种叫玻色子,遵循玻色-爱因斯坦统计,不遵守泡利不相容原理,在低温时可以发生玻色-爱因斯坦凝聚。在粒子物理标准模型中,代表物质的轻子与夸克都是自旋为半整数的费米子,而描写物质间相互作用的场所激发的都是自旋为整数的玻色子。
在基础物理研究中,2个貌似截然不同甚至相反的概念往往可以统一起来。电与磁的统一已被广为接受;量子力学的波粒二象性依然非常反直觉。那么费米子和玻色子之间是否也有内在关系?这个关系就是超对称。超对称是一种可以把费米子和玻色子互为变换的对称性,这个粒子或场的内禀对称性却又可以和量子场论中的庞加莱时空对称性结合起来。这个结合可以直观地想象:当把超对称作用在某个时空点上的一个费米子时,它变成玻色子;如果再作用一次,又变回了费米子,但它不一定还处在原来的时空点,可以在时空中产生平移。用数学描述,超对称的变换性质就是其生成元Qα的以下反对易关系[14]:
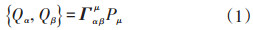
其中,Pμ是时空平移生成元,Γμ是狄拉克伽马矩阵。
这样以上所有的物理思考变成了一个严格的数学问题:包含洛仑兹变换的庞加莱代数是否有自洽的超对称推广?答案是肯定的。在20世纪80年代,所有的超对称李代数都已经被构造并归纳。超对称的一个全新性质是它首次把所有粒子的内禀对称性和它们所处时空的对称性联系起来,因此超对称的性质必然和时空维数有关,而非常有意思的是,允许超对称代数的最高时空维数是11维。
4 超引力超引力如其名所示,似乎可以简单地理解为超对称和爱因斯坦引力的结合,但事实上,前者可以推导出后者。庞加莱对称性是整体的,对它的局域化必然可以获得描写引力的爱因斯坦广义相对论。量子力学中的全同费米子和玻色子,可以导出整体超对称,而超对称包含庞加莱对称性,因此有局域超对称的理论必然包含爱因斯坦引力,称之为超引力。
历史上,超对称是在粒子物理学中首先提出的。1966年,日本物理学家宫沢弘成提出了强子物理中(费米)重子和(玻色)介子的超对称关系[15],但他没有意识到超对称和时空对称性的关系,在当时他的工作几乎被忽略。1971年,法国物理学家Gervais和日裔崎田文二合作在2维量子场论的框架下通过阶化李代数重新发现超对称,使超对称场论建立在严格数学的基础之上[16]。但最关键的4维时空超对称代数是1974年由德国物理学家Wess和意大利物理学家Zumino合作获得的[14],同年,他们构建了超对称拉格朗日模型[17],在此基础上,法国物理学家Fayet在1977年提出了标准模型的超对称化,称为最小超对称标准模型(MSSM)[18],从而使超对称理论和粒子物理实验联系起来,形成超对称粒子物理现象学这个研究领域。非常遗憾的是,至少在103 GeV能标中粒子物理实验(大型强子对撞机,LHC)上并没有发现超对称迹象。
把超对称的整体对称性局域化由美国物理学家Arnowitt和Nath在1975年首先提出,他们称之为规范超对称[19],但第一个超引力理论,也就是4维最小超引力的构造由美国大学物理学家Freedman、van Nieuwenhuizen和Ferrara在1976年完成[20]。他们因此获得2019年的基础物理学特别突破奖。超引力的一个重要预言是自旋为3/2的基本粒子。在粒子物理学标准模型或最小超对称标准模型中,基本粒子的自旋可以是0、1/2或1,而爱因斯坦引力中的引力子自旋为2,唯独缺少的是自旋为3/2的费米子。也许可以想当然地在标准模型中加入这样一个粒子,但可以证明自旋3/2的自由费米子不能和引力自洽耦合,而超引力是该粒子和引力耦合的最简单理论[21]。自旋3/2费米子非同寻常的性质,意味着如果在实验上发现它的存在,也基本证明了超引力的正确性。在超引力中,该粒子叫引力微子(gravitino),它的质量体现了超对称破缺的能标,目前的实验限制是必须在103 GeV以上。引力微子是目前暗物质的候选者之一。
随后10余年,不同时空维度的超引力被物理学家逐个构造出来[22],除了最近的研究[23];没有中国物理学家参与超引力的构建工作。利用超对称代数构造超引力并不需要太强的“创新”能力,但需要扎实的数学功底和极其耐心的计算能力。许多超引力构造的草稿都是写得密密麻麻的A2素描纸,因此超引力的构造基本上都是由稳健的欧洲学者完成,很少甚至没有出自哈佛或普林斯顿。最重要的超引力也许是法国物理学家Cremmer、Julia和Scherk在1978年构造的最高时空维数所允许的(唯一的)超引力,也就是11维超引力[24]。结果发现,几乎所有的低维超引力都可以嵌入到11维超引力之中,这体现出11维时空的特殊性。对于寻找终极理论的学者来说,一个唯一的,但又可以推导出任何别的理论的母理论无疑是非常有吸引力的,然而11维超引力理论的热点在20世纪80年代末逐渐消亡。一方面,它不能给出粒子物理标准模型,尤其是不能产生当初还认为是质量为零的中微子;在宇宙学应用中,它们给出了与观测不符的巨大的宇宙学常数[25-26]。另一方面,它也不能解决爱因斯坦引力的不可重整化这个纯理论问题,从而不是一个自洽的量子引力。虽然这些问题在后来的研究中获得了大量改善,但是超引力研究的重新兴起及重要性离不开超弦理论这个框架。
虽然量子场论中物质由场描述,但它的量子激发态是局域的空间0维度的点粒子形态。弦理论认为物质的最基础形态是尺度为普朗克长度(10-33 m)的1维的弦而不是0维的点。这么一个貌似普通的推广,却要求弦所在的时空必须有动力学,从而自然而然地包含了爱因斯坦的广义相对论。研究发现弦理论的数学自洽性,要求理论有超对称,而且超弦理论的时空背景必须满足超引力的运动方程。这使超引力成为超弦研究的一个不可分割的部分。然而由于微扰超弦理论的最高时空维度是10维,这使11维超引力在80年代末开始备受冷落。美国学术界一贯追求热点的风气和压力使11维超引力的研究当时在美国一流大学几乎无人问津。但还是有一部分欧洲学者坚持认为11维超引力的重要性,其代表人物是Michael Duff[27]。这种坚持最后得到了回报,11维超引力最后成为超弦的母理论(M-theory)最重要的组成部分。
5 从超对称到爱因斯坦引力用数学来显示局域的超对称理论必然包含爱因斯坦广义相对论。一个自旋为3/2的费米子可以用带时空指标的狄拉克费米场ψμ来描写,在任意弯曲时空中,它的拉格朗日量为

其中,g是时空度规的行列式,Dυ是时空协变导数,Γμυρ是狄拉克矩阵的3阶全反对称乘积,最后一项代表被省略的4阶费米项。
这是自旋1/2狄拉克费米子理论的自然推广,时空虽然可以是弯曲的,但它只是一个固化不变的背景,因此并没有把广义相对论包含进来。与自旋1/2的费米子不同的是,该理论的自洽性要求必须存在ψμ的4阶项。在局域超对称变换下,δψμ = Dμε,忽略高阶费米项,拉氏量的变化是
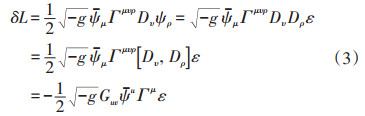
在这里,描述爱因斯坦时空动力学的爱因斯坦张量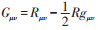 在超对称变换下出现。这就意味着超引力必然包含
在超对称变换下出现。这就意味着超引力必然包含
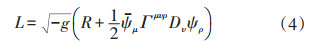
其中第1项就是爱因斯坦-希尔伯特量。可以证明,这个理论在不超过费米子平方项的近似下,在下面的超对称变换时是不变的:
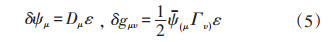
然而,引力微子ψμ和引力的耦合必须包含4阶费米项,而且还必须证明这个超对称变换可以形成封闭的李代数。这些使没有经过专业训练的人很难构造超引力。这个工作由Freedman、van Nieuwenhuizen和Ferrara在1976年完成,而该超引力是自旋3/2费米子和引力自洽耦合的最简单理论。
6 结论如果说超对称的提出是试图直接解决粒子物理标准模型中的能标的不自然性、规范耦合常数统一及暗物质等问题,那么超引力的构造是纯粹“从上而下”的运用,充分体现了物理学家在基础研究中的不可缺少的想象力,同时又给出一个可以通过实验检测的自旋3/2费米子的预言。它的研究犹如打开了潘多拉的魔盒,给出了一个目前数学技术尚无法驾驭的超弦这个庞大的理论框架。
超弦理论研究给了我们规范/引力这个可以有实际运用的全息对偶关系[28],但是超引力及超弦理论能否成为世界的基础理论还远远没有获得证实。宇宙给了人类一个1016能标差的量子引力问题,我们无从逃避。基础物理学特别突破奖授予超引力理论的提出者,是对“从上而下”研究的一种认同和鼓励。正如该奖创始人之一Yuri Milner所评价“:当我们提起有关人类想象力的伟大作品时,我们往往会指向艺术、音乐或文学,但是最深刻和最优美的是科学家的创作。几十年来超引力一直在启发物理学家的灵感,它很可能包含现实本质的深刻真相。”
致谢 庞毅、刘海山及马良对初稿提出了大量修改意见。
| [1] | Einstein A. Zur Elektrodynamik bewegter Körper[J]. Annalen der Physik. 2006, 322(10):891-921. |
| [2] | Einstein A. The field equations of gravitation[J]. Sitzungsber. Preuss. Akad. Wiss. Berlin (Math Physics), 1915:844-847. |
| [3] | Oerte R. The theory of almost everything:The standard model, the unsung triumph of modern physics[M]. New York:Pi Press, 2006:327. |
| [4] | Abbott B P, Abbott R, Abbot T D, et al. Observation of gravitational waves from a binary black hole merger[J]. Physical Review Letters, 2016, 116(6):061102. |
| [5] | Yang C N, Mills R L. Conservation of isotopic spin and isotopic gauge invariance[J]. Physical Review, 1954, 96(1):191-195. |
| [6] | Ruse M. Entry for ‘reductionism’[M]. 2nd ed. The Oxford Companion to Philosophy. Oxford:Oxford University Press, 1995:793. |
| [7] | Galilei G. Discorsie dimostrazioni matematiche, intorno á due nuoue scienze (in Italian)[M]. Leiden:Elsevier, 1638:191-196. |
| [8] | Lorentz H A. Electromagnetic phenomena in a system moving with any velocity smaller than that of light[C]. Proceedings of the Royal Netherlands Academy of Arts and Sciences, 1937:172-197. |
| [9] | Kaluza T. Zum unitätsproblem der physik[J]. Sitzungsber. Preuss. Akad. Wiss. Berlin (Math. Phys.), 1921:966-972. |
| [10] | Klein O. The atomicity of electricity as a quantum theory law[J]. Nature, 1926, 118(2971):516. |
| [11] | Straumann N. On Pauli's invention of non-Abelian Kaluza-Klein theory in 1953[C]//Ninth Marcel Grossmann Meeting:On Recent Developments in Theoretical and Experimental General Relativity, Gravitation and Relativistic Field Theories, 2002, 3:1063-1066. |
| [12] | Salam A, Sezgin E. Chiral compactification on Minkowski×S2 of N=2 Einstein-Maxwell supergravity in six dimensions[J]. Physics Letters B, 1984, 147(1):47-51. |
| [13] | Gibbons G W, Pope C N. Consistent S2 Pauli reduction of six-dimensional chiral gauged Einstein-Maxwell supergravity[J]. Nuclear Physics B, 2004, 697:225-242. |
| [14] | Wess J, Zumino B. Supergauge transformations in fourdimensions[J]. Nuclear Physics B, 1974, 70:39-50. |
| [15] | Miyazawa H. Baryon number changing currents[J]. Progress of Theoretical Physics, 1966, 36(6):1266-1276. |
| [16] | Gervais J L, Sakita B. Field theory interpretation of supergauges in dual models[J]. Nuclear Physics B, 1971, 34:632-639. |
| [17] | Wess J, Zumino B. A Lagrangian model invariant under supergauge transformations[J]. Physics Letters B, 1974, 49:52-54. |
| [18] | Fayet P. Spontaneously broken supersymmetric theories of weak, electromagnetic and strong interactions[J]. Physics Letters B, 1977, 69:489-494. |
| [19] | Nath P, Arnowitt R L. Generalized supergauge symmetry as a new framework for unified gauge theories[J]. Physics Letters B, 1975, 56:177-180. |
| [20] | Freedman D Z, van Nieuwenhuizen P, Ferrara S. Progress toward a theory of supergravity[J]. Physical Review D, 1976, 13:3214-3218. |
| [21] | van Nieuwenhuizen P. Supergravity[J]. Physics Reports, 1981, 68:189-398. |
| [22] | Salam A, Sezgin E. Supergravities in diverse dimensions[M]. Singapore:World Scientific, 1989:1499. |
| [23] | Novak J, Ozkan M, Pang Y, et al. Gauss-Bonnet supergravity in six dimensions[J]. Physical Review Letters, 2017, 119(11):111602. |
| [24] | Cremmer E, Julia B, Scherk J. Supergravity theory in eleven-dimensions[J]. Physics Letters B, 1978, 76:409-412. |
| [25] | de Wit B, Nicolai H, Warner N P. The Embedding of gauged N=8 supergravity into d=11 supergravity[J]. Nuclear Physics B, 1985(255):29-62. |
| [26] | Cvetič M, Lü H, Pope C N. Four-dimensional N=4, SO (4) gauged supergravity from D=11[J]. Nuclear Physics B, 2000(574):761-781. |
| [27] | Duff M J. Ten to eleven:It is not too late[M]. Supersymmetry and Quantum Field Theory、Berlin, Heidelberg:Springer, 1997:59-63. |
| [28] | Maldacena J M. The large N limit of superconformal field theories and supergravity[J]. International Journal of Theoretical Physics, 1999(38):1113-1133. |