2. 中国科学院大学,北京 100049
3. 中国科学技术大学物理学院,合肥 230026
4. 北京师范大学天文系,北京 100875
2018年3月14日,当今享有盛誉的物理学家斯蒂芬·威廉·霍金(Stephen William Hawking,1942—2018)(图 1)去世的消息震惊世界。霍金独特的人生及其在物理学研究上的成就,在人们心中树立了一位伟大科学家的形象。特别是自出版以来已被翻译为40多种文字、累计销量达2500万册的科普巨著《时间简史》为霍金带来了无数的追随者。而在物理学术界,霍金同样是非常卓越的科研巨才,在他的学术生涯中共发表了160多篇学术论文,被引用达4万多次。他所创造的理论、证明的公式和定理,为人类理解时空、黑洞和宇宙等打开了一扇窗口。
 | 图 1 斯蒂芬·威廉·霍金(1942—2018) Fig. 1 Stephen William Hawking (1942—2018) |
霍金无论是在学术贡献上,还是在科学普及和科学文化传播上,都配得上当今一位伟大物理学家的称号。斯人已逝,他所创造的物理理论,发表的学术工作,出版的科学著作无疑是他留给我们的宝贵财富。这里通过梳理霍金生平的学术工作,简要介绍霍金在物理学研究上的学术贡献。
霍金的研究工作涉及引力理论中很多重要的问题,但他主要的研究对象和贡献集中在黑洞物理和宇宙学。无论在经典引力还是半经典量子引力的层次上,霍金的工作几乎都是开创性的。这里分两部分介绍霍金在学术上的贡献:第一部分,以时间顺序简述霍金的主要学术工作和取得的成就;第二部分,简述霍金的这些学术工作对一些相关领域的启发和影响,例如引力全息性质和引力波物理等。
1 霍金生平学术1.1 经典的极致(1962—1973)
如同早期人类只关注于自己周围一样,20世纪60年代以前人们关于广义相对论的研究主要集中在时空的局部性质。直到20世纪60年代以后,彭罗斯(R. Penrose)、霍金、盖罗奇(R. Geroch)等才开始利用现代数学工具来研究时空的整体性质。霍金在这方面的研究始于其攻读博士学位期间,这可从他的博士论文[1]——《Properties of Expanding Universe》(《膨胀宇宙的性质》)——中觅得一二。该论文分为四部分:第一部分对霍伊尔(F. Hoyle)等的引力理论(稳恒态宇宙)进行了批判,强调了膨胀宇宙的重要性;第二部分研究了宇宙微扰理论;第三部分研究了膨胀宇宙中的引力辐射;第四部分是关于宇宙奇点问题的研究。这里,我们着重介绍第三和第四部分。在第三部分,霍金研究了宇宙中渐近Fridemann-Robterson-Walker模型的时空区域中的引力辐射问题。当我们感兴趣的时空区域的尺度远小于哈勃尺度时,建立在类光无限远渐近平坦时空中的引力辐射模型是很好的近似;但在宇宙学中,我们关注的时空区域往往接近于宇宙学尺度,宇宙背景的演化会对引力辐射具有不可忽视的贡献。这便需要一个研究引力辐射的准局域模型。为此,霍金给出了一个重要的关于引力系统准局域能量的定义,被后人命名为霍金质量。这一质量演化的单调性在说明引力辐射(引力波)是否携带能量的问题上给出了准局域的解释,可看成是1962年邦迪(H. Bondi)等关于引力辐射携带能量整体论证[2]的一个准局域补充。第四部分的内容旨在证明宇宙中奇点的普遍存在性,而与对称性没有关系。事实上,早在20世纪30年代,基于爱因斯坦(A. Einstein)的广义相对论,奥本海默(J. Oppenheimer)和斯奈德(H. Snyder)已经证明球对称星体必然会坍缩到时空的奇点,只要星体的质量足够大[3]。60年代,彭罗斯证明即使没有球对称条件,引力坍缩中也必然存在奇异性[4]。霍金考虑了与引力坍缩相反的过程,即宇宙的膨胀。他证明:当物质场满足强能量条件,描述宇宙的时空满足整体双曲等条件,则过去指向的类时测地线必然不完备。换句话说,时空必然存在奇异性。这一研究可以说是“大爆炸”宇宙模型的理论基础。这些工作被他和合作者不断完善和推进,陆续发表在相关学术杂志上。例如,1970年他和彭罗斯合作完成的关于引力塌缩和宇宙中奇异性定理的证明进一步放松了证明的条件[5]。从某种意义上说,这些研究表明了爱因斯坦引力理论的不完备性,激发了人们关于量子引力的研究。正如霍金所期待的:在量子引力的层次上奇点或许并不存在。
20世纪60年代末,关于黑洞经典性质的研究取得了很大的进展。其中最重要的发现当数黑洞的简单性:黑洞可以由质量、角动量和电荷所决定。这就是人们常说的黑洞无毛定理[6]或黑洞唯一性定理[7-9]。这里的“毛”是指黑洞的守恒荷。黑洞唯一性定理的证明需要很多引理性的子定理。其中刚性定理和拓扑唯一性定理是重要的组成部分:稳态黑洞要么是静态,要么是轴对称的,以及黑洞事件视界的截面在拓扑上是个二维球面。霍金在1972年完成了这两个子定理的证明[10],为黑洞唯一性定理的证明铺平了道路[11-13]。1971—1972年,霍金证明了黑洞事件视界截面的面积不减定理[10],1973年又与巴丁(J. Bardeen)、卡特(B. Carter)建立了黑洞力学四定律[14]。这些研究不仅为用几个参数(几根毛)描述黑洞提供了严格的理论基础(例如,LIGO理论分析中关于黑洞的描述[15]),也给出了两个黑洞并合过程中引力辐射能够携带出能量的上限[16]。1973年,霍金和埃利斯(G. Ellis)的《时空的大尺度结构》一书出版[17]。它用公式和定理详尽描绘了霍金和他的同事们所创造的从20世纪60年代初到70年代初广义相对论研究的黄金岁月。
霍金等的这些研究,启发了人们关于黑洞量子性质的研究。例如,贝肯斯坦(J. Bekenstein)基于霍金的黑洞面积不减定理,提出黑洞有熵,且正比于黑洞视界截面的面积[18]。
1.2 量子论的光辉(1974—1980s)不仅霍金,当时的很多物理学家都不接受贝肯斯坦的观点:黑洞有熵,就需要有温度;有了温度,黑洞就会辐射。但任何物体都不能逃离黑洞,不可能有辐射,因此不可能有温度。1973年底,霍金考虑了黑洞背景上场的量子效应,他发现黑洞的确会辐射粒子(被后人称为霍金辐射)(图 2),且无限远处观测者看到辐射粒子的谱是一个黑体谱,相应的温度正比于黑洞的表面引力[19]。这就是黑洞的霍金温度。霍金在确认计算的正确性后,接受了贝肯斯坦的观点,并给出了黑洞熵的准确表达式[20]。这个熵被称为贝肯斯坦-霍金熵。霍金的工作将黑洞力学提升为黑洞的热力学,这成为他一生中最为重要的一个工作。
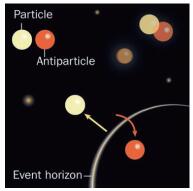 |
图 2 霍金辐射常见的“正反粒子对”解释 (图片来源:https://www.sciencenews.org/article/black-holes-bathtub) Fig. 2 Usual explanation of particle and its anti-particle in Hawking radiation |
霍金和杰彭斯(G. Gibbons)等随后发展的欧几里德量子引力是研究黑洞热力学性质最为系统的理论[21-22]。在该理论中,量子引力的路径积分形式可给出引力系统所需热力学系综的配分函数。霍金在这些研究中的贡献是巨大的。一些简单的名词即可说明问题。例如在鞍点近似下,引力系统的欧几里德作用量对应于热力学势。很多情况下,单纯的希尔伯特-爱因斯坦作用量并不能给出正确的欧氏作用量。这时需要考虑杰彭斯和霍金引入的使得变分问题自洽的项,即杰彭斯-霍金项[21]。黑洞的热力学稳定性,热力学相变,以及更一般的引力瞬子的热力学也被广泛研究[22]。例如,在anti-de Sitter(反德西特)引力中,著名的霍金-佩吉(D. Page)相变[23]近年来愈被人重视,因为它在理解强耦合场论的性质方面得到广泛应用。霍金的工作掀起量子引力理论的零级近似,即弯曲时空上量子场论研究的热潮,也为检验一个量子引力是否成功提供了一个公认的标准——能否在量子统计的层次上解释黑洞的贝肯斯坦-霍金熵。无论是后来的弦理论还是圈量子引力,都需要经受这一检验[24]。
黑洞是一个热力学系统,但不同于普通物质的热力学。最明显的一个特征是:贝肯斯坦-霍金熵正比于黑洞视界的面积,而不是体积。近20年来,基于霍金和贝肯斯坦的熵公式,人们提出了引力的全息性质——一个引力系统等价于其边界上没有引力参与的一个量子系统,并成为高能物理和引力理论研究中最为活跃的领域之一。无论在时空观的变革还是引力本质的理解上,引力的全息性质都提供了深刻的启示。引力的这一性质可以说是霍金关于黑洞研究的延伸,并成为量子引力的一个基本原理。
1.3 信息丢失疑难(1974—2018)黑洞的霍金辐射意味着黑洞具有熵,它解决了惠勒(J. Wheeler)提出的存在黑洞的宇宙中总熵丢失的问题。但霍金辐射的存在同时又提出了信息丢失的疑难。由能量守恒,霍金辐射使得黑洞质量不断减少,最终黑洞会变成一堆热辐射。这就是黑洞的蒸发。事实上,霍金在1975年便已经研究了黑洞蒸发的问题[20]。随后他的学生佩吉具体研究了由霍金辐射所引起的黑洞演化[25-27]。假定在无限远过去形成黑洞的物体处于纯态,黑洞形成并蒸发后,系统完全处于混合态。这样,形成黑洞物体的信息丢失了,这就是黑洞的信息丢失问题。由纯态到混合态,这是一个非幺正的过程。因此黑洞的形成和蒸发破坏了量子理论中的幺正性。关于信息是否丢失问题,学术界仍有不同观点,但主流观点是信息没有丢失。这主要是受到引力的全息性质,或更为具体的引力/规范场对应的影响。因为按照引力/规范场对应,引力系统等价于其边界上的量子场论,引力演化过程原则对应于量子场论中的幺正过程。从这个意义上来说,所谓的信息丢失问题最终归结为如何恢复信息的问题。至今为止,人们已提出很多恢复信息的方案。2016年,霍金、斯特罗明格(A. Strominger)和佩里(M. Perry)提出黑洞除了具有质量、角动量、电荷这些毛之外,还可能具有软毛(soft hair)[28]。因为BMS(Burg-Metzner-Sachs)超平移对称性预示了对于所有的引力理论在渐进闵氏空间上有无穷数量的守恒律。这些守恒律需要黑洞携带大量的软(零能)超平移毛。而这些软毛可以携带信息。一些信息被以软引力子或软光子的形式存储在位于视界未来边界的全息盘上。当然,黑洞的软毛是否可以解决信息丢失的问题仍然有很多争议,需要进一步研究。而黑洞的信息丢失问题将仍是每个可能的量子引力理论必然要面对的问题。
1.4 量子宇宙学(1983—1990s)除了在黑洞方面的研究,霍金在宇宙学上还有一些著名的工作。例如,20世纪80年代,人们已经意识到早期宇宙不可能是严格的均匀和各向同性,否则无法形成星系,这涉及宇宙的初值或边值问题。但无论在热大爆炸还是暴涨模型中,初值问题都是以某种假设的形式存在。1983年,霍金和哈特尔(J. Hartle)提出用宇宙波函数描述空间闭合宇宙的量子态[29]。
这个波函数是宇宙的三维(闭合的)空间S的度规hij和物质场在其上取值的泛函,并满足正则量子引力中的惠勒-德威特方程。众所周知,一个量子系统的基态或最低激发态可由系统的欧几里德位形的路径积分表示。类似地,在正则量子引力理论中,宇宙的基态可以表示成边界为S且在S上诱导度规为hij的四维黎曼流形上度规和其他可能场的路径积分形式(度规具有欧几里德号差,通常的相对论性时空为度规具有洛伦兹号差的洛伦兹流形)。这个路径积分涉及到满足上述条件的所有可能的四维几何的贡献。由量子理论的解释,这个积分的意义是明确的:给出了宇宙由无(S “收缩”为一点的情况)到有的概率幅。霍金和哈特尔要求这个四维流形是紧致的,否则会有波函数无法归一化的问题。因此,在霍金和哈特尔看来,在欧几里德层面上宇宙没有时间和空间的边界(图 3)。宇宙的初值或边值问题被没有边界而巧妙地回避。这样,在大爆炸之前,时间并不存在,因此诸如对宇宙开始的诘问是没有意义的。正如他本人打的形象比喻,就像诘问北极点之北那样没有意义。
 | 图 3 无边界宇宙(图片来源:www.reasonablefaith.org) Fig. 3 No boundary universe |
基于此路径积分描述宇宙量子态的方案,霍金及其合作者在随后工作中研究了宇宙结构起源问题,指出:宇宙结构不是起源于具有任意性的初条件,而是起源于由海森堡不确定性原理给出的基态的涨落[30]。
尽管正则量子引力理论在20世纪60年代已经被人们广泛研究,但霍金等的量子宇宙模型输入了新的内容:利用欧几里德路径积分构造基态和可能的激发态;而无边界假设真正第一次从量子引力角度诠释了宇宙的初值问题。这一工作为后来人们从各种具体的量子引力模型(如弦理论和圈量子引力)研究宇宙初值问题等奠定了基础。
1.5 其他工作另外,霍金在原初黑洞[31]、虫洞[32]、正质量定理[33]、引力的全息性质[34]及膜世界图像[35]上也有一些重要工作。总体看来,他的研究工作基本处于引力理论研究引领位置。当然,现在看来,霍金最为重要的工作是1974年关于霍金辐射和黑洞热力学的研究。这一工作影响深远,为我们理解引力本质打开了一扇明亮的窗口。
2 霍金工作的启发和影响2.1 引力全息性质
受黑洞贝肯斯坦-霍金熵的启发,1994年,胡夫特(G. t'Hooft)[36]和萨斯坎德(L. Susskind)[37]提出引力具有全息性质的概念:一个引力系统的独立自由度由它的边界面积来测度。1997年底,马尔德西纳(J. Maldacena)在弦理论中精确地实现了这一思想[38]:AdS5×S5上的IIB型超弦理论等价于AdS5边界上的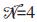 的超对称杨-米尔斯规范场理论。随后,威滕(E. Witten)等猜测:(D+1)维AdS时空中的量子引力理论等价于AdS边界上D维的共形场论[39]。此即所谓的AdS/CFT对应。按照AdS/CFT对应,纯AdS时空对应边界上零温的共形场论,而AdS黑洞对应边界上有限温度的场论,且边界场论的温度就是AdS黑洞的霍金温度。AdS/CFT对应或更为一般的引力/规范场对应为研究量子场论中的一些强耦合问题提供了途径。很多场论中很难实现的计算或原则上无法实现的计算,可以通过引力的计算实现。一个典型的例子即QCD中的禁闭/退禁闭相变可以由前面提到的AdS引力中的霍金-佩吉相变实现。
的超对称杨-米尔斯规范场理论。随后,威滕(E. Witten)等猜测:(D+1)维AdS时空中的量子引力理论等价于AdS边界上D维的共形场论[39]。此即所谓的AdS/CFT对应。按照AdS/CFT对应,纯AdS时空对应边界上零温的共形场论,而AdS黑洞对应边界上有限温度的场论,且边界场论的温度就是AdS黑洞的霍金温度。AdS/CFT对应或更为一般的引力/规范场对应为研究量子场论中的一些强耦合问题提供了途径。很多场论中很难实现的计算或原则上无法实现的计算,可以通过引力的计算实现。一个典型的例子即QCD中的禁闭/退禁闭相变可以由前面提到的AdS引力中的霍金-佩吉相变实现。
引力全息性质是近20年来引力理论和高能物理研究中最引人瞩目的研究对象。它不仅揭示了引力和量子场论之间的深刻联系,更在时空观上改变了人们的认识:至少在一个空间维度上,时空可以呈展出来。这可以说是继牛顿时空观、伽利略时空观、爱因斯坦相对论性时空观之后一次重大的时空观上的突破。当然,完整的新时空观的建立还需要一代代人继续努力。
2.2 引力波引力波在2016年被LIGO组织宣布人类首次直接探测到[15],并在之后发布了一系列引力波事件[40-43]。这标志着引力波天文学步入黄金时期。而我们知道,最早发现的引力波事件GW150914是双黑洞相互绕转合并而发出的引力辐射。因此,精准地描述引力波需要对于黑洞的深入理解。这里简单地介绍霍金的黑洞理论对于理解引力波所带来的帮助。
如前所述,霍金在他博士论文第三部分关于膨胀宇宙的引力辐射中给出了被后人称为霍金质量的引力系统能量定义,它的单调性给出了引力波是否携带能量的准局域解释。此外,在1971年的文章中[16],霍金给出了两个黑洞合并所辐射的引力波能量的上限。而在1979年,霍金和以色列(W. Israel)预测,可以探测到的引力波频率为10-7~1011 Hz[44],基本涵盖了超大质量黑洞双星系统到超新星爆发所发出的引力波的频谱范围。霍金等证明的黑洞无毛定理给出了黑洞最终可由克尔解描述,即描述一个黑洞只需它的质量、角动量和电荷信息。所以,双黑洞系统合并成一个黑洞并发出引力波即可用简单的几个参数描述——黑洞质量、自旋等[45]。这极大地简化了我们用后牛顿近似给出的用来匹配和探测引力波的波形模板。同样,在引力波合并的最后时期——铃宕(ringdown)阶段,准正则模式也需要最后黑洞的质量和自旋估算最后引力波的频率。
3 结论霍金的学术工作为人类留下了宝贵遗产。他在经典和量子引力、宇宙学、黑洞物理等方面贡献是巨大的。他在经典引力中的研究指引着人们走向量子引力,而他在量子引力中的研究为人们进一步揭示引力本质、理解宇宙的创生和演化奠定了基础,点亮了明灯。
谨以此文,缅怀霍金。
注:本文部分内容曾于2018-03-15在“漫步宇宙”微信公众号及腾讯新闻科普频道上发表。
| [1] | Hawking S W. Properties of expanding universes[D]. Cambridge: Cambridge University, 1966. |
| [2] | Bondi H, van der Burg M G J, Metzner A K W. Gravitational waves in general relativity, VII. Waves from axisymmetric isolated systems[J]. Proceedings of the Royal Society A, 1962, 269: 21-52. |
| [3] | Oppenheimer J R, Snyder H. On continued gravitational contraction[J]. Physical Review, 1939, 56: 455-459. |
| [4] | Penrose R. Gravitational collapse and space-time singularities[J]. Physical Review Letters, 1965, 14: 57-59. |
| [5] | Hawking S W, Penrose R. The Singularities of gravitational collapse and cosmology[J]. Proceedings of the Royal Society A, 1970, 314: 529-548. |
| [6] | Ruffini R. Wheeler J A. Introducing the black hole[J]. Physics Today, 1971, 24(1): 30 |
| [7] | Israel W. Events horizons in static vacuum space-times[J].Physical Review D, 1967, 164: 1776-1779. |
| [8] | Israel W. Event horizons in static electrovac space-times[J].Communications in Mathematical Physics, 1968, 8: 245-260. |
| [9] | Carter B. Axisymmetric black hole has only two degrees of freedom[J]. Physical Review Letters, 1971, 26: 331-333. |
| [10] | Hawking S W. Black holes in general relativity[J]. Communications in Mathematical Physics, 1972, 25: 152-166. |
| [11] | Robinson D C. Uniqueness of the Kerr black hole[J]. Physical Review Letters, 1975, 34: 905-906. |
| [12] | Mazur P O. Proof of uniqueness of the Kerr- Newman black hole solution[J]. Journal of Physics A, 1982, 15: 3173-3180. |
| [13] | Bunting G. Proof of the uniqueness conjecture for black holes[D]. Armidale: University of New England, 1983. |
| [14] | Bardeen J M, Carter B, Hawking S W. The four laws of black hole mechanics[J]. Communications in Mathematical Physics, 1973, 31: 161-170. |
| [15] | LIGO Scientific and Virgo Collaborations. Observation of gravitational waves from a binary black hole merger[J]. Physical Review Letters, 2016, 116(6): 061102. |
| [16] | Hawking S W. Gravitational radiation from colliding black holes[J]. Physical Review Letters, 1971, 26: 1344-1346. |
| [17] | Hawking S W, Ellis G F R. The large scale structure of space-time[M]. Cambridge: Cambridge University Press, 1973. |
| [18] | Bekenstein J D. Black holes and entropy[J]. Physical Review D, 1973, 7: 2333-2346. |
| [19] | Hawking S W. Black hole explosions[J]. Nature, 1974, 248: 30-31. |
| [20] | Hawking S W. Particle creation by black holes[J]. Communications in Mathematical Physics, 1975, 43: 199-220. |
| [21] | Gibbons G W, Hawking S W. Action integrals and partition functions in quantum gravity[J]. Physical Review D, 1976, 15: 2752-2756. |
| [22] | Gibbons G W, Hawking S W. Euclidean quantum gravity[M].Singapore: World Scientific, 1993. |
| [23] | Hawking S W, Page D N. Thermodynamics of black holes in anti-De Sitter space[J]. Communications in Mathematical Physics, 1983, 87: 577. |
| [24] |
蔡荣根, 曹利明 . 黑洞的本质[J]. 科学通报, 2016, 61(19): 2083-2092. Cai Ronggen, Cao Liming. The nature of black holes[J]. Chinese Science Bulletin, 2016, 61(19): 2083-2092. |
| [25] | Page D N. Particle emission rates from a black hole: Massless particles from an uncharged, nonrotating hole[J]. Physical Review D, 1976, 13: 198-206. |
| [26] | Page D N. Particle emission rates from a black hole. 2. Massless particles from a rotating hole[J]. Physical Review D, 1976, 14: 3260-3273. |
| [27] | Page D N. Particle emission rates from a black hole. 3. Charged leptons from a nonrotating hole[J]. Physical Review D, 1977, 16: 2402-2411. |
| [28] | Hawking S W, Perry M J, Strominger A. Soft hair on black holes[J]. Physical Review Letters, 2016, 116(23): 231301. |
| [29] | Hartle J B, Hawking S W. Wave function of the universe[J]. Physical Review D, 1983, 28: 2960-2975. |
| [30] | Halliwell J J, Hawking S W. The origin of structure in the universe[J]. Physical Review D, 1985, 31: 1777. |
| [31] | Carr B J, Hawking S W. Black holes in the early Universe[J].Monthly Notices of the Royal Astronomical Society, 1974, 168: 399-415. |
| [32] | Hawking S W. Wormholes in space-time[J]. Physical Review D, 1988, 37: 904-910. |
| [33] | Gibbons G W, Hawking S W, Horowitz G T, et al. Positive mass theorems for black holes[J]. Communications in Mathematical Physics, 1983, 88(3): 295-308. |
| [34] | Hawking S W, Hunter C J, Taylor M. Rotation and the AdS/CFT correspondence[J]. Physical Review D, 1999, 59: 064005. |
| [35] | Chamblin A, Hawking S W, Reall H S. Brane world black holes[J]. Physical Review D, 2000, 61: 065007. |
| [36] | Stephens C R, 't Hooft G, Whiting B F. Black hole evaporation without information loss[J]. Classical and Quantum Gravity, 1994, 11(3): 621. |
| [37] | Susskind L. The world as a hologram[J]. Journal of Mathematical Physics, 1995, 36(11): 6377-6396. |
| [38] | Maldacena J M. The Large N limit of superconformal field theories and supergravity[J]. Advances in Theoretical and Mathematical Physics, 1998, 2: 231-252. |
| [39] | Witten E. Anti-de Sitter space and holography[J]. Advances in Theoretical and Mathematical Physics, 1998, 2: 253-291. |
| [40] | LIGO Scientific and Virgo Collaborations. GW151226: Observation of gravitational waves from a 22-solar-mass binary black hole coalescence[J]. Physical Review Letter, 2016, 116 (24): 241103. |
| [41] | LIGO Scientific and Virgo Collaborations. GW170104: Observation of a 50-Solar-mass binary black hole coalescence at redshift 0.2[J]. Physical Review Letter, 2017, 118(22): 221101. |
| [42] | LIGO Scientific and Virgo Collaborations. GW170814: A three-detector observation of gravitational waves from a binary black hole coalescence[J]. Physical Review Letter, 2017, 119(14): 141101. |
| [43] | LIGO scientific and Virgo collaborations. GW170817: Observation of gravitational waves from a binary neutron star inspiral[J]. Physical Review Letter, 2017, 119(16): 161101. |
| [44] | Hawking S W, Israel W. General relativity: An Einstein centenary survey[M]. Cambridge: Cambridge University Press, 1979: 98. |
| [45] |
蔡荣根, 曹周键, 韩文标. 并和双星系统的引力波理论模型[J]. 科学通报, 2016, 61(14): 1525-1535. Cai Ronggen, Cao Zhoujian, Han Wenbiao. The gravitational wave models for binary compact objects[J]. Chinese Science Bulletin, 2016, 61(14): 1525-1535. |
2. University of Chinese Academy of Sciences, Beijing 100049, China
3. School of Physical Sciences, University of Science and Technology of China, Hefei 230026, China
4. Department of Astronomy, Beijing Normal University, Beijing 100875, China