1946年社会心理学家Heider[1]提出平衡理论用于解释社会成员的想法变化如何影响其他成员,该理论的核心是一个 POX三角的平衡问题。之后,Cartwright等[2]利用图论方法将 Heider的平衡理论推广至社会群组下的演化动力学,讨论了主体在某些特定群体中如何确定自己对其他人的态度。Leik等[3]、Bonacich等[4]、Hummon等[5]也在该方面开展工作,并取得了有意义的结果,特别是2003年Hummon等[6]利用计算机模拟,系统地讨论了群组规模为3、5、7、10的社会平衡问题。以上研究的重点是,探讨个体态度的演变受哪些因素的影响,以及如何将个体态度的变化传递给其他个体。物理学界关注社会平衡问题始于2005年Antal等[7]的工作,他们将POX三角中的边简化成友好敌对,取值用+1和-1表示,在构建的模型中,三角的平衡与否由3条边的乘积决定,乘积为+1,三角形平衡,反之则不平衡;在完全连接网络上研究平衡动力学问题,将社会学中的平衡问题推广到大规模的网络,并研究态度演化的集体效应。近年来,在Antal等工作基础上,人们从统计物理角度出发研究三角动力学相变的普适类[8]、计算机科学中的稳定性等问题[9],除此之外,友好敌对关系对想法传递动力学的影响也得到了关注[10]。大规模网络上的个体态度对社会网络上的传播动力学有深远的影响,因此对社会平衡的研究就显得非常必要。这些开创性的工作,基本都基于完全连接图或规则网络,并取得了很多具有重要意义的结果。例如,Antal等[7]提出了局域和约束两种三角演化动力学,对于局域三角演化动力学,发现网络系统存在动力学相变,该相变由参数转变概率p控制,在临界点概率pc以下,网络系统处于既有友好也有敌对的无序状态,当p≥ pc,网络系统则演化为完全友好的有序态,这些行为与经典自旋系统在复杂网络上的相变有很强的类似之处[11~13];对于约束演化动力学 (网络系统演化与否取决于对网络整体参数的判断),发现网络系统只能存在稳定态和跳跃态,并将其应用于分析国际关系。Radicchi等[8, 9]研究了二维三角网络上的局域平衡动力学,并将三角动力学推广到k-圈动力学,研究了三角网络上相变的临界指数,同时还指出k-圈动力学可以映射到计算机科学中的稳定性问题。Fan等[10]讨论了敌对关系对均匀网络模型传播动力学的影响,分析了传播阈值的复杂性。由于社会网络的复杂性,必然对动力学行为产生影响,Meng[14]研究了二维小世界网络上的社会平衡动力学,并发现该网络系统的自组织临界行为。这些研究揭示了社会平衡动力学的一些重要特点,阐述了该理论的应用前景,但由于研究是基于均匀网络,也没有讨论网络拓扑结构对动力学的影响,不能反映真实社会网络中的平衡动力学特性,因为真实社会网络并不一定是完全连接或是规则连接的,且真实社会网络还应具有演化生长特性。社会网络的这两个特性对平衡动力学产生的影响是一个值得研究的问题。
本文构建一种聚类系数可调节的三角生长网络,以反映社会网络的非完全连接及演化特性,研究基于该网络的局域社会平衡动力学。
1 三角生长网络的构建网络的拓扑结构总是会影响到社会动力学,当动力学过程发生在特定的拓扑结构上,可能会伴随一些非平庸的现象出现[15]。到目前为止,人们提出了很多描述网络拓扑性质的模型,比如小世界网络[16]、无标度网络以及它们的推广模型[17]。这些模型虽然在解释网络中的传播动力学方面取得了很重要的成功,但由于这类模型在稀疏连接时三角结构比例较少,不适于研究三体相互作用下的动力学问题,也不能很好地反映社会网络形成过程中的三角关系。因此,需要构建三角生长网络,以适用于三角动力学的研究,同时反映社会网络生长的三角特性。
构建三角生长网络,参考了Eröds等[16]提出的E-R随机网络和Barabasi等[17]提出的随机生长网络。E-R随机网络是由 N个节点和n条边构成,而这n条边是从N(N-1)/2条可能的边中随机挑选的,网络的聚类系数为

Bollobás[18]推导了该网络的节点度分布,发现在网络规模比较大,即N比较大时,网络的节点度分布满足波松分布。此外,有研究者还讨论了该网络的尺度[19]。对于E-R随机网络,当连接概率p0越大时,网络节点的平均度<k>越大,意味着网络的聚类系数C越大;当p0比较小时,网络的聚类系数较小,此时网络的集团化程度不高,网络中三角形连接的数目非常少。
随机生长网络为无标度网络的特殊情况,该网络在生长过程中保留了无标度网络的生长特性,而将无标度网络的优先连接规则用随机连接规则代替。这样的替换带来的结果是节点度分布为指数型,同时网络的聚类系数较小,网络中的三角连接也比较少。
三角生长网络的构建规则与随机生长网络类似,但为了得到更多的三角连接,引入新的构建规则。
规则1 初始条件:网络由m0个完全连接的点构成。
规则2 新节点的添加:每一个时间步,网络将有1个具有 2条边的节点v被添加。其中1条边随机挑选已存在的节点w连接,剩下的1条边则连接至w最近邻的节点。经过N-m0时间步后,网络将有N个点。
规则3 新边的添加:规则2经历N-m0时间步后,已存在的所有节点以加边概率pa生出2条边,这2条边要寻找连接对象,寻找的方法与规则2相同。
2 三角生长网络的统计性质上述规则2是三角生长网络构建的核心,因为它能保证网络上每增加1个点,都会增加至少1个三角关系。因此,首先研究规则2控制下网络生长N时间步之后的统计性质。聚类系数可以定义为网络中三角连接所占的比例[20]。三角生长网络和随机生长网络的生长时间步数N与聚类系数C的关系如图 1所示。
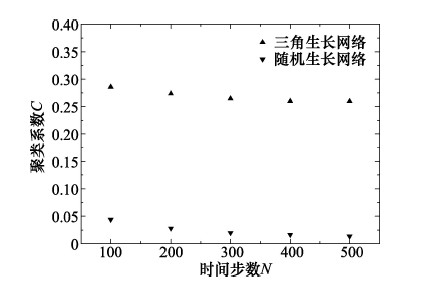 | 图 1 随机生长网络和三角生长网络时间步数与聚类系数的关系 Fig.1 Relationship between the cluster coefficient and time steps of random-growing and triangle-growing networks |
从图 1可以看出,三角生长网络的聚类系数远大于随机生长网络,且三角生长网络含有较多的三角连接,原因是三角生长网络每添加1个点都保证了三角关系的添加,这是由规则2保证的;而随机生长网络每次只保证添加边,而添加边不一定能保证三角关系的建立。
具有500个节点的随机生长网络和三角生长网络的节点度分布如图 2所示。随机生长网络的节点度分布为指数分布,分布函数随节点度的增加呈指数衰减。
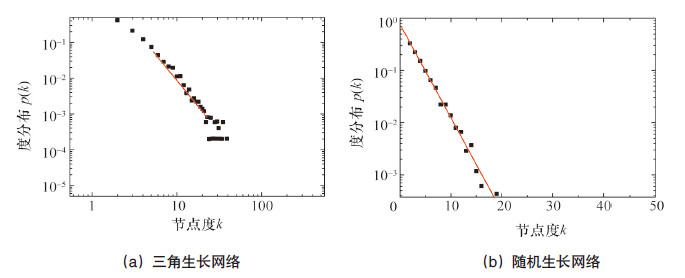 | 图 2 三角生长网络和随机生长网络的节点度分布 Fig.2 Node degree distribution of triangle-growing and random-growing networks |
三角生长网络的节点度分布要复杂一些,如果每个新增加的节点都带有2条边,则任意一个节点w的节点度变化为
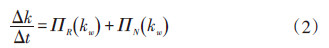
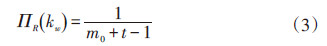
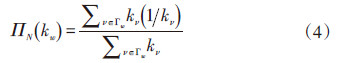
社会网络会不断发展,即使节点个数确定,它们之间的连接也会随时间增加。对于随机生长网络,当网络规模确定后,网络连接的增加是通过随机的方式获得。对于三角生长网络,边的增加则是通过规则3获得,随着边的增加,网络的聚类系数和平均度也是增大的。三角生长网络和随机生长网络的聚类系数随平均度的变化如图 3所示,可以看出,如果平均度比较小时,三角生长网络比随机生长网络大得多,但是随着平均度的增大,两种网络的聚类系数逐渐接近。
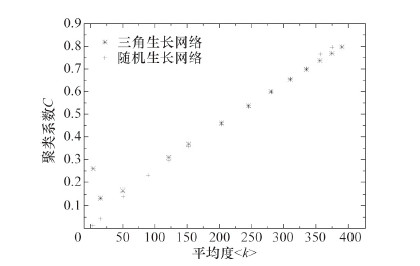 | 图 3 三角生长网络和随机生长网络聚类系数随平均度的变化 Fig.3 Variation of the cluster coefficient of randomgrowing and triangle-growing networks with average degree |
从节点度分布的角度看,当网络的平均度较小时,无标度的特性表明三角生长网络是非均匀的,但如果按照生长规则3,增加网络的边,节点度分布就会发生变化。最极端的结果是,当边加到最多,网络变成完全连接,节点度分布变成δ分布。这说明,网络在生长的过程中,宏观性质发生了根本变化。
3 三角生长网络对社会平衡的影响按照动力学的演化规则,在网络中随机选取1个三角形,若所选三角形是平衡的,不做任何操作,若所选三角形不平衡,网络向平衡演化,此时在三角形中选1个边,使边的值从s变为-s,如果所有的边均为-1,则随机选取1个边改变其值;如果三角中仅有1个边为-1,则以转变概率p将-1变为1,或者将其他2条边中的1条以概率1-p变为-1。
根据Antal等[7]关于完全连接图局域动力学的研究,有限的网络系统最终会处于一个既有友好连接也有敌对连接的平衡态,但当转变概率p≥1/2时,网络系统会达到一个全友好的状态,显示网络系统在该处经历了相变。然而,真实的社会网络未必是完全连接且是演化的,因此本文构建三角生长网络来研究非完全连接网络的社会平衡演化问题,演化规则与前面提到的相同。对于非完全连接网络,是否具有动力学相变,是否能达到稳定平衡,是值得讨论的问题。
为了解决这些问题,需要计算友好连接密度ρ+,即友好连接与所有连接的比值。初始时(即ρ+0=0.5),网络具有相同的友好连接和敌对连接。然后,让网络系统按照局域动力学演化,足够长的时间后网络系统趋于稳定。为了讨论拓扑结构的变化如何影响平衡动力学,通过增加加边概率pa实现网络从稀疏的非均匀网络到完全连接的均匀网络的转变。
稳态时友好连接密度ρ+随转变概率p的变化如图 4所示。可以看出,当加边概率pa比较小时,无论转变概率p多大,网络系统也不可能达到完全友好的乌托邦状态。然而,随着pa的增加,终态的友好连接越来越多,特别是当pa等于或大于一个特定值,即pa≥0.5(通过计算获得),网络系统在p≥1/2时达到了完全友好状态。对于特定大小的网络,由于加边概率越大意味着一个边属于更多的三角关系,网络系统越容易 到达友好状态。另外,一个敌对关系对一个三角形不一定造成非平衡,但是对于另一个三角形可能就是非平衡的,因此网络系统最终的演化结果必然遍及整个网络,从而使友好关系越来越多。
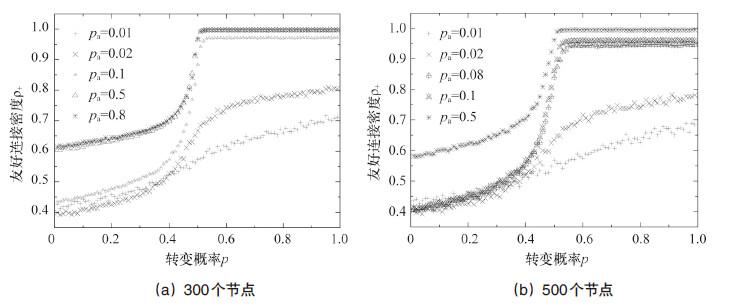 | 图 4 稳态时友好连接密度随转变概率的变化 Fig.4 Density of friendly relations along with the change of transition probability in the stationary sates |
另一个需要关心的问题是三角生长网络的社会平衡动力学演化是否依赖于初始条件。模拟了不同初始条件下2个不同加边概率(pa=0.08,pa=0.5)的网络演化,结果如图 5所示。当pa比较小时,终态显然与初态有关,说明网络系统不能处于稳定的平衡态,外界的扰动会打破稳定,导致网络系统重新演化;当pa比较大时,无论初态如何选取,终态都是相同的。pa=0.08时,不同个体之间的连接非常稀疏,网络有大量相互独立的集团,一个集团动力学的演化很难影响另一个,因此不同的初态将导致不同的终态;当pa≥0.5时,大多数集团之间都是有连接的,一个边的改变将影响网络中大量的集团,这种相互影响使得此时网络系统的终态与初态无关。这一结果说明,即使网络是非完全连接,只要连接足够多,其社会平衡的演化结果与完全连接图类似。
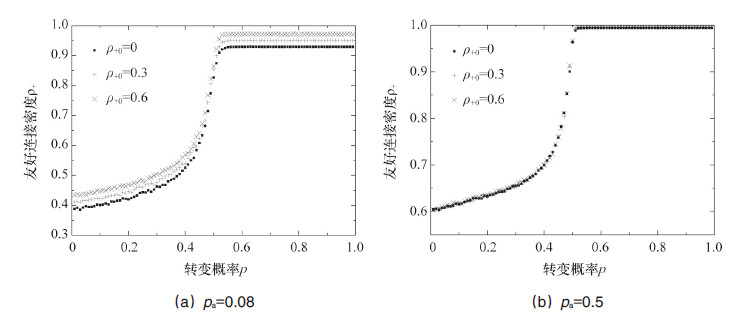 | 图 5 终态时友好连接密度随转变概率的变化 Fig.5 Density of friendly relations along with the change of transition probability in the final sates |
建立一种能够反映社会网络非完全连接与生长特性的三角生长网络,研究了基于该网络的局域社会平衡动力学。发现网络在稀疏连接时,即使构建是随机的,节点度分布也展现出无标度特性,此时,社会平衡动力学的演化依赖于网络系统的初始状态,并且乌托邦式的全友好连接无法实现,网络系统在任何转变概率下都存在一定的敌对连接。但是,当按照边的增加规则增加连接数时,网络系统实现了从非均匀向均匀网络的转变,当连接概率pa≥0.5,社会平衡动力学演化结果与初始状态无关,且在转变概率p≥1/2时网络系统经历从非全友好态到全友好态的动力学相变。
| [1] | Heider A F. Attitudes and cognitive organization[J]. The Journal of Psychology, 1946, 21(1): 107-112. |
| [2] | Cartwright D, Harary F. Structural balance: A generalization of heider's theory[J]. Psychological Review, 1956, 63(5): 277-293. |
| [3] | Leik R K, Meeker B F. Mathematical sociology[M]. New Jersey: Prentice- Hall, 1975. |
| [4] | Bonacich P, Lu P. Introduction to mathematical sociology[M]. New Jersey: Princeton University Press, 2012. |
| [5] | Hummon N P, Fararo T J. The emergence of computational sociology[J]. Journal of Mathematical Sociology 1995, 23(2-3): 79-87. |
| [6] | Hummon N P, Doreian P. Some dynamics of social balance processes: bringing Heider back into balance theory[J]. Social Networks, 2003, 25 (1): 17-49. |
| [7] | Antal T, Krapivsky P L, Redner S. Dynamics of social balance on networks [J]. Physical Review E, 2005, 72(3): 036121. |
| [8] | Radicchi F, Vilone D, Meyer-Ortmanns H. Universality class of triad dynamics on a triangular lattice[J]. Physical Review E, 2007, 75(2): 021118. |
| [9] | Radicchi F, Vilone D, Yoon S, et al. Social balance as a satisfiability problem of computer science[J]. Physical Review E, 2007, 75(2): 026106. |
| [10] | Fan Pengyi, Wang Hui, Li Pei, et al. Analysis of opinion spreading in homogeneous networks with signed relationships[J]. Journal of Statistical Mechanics: Theory and Experiment, 2012, 8(2012): P08003. |
| [11] | 王春阳,孔祥木.长程作用下Gauss系统的临界温度[J].物理学报, 2005, 54(9): 4365-4369. Wang Chunyang, Kong Xiangmu. Critical temperature of the Gauss system under long-range interactions[J]. Acta Physica Sinica, 2005, 54(9): 4365-4369. |
| [12] | Wang Chunyang, Kong Xiangmu. An attempt to introduce long-range interactions into small- world networks[J]. Modern Physics Letters B, 2010, 24(7): 671-679. |
| [13] | 王春阳,孔祥木.二维三角晶格上Gauss自旋模型的临界温度[J].曲阜师范大学学报, 2005, 31(3): 63-65. Wang Chunyang, Kong Xiangmu. Critical temperature of the Gaussian system on a trianglar lattice[J]. Journal of Qufu Normal University, 2005, 31(3): 63-65. |
| [14] | Meng Qingkuan. Self- organized criticality in small- world networks based on the social balance dynamics[J]. Chinese Physics Letters, 2011, 28(11): 118901. |
| [15] | Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamics[J]. Reviews of Modern Physics 2009, 81(2): 591-646. |
| [16] | Barabasi A L. Statistical mechanics of complex networks[J]. Reviews of Modern Physics, 2002, 74(1): 47-97 |
| [17] | Barabasi A L, Albert R. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512. |
| [18] | Bollobas B. [1] Heider A F. Attitudes and cognitive organization[J]. The Journal of Psychology, 1946, 21(1): 107-112. |
| [19] | Chung Fan, Lu Linyuan. The diameter of sparse random graphs[J]. Advances in Applied Mathematics, 2001, 26(4): 257-279. |
| [20] | Wasserman S, Faust K. Social network analysis: methods and applications[M]. Cambridge: Cambridge University, 1994. |