几何与广义相对论——广义相对论一百周年纪念

丘成桐

哈佛大学, 美国波士顿 02138

图1 光线在通过强引力场附近时会发生弯曲，这是广义相对论的重要预言之一

今年是2015年,一百年前,爱因斯坦完成了当时也是以后、到目前为止物理学界一项最伟大的工作,就是广义相对论的创立。广义相对论和牛顿力学加起来,提供了引力场的基础。所有天体的计算和预测,基本上都可以由这两个理论获得。在引力场不是很强的时候,牛顿力学足够计算一切。因此牛顿成为历史上第一个最伟大的物理学家,他有能力来计算很多前人不可能完成的事情。为了完成这些事情,牛顿又发明了微积分,微积分又成为整个物理学、数学和工程的主要分析工具。牛顿能够定量计算天体问题,引人注目。但是到了19世纪,人们发现,牛顿的引力场理论并不是完全正确的。因为在引力场很强的时候,产生很多奇怪的现象,例如重力场会使得光线弯曲,星体过重后会产生黑洞,种种现象非有广义相对论才能解释。

1905年,爱因斯坦开始发展广义相对论,遇到第一个最重要的问题是:牛顿与爱氏对宇宙的看法不一样,即牛顿的宇宙论和爱氏相对论不一样。由于牛顿将时间和空间分开,宇宙是静态的。在广义相对论,这一点完全改变,时间空间不可分,引力场不断地改变时空的几何甚至其柘扑,空间不再是我们看见的三维空间那么简单,三维空间不停地改变,也因此产生了很难理解的引力现象,包括一个很重要的现象--引力波:星球在运行的时候产生引力场的波动现象,这在牛顿力学是不可能解释的事情。广义相对论导致了很多很重要的发现。

到了20世纪,还有另外一个物理学支柱--量子力学出现。量子力学刚开始与引力场关系不大,可是到了20世纪中叶以后,随着科学家对二者的了解加深,量子力学也慢慢地与广义相对论结合。但二者的结合是一个很困难的问题,到现在,广义相对论与量子力学如何结合仍然是最重要最困难的问题。霍金在1970年代初期提出黑洞辐射现象,就是其中一个重要理论。黑洞可以因量子辐射完全消失,到目前为止我们还不知道其真正原因。我们期待量子引力学能够在21世纪完成。其中需要物理学、数学和天文学家们的互相合作才能成功!其中所需要的很多工具要素源于19世纪和20世纪多个重要发现,所以我们要了解历史,由此了解整个现代科学发展的历程,不熟悉历史就不能了解当年这些伟大的科学家是怎么开始这些想法的。这要先由19世纪的发现谈起。

19世纪有很多著名的大数学家,如傅里叶、黎曼、高斯等。有些人的工作我们常常用,但往往我们在用这些工作的时候,忘记了创造这些工作的伟人和他们创造的背景。

傅里叶(图 2)是法国很重要的一位数学家,他颇受拿破仑重视,拿破仑去打仗时,就让傅里叶跟在他的身边。18世纪末19世纪初傅里叶分析的发展,使任何波都可以分解成基本波,而这些基本波有它们的谱,我们在观察粒子和遥远星球的结构时,就要计算这些谱,傅氏理论成为波动和量子力学的主要工具。

图2 傅里叶与傅里叶分析波普

第二个突破是复分析和黎曼面理论的发展。德国数学家黎曼(图 3)通过引入黎曼面给多值函数以几何直观。复分析在波动力学(即量子力学)中有重要作用,因为物质的波函数需要用复数描述。粒子相互作用发生的几率也需要用复数的模的平方来计算。黎曼对空间的定义和曲率的研究,为广义相对论奠定了基础。

图3 黎曼与复分析和黎曼面

群论是法国数学家伽罗华(图 4)的发明。他应用伽罗华群理论,证明五次方程不可解。对称理论的具体化,以及群论特别是李群的发展影响了晶体学,量子力学和高能物理的发展。很多主要的问题都是通过对称的观念来理解的。

图4 伽罗华与群论

在物理学上,19世纪有几个重要的突破,影响到广义相对论的发展。其中最重要的是电学和磁学的融合,这个问题早已引起高斯和黎曼的注意,黎曼甚至推导了3个重要的方程,得出电磁波以光速传播。但黎曼不到40岁就英年早逝,没有见到法拉第(图 5)的著名实验,也没有看到法拉第提出场的概念,电磁学最后在麦克斯韦(图 6)手上才全部完成。

图5 法拉弟

图6 麦克斯韦

麦克斯韦除了发现电磁波以光速传播,更重要的是他发现他创立的麦克斯韦方程组存在着一个对称结构,就是以后叫做罗伦兹(图 7)变换群的结构。此事直接影响了狭义相对论的发展。罗伦兹变换群成为狭义相对论的变换群。

图7 罗伦兹

19世纪中叶可以看到热动力学的理论比较成熟的开始,玻尔兹曼(图 8)和麦克斯韦都是大家,他们对热力学有基本的贡献,最重要的是,玻尔兹曼由此引进熵的观点,对热系统的复杂性提出量的观点,熵的发展到20世纪无论对物理学、数学还是信息学的发展都极度重要。

图8 玻尔兹曼

近30多年来,熵的观念在引力场量子化过程中起着极为重要的作用:贝肯斯坦(Bekenstein)和霍金在1970年代初期建议黑洞的熵正比于它的面积,可以说是引力场量子化的开端。这个建议成为以后霍金量子化的重要的桥头堡。

在19世纪有两个重要的实验,第一个实验是Morley-Michelson的实验(参见图 9),这是一个划时代的重要实验,它证明以太不存在,并且在真空中,光速在任何参照系下都是不变的。这个实验和麦克斯韦方程组在罗伦兹变换下不变这个性质一起成为1905年爱因斯坦建立狭义相对论的基础。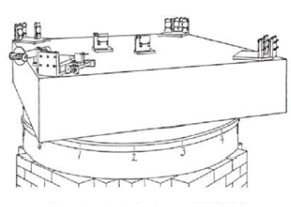

图9 Morley-Michelson 干涉仪

第二个重要的实验是1897年,汤姆逊(Thomson Joseph John,图 10)发现电子,首先证明原子是可分的事实,此前一度认为原子不可分。19世纪的数学和物理学确实为20世纪的伟大科技进展做了极其重要的奠基工作!

图10 汤姆逊

20世纪上半叶的物理学都可以见到爱因斯坦(图 11)重要的贡献,在1905年,他发表了5篇有着划时代重要性的文章。除了狭义相对论外,他解释了一直使人迷茫的布朗运动的原理。也间接地证明了原子理论是正确的。

图11 爱因斯坦

1905年以后,爱因斯坦开始专注于融合狭义相对论和牛顿(图 12)力学的研究。这两个划时代的重要理论有着基本的矛盾。前者认为所有力和信息的传输不能够超过光速,但后者却容许力的瞬间传送。这二者的矛盾必须解决。

图12 牛顿

爱因斯坦在1908年得到重要的启示,他的老师闵可夫斯基(Hermann Minkowski,图 13)将狭义相对论几何化,找到一个以罗伦兹群为等距变换群的黎曼空间,恰巧可以解释狭义相对论的一切现象。

图13 闵可夫斯基

但是空间加上时间变成四维时空(图 14),时间和空间不再可以分割。这个漂亮的解释让爱因斯坦认为是对他一生最重要的启示。他发现新的引力理论不可能单从牛顿力学加上狭义相对论就可以完成。因为在牛顿力学,引力场只用一个标量就可以解释,但是由Minkowski时空做出发点,需要用到张量。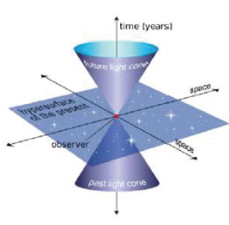

图14 四维时空

张量的概念产生于19世纪末,由克里斯托费尔(Christoffel Elwin Bruno,图 15)提出。刚开始时,爱因斯坦不知道他确切需要的是什么,但他知道他需要的量在空间每一点上和方向有关,直到他问他的大学同学格罗斯曼(Mar-cel Grossmann,图 16)时才知道张量这个观点。为什么他需要的量和方向有关?因为在狭义相对论里,物体在运动的方向,长度会跟着速度收缩或增加,而和速度垂直的方向,却没有变化。爱因斯坦做了很多思想实验来得到这个结论。

图15 克里斯托费尔

图16 格罗斯曼

这个张量其实是黎曼几何里的黎曼张量,爱因斯坦要用它来描述引力场,如何找到和牛顿场方程类似的方程是一个主要的问题。在找寻这个方程时,爱因斯坦要用到一个很重要的对称原理叫做等效原理,就是说这个引力方程无论用什么坐标去描述都有同样的结果。这个原理在伽利略时代已经开始讨论,而且实验也得到证实。有了这个原理后,我们推广牛顿方程,这个方程用一个Poisson方程来描述,左边由Laplace算子作用在引力场来表示,右边是物质分布的密度。由于爱因斯坦的方程在引力不是很强的时候,需要还原到牛顿方程。和牛顿力学比较后,爱因斯坦发现方程一边需要由引力张量表示,另外一边则需要是物质张量。我们要找到广义相对论中这两个场怎样描述,引力场的势能由一个黎曼度量来描述,物质场应当是引力场的微分得出。(如果不是微分,场方程不再是局部方程,会产生奇怪的现象。)从牛顿方程看,最自然的是二次微分。我们的结论是物质张量是引力张量的二次微分得出来的,由于等效原理,它必须是个张量。

爱因斯坦坚持让Grossmann帮忙去寻找从一个黎曼张量通过二次微分得到新的张量的可能性。最后Gross-man在图书馆找到了这个张量:在19世纪时意大利几何学家Ricci (图 17)发现了一个后来以他的名字命名的张量叫做Ricci张量,它是黎曼曲率张量的二次缩并得出來的张量。于是爱因斯坦和Grossmann在1912年和1913年写下两篇文章。这两篇文章在广义相对论中具有重要的意义,因为它第一次发现引力场用张量描述,但这个发现还是有一些问题。爱因斯坦无法用这些文章的结果来解释水星近日点进动和牛顿方程预言的偏差问题(图 18),所以他知道这个方程还是没有成功。他几乎放弃等效原则来补救对物理观测的解释,这种做法使他愈走愈远。这是一个很有趣的事情。

图17 Ricci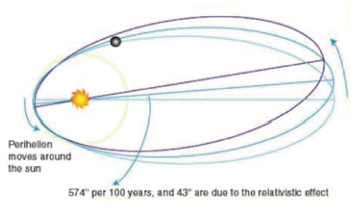

图18 水星进动与牛顿方程预言的偏差

所以在他以后的文章中,爱因斯坦虽然极度重视物理观测,但是他也同意:由数学产生出来的美丽而又足以描述大自然的理论有同样的重要性。伟大的数学物理学家Weyl (图 19)甚至说,在实验和数学的美两者之间,假如他非要做选择的话,他宁愿选择优雅的数学。

图19 Weyl

在1914-1915年间,爱因斯坦不停地找几何学家帮忙,其中著名的有Levi-Civita (图 20)和Hilbert (图 21),都是名家。尤其是他和Hilbert的讨论对广义相对论的贡献极度重要。事实上,Hilbert在1915年11月20日,比爱因斯坦还要早5天在Gottingen科学院宣布他找到引力场方程,并找到推导方程的拉格朗日算子a lagrangian。(爱因斯坦听到这个事情后,在11月25日于柏林宣布他的结果。)这事引起爱因斯坦的不满,但是爱因斯坦熟悉这个场方程的物理意义,用它来解释了一直悬而未决的水星进动角问题。所以Hilbert也认为应当叫这个方程为爱因斯坦方程。其实这个方程就是上述的Ricci张量减去它的迹乘以1/2的度规张量。为什么要加这个项?因为只有这样,方程才能够满足物质守恒律,而且这个定律可以由Ricci理论的一个恒等式推导出来。

图20 Levi-Civita

图21 Hilbert

几年后爱因斯坦为了建立一个静态的宇宙学模型,就修正他的方程;在左边加上一个常数乘上引力张量,这个常数叫做宇宙学常数。当1929年天文学家Hubble (图 22)用望远镜发现宇宙的确在不断膨胀时,爱因斯坦说他一生最不应当做的事，就是引进了这个常数。

图22 Hubble

这是历史上一个很有趣的事情,直到20世纪80年代,一般物理学家认为宇宙常数必须是零,同时宣称这是人类观察自然界得到的最准确的数据。但是在20世纪90年代发现暗能量的现象,有很多物理学家认为用非零的宇宙常数可以解释暗能量。无论如何,宇宙常数是否是零仍旧是一个重要问题。

至于Hilbert引进的作用量原理(Action Principle),在这一百年来无论在经典广义相对论还是引力量子化都起着同场方程一样重要的作用。

另外一方面,爱因斯坦以为他的场方程可以用来决定引力场的一切,但这并不正确。因为给定方程,需要解决初始值和边界问题,才能决定它的解的变化。宇宙学家到现在还在争论宇宙起源的初始值如何决定,大家都想从引力量子化来解决这个困难问题,并做了重要的工作。

但是无论如何,在1916年,Schwar-zschild (图 23)就找到爱因斯坦场方程一个球对称的解。这个解很重要,可以用来计算星球的光线受到太阳重力场改变方向的角度,在1918年由英国天文学家Eddington (图 24)在南非和巴西的团队观察到它的正确性。由《纽约时报》刊登后,爱因斯坦成为全世界妇孺皆知的名字。同样的计算在最近十年也用于全球定位系统,可见广义相对论的威力。

图23 Schwarzschild

图24 Eddington

不过上文说的边值的问题始终未全部得到了解,它和黑洞问题有关,这些都是很困难的问题,因为引力场方程是一组极其复杂的非线性方程组,往往产生意想不到的效应。爱因斯坦喜爱他的方程,很想用它来推导其他物理现象,他希望完成物理学所有力场融合起来的理论,所以很多物理学家和数学家朝这个方向走。

引力场要求时空是弯曲的，主要的原因是爱因斯坦方程是非线性的。一般的时空,不再存在任何对称,因此所有牛顿力学中常用的守恒量不再存在。如何找到它们在广义相对论的位置?这个问题在爱因斯坦时已经提出,它的物理意义极为重要。举例来说,时空的总能量是否为正是一个极为重要的问题,因为它是负的话,时空会变得不稳定,广义相对论不再是一个好的物理理论。这个问题困扰物理学家半个世纪之久,终于在1976年由Schoen和我解决。除了总能量外,另外一个重要问题乃是局部能量的定义和性质的问题,最近由王慕道和我解决,陈柏宁也参与,并做了重要的工作。

在爱因斯坦伟大的发现后,跟着有两个很重要的发展。首先是数学家Kaluza (图 25)提出五维时空的真空场方程在圆为对称群作用下可以推导出四维空间上引力场和电磁场的方程,这个理论由物理学家Klein加强,很得爱因斯坦欣赏,直到如今,弦论学家还是喜欢这个理论,只不过圆周由Calabi-Yau空间代替。

图25 Kaluza

第二个重要的发展是Weyl引进了规范场论,通过10年努力,解释了电磁场可以描述为规范场,这是划时代的贡献。30年后杨振宁和Mills (图 26)推广了Weyl的理论,物理学上的弱作用和强力作用都需要规范场来解释。

图26 Yang and Mills

19世纪末叶和20世纪初期发现的放射性物质对基本物理有极度重要的影响,对黑体辐射的研究最后引出了量子力学。量子力学的伟大贡献者,除了爱因斯坦外,早期的有Bohr,Planck (图 27),Sommerfield,Heisenberg,Dirac,Schrodinger,Pauli,Fermi,Born,Bose,Wigner,Yukawa等人,后期发展的量子场论重要贡献者有Feynman,Schwing-er,Tomonaga,Dyson,Gell-Mann,Lee,Yang等人。

图27 Planck

之后规范场的量子化,需要丰富的几何和场论知识,由荷兰物理学家Ge-rard't Hooft首先完成,他用到Feyn-man、Faddeev、Popov、DeWitt等人的准备工作。以后Veltman、Salam、Wein-berg、Glashow、Gross、Wilczek、Politzer等人更在这些基础上完成了现代粒子物理的Standard Model,解释了几乎所有基本粒子的现象。这是人类文明的极致。谁能想到我们在纸上做一些计算,在实验室就可以找出准确到小数后十位数字的实验测量!这是一百年来物理学家和数学家辛勤工作而累积起来的伟大成果。

广义相对论处理大尺度的时空极为有效,但是在尺度极度微小的空间,它还是有问题的。因为它假定空间是连续的,但是在量子力学里,在尺度小于Planck的尺度以下,一般连续空间的定律不再成立,而必须要由量子力学的定律代替。从大到小怎样完成,这是理论物理上最重要的问题。

物理学上,我们已知的力有电磁力、弱力、强力、引力。前面3个力,经过物理学家数十年的努力,完成了标准模型,已经成功地融合成为一体,并在实验上得到验证。但是引力的尺度和前面3个力场的尺度格格不相入,如何将它们融合,是爱因斯坦梦寐以求的事情,也是理论物理最基本的问题,和前面说的大小尺度的问题有密切关系。

引力场如何量子化在这30年来成为极为重要的题目,在1984年人们开始注意弦论的发展,弦论假定基本粒子间存在一种对称性,叫做超对称,它将费米粒子和玻色粒子一一对应。在这个假定下,弦论假定粒子可以由弦线代替,它在空间的振动,产生了粒子的现象。弦论在这些假定下,成功地将引力场量子化。不过它要求时空是十维的,弦论学家用了上述的Kaluza-Klein的理论。他们假定十维的时空可以写成四维时空和一个很小的六维空间乘积。这个六维空间重要的模型是Cala-bi-Yau空间(图 28)。从空间的几何可以计算宇宙粒子的基本性质。虽然弦学的理论解决了不少问题,但是在实验室,还是没有找到超对称,所以还是没有定论。

图28 卡拉比-丘(Calabi-Yau)空间

但是超对称的观念和弦学产生的数学想法在近30年的数学领域产生了深远的影响,它们帮助数学家解决了很多悬而未决的问题,也开启了新的方向。举个例子,Calabi-Yau空间的理论虽然由我在1976年用数学方法完成,也在数学领域里解决了很多重要的问题。但是直到1984年弦论开始在物理学流行以后,才在数学以外的学科大为流行。而且奇妙地将数学很多重要的分支结合在一起,得到很大的进展。弦论兴起以后,引力场的量子化成为一个很热门的学问。最重要的发展都跟黑洞理论有关。黑洞很早就出现在Schwarzchild对爱氏方程的解上。但要到近30年天文学家才全面接受这个理论。其实在20世纪60年代Penrose和Hawking已经从数学的观点解释黑洞的必然性。与此同时,Kerr发现了爱氏方程的一个带角动量的轴对称解。这个解成为以后黑洞研究的主要模型。Carter等人更证明黑洞在稳定的状态下,由Kerr解来描述。在引力场量子化理论里,这是一个极为重要的事情。

大量的物质在重力场作用下塌陷成为黑洞(这个事实,由我和Schoen在1983年在数学上严格证明。)从量子力学的观点来说,这是很奇怪的现象:因为Kerr黑洞很简单,这表示宇宙间很多复杂的讯息一下子不见了。这个现象违反了量子力学的规则。因此引起了激烈的辩论。

在1970年代初,Bekenstein和Hawking引进热力学第二原理,在引力理论里引进了熵的概念,并写下熵的方程。这是量子引力理论的开始,因为Hawking从这里提出他的黑洞辐射理论。但是要到1990年代初期,熵的公式才由Strominger和Vafa从弦理论的基本结果推出。Hawking也因此对弦论改变他原先反对的立场。

黑洞是引力场极度强烈时出现的现象,因此也是量子力学和古典引力场交汇的地方。它的研究在这30年的理论物理起着关键性的影响。其中一个是Maldacena提出的AdS/CFT理论。他提出量子引力场论和在边界上的量子规范场论等价。这是极为重要的理论,它影响了近15年来理论物理的发展,这也是爱因斯坦喜欢的理论。引力理论对其他力场的影响愈来愈重要。上述这些理论,无论是广义相对论也好,标准模型也好,假如没有良好的天文观测和实验,可能都是纸上谈兵。一个理论,没有预测的能力,很快就会令人厌倦,而提不起精神继续开展新的方向,这一点是物理学能够帮助数学发展的重要原因。

反过来说,物理学发展出来的理论,有时无法达到足够高的能量去做实验,这时可以检查这个理论在数学上的预测结果如何。假如预测的结果极为美妙,而且数学家从前没有想过,而且可以给予严格的证明时,我们对这些物理理论会更具信心。

作者简介：哈佛大学数学教授、物理学教授，美国科学院院士，中国科学院外籍院士，电子信箱：yau@math.harvard.edu

（责任编辑 李娜）