在科学史上，恐怕没有哪一个理论会像相对论这样，引发那么多的 “佯谬”，双生子佯谬是其中最著名的一个。

根据狭义相对论，对静止的观测者来说，运动物体的时钟会变慢。而相对论又认为运动是相对的。那么，有人就感到糊涂了：站在地面上的人认为火车上的人的钟更慢，坐在火车上的人认为地面上的人的钟更慢，到底是谁的钟快、谁的钟慢？人们（包括物理学家）总想不通，于是，便总结出来了一个 “双生子佯谬”。这个概念，最早是由物理学家朗之万在1911年提出的。

假设在1997年的某一天，诞生了一对双胞胎，其中哥哥（刘天）被抱到宇宙飞船1号送上太空； 弟弟（刘地）则留守地球过普通人的日子。

飞船1号以极快的速度（光速的3/4）飞离地球（图1中向右）。根据相对论的计算结果，在如此高的速度下，时间变慢的效应很明显，大概是3:2左右。所谓 “时钟变慢”，是一种物理效应，不仅仅是时钟，而是所有与时间有关的过程，诸如植物生长、细胞分裂、原子震荡，还有心跳，所有的过程都放慢了脚步。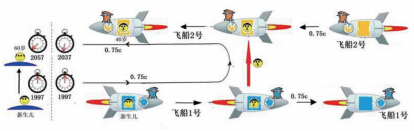

图1 双生子佯谬解释模型

总而言之，当自认为处于 “静止” 参考系中的人过了3年时，他认为运动的人只过了2年。按照地球人的计划，1997年发射的宇宙飞船1号，将于地球上30年（而飞船1号上20年）之后，在某处与飞船2号相遇。飞船2号是朝地球飞过来的（图1中向左），速度也是光速的3/4左右。在那个时刻，刘天从飞船1号转移到飞船2号上。

由此，地球上总共经过了60年之后，2057年，一对双胞胎终于能够再见面了。那时候，刘地已经60岁了，但一直生活在高速运动的飞船中的哥哥刘天却只过了40个年头。

不过，有人便说：刘天会怎么想呢？爱因斯坦的狭义相对论不是说所有的参考系都是同等的吗？刘天在两艘飞船中不也一直是静止的吗？地球上的弟弟却总是相对于他作高速运动，因此，他以为弟弟应该比他年轻许多才对。但是，事实却不是这样，他看到的弟弟已经是两鬓斑白、老态初现，这便似乎构成了佯谬。我们应该如何解释刘天心中的疑惑呢？
佯谬不成立

首先，刘天有关狭义相对论的说法是错误的。狭义相对论并不认为所有的参考系都等同，而是认为只是互相作匀速运动的惯性参考系才是等同的。刘天在旅行过程中坐了两个宇宙飞船，他的旅程分成了飞离地球（飞船1）和飞向地球（飞船2）这两个阶段。飞船1和飞船2可以分别当作与地球等同的惯性参考系，但刘天的整个旅行过程却不能作为一个统一的惯性参考系。

因为刘天的观察系统不是惯性参考系，刘天便不能以此而得出刘地比他年轻的结论。所以，“佯谬” 不成立。当刘天返回地球时，的确会发现地球上的弟弟已经比自己老了20岁。如果设想两个宇宙飞船的速度更快一些，接近光速，当刘天返回地球时，的确就可能出现神话故事中描述的 “山中方一日，世上已千年” 的奇迹了。
“时间变慢” 的相对性

首先，我们用两维的时间空间图，研究双生子佯谬中时间变慢的相对性。

图2中有两套时空坐标：地面上刘地使用的(x,t)以及飞船1上刘天使用的(x’ ,t’ )。（注意：刘天在飞船1上只待了一半，后来转到飞船2，而图中并没有画出飞船2上的坐标系。）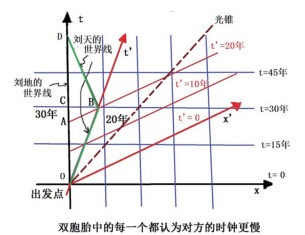

图2 地球惯性系（黑色直角坐标）和飞船1惯性系（红色斜交坐标）中同时的相对性

两个双生子的时空过程，可以分别用他们的 “世界线” 来表示。世界线是某个事件在时空中所走的路径。用这个新名词，以区别于仅仅是空间的 “轨迹” 或者仅仅时间的流逝。比如，刘地在地球上一直没有动，所以他的世界线是沿着地球坐标系的t轴，为O－A－C－D，在图2中是一条垂直向上的直线。而刘天坐了两次宇宙飞船，他的世界线在图中是O－B－D的一条折线。

对地球参考系而言，同时的点位于平行于x轴的同一条水平线上，即水平线是同时线。比如说，地球上2012年发生的事件都在标志了 “t=15年” 的那条黑色水平线上。

飞船1号的时空坐标相对于地球时空坐标来说有一个旋转，如图中红色的斜线所表示。但这儿的所谓 “坐标轴旋转”，不同于普通空间中的旋转，被称为 “双曲旋转”。对于普通空间中的坐标转动而言，直角坐标转动后仍然是直角坐标。但在时空中，坐标变换时需要保持光速不变，也就是保持光锥的位置总是在黑色坐标系的45°处，如图2中的虚线所示。所以，当时间轴顺时针转动时，空间轴需要逆时针转动，以对光锥保持对称。

现在，我们只研究刘地30岁之前的情况，即他的世界线从O到C的一段。

对飞船1号的时空参考系而言，等时线不再是水平线，而是平行于x'，即t' =0、t' =10年、t' =20年的那些红色斜线。例如，研究一下图2中的A、B、C这3个事件之间的关系。在地球的时空坐标中，C和B是同时的，都发生在地球时间t＝30年的那条等时线上。然而，从飞船1的时空参考系看来，A和B才是同时发生的，都发生在飞船1的时间t’ =20年的那条等时线上。而飞船1看起来，C事件是在A事件之后，所以也在B事件之后。

现在，刘地使用的是地球坐标系，他认为C和B是同时发生的，C点在刘地的世界线上，表明刘地30岁； B点在刘天的世界线上，表明刘天的 “地球年龄” 也是30岁。但因为刘天实际上是在运动的飞船1号上，所以刘地认为刘天的时间过程要过得更慢，因而，刘地认为刘天的 “真实年龄” 是20岁。

到地球上的2027年为止，刘天（B点之前）一直都在飞船1号上。在他看来，B点对应于自己20岁，与B同时的是A点，弟弟刘地相对于 “我” 是运动的，时间应该更慢，所以，在刘天看来，自己在B点是20岁，而A点的刘地还不到20岁。

到此为止，两个人的说法都是正确的，每一个人都认为对方坐标系中的时钟（还有衰老的过程）比自己的更慢，从而都可以得出对方比自己更年轻的结论。
地球和飞船 “转换”

对两个互作匀速运动的惯性参考系而言，每一个观测者都认为对方的时钟更慢，都认为对方比自己更年轻。这个结论对地球和飞船1（刘地的前30年）是如此，对地球和飞船2（刘地的后30年）也是如此。

但是，想象一下，如果刘天只坐在飞船1上的话，他和刘地相距只会越来越远，就永远不可能再见面了，因而也就不可能构成前面所述的 “佯谬” 之说。即使他们互相都认为对方更年轻，但却无法验证对错。不过，有人可能会说：他们虽然不能见面，但是可以通电话呀，在电话中他们互相一问，不就知道对方多少岁了么？然而，狭义相对论认为信息的速度不可能超过光速，当他们以光速通话时，也需要考虑他们之间的距离以及同时性等等问题。因此，对这种通电话的情况，就不进一步详细分析了。

关键在于，刘天不是一直待在匀速运动的飞船1上，也不是一直待在反方向匀速运动的飞船2上，而是在半途从飞船1瞬间被转移到了飞船2，掉头（从+0.75c的速度，变成-0.75c的速度）向地球飞来。最后两兄弟相遇时，刘天比刘地年轻，其秘诀就隐藏在刘天的旅程中包括了这段从飞船1到飞船2的 “转换” 过程。

那么，既然在双生子佯谬中需要考虑刘天在两艘宇宙飞船中切换的加速度，是不是需要广义相对论的知识才能解释清楚它呢？也不是这样的。用地球参考系的二维时空图就可以解释，用 “固有时” 的概念，还可以计算刘天相对于刘地的年龄。
用固有时计算

固有时也称原时，其数学意义是二维时空图中的一段 “长度”，类似于普通空间中的弧长s。具体来说，刘天和刘地的年龄，可以用图2中他们世界线的弧长来计算。

在图2中的地球坐标系中，两个双生子的世界线都是从O到D，这是标志他们交汇见面的两个时空点：分别对应于他们出生之时（O）和地球上60年之后（D）。刘地的世界线是直线OD，等于线段OC的两倍。刘天的是折线OB+BD，等于线段OB的两倍。读者可能会认为：图中直角三角形的斜边OB “看起来” 不是比直角边OC要长吗？这点在普通空间是正确的，在 “时空” 中却未必见得。这是因为时空中线段OB的长度的平方是等于OC（时间）的平方减去CB（空间坐标值）的平方。

在普通空间中，弧长s表示一条曲线的长度，或者说是一个人走过路径的长度。而固有时表示的是某种时间。如图3a，设想一个旅行者（太空人），带着自己的时钟和卷尺，一直记录他走过的时间和距离，而时钟所记录的，就是固有时。

从图3b可以看出固有时和坐标时（间）的区别，坐标时是事件之外的观察者使用某个参考系记录的事件发生的时间间隔，固有时则是旅行者自己携带的时钟记录的时间间隔。此外，固有时与弧长不同之处是：普通空间的弧长一般比坐标数值更大，但固有时却比坐标时更小，其原因如刚才所举的例子中描述过的，是因为空间坐标平方和时间坐标平方间的符号差所致。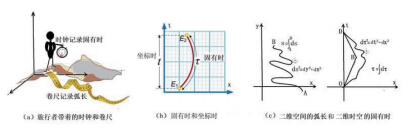

图3 固有时和坐标时的区别以及与弧长的类比

换言之，固有时用以描述时空中事件之间流过的时间，这个时间被事件自身的时钟所测量，测量结果不仅取决于两个事件对应的时空点位置，而且也取决于时钟参与其中的具体过程。或简单地说，固有时是时钟自己经过的世界线长度。

如何来计算双胞胎在重逢时各自度过的真实年龄呢？可以计算和比较他们在两次相遇之间，每个人的世界线长度。每个人的年龄是由身体的新陈代谢机制决定的，身体内有一个生物钟。人体处于各种运动状态（静止或运动、加速或减速）时，他的生物钟便会随着变化，这便可以作为每个人自己带着的 “时钟”。

刘地一直停留在地球上没有移动，他的世界线是地球参考系中时间轴上的一段直线，在这个参考系中，他的固有时也就等于坐标时，等于60年。而刘天的世界线是图2中的OBD折线。折线中每一段的长度是20年，两段相加等于40年。所以，两个双生子在D点见面的时候，刘天40岁、刘地60岁。

从以上分析可以体会到利用 “固有时” 来计算此类问题的方便之处。我们并不需要仔细考虑每个事件的过程，不需要详细去分析刘天的旅行过程哪一段是匀速、哪一段是加速或减速等等繁琐的细节，比如图3c右图中的从O到D的弯弯曲曲的曲线，如果那是刘天的时空轨迹的话，也只需要在地球参考系中使用积分计算出这条世界线的长度（即固有时），那便就是刘天的年龄了。

这样的分析是基于地球坐标系，事实上，使用飞船1号的参考系，或者飞船2号的参考系，也都可以验证以上结果。3种情形可得到同样的结果：刘天40岁、刘地60岁。

（原标题：著名的双生子佯谬到底几个意思）

文/张天蓉
作者简介 美国德克萨斯州大学奥斯汀学校， 理论物理学博士。
（责任编辑  王丽娜）