2. 中国科学院机器人与智能制造创新研究院, 辽宁 沈阳 110169;
3. 中国科学院大学, 北京 100049;
4. 燕山大学机械工程学院, 河北 秦皇岛 066004
2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China;
4. Yanshan University, School of Mechanical Engineering, Qinhuangdao 066004, China
至2030年,我国将有超过3 000万脑卒中患者,各类残疾患者的总数将超过8 000万人[1-2]。下肢康复外骨骼[3-6]作为服务于下肢伤残及运动障碍患者的辅助康复设备,能够完成更高精度的重复性康复训练,相比于固定康复设备能显著提高患者的能动性。
近十年来国内外多个研究团队进行了下肢康复外骨骼的研究。Kwa等[7]设计了IHMC-MAE(IHMC mobility assist exoskeleton)系统,该系统具有多个主被动自由度以适应下肢关节运动,以健康人群步态数据为参考轨迹,牵引穿戴者复现步行运动。Sankai [8]设计了HAL(hybrid assistive limb)外骨骼康复系统,利用肌电信号对关节力矩进行估计,并结合阻抗模型计算人机交互关节的输出力矩,从而帮助偏瘫患者完成康复运动训练。以色列ReWalk公司研制了ReWalk系列外骨骼[9],该外骨骼能够检测穿戴者的运动重心变化,进而模拟自然步态运动并防止在运动过程中发生意外跌倒。中国科学院合肥智能机械研究所、哈尔滨工业大学、中国科学院深圳先进技术研究院、中国科学院沈阳自动化研究所[10]等科研院所也开展了相关研究,并设计了一系列实验样机。尽管围绕下肢康复外骨骼的研究很多,但其应用的可行性仍不显著,原因在于刚性外骨骼在结构设计和人机交互方面均存在技术难点,具体表现在以下两方面:
(1) 在结构设计方面,刚性外骨骼以人体下肢骨骼为构形,当刚性连杆与关节位置未对齐时将产生非期望交互力矩,从而严重影响系统控制性能。
(2) 在人机交互方面,外骨骼的刚性远大于人体下肢,系统柔顺性决定了穿戴者的舒适性和康复治疗效率。除硬件系统的柔顺设计外,也要求控制算法能实现步态的准确识别和参考轨迹的准确追踪。同时应综合考虑外骨骼驱动力矩的约束或输出约束,确保交互过程的安全性与舒适性。
模块化、柔顺性的外骨骼关节可有效解决上述问题,原因在于:1) 模块化关节能够优化连杆—关节配置方案,改善结构设计的灵活性,提高系统功率密度,降低总重量与末端惯量;2) 对刚性系统引入柔顺性结构从而降低系统机械阻抗,缓冲瞬时过载冲击,提高交互柔顺性与安全性。
串联弹性驱动器(SEA)是柔顺性模块化关节的重要设计内容。该概念最早由Pratt等[11]在1995年提出,即在刚性传动机构中引入弹性环节。相比于传统刚性驱动器,SEA能够改善系统柔顺性,具有低阻抗、抗冲击、力控稳定等特点,但对控制算法设计提出了更高的要求。Pratt等率先提出应用于SEA的比例—积分—微分(PID)力矩控制算法,Tagliamonte等[12]在此基础上引入了级联PD以优化系统柔顺性。为提升控制算法的鲁棒性,Kong等[13]提出了基于线性扰动观测器的控制方法,Calanca等[14]设计了基于参考模型的自适应控制方法。前述研究对象均为SEA线性系统,而实际系统存在非线性环节。为此,朱秋国等[15]利用反向传播(BP)神经网络补偿负载重力,王萌等[16]先后利用有限时间输出反馈控制、鲁棒误差积分最优控制、有限冲击响应滤波等方法对非线性SEA进行力矩控制和抖动抑制。
在康复机器人领域中,不仅需要对SEA模块进行控制,还需要考虑系统集成问题和人机交互设计[17]。在系统集成问题上,SEA应兼顾临床应用需求与结构的小型化、轻量化、低惯量;在交互过程中应确保安全性和舒适性[18]。Gerlach-Hahn等[19]设计了集成SEA的膝关节康复外骨骼,并应用了级联PD反馈控制,但其SEA体积较大,需要额外的弹性元件固定器件。Kim等[20]针对下肢外骨骼的非线性SEA系统采用了一种基于逆向模型的控制方法,但未处理输入饱和导致的控制抖动。
综上所述,上述研究中设计的SEA弹性元件难以实现小型化与轻量化,在控制算法上缺少控制量的约束设计,仅以输入饱和限制控制量可能引发系统抖动甚至系统发散。因此,本文设计了一种应用于下肢康复外骨骼的串联弹性关节,并提出了迭代线性化模型预测控制方法,主要创新工作在于:
(1) 设计了面向康复外骨骼的串联弹性关节,该关节具有结构紧凑、质量较轻、承载能力大的特点,在优化系统柔顺性的同时,能够根据外部载荷实现线性/非线性刚度的切换。
(2) 针对串联弹性关节研究了带约束非线性优化问题,提出基于模型预测控制的迭代线性化方法,结合Laguerre网络优化求解非凸优化控制问题。通过对系统控制量的约束,避免了控制量出现尖峰和抖动,改善了人机交互过程的舒适性。
2 串联弹性关节设计(Design of the series elastic joint)康复外骨骼需要与穿戴者进行深度的人机交互,因此对关节轻量化与紧凑化要求较高。现有的康复外骨骼倾向于在关节处集中布置驱动元件,导致关节轴向尺寸较大而连杆空间未能有效利用。基于此设计了一种具有多分支弹性单元的串联弹性关节。
2.1 多分支弹性单元结构设计通常情况下,标准的SEA需要包含弹性元件以串联驱动电机实现运动传递,因此弹性元件是SEA设计的主要对象。本文基于多分支平面涡卷扭簧提出了一种新型弹性单元,该弹性单元由多个不接触的涡卷弹簧并联组成,如图 1所示。

|
图 1 多分支涡卷扭簧 Fig.1 Multi-branch scroll torsion spring |
基于并联的结构配置,多分支涡卷扭簧能够实现结构的紧凑化与轻量化,从而能在关节有限的空间内作为SEA的弹性元件。扭簧在预紧装配后呈现阿基米德螺旋线(涡状线)形状,两端固定于SEA金属结构的内外轮。加载外力后,内外轮发生相对转动并将载荷传递至涡卷扭簧,导致涡卷扭簧发生弹性形变:
| $ \rho =\alpha +\beta \cdot \theta $ | (1) |
其中,
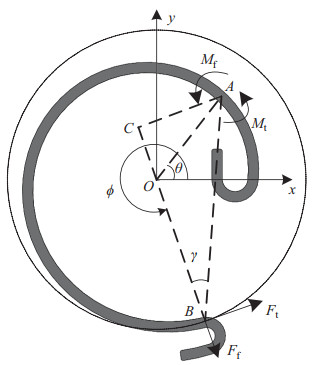
扭簧的弯曲变形主要由扭簧横截面所受弯矩引起,弹性体受力分析如图 2所示。其中,
|
图 2 涡卷扭簧弹性体受力分析图 Fig.2 Force analysis on elastomer of scroll torsion spring |
任取弹簧形变部分内任一点
| $ M_{\rm t} =[(\alpha +\beta \theta)\cos (\phi -\pi -\theta)+\alpha +\beta \theta]F_{\rm t} \\ M_{\rm f} =\mu (\alpha +\beta \theta)\sin (\phi -\pi -\theta)F_{\rm t} $ |
弹簧外端点
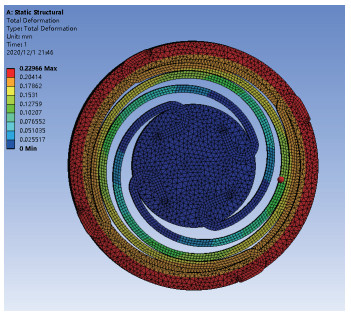
为实现刚度计算,基于Ansys-WorkBench有限元分析软件对多分支涡卷扭簧进行了仿真试验[21]。仿真模型包括弹簧内外轮及弹簧弹性体,接触部分添加绑定接触。仿真过程中在对内轮施加固定约束的同时对外轮施加等效力矩。假设弹簧受力矩
| $ k =\frac{M_{{\text{ext}}}} {\theta_{\rm s}}, \quad \theta_{\rm s} =\arcsin \frac{d}{2R} $ |
Ansys-WorkBench软件中扭簧的位移结果如图 3所示。由前述计算得到的弹簧刚度为60 N
|
图 3 弹簧刚度有限元分析 Fig.3 Finite element analysis of spring stiffness |
为验证四分支平面涡卷弹簧的性能,设计了针对该多分支弹性单元的刚度标定实验。刚度标定平台如图 4所示,弹簧外轮与平台固定安装,弹簧内轮由伺服电机加载,其中伺服电机基于比例—微分(PI)控制器实现速度闭环控制。扭矩传感器用于测量电机对弹簧内轮施加的扭矩。扭簧材料选择高强度弹簧钢60Si2CrA,其弹性模量206 GPa、屈服极限1 568 Mpa,扭簧加工方式采用中走丝线切割,切割后喷丸处理。考虑弹性元件在外骨骼关节运动的实际工作场景,对刚度标定测试设计如下工作范式:

|
图 4 弹簧刚度测试平台 Fig.4 Test platform of spring stiffness |
(1) 以扭矩传感器为力矩反馈,将标定弹簧零力矩状态下的电机位置信息作为单次标定零点。
(2) 选取速度作为单次标定实验的加载速度。
(3) 电机执行匀速旋转运动,在形变测定区间
(4) 双向加载结束后电机牵引扭簧至零力矩位置,计算当前电机位置与标定零点间的位置偏差。若位置偏差超过1
(5) 调整加载速度,重复标定步骤(1)~(4)。
刚度标定实验中,在
|
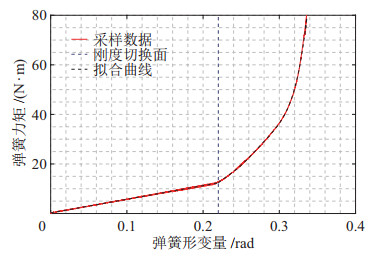
图 5 弹性元件在线性/非线性刚度区间内受力-形变关系 Fig.5 Force-deformation relationship of the elastic element in the linear/non-linear stiffness range |
|
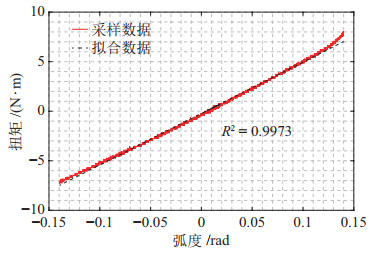
图 6 弹性元件在线性刚度区间内受力—形变关系 Fig.6 Force-deformation relationship of the elastic element in the linear stiffness range |
由图 5可知,弹性单元刚度存在显著分段现象,即刚度特性随弹性形变发生切换:当扭簧形变量小于0.224 rad时,扭簧受力—形变呈线性关系,刚度为57 N
定义刚度切换平面的额定形变区间为
| $ \tau_{{\text{spr}}} = \begin{cases} k\cdot \Delta d, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; | \Delta d |<0.22 \\ p_{1} \Delta d^{4}+p_{2} \Delta d^{3}+p_{3} \Delta d^{2}+p_{4} \Delta d+p_{5}, \;\; {\text{其他}} \end{cases} $ |
其中
事实上,变形量小于0.22 rad时各层扭簧间存在间隙,各层扭簧具有独立的线性刚度;当变形量大于0.22 rad后,相邻扭簧发生接触,且其接触面积随所受扭矩增大而增大,进而导致弹性元件的自由形变区间越来越小。得益于其结构特点,受外力影响,弹性单元在不同的形变区间将改变自身的受力状态,故其在较大形变下具有非线性刚度特性。相较于具有固定刚度的弹性元件,所提出的设计方案在提高承载性能的同时,具有线性/非线性刚度多态特性。
所设计的弹性单元根据所受载荷情况切换线性/非线性刚度,其具体特性体现为:(1) 弹性单元具有非线性刚度当且仅当系统处于过载状态。受非线性刚度影响,弹性单元对于持续的过载力矩能快速响应,形变量在较短时间内收敛至稳态值,实现过载情况下的限位保护。对于瞬时过载情形,弹性元件的刚度特性由线性过渡至非线性以实现力矩平衡,并在载荷卸除后快速收敛至额定形变区间,因此弹性单元在冲击载荷下具有较大阻尼响应。(2) 弹性单元在额定形变区间内具有线性刚度,该区间内非线性特性不显著,等效刚度为常值,弹性元件对外部载荷呈现被动柔顺。
2.4 下肢外骨骼串联弹性关节现有的外骨骼机器人通常将驱动元件集中布置在关节处,使得关节轴向尺寸较大,同时连杆空间难以有效利用。故本文提出了一种分体式串联弹性关节,以优化关节紧凑性、提高连杆空间利用率。
所设计的串联弹性关节如图 7、8所示,其额定功率430 W,额定力矩51.8 N

|
图 7 串联弹性关节 Fig.7 Series elastic joints |
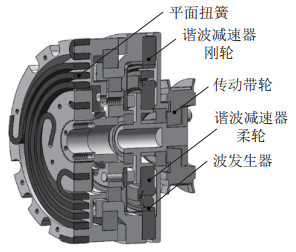
|
图 8 串联弹性关节传动结构 Fig.8 Transmission structure of series elastic joints |
串联弹性关节包含电机模块和减速器模块两部分,采用分体式设计。减速器输出轴与串联弹性关节旋转轴对齐,电机配置在连杆方向,模块间由同步齿形带传动。所设计的串联弹性关节搭载TQ-borodrive ILM50x08盘式电机与Harmonic CSD-20-100-GR-BB谐波减速器,其中新型弹性单元与谐波减速器中的波发生器配合构成串联弹性驱动器。串联弹性关节在外骨骼矢状面具有主动自由度,为防止人机交互过程中其他方向的力矩对关节造成损坏,在关节前后连杆间安装交叉滚子轴承从而保护弹性单元与谐波减速器。串联弹性关节通过双编码器分别测量电机角度(采用Posital公司的KCD-BC00B传感器测量)与弹簧形变量(采用RLS公司RM08SC传感器测量),电机及各传感器数据由关节内的电机驱动器(Synapticon公司,型号NODE E.1000)通过EtherCAT通信协议传输至主控制器。
串联弹性关节中,运动首先通过电机转子—转轴传递至电机端同步带轮,再由同步带传递至减速器端同步带轮,进而由减速器输出端传递至扭簧,最终驱动末端连杆。模块化关节等效传动效率
| $ \tau_{{\text{mot}}} = \begin{cases} \tau_{{\text{current}}} \cdot \eta, \;\;\; {\rm sgn }(\dot{\theta} \cdot \tau_{{\text{current}}})>0 \\ \tau_{{\text{current}}} /\eta, \;\;\; {\rm sgn }(\dot{\theta} \cdot \tau_{{\text{current}}})\leqslant 0 \end{cases} $ |
其中,
所设计的串联弹性关节兼具刚性连杆结构与柔性元件的动力学特性,构成刚柔耦合动力学模型。该关节的动力学模型基于以下基本假设:
假设 1:在刚度切换特性下,关节发生较大形变时受其结构特性影响会进行收敛运动,而关节形变较小时对关节柔性的影响近似为线性。
假设 2:驱动电机与负载连杆具有独立自由度。
假设 3:串联弹性关节的驱动元件被建模为质心位于关节旋转轴上的均匀刚体。
单关节串联弹性关节传动模型如图 9所示,其中连杆位置记为
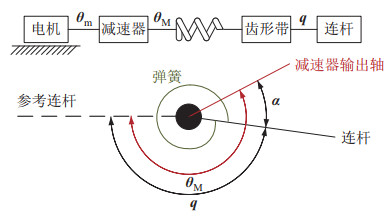
|
图 9 串联弹性关节传动图解模型 Fig.9 Schematic model of series elastic joints transmission |
为实现基于模型的控制算法设计,首先对串联弹性关节的动力学模型特性进行分析。对广义物理系统,由拉格朗日法建立系统动力学模型:
| $ F_{i} =\frac{\rm d}{{\rm d} t}\frac{\partial L}{\partial \dot{q}_{i}} -\frac{\partial L}{\partial q_{i}}, \quad i=1, 2, \cdots, n \\ L =T-P $ | (2) |
其中,
| $ P=P_{{\text{grav}}} +P_{{\text{elas}}} $ | (3) |
由假设2可知,重力引入的势能
| $ P_{{\text{grav}}} =P_{{\text{grav, link}}} ({\boldsymbol{q}})+P_{{\text{grav, motor}}} ({\boldsymbol{q}}) $ | (4) |
对于弹性势能
| $ P_{{\text{elas}}} =\frac{1}{2}({\boldsymbol{q}}-{\boldsymbol{\theta}}_{\rm M})^{\rm T} {\boldsymbol{K}}( {\boldsymbol{q}}-{\boldsymbol{\theta}}_{\rm M}) $ | (5) |
类似的,由假设2,系统总动能
| $ T =T_{{\text{link}}} +T_{{\text{motor}}} \\ T_{{\text{link}}} =\frac{1}{2}{\boldsymbol{\dot{q}}}^{\rm T}{\boldsymbol{M}}_{\rm L} ({\boldsymbol{q}}){\boldsymbol{\dot{q}}} \\ T_{{\text{motor}}} =\sum\limits _{i=1}^n \frac{1}{2}\left(m_{{\rm r}i} {\boldsymbol{v}}_{{\rm r}i}^{\rm T} {\boldsymbol{v}}_{{\rm r}i} +{\boldsymbol{\omega}}_{{\rm r}i}^{\rm T} {\boldsymbol{I}}_{{\rm r}i} {\boldsymbol{\omega}}_{{\rm r}i}\right) $ | (6) |
其中,
串联弹性关节动力学模型由刚性连杆子模型、电机—弹簧子模型构成。为建立完整的动力学模型,对串联弹性关节进行分步解耦建模。
(1) 刚性连杆子模型
利用投影牛顿-欧拉方法(projected Newton-Euler)建立刚性连杆的动力学模型并设置模型参数。连杆动力学基本模型为
| $ {\boldsymbol{M}}_{\rm L} ({\boldsymbol{q}}){\boldsymbol{\ddot{q}}}+{\boldsymbol{C}}({\boldsymbol{q}}, \dot{\boldsymbol q}){\boldsymbol{\dot{q}}}+ {\boldsymbol{G}} ({\boldsymbol{q}}) =\boldsymbol \tau $ | (7) |
其中,
模型中各矩阵参数由下式计算:
| $ {\boldsymbol{M}}_{\rm L} ({\boldsymbol{q}}) =\sum\limits _{i=1}^N \left( {\boldsymbol{J}}_{{\rm S}i}^{\rm T} m_{i} {\boldsymbol{J}}_{{\rm S}i} +{\boldsymbol{J}}_{{\rm R}i}^{\rm T} {\boldsymbol{I}}_{i} {\boldsymbol{J}}_{{\rm R}i}\right) \\ {\boldsymbol{C}}({\boldsymbol{q}}, \dot{\boldsymbol q}){\boldsymbol{\dot{q}}} =\sum\limits _{i=1}^N \left({{\boldsymbol{J}}_{{\rm S}i}^{\rm T} m_{i} {\boldsymbol{\dot{J}}}_{{\rm S}i} {\boldsymbol{\dot{q}}}+{\boldsymbol{J}}_{{\rm R}i}^{\rm T} ({\boldsymbol I_{i} {\boldsymbol{\dot{J}}}_{{\rm R}i} {\boldsymbol{\dot{q}}}+{\boldsymbol{\varOmega}}_{i} \times {\boldsymbol{I}}_{i} {\boldsymbol{\varOmega}}_{i}})}\right) \\ {\boldsymbol{G}}({\boldsymbol{q}}) =\sum\limits _{i=1}^N \left({-{\boldsymbol{J}}_{{\rm S}i}^{\rm T} m_{i} {{\boldsymbol{g}}}}\right) $ |
其中,
(2) 电机—弹簧子模型
由拉格朗日动力学模型式(2)、系统势能模型式(3)与动能模型式(6),进一步地,电机引入的动能项描述为
| $ T_{{\text{motor}}} =\frac{1}{2}{\boldsymbol{\dot{q}}}^{\rm T} \left({\boldsymbol{M}}_{\rm R} ({\boldsymbol{q}})+{{\boldsymbol{S}}}({\boldsymbol{q}}){{\boldsymbol{B}}}^{-1}{{\boldsymbol{S}}}^{\rm T}({\boldsymbol{q}})\right){\boldsymbol{\dot{q}}}+\notag \\ {\boldsymbol{\dot{q}}}^{\rm T} {\boldsymbol{S}} ({\boldsymbol{q}}){\boldsymbol{\dot{\theta}}}_{\rm M} +\frac{1}{2}{\boldsymbol{\dot{\theta}}}_{\rm M}^{\rm T} {\boldsymbol{B}}\dot{\boldsymbol \theta}_{\rm M} $ | (8) |
其中,
结合弹簧柔性引入的弹性势能式(5) 与拉格朗日方程(2),导出串联弹性关节动力学模型为
| $ \begin{pmatrix} {\boldsymbol{H}}({\boldsymbol{q}}) & {\boldsymbol{S}}({\boldsymbol{q}}) \\ {\boldsymbol{S}}^{\rm T}({\boldsymbol{q}}) & {\boldsymbol{B}} \end{pmatrix} \begin{pmatrix} {\boldsymbol{\ddot{q}}} \\ {\boldsymbol{\ddot{\theta}}}_{\rm M} \end{pmatrix}+ \begin{pmatrix} {\boldsymbol{C}}({\boldsymbol{q}}, \dot{\boldsymbol q})+{\boldsymbol{c}}_{1} ({\boldsymbol{q}}, \dot{\boldsymbol q}, \dot{\boldsymbol \theta}) \\ {\boldsymbol{c}}_{2} ({\boldsymbol{q}}, \dot{\boldsymbol q}) \end{pmatrix}+ \notag \\ \quad \begin{pmatrix} {\boldsymbol{G}}({\boldsymbol{q}})+{\boldsymbol{K}}({\boldsymbol{q}}-{\boldsymbol{\theta}}_{\rm M}) \\ {\boldsymbol{K}}({\boldsymbol{\theta}}_{\rm M} -{\boldsymbol{q}}) \end{pmatrix}= \begin{pmatrix} 0 \\ {\boldsymbol{\tau}}_{{\text{mot}}} \end{pmatrix} $ | (9) |
其中,
| $ {\boldsymbol{H}}({\boldsymbol{q}})={\boldsymbol{M}}_{\rm L} ({\boldsymbol{q}})+{\boldsymbol{M}}_{\rm R} ({\boldsymbol{q}})+{\boldsymbol{S}}({\boldsymbol{q}}){\boldsymbol{B}}^{-1}{\boldsymbol{S}}^{\rm T}({\boldsymbol{q}}) $ |
假设 4:对于较大的关节减速比,电机—连杆间惯量耦合引入的能量相对于系统总能量不显著,电机角速度仅由自身旋转决定。
在外骨骼康复应用场景中,串联弹性关节运动被约束在矢状面内,且连杆与电机连接处存在摩擦力。基于假设4对动力学模型式(9) 进行简化与修正:
(1) 科氏力项退化为平面形式:
| $ {\boldsymbol{C}}({\boldsymbol{q}}, {\boldsymbol{\dot{q}}}){\boldsymbol{\dot{q}}}=\sum\limits _{i=1}^n \left({\boldsymbol{J}}_{{\rm S}i}^{\rm T} m_{i} {\boldsymbol{\dot{J}}}_{{\rm S}i} {\boldsymbol{\dot{q}}}+{\boldsymbol{J}}_{{\rm R}i}^{\rm T} {\boldsymbol{I}}_{i} {\boldsymbol{\dot{J}}}_{{\rm R}i} {\boldsymbol{\dot{q}}}\right) $ |
此外,科氏力项
(2) 由假设4,电机—连杆耦合矩阵
(3) 当关节进行反向驱动时,摩擦力对外力的阻碍作用将被放大。考虑库仑力与黏滞摩擦力模型,引入库仑摩擦系数
| $ \tau_{\rm f}^{i} =\tau_{\rm k}^{i} {\rm{sgn}}({\dot{\theta}}_{{\rm M}, i})+D_{\rm v}^{i} {\dot{\theta}}_{{\rm M}, i} $ |
(4) 串联弹性关节中弹簧运动具有阻尼
基于上述讨论,面向控制系统设计的退化动力学模型为
| $ \begin{gathered} {\boldsymbol{H}}({\boldsymbol{q}}){\boldsymbol{\ddot{q}}}+{\boldsymbol{C}}({\boldsymbol{q}}, {\boldsymbol{\dot{q}}}){\boldsymbol{\dot{q}}}+{\boldsymbol{G}}({\boldsymbol{q}})+{\boldsymbol{\tau}}_{\rm f} -{\boldsymbol{K}}({\boldsymbol{\theta}}_{\rm M} -{\boldsymbol{q}}) ={\bf 0} \\ {\boldsymbol{B}}\ddot{{\boldsymbol\theta}}_{\rm M} +{\boldsymbol{K}}( {\boldsymbol{\theta}}_{\rm M} - {\boldsymbol{q}})+{\boldsymbol{D}}_{\rm s} ({\boldsymbol{\dot{\theta}}}_{\rm M} -{\boldsymbol{\dot{q}}}) ={\boldsymbol{\tau}}_{{\text{mot}}} \end{gathered} $ | (10) |
其中,
一般地,机器人系统辨识问题需要设计激励轨迹以充分激励系统并获得充分的辨识数据[22]。由退化动力学模型式(10) 可知,待辨识模型包含连杆变量
| $ {\boldsymbol{Y}}_{{\text{red}}} ({\boldsymbol{q}}, {\boldsymbol{\dot{q}}}, {\boldsymbol{\ddot{q}}}) {\boldsymbol{\varPhi}}_{{\text{red}}} ={\boldsymbol{H}}({\boldsymbol{q}}){\boldsymbol{\ddot{q}}}+{\boldsymbol{C}}({\boldsymbol{q}}, {\boldsymbol{\dot{q}}}){\boldsymbol{\dot{q}}}+{\boldsymbol{G}}({\boldsymbol{q}}) $ |
其中,
激励轨迹模型选择高阶傅里叶级数式(11),以获得微分连续且具有周期性的激励信号。
| $ q_{i} (t)=\sum\limits _{l=1}^{n_{\rm f}} a_{l}^{i} \sin (w_{\rm f} \textit{ltTs})-b_{l}^{i} \cos (w_{\rm f} \textit{ltTs}) +a_{i0} $ | (11) |
选取D-optimality准则[23]建立最优化问题,目标函数式(12) 为回归矩阵行列式的最大值。最优化问题中决策变量为傅里叶级数参数组
| $ \min\limits _{a_{\rm l}^{i}, b_{\rm l}^{i}, a_{i0}} -\log \left(\det ({\boldsymbol{Y}}_{{\text{red}}}^{\rm T} {\boldsymbol{Y}}_{{\text{red}}})\right) $ | (12) |
辨识激励实验中,通过参数整定后的PD控制器进行参考轨迹的位置追踪。为有效激励弹簧特性,对连杆输出端配置等效负重,激励轨迹频率选取200 Hz,并持续进行20次的轨迹激励。对数据低通滤波和时间平均处理后,激励实验结果如图 10所示。
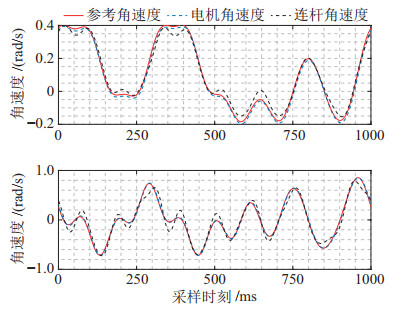
|
图 10 串联弹性关节辨识激励实验 Fig.10 Identification excitation of series elastic joints |
动力学模型式(10) 中,电机侧动力学与连杆侧动力学通过弹簧力矩
(1) 将弹簧力矩作为系统内力建立等效动力学模型:
| $ {\boldsymbol{H}}({\boldsymbol{q}}){\boldsymbol{\ddot{q}}}+{\boldsymbol{B}}\ddot{{\boldsymbol\theta}}_{\rm M} +{\boldsymbol{C}}({\boldsymbol{q}}, {\boldsymbol{\dot{q}}}){\boldsymbol{\dot{q}}}+{\boldsymbol{G}}({\boldsymbol{q}})+{\boldsymbol{\tau}}_{\rm f} ={\boldsymbol{\tau}}_{{\text{mot}}} $ | (13) |
进而对解耦模型式(13) 作线性分离:
| $ {\boldsymbol{Y}}_{{\text{dec}}}{\boldsymbol{\varPhi}}_{{\text{dec}}} = {\boldsymbol{H}}({\boldsymbol{q}}){\boldsymbol{\ddot{q}}}+{\boldsymbol{B}}\ddot{{\boldsymbol\theta}}_{\rm M}+ {\boldsymbol{C}}({\boldsymbol{q}}, {\boldsymbol{\dot{q}}}){\boldsymbol{\dot{q}}}+{\boldsymbol{G}}({\boldsymbol{q}})+{\boldsymbol{\tau}}_{\rm f} $ | (14) |
(2) 结合退化动力学模型式(10) 与线性分离模型式(14),对弹簧刚度与弹簧阻尼系数进行参数辨识。2.2节中,对串联弹性关节的弹性单元进行了离线刚度标定,而本节中对弹簧刚度进行系统辨识的另一目的是补偿关节装配误差。此时,待辨识动力学模型为
| $ {\boldsymbol{B}}\ddot{{\boldsymbol\theta}}_{\rm M} +{\boldsymbol{K}} ({\boldsymbol{\theta}}_{\rm M} -{\boldsymbol{q}})+{\boldsymbol{D}}_{\rm s} ({\boldsymbol{\dot{\theta}}}_{\rm M} -{\boldsymbol{\dot{q}}})={\boldsymbol{\tau}}_{{\text{mot}}} $ |
对应的线性分离参数化形式为
| $ {\boldsymbol{Y}}_{{\text{spr}}} {\boldsymbol{\varPhi}}_{{\text{spr}}} ={\boldsymbol{B}}\ddot{{\boldsymbol\theta}}_{\rm M} +{\boldsymbol{K}}({\boldsymbol{\theta}}_{\rm M} -{\boldsymbol{q}})+{\boldsymbol{D}}_{\rm s} ({\boldsymbol{\dot{\theta}}}_{\rm M} -{\boldsymbol{\dot{q}}}) $ |
对动力学模型式(10) 解耦后,采用带约束的最小二乘法进行参数辨识,将串联弹性关节在CAD设计软件中的参考计算值作为约束条件中的下界。为验证参数辨识结果的有效性,基于辨识结果进行逆动力学计算以获取电机力矩估计值,并与辨识过程中电机实际力矩进行对比,其中对电流环测量值进行零相位滤波以处理测量噪声。本文以单自由度串联弹性关节为对象进行了参数辨识实验,其逆动力学验证如图 11所示,参数辨识结果如表 1所示。
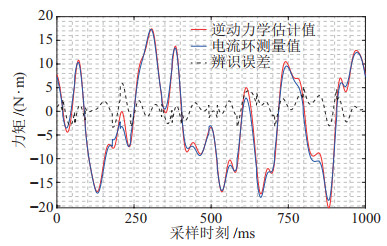
|
图 11 辨识参数逆动力学验证 Fig.11 Inverse dynamics verification of identification parameters |
|
|
表 1 动力学辨识参数 Tab. 1 Identified dynamic parameters |
串联弹性关节适用于在下肢康复外骨骼矢状面运动,受重力项与摩擦力作用,系统具有非线性。同时具有自主运动能力的外骨骼需要考虑系统控制功耗,并有效抑制交互过程中的外部环境扰动。控制器应满足如下设计需求:
(1) 控制器能够实现控制约束,避免控制量出现尖峰与抖动以提高交互舒适性;
(2) 控制器能够有效抑制交互过程中的输入输出扰动,具有鲁棒性。
基于退化动力学模型式(10),以单自由度串联弹性关节为被控对象设计控制算法,从而建立非线性最优化问题,并在模型预测控制(MPC)框架下进行数值求解。针对非线性模型预测控制(NMPC)的数值计算难点,利用线性化方法沿系统状态轨迹对原系统进行迭代变换和周期性更新,最终结合Laguerre网络对控制律进行滚动优化。
4.1 非线性优化问题设计将前述动力学模型式(10) 等效为单输入单输出(SISO)非线性系统:
| $ \begin{cases} {\boldsymbol{\dot{x}}}={\boldsymbol{f}}({\boldsymbol{x}})+{\boldsymbol{g}}({\boldsymbol{x}})u \\ y=x_{1} \end{cases} $ | (15) |
其中,
| $ {\boldsymbol{x}} =[x_{1} \; x_{2} \; x_{3} \; x_{4} ]^{\rm T} =[q \; \dot{q} \; \theta_{\rm M} \; \dot{\theta}_{\rm M} ]^{\rm T}\\ {\boldsymbol{f}}({\boldsymbol{x}}) = \begin{pmatrix} x_{2} \\ \dfrac{K(x_{3} -x_{1})-Cx_{2} -mgd\sin x_{1}-\tau_{\rm f} (x_{4})}{H} \\ x_{4} \\ -\dfrac{K(x_{3} -x_{1})+D_{\rm s} (x_{4} -x_{2})}{B} \end{pmatrix} \\ {\boldsymbol{g}}({\boldsymbol{x}}) = \left(0 \; 0 \; 0 \; \frac{1}{B} \right)^{\rm T}, \qquad u=\tau_{\rm M} $ |
系统在
| $ J(k)=\| {\boldsymbol{x}}^{ k}-{\boldsymbol{x}}_{\rm d}^{ k}\|^{2}+| u^{ k}-u_{\rm d}^{ k} |^{2} \\ {\text{s.t. }} \begin{cases} u_{\min}^{ k} \leqslant u^{ k} \leqslant u_{\max}^{ k} \notag\\ \dot{{\boldsymbol{x}}}^{ k}={\boldsymbol{f}}({\boldsymbol{x}}^{ k})+{\boldsymbol{g}}({\boldsymbol{x}}^{ k})u^{ k} \end{cases} $ | (16) |
其中,上标
系统状态方程(15) 存在重力项和摩擦力项而引入非线性因素,因而无法确保优化问题(16) 为凸优化问题,更进一步地,对优化问题(16) 的直接求解不能确保全局最优解的存在性。NMPC的求解首先需要对非凸问题进行凸化,并利用数值方法进行在线计算[24]。然而目前主流的NMPC求解速度与问题规模相关,尤其对预测时域
任意时刻,名义连续系统一致满足非线性关系式(15),同时期望轨迹
| $ {\boldsymbol{\dot{x}}}_{\rm d} ={\boldsymbol{f}}({\boldsymbol{x}}_{\rm d})+{\boldsymbol{g}}({\boldsymbol{x}}_{\rm d})u $ | (17) |
考虑系统工作点
| $ {\boldsymbol{\dot{x}}} \approx {\boldsymbol{f}}({\boldsymbol{x}}_{\rm d})+{\boldsymbol{g}}({\boldsymbol{x}}_{\rm d})u+\frac{\partial {\boldsymbol{f}}}{\partial {\boldsymbol{x}}} \bigg| _{{\boldsymbol{x}}={\boldsymbol{x}}_{\rm d}} ({\boldsymbol{x}}-{\boldsymbol{x}}_{\rm d}) \notag \\ ={\boldsymbol{f}}({\boldsymbol{x}}_{\rm d})+{\boldsymbol{g}}({\boldsymbol{x}}_{\rm d})u+{\boldsymbol{J}}_{{\boldsymbol{f}}} ({\boldsymbol{x}})({\boldsymbol{x}}-{\boldsymbol{x}}_{\rm d}) $ | (18) |
其中,
令矩阵
| $ {\boldsymbol{\dot{\tilde{x}}}}={\boldsymbol{J}}_{\boldsymbol f} ({\boldsymbol{x}})\tilde{{\boldsymbol{x}}}+{\boldsymbol{g}}({\boldsymbol{x}})\tilde{u} ={\boldsymbol{A}}_{\rm L} (t)\tilde{{\boldsymbol{x}}}+{\boldsymbol{B}}_{\rm L} (t)\tilde{u} $ | (19) |
进一步,对连续系统式(19) 进行欧拉离散化,得到离散线性时变(LTV)系统:
| $ \begin{split} \tilde{{\boldsymbol{x}}}(k+1)& ={\boldsymbol{A}}_{k} \tilde{{\boldsymbol{x}}}(k)+{\boldsymbol{B}}_{k} \tilde{{u}}(k) \\ \tilde{y}(k)& ={\boldsymbol{C}}_{k} \tilde{{\boldsymbol{x}}}(k) \end{split} $ | (20) |
考虑
| $ \min\limits _{\tilde{u}_{k} \in { U}} J(k) \\ {\text{s.t. }} \begin{cases} \tilde{{\boldsymbol{x}}}(k+1)={\boldsymbol{A}}_{k} \tilde{{\boldsymbol{x}}}(k)+{\boldsymbol{B}}_{k} \tilde{u}(k) \\ \tilde{{\boldsymbol{x}}}(k)={\boldsymbol{x}}(k)-{\boldsymbol{x}}_{\rm d} (k) \\ \tilde{u}(k)=u(k)-u_{\rm d} (k) \end{cases}\notag $ | (21) |
其中,
| $ \tilde{{\boldsymbol{x}}}^{\rm T}(k+N |k){\boldsymbol{P}} \tilde{{\boldsymbol{x}}}(k+N |k)+\sum\limits _{i=1}^{N-1} \tilde{{\boldsymbol{x}}}^{\rm T}(k+i| k){\boldsymbol{Q}} \tilde{{\boldsymbol{x}}}(k+i| k)+ \\ \quad \sum\limits _{i=1}^{N-1} R\tilde{u}^{2}( k+i |k)=J(k) $ |
为使系统在
| $ {\boldsymbol{P}}-{\boldsymbol{A}}^{\rm T}{\boldsymbol{PA}} = {\boldsymbol{Q}} $ | (22) |
一般地,在
基于Laguerre网络,
| $ \Delta u(k+m) ={\boldsymbol{L}}^{\rm T}(m){\boldsymbol{\eta}}_{k} \\ {\boldsymbol{L}}(m) =[l_{1} (m), l_{2} (m), \cdots, l_{N_{\rm L}} (m)]^{\rm T} \\ {\boldsymbol{\eta}}_{k} =[c_{1}, c_{1}, \cdots, c_{N_{\rm L}}]^{\rm T} $ | (23) |
其中
则当前时刻的最优控制输入可描述为
| $ \Delta \tilde{u}^{*} (k)={\boldsymbol{L}}^{\rm T}(0){\boldsymbol{\eta}}_{k} $ |
假设 5:存在
假设 6:预测时域
假设 7:在较高的系统控制频率下,系统状态量
定理 1:在假设5~7成立的条件下,对LTV系统式(20) 求1阶差分,系统可等效为带有积分器的增广模型:
| $ {\boldsymbol{X}}(k+1) ={\boldsymbol{AX}}(k)+{\boldsymbol{B}}\Delta u(k) \\ \tilde{y}(k) ={\boldsymbol{CX}}(k) $ | (24) |
其中,
| $ \begin{align*} {\boldsymbol{X}}(k) = \begin{pmatrix} \Delta {\boldsymbol{x}}(k) \\ \tilde{y}(k) \end{pmatrix}\\ {\boldsymbol{A}} =\begin{pmatrix} {\boldsymbol{A_{k}}} & {\bf 0} \\ {\boldsymbol{CA}}_{k} &{\boldsymbol{I}} \end{pmatrix}, \;\;{\boldsymbol{B}}=\begin{pmatrix} {\boldsymbol{B_{k}}} \\ {\boldsymbol{CB}}_{k} \end{pmatrix}, \;\;{\boldsymbol{C}}=\begin{pmatrix} {\bf 0} \\ {\boldsymbol{I}} \end{pmatrix}^{\rm T} \end{align*} $ |
若满足条件:
1) 最优化问题式(21) 在
2) 算法1对最优化问题具有可行解
那么,增广系统式(24) 关于原点是渐近稳定的。
算法1迭代线性化MPC算法
输入: 给定权重矩阵
1: 计算线性化轨迹
2: 根据初值条件
3: 结合Laguerre网络对凸优化问题式(21) 求解最优控制增量
4:
5:
6: 更新非线性系统式(15) 控制量
7:
证明:首先考察LTV系统式(20),易知
| $ | \cos x(k) -\cos x(k-1) |\leqslant \Delta x(k) <\varepsilon $ |
对系统1阶作差分计算,则
| $ \Delta \tilde{{\boldsymbol{x}}}(k+1) ={\boldsymbol{A}}_{k} \tilde{{\boldsymbol{x}}}(k) -{\boldsymbol{A}}_{k-1} \tilde{{\boldsymbol{x}}}(k-1) +{\boldsymbol{B}}_{k} \tilde{u}_{k} -{\boldsymbol{B}}_{k-1} \tilde{u}(k-1) \\ \approx {\boldsymbol{A}}_{k} (\tilde{{\boldsymbol{x}}}(k) -\tilde{{\boldsymbol{x}}}(k-1))+{\boldsymbol{B}}_{k} (\tilde{u}(k) -\tilde{u}(k-1)) \\ ={\boldsymbol{A}}_{k} \Delta \tilde{{\boldsymbol{x}}}(k) +{\boldsymbol{B}}_{k} \Delta \tilde{u}(k) $ |
根据假设4,当预测时域
| $ \prod\limits _k^N {\boldsymbol{A}}_{k} \approx {\boldsymbol{A}}_{k}^{N} $ |
在预测时域为
| $ {\boldsymbol{Y}}={\boldsymbol{F}}{\boldsymbol x}(k)+{\boldsymbol{\varPhi}} \Delta {\boldsymbol{U}} $ | (25) |
其中,
| $ \begin{align*} {\boldsymbol{\varPhi}} & = \begin{pmatrix} {\boldsymbol{C}}_{k} {\boldsymbol{B}}_{k} & 0 & \cdots & 0 \\ {\boldsymbol{C}}_{k} {\boldsymbol{A}}_{k} {\boldsymbol{B}}_{k} & {\boldsymbol{C}}_{k} {\boldsymbol{B}}_{k} & \cdots & 0 \\ \vdots & \vdots & \cdots & 0 \\ {\boldsymbol{C}}_{k} \displaystyle \prod _k^{N-1} {\boldsymbol{A}}_{k} {\boldsymbol{B}}_{k} & {\boldsymbol{C}}_{k} \displaystyle \prod _k^{N-2} {\boldsymbol{A}}_{k} {\boldsymbol{B}}_{k} & \cdots & {\boldsymbol{C}}_{k} \displaystyle \prod _k^{N-N_{\rm c}} {\boldsymbol{A}}_{k} {\boldsymbol{B}}_{k} \end{pmatrix}_{N\times N_{\rm c}} \\ & \approx \begin{pmatrix} {\boldsymbol{C}}_{k} {\boldsymbol{B}}_{k} & 0 & \cdots & 0 \\ {\boldsymbol{C}}_{k} {\boldsymbol{A}}_{k} {\boldsymbol{B}}_{k} & {\boldsymbol{C}}_{k} {\boldsymbol{B}}_{k} & \cdots & 0 \\ \vdots & \vdots & \cdots & 0 \\ {\boldsymbol{C}}_{k} {\boldsymbol{A}}_{k}^{N-1}{\boldsymbol{B}}_{k} & {\boldsymbol{C}}_{k} {\boldsymbol{A}}_{k}^{N-{2}}{\boldsymbol{B}}_{k} & \cdots & {\boldsymbol{C}}_{k} {\boldsymbol{A}}_{k}^{N-N_{\rm c}}{\boldsymbol{B}}_{k} \end{pmatrix}_{N\times N_{\rm c}} \\ {\boldsymbol{F}}& = \begin{pmatrix} {\boldsymbol{C}}_{k} {\boldsymbol{A}}_{k} \\ {\boldsymbol{C}}_{k} {\boldsymbol{A}}_{k}^{2} \\ \vdots \\ {\boldsymbol{C}}_{k} {\boldsymbol{A}}_{k}^{N} \end{pmatrix}_{N\times 1}, \quad \Delta {\boldsymbol{U}}= \begin{pmatrix} \Delta u(k) \\ \Delta u(k+1) \\ \vdots \\ \Delta u(k+N_{\rm c} -1) \end{pmatrix}_{N_{\rm c} \times 1} \\ {\boldsymbol{Y}}& =( y(k+1), y(k+2), \cdots, y(k+N) )^{\rm T} \end{align*} $ |
即LTV系统式(20) 等效为增广系统式(24)。
现证明增广系统式(24) 关于原点是渐近稳定的。在
| $ V(\tilde{{\boldsymbol{x}}}(k), k) =\bar{J}(k) \notag \\ =\tilde{{\boldsymbol{x}}}^{\rm T}(k+N |k){\boldsymbol{P}}\tilde{\boldsymbol x}(k+N |k)+ \notag \\ \quad \sum\limits _{i=1}^{N-1} \tilde{{\boldsymbol{x}}}^{\rm T}(k+i| k ){\boldsymbol{Q}}\tilde{\boldsymbol x}(k+i| k) +\notag \\ \quad \sum\limits _{i=0}^{N-1} {R}(\Delta \tilde{u}^{*} (k+i|k))^{2} $ | (26) |
易知李雅普诺夫函数
| $ \Delta \tilde{{\boldsymbol{U}}}_{k}^{*} =[\Delta \tilde{u}^{*} (k |k), \Delta \tilde{u}^{*} (k+1 |k), \cdots, \Delta \tilde{u}^{*} (k+N-1 |k)] \\ =[{\boldsymbol{L}}^{\rm T}(0)\boldsymbol \eta_{k}, {\boldsymbol{L}}^{\rm T}(1)\boldsymbol \eta_{k}, \cdots, {\boldsymbol{L}}^{\rm T}(N-1)\boldsymbol \eta_{k}] $ |
将
| $ \Delta {\boldsymbol{\bar{U}}}_{k+1}^{*} =[{\boldsymbol{L}}^{\rm T}(1)\boldsymbol \eta_{k}, {\boldsymbol{L}}^{\rm T}(2)\boldsymbol\eta_{k}, \cdots, {\boldsymbol{L}}^{\rm T}(N-1)\boldsymbol\eta_{k}, 0] $ |
为
| $ \begin{align*} V(\tilde{{\boldsymbol{x}}}(k+1), k+1)-V(\tilde{{\boldsymbol{x}}}(k), k) \\ \leqslant \bar{V}(\tilde{{\boldsymbol{x}}}(k+1), k+1)-V(\tilde{{\boldsymbol{x}}}(k), k) \end{align*} $ |
注意到
| $ \begin{align*} \bar{V}(\tilde{{\boldsymbol{x}}}(k+1), k+1)-V(\tilde{{\boldsymbol{x}}}(k), k) \\ =-\tilde{{\boldsymbol{x}}}^{\rm T}(k+1){\boldsymbol{Q}}\tilde{{\boldsymbol{x}}}(k+1)-\Delta \tilde{u}^{2}(k){R}<0 \end{align*} $ |
由李雅普诺夫定理可知,
| $ \tilde{{\boldsymbol{x}}}(k+1)\to 0, \quad k\to \infty $ |
即闭环系统关于原点
集成串联弹性关节的下肢外骨骼机器人如图 12所示。外骨骼机器人具备单侧三关节主动自由度,以实现人体矢状面内髋—膝—踝关节运动。主控制器对下肢运动轨迹进行解耦,将关节间的耦合运动划分为单关节子任务,最后由驱动器实现底层控制。本文以外骨骼机器人的髋关节模块为对象,基于所提出的算法设计了控制实验,并对实验结果进行分析。实验中,各控制参数如表 2所示。以PD前馈控制律[26]作为对比算法:
| $ \begin{split} u =K_{\rm P, m} (\theta_{\rm d} -\theta_{\rm M})-K_{\rm D, m} (\dot{\theta}_{\rm d} -\dot{\theta}_{\rm M})+\tau_{\rm ff} \\ \tau_{\rm ff} =B \ddot{\theta}_{\rm d} +K(\theta_{\rm d} -q_{\rm d}) \end{split} $ | (27) |

|
图 12 集成串联弹性关节的下肢外骨骼系统 Fig.12 Lower extremity exoskeleton system with series elastic joints |
|
|
表 2 实验参数定义与数值 Tab. 2 The definition and value of experimental parameters |
其中
为量化控制性能,定义如下评价指标:
(1) 平均绝对值误差为所有实际输出与期望输出的绝对值误差算术平均:
| $ e_{\text{MAE}} =\frac{1}{N}\sum\limits _{t=1}^N | y_{{\text{actual}}, {t}} -y_{{\text{desired}}, {t}} | $ | (28) |
(2) 均方根误差为实际输出与期望输出的偏差平方相比于统计次数的算术平方根:
| $ e_{\text{RMSE}} =\sqrt{\frac{1}{N}\sum\limits _{t=1}^N (y_{{\text{actual}}, {t}} -y_{{\text{desired}}, {t}})^{2}} $ | (29) |
(3) 控制能耗采用串联弹性关节中电机控制力矩的绝对平均值表征:
| $ J_{\text{EST}} =\frac{1}{N}\sum\limits _{k=1}^N | u(k) | $ | (30) |
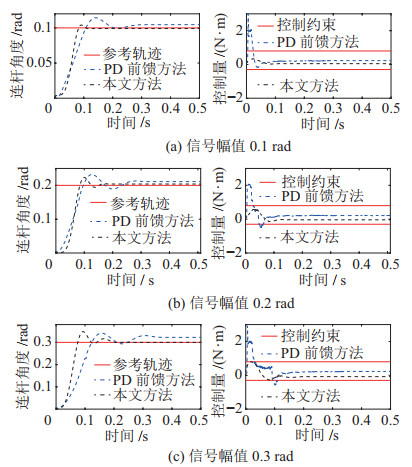
外骨骼运动控制中对关节姿态具有定位需求,例如关节初始姿态复位、姿态保持等场景任务。以阶跃参考轨迹为实例,设计3组不同幅值的参考轨迹以模拟关节姿态定位任务。其中,幅值分别选取为0.1 rad、0.2 rad、0.3 rad,实验结果如图 13及表 3所示。
|
图 13 串联弹性关节定位运动实验 Fig.13 Positioning experiment of the series elastic joint |
|
|
表 3 定位运动实验控制效果评估 Tab. 3 Control evaluation of the positioning experiment |
对于不同的信号幅值,本文方法都能够较快地(0.2 s内)收敛至目标值附近(稳态误差
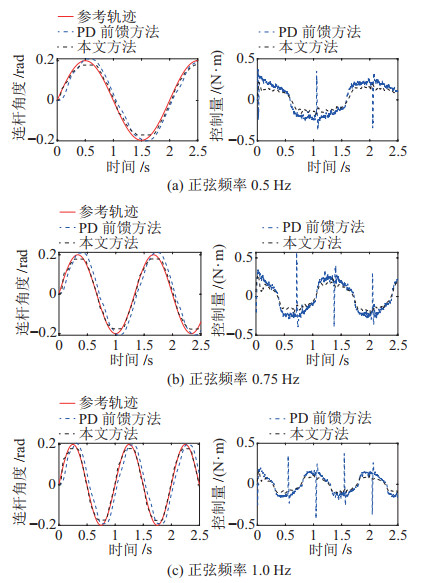
如前述,本文算法验证中以独立的髋关节为研究对象。下肢步态运动中,不同步速下髋关节位置轨迹均呈现类正弦曲线。为验证串联弹性关节运动跟踪性能,以不同周期的正弦轨迹为参考位置,分别取正弦频率为0.5 Hz、0.75 Hz、1 Hz以对应不同步态速度,信号幅值为0.2 rad。实验结果如图 14及表 4所示,本文方法与对比算法相比具有更低的相位延迟,这是因为基于模型的控制方法有效提升了系统的控制带宽,并显著优于对比方法中前馈项对模型动力学的补偿。
|
图 14 串联弹性髋关节运动跟踪实验 Fig.14 Tracking experiment of the series elastic hip joint |
|
|
表 4 跟踪实验的控制评估 Tab. 4 Control evaluation of the tracking experiment |
2种方法在控制过程中均满足控制约束(电机输出力矩处于
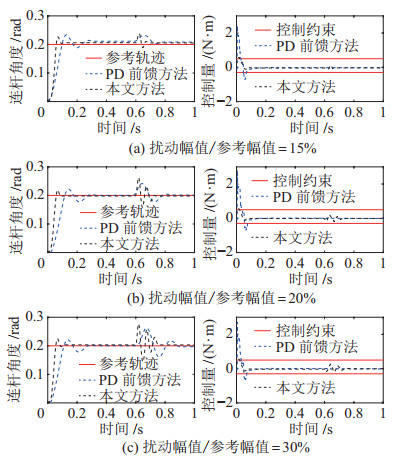
外骨骼设备在人机交互中存在外部环境及穿戴者的扰动,对系统提出了鲁棒性要求。在5.1节的基础上,设计了系统稳态下发生外部冲击扰动的实验。所设计的扰动发生时刻位于稳定的位置跟踪阶段,以模拟串联弹性关节进行位置定位和姿态保持时突然受到外部扰动的情景。扰动实验中,阶跃参考信号的幅值为0.2 rad,扰动发生时刻为0.6 s,设计扰动大小分别为参考信号幅值的15%、20%、30%,实验结果如图 15及表 5所示。
|
图 15 脉冲扰动下系统输出与控制量 Fig.15 System output and control under pulse disturbance |
|
|
表 5 扰动抑制实验的控制评估 Tab. 5 Control evaluation of the disturbance rejection experiment |
对比算法中缺乏对外部扰动的主动调节,但串联弹性关节具有被动柔顺性,在扰动结束后连杆位置仍能回到参考轨迹,因此在本实验中,对比算法退化为被动扰动抑制情形。本文方法在扰动发生后的0.1 s内回到参考轨迹,同时扰动发生前后控制量一致满足控制约束。在未进行主动扰动响应的对比算法中,连杆位置在扰动发生后的0.3 s内回到参考轨迹邻域,伴随小幅度的稳态误差,收敛时间随扰动增加而显著延长。实验结果表明本文方法对外部扰动具有抑制作用,验证了算法的鲁棒性。
对比算法中缺乏对外部扰动的主动调节,但串联弹性关节具有被动柔顺性,在扰动结束后连杆位置仍能回到参考轨迹,因此在本实验中,对比算法退化为被动扰动抑制情形。本文方法在扰动发生后的0.1 s内回到参考轨迹,同时扰动发生前后控制量一致满足控制约束。在未进行主动扰动响应的对比算法中,连杆位置在扰动发生后的0.3 s回到参考轨迹邻域,伴随小幅度的稳态误差,收敛时间随扰动增加而显著延长。实验结果表明本文方法对外部扰动具有抑制作用,验证了算法的鲁棒性。
5.4 系统带宽实验所设计的串联弹性关节对系统引入弹性环节,进而对系统控制带宽产生影响。为计算系统在所提出算法下的实际控制带宽,设计了带宽实验。在迭代线性化模型预测控制中,控制内环为电机力矩控制,最外环为连杆位置控制。外骨骼设备在康复应用场景中的主要任务是对患者下肢的运动功能进行复现,即利用外骨骼引导患者下肢运动并实现对期望轨迹的跟踪,因此本文围绕系统位置带宽进行实验设计。
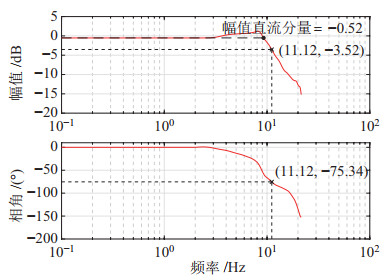
实验中以5 kg均匀质量块等效患者下肢大腿质量[27],并与串联弹性关节的连杆侧固定。设计正弦线性变频连杆位置信号
| $ r(t)=A\sin \left(\phi_{0} +2\pi \left(f_{0} t+\frac{k}{2}t^{2}\right)\right) $ |
其中,
实验对串联弹性关节进行时间长度为200 s的位置跟踪控制,并分别对期望信号和实际输出信号进行快速傅里叶变换以得到频域下的增益与相位。其中,采用零相位滤波器对所需数据进行了低通滤波以降低测量噪声。所得系统闭环Bode图如图 16所示。其中,幅值直流分量为
|
图 16 闭环系统Bode图 Fig.16 Bode diagram of the closed loop system |
由于具有较高柔顺性,所提出的串联弹性关节难以获得刚性系统的高带宽,与SEA相关文献[28-29]相比,本文方法实现了较好的带宽控制,能够覆盖人体下肢运动的频率范围[30]。在康复外骨骼的临床应用中,下肢运动功能障碍患者相比于健康人群具有更低的运动频率。目前商用康复外骨骼频率为0.5~0.8 Hz[31],本文提出的控制方法能够满足康复外骨骼频率需求。
6 结论(Conclusion)针对下肢康复外骨骼系统,提出了一种紧凑、轻量化的串联弹性关节,并设计了一种迭代线性化模型预测控制方法。该关节具有独有的刚度切换特性,在利用非线性刚度对抗过载形变以提供结构保护的同时,能够保证额定工作区间内具有一致的线性刚度。为实现控制器设计,本文首先对串联弹性关节进行了系统能量分析与动力学建模,并实现分步解耦动力学参数辨识以及对应的激励和验证实验;其次建立了最优化问题框架,设计了迭代线性化模型预测控制以求解带有控制量约束的非线性非凸优化问题。针对外骨骼任务场景,对姿态定位任务、髋关节步态跟踪任务设计了对比实验。实验结果表明,本文方法能够实现串联弹性关节的运动跟踪并对控制量进行有效约束,从而避免控制量出现尖峰与抖动,降低了系统控制能耗并抑制了外部扰动。此外,基于模型的控制方法有效提升了柔性关节的控制带宽以适应复杂人机交互场景。本文提出的串联弹性关节能够作为柔顺交互的关节模组,被拓展应用于不同自由度的外骨骼与相关柔顺交互控制任务中。
| [1] |
Virani S, Alonso A, Benjamin E J, et al. Heart disease and stroke statistics-2022 update: A report from the American Heart Association[J]. Circulation, 2022, E153-E639. |
| [2] |
The GBD 2016 Lifetime Risk of Stroke Collaborators Lifetime Risk of Stroke Collaborators. Global, regional, and countryspecific lifetime risks of stroke, 1990 and 2016[J]. New England Journal of Medicine, 2018, 379(25): 2429-2437. DOI:10.1056/NEJMoa1804492 |
| [3] |
程洪, 黄瑞, 邱静, 等. 康复机器人及其临床应用综述[J]. 机器人, 2021, 43(5): 606-619. Cheng H, Huang R, Qiu J, et al. A survey of rehabilitation robot and its clinical applications[J]. Robot, 2021, 43(5): 606-619. DOI:10.13973/j.cnki.robot.200570 |
| [4] |
Yan T, Cempini M, Oddo C M, et al. Review of assistive strategies in powered lower-limb orthoses and exoskeletons[J]. Robotics and Autonomous Systems, 2015, 64: 120-136. DOI:10.1016/j.robot.2014.09.032 |
| [5] |
侯增广, 赵新刚, 程龙, 等. 康复机器人与智能辅助系统的研究进展[J]. 自动化学报, 2016, 42(12): 1765-1779. Hou Z G, Zhao X G, Cheng L, et al. Recent advances in rehabilitation robots and intelligent assistance systems[J]. Acta Automatica Sinica, 2016, 42(12): 1765-1779. DOI:10.16383/j.aas.2016.y000006 |
| [6] |
赵新刚, 谈晓伟, 张弼. 柔性下肢外骨骼机器人研究进展及关键技术分析[J]. 机器人, 2020, 42(3): 365-384. Zhao X G, Tan X W, Zhang B. Development of soft lower extremity exoskeleton and its key technologies: A survey[J]. Robot, 2020, 42(3): 365-384. |
| [7] |
Kwa H K, Noorden J H, Missel M, et al. Development of the IHMC mobility assist exoskeleton[C]//IEEE International Conference on Robotics and Automation. Piscataway, USA: IEEE, 2009: 2556-2562.
|
| [8] |
Sankai Y. HAL: Hybrid assistive limb based on cybernics[M]//Robotics Research. Berlin, Germany: Springer, 2010: 25-34.
|
| [9] |
Esquenazi A, Talaty M, Packel A, et al. The ReWalk powered exoskeleton to restore ambulatory function to individuals with thoracic-level motor-complete spinal cord injury[J]. American Journal of Physical Medicine & Rehabilitation, 2012, 91(11): 911-921. |
| [10] |
Tan X W, Zhang B, Liu G, et al. Cadence-insensitive soft exoskeleton design with adaptive gait state detection and iterative force control[J]. IEEE Transactions on Automation Science and Engineering, 2021, 19(3): 2108-2121. |
| [11] |
Pratt G, Williamson M. Series elastic actuators[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Human Robot Interaction and Cooperative Robots. Piscataway, USA: IEEE, 1995: 399-406.
|
| [12] |
Tagliamonte N, Accoto D. Passivity constraints for the impedance control of series elastic actuators[J]. Proceedings of the Institution of Mechanical Engineers, Part Ⅰ: Journal of Systems and Control Engineering, 2014, 228(3): 138-153. |
| [13] |
Kong K, Bae J, Tomizuka M. A compact rotary series elastic actuator for human assistive systems[J]. IEEE/ASME Transactions on Mechatronics, 2011, 17(2): 288-297. |
| [14] |
Calanca A, Fiorini P. Human-adaptive control of series elastic actuators[J]. Robotica, 2014, 32(8): 1301. DOI:10.1017/S0263574714001519 |
| [15] |
朱秋国, 熊蓉, 吕铖杰, 等. 新型串联弹性驱动器设计与速度控制[J]. 电机与控制学报, 2015, 19(6): 83-88. Zhu Q G, Xiong R, Lü C J, et al. Novel series elastic actuator design and velocity control[J]. Electric Machines and Control, 2015, 19(6): 83-88. |
| [16] |
王萌, 孙雷, 尹伟, 等. 一种面向交互应用的串联弹性驱动器有限时间输出反馈控制方法[J]. 机器人, 2016, 38(5): 513-521. Wang M, Sun L, Yin W, et al. A finite time output feedback control approach for interaction-oriented series elastic actuators[J]. Robot, 2016, 38(5): 513-521. |
| [17] |
陈朝峰, 杜志江, 张慧, 等. 基于柔性驱动关节的下肢外骨骼双模态切换控制[J]. 机器人, 2021, 43(5): 513-525. Chen C F, Du Z J, Zhang H, et al. Double-mode switching control of a lower limb exoskeleton based on flexible drive joint[J]. Robot, 2021, 43(5): 513-525. |
| [18] |
宋召鹏. 柔顺串联弹性驱动器的设计与控制方法研究[D]. 济南: 山东大学, 2020. Song Z P. Design and control method of compliant series elastic actuator[D]. Jinan: Shandong University, 2020. |
| [19] |
Gerlach-Hahn K, Dahmen C, Misgeld B J E. Design and evaluation of a serial elastic actuator for human assistance[C]//XXIV International Conference on Information, Communication and Automation Technologies (ICAT). Piscataway, USA: IEEE, 2013. DOI: 10.1109/ICAT.2013.6684087.
|
| [20] |
Kim S, Bae J. Force-mode control of rotary series elastic actuators in a lower extremity exoskeleton using model-inverse time delay control[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(3): 1392-1400. |
| [21] |
张庆超. 基于串联弹性驱动器的下肢外骨骼机器人研制[D]. 秦皇岛: 燕山大学, 2021. Zhang Q C. Development of lower limb exoskeleton based on series elastic actuator[D]. Qinhuangdao: Yanshan University, 2021. |
| [22] |
Bruno S, Oussama K. Springer handbook of robotics[M]. Berlin, Germany: Springer, 2016: 287-295.
|
| [23] |
Stephen B, Lieven V. "Statistical estimation" in convex optimization[M]. Cambridge, UK: Cambridge University Press, 2009: 351-396.
|
| [24] |
Frank A, Alex Z. Nonlinear model predictive control[M]. Basel, Switzerland: Birkhäuser, 2012.
|
| [25] |
Wang L. Model predictive control system design and implementation using MATLAB®[M]. Berlin, Germany: Springer Science & Business Media, 2009.
|
| [26] |
Khalil H K. Nonlinear control[M]. New York, USA: Pearson Higher, 2014.
|
| [27] |
de Leva P. Adjustments to Zatsiorsky-Seluyanov's segment inertia parameters[J]. Journal of Biomechanics, 1996, 29(9): 1223-1230. |
| [28] |
Kim D, Koh K, Cho G R, et al. A robust impedance controller design for series elastic actuators using the singular perturbation theory[J]. IEEE/ASME Transactions on Mechatronics, 2019, 25(1): 164-174. |
| [29] |
Oh S, Kong K. High-precision robust force control of a series elastic actuator[J]. IEEE/ASME Transactions on Mechatronics, 2016, 22(1): 71-80. |
| [30] |
Kong K, Bae J, Tomizuka M. Control of rotary series elastic actuator for ideal force-mode actuation in human-robot interaction applications[J]. IEEE/ASME Transactions on Mechatronics, 2009, 14(1): 105-118. |
| [31] |
Li Y Q, Fan T, Qi Q, et al. Efficacy of a novel exoskeletal robot for locomotor rehabilitation in stroke patients: A multi-center, non-inferiority, randomized controlled trial[J]. Frontiers in Aging Neuroscience, 2021, 13. DOI:10.3389/fnagi.2021.706569 |
 2023, Vol. 45
2023, Vol. 45


