2. 上海理工大学中德国际学院, 上海 200093;
3. 上海理工大学光电信息与计算机工程学院, 上海 200093;
4. 之江实验室, 浙江 杭州 311100
2. Sino-German College, University of Shanghai for Science and Technology, Shanghai 200093, China;
3. School of Optical-Electrical and Computer Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China;
4. Zhejiang Lab, Hangzhou 311100, China
机器人技术正处在类似于早期互联网发展阶段中的晶体管时代[1]。其中,水下仿生机器人因其广泛的应用领域(国防安全、资源勘查、深水探险、水环境生态保护、医疗保健等),近年来一直是研究热点。随着智能软材料科学的不断进步,依靠其特性延展出了不同的驱动方式,这为软体仿生机器人的研究及实际应用带来了许多新的方向。
对于机器人系统,动力与控制是其重要的组成模块,对机器人的应用方式与场景有着决定性的作用[2]。软体仿生机器人的自身结构因其各自驱动方式的不同而有所差异,现阶段的主要驱动方式有介电弹性体(DE)[3]、流体驱动(气动[4]、液动[5])、形状记忆合金(SMA)[6]、磁驱动[7]、离子交换聚合物金属复合材料(IPMC)[8]、响应水凝胶驱动[9]等。软体机器人驱动方式主要体现以下几个特点:(1) 软体机器人的运动方式依赖于其驱动器自身产生的变形。通过对驱动器进行可编程控制,可以实现样机的运动控制,来满足实际应用需求。(2) 由于驱动方式不同,样机自身的驱动力和响应精度也有很大的差别。(3) 驱动方式的多样性拓展了仿生机器人应用场景的多样性,这促进了多学科(生物、医疗、化学、材料、机械、基础物理力学等)的交叉融合。
双稳态结构不需要持续输入能量,可以进行2个稳定状态的跳变切换(snap-through)[10],机构装置简单,驱动装置具有优越的驱动性能,目前已有许多国内外的学者对其进行多领域的研究。浙江大学李铁风团队[11]提出了一种基于双稳态结构的DE膜驱动方法,该驱动器只需要一个高压脉冲来驱动结构进行前后运动,具有机电跳变不稳定性。美国坦普尔大学Tang等[12]模仿猎豹奔跑时快速拉伸脊背的运动状态,制作了一种依靠双稳态装置跳变产生驱动力的奔跑软体机器人(地面运动速度可达187.5 mm/s,约2.68倍身长/秒(以下写作BL/s))和水下软体机器人(水中游动速度可达117 mm/s,约0.78 BL/s)。西安交通大学Li等[13]受骨骼—肌腱结构运动机理的启发,设计了一种具有快速机械响应和较高机械力协同作用的电活性双稳态驱动器(EBA),EBA利用其自身放大机制的不稳定性来调节输出力和响应时间,并将其应用到仿生机器人爬行(直线运动速度0.56 mm/s)和跳跃(跳跃高度95 mm)中。
基于乌贼喷水推进机理的水下机器人同样具有较强的应用前景,喷水推进是水下生物如乌贼、鱿鱼和水母等的主要运动形式,与摆尾摆鳍的游动方式相比,其具有较高的推进效率[14]。北京航空航天大学Hou等[15]制作了一种喷水推进鱿鱼样机,该样机模仿自然界中飞乌贼下水、喷射、滑翔和潜水的游动原理,利用自身可折叠和展开的软体变形鳍和臂,可以实现从水中到空中的快速穿梭。青岛大学Tang等[16]合作研发的仿头足类水下机器人使用DE作为驱动器,采用喷水推进运动方式,游动速度可以达到33 mm/s (0.43 BL/s)。美国加州大学Christianson等[17]研制了一种可以通过改变腔体体积和横截面积,实现可重复喷射推进的仿头足类水下机器人,该样机通过内部齿轮齿条的运动,带动柔软身体进行扩张和收缩,产生推力向前游动,其平均游动速度可达184 mm/s(0.54 BL/s)。
目前,采用双稳态驱动的仿生机器人仍依赖弹簧、连杆等刚性机构进行预拉伸积聚势能[11-12],结构复杂,制作成本也较高。本文制作了一种结构简单、力学性能良好的双稳态装置,克服了软材料响应速度慢的缺点,具有较高驱动功率,并将其作为驱动装置应用到仿乌贼结构水下软体机器人的喷水推进中。
2 双稳态驱动装置工作原理(Working principle of the bistable driving device) 2.1 驱动装置设计传统弓箭主要由弓臂和弓弦组成,弓弦固定在弓臂两端,射箭时通过拉伸弓弦使弓身弯曲变形积聚势能,释放弓弦的瞬间弓身的势能也会释放,推动弓箭射向前方,如图 1(a)所示。依据弓箭工作原理,若将具有一定抗弯曲刚度的弹性基板通过外部结构挤压使其发生弯曲变形,到达位置1,如图 1(b)所示,则其也会由于自身弯曲而积聚势能。当外界对预弯曲的弹性基板施加外力扰动(图 1(c)),外力达到基板承受的临界值时,基板会发生跳变,到达位置2(图 1(d))。
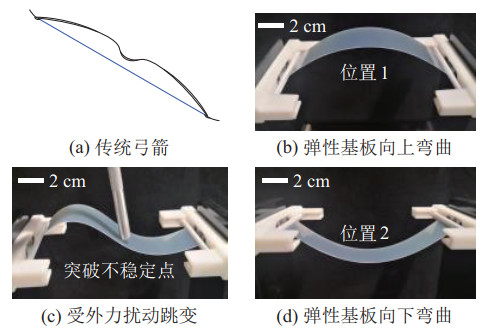
|
图 1 弹性基板弯曲示意图 Fig.1 Schematic diagram of elastic substrate bending |
从能量角度,跳变过程有2个稳定状态和1个不稳定状态。当基板处于上、下弯曲状态时,基板受外部结构限位不会发生位移运动,可以保持自身的弯曲,势能处于极小值点,进入稳定状态。而当施加外部扰动力时,由于两端对基板自由度的限制,使其只能发生波浪式变形来缓解受力,此时基板处于不稳定状态,内部势能处于一个极大值点。
本节搭建的驱动装置通过将气腔(人工肌肉)粘接在基板(骨骼)两侧来实现双稳态的弯曲和跳变,驱动装置结构尺寸如图 2所示,其中,气腔选用的材料是热塑性聚氨酯(TPU)薄膜,尺寸结构如图 2(a)所示。TPU薄膜材料作为一种新型环保材料,具有类似于橡胶的弹塑性,在高温条件下能够熔融粘合,具有一定的自修复特性[18],可以满足热压密封的需求。气腔的热封工具使用手压式塑封机,制作气腔时不需要预先设计模具,相对于复杂的热封(激光熔融热封等),本文气腔制作简便且成本更低,气腔制作过程如图 3(a)所示。
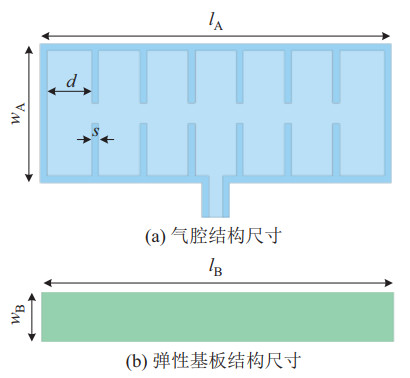
|
图 2 驱动装置结构尺寸 Fig.2 Structural dimensions of the driving device |
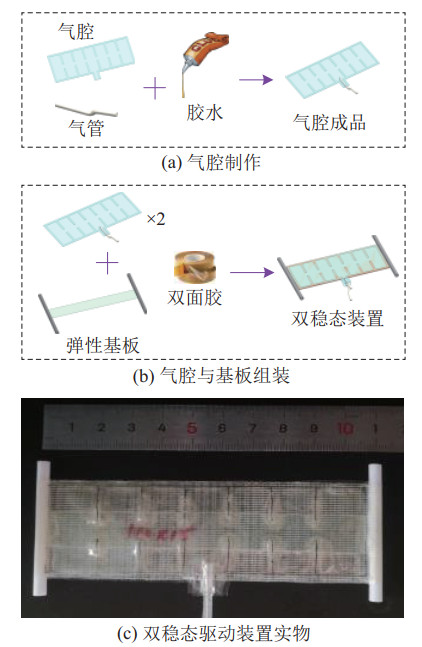
|
图 3 双稳态驱动装置制作过程 Fig.3 Manufacturing process of the bistable driving device |
基板是气腔的骨骼支撑元件,由双面胶将气腔粘附在弹性模量较高的基板上,使其在变形时能够拉动基板发生弯曲。设计中选用FR-4环氧树脂基板作为基板材料,其外形尺寸如图 2(b)所示,样机中使用的基板尺寸
根据实际需要,装置的尺寸可以进行相应的调整。双稳态驱动装置实物如图 3(c)所示,其材料参数如表 1所示,对于不同尺寸的驱动装置,其工作稳定性关键在于气腔的气密性以及基板能否克服临界力产生跳变。
|
|
表 1 双稳态驱动装置材料参数 Tab. 1 Material parameters of the bistable driving device |
双稳态驱动装置通过壳体自身结构使FR-4弹性基板产生预弯曲,如图 4(a)所示,进而积聚并转移弹性势能来实现稳态的跳变,分析时可将其视作屈曲梁。

|
图 4 双稳态装置预弯曲受力简图 Fig.4 Pre-bending force diagram of the bistable device |
驱动装置两端通过壳体夹具限位在
驱动装置自身系统的能量主要来自于弹性基板弯曲的应变能与轴向载荷挤压产生的内能。
| $ \begin{align} W_{\rm T} =W_{\rm S} +W_{\rm H} +W_{\rm E} \end{align} $ | (1) |
式中,
| $ \begin{align} y(x)= \sum\limits_{n=1}^{\infty} b_{n} \sin \frac{n\pi x}{l} \end{align} $ | (2) |
对双稳态驱动装置进行微元法分析,假设在某一点弯曲产生的切向位移是
| $ \begin{align} {\rm d}s-{\rm d}x={\rm d}x\sqrt{1+ \left(\frac{{\rm d}y}{{\rm d}x}\right)^{2}}-{\rm d}x\approx \frac{1}{2} \left(\frac{{\rm d}y}{{\rm d}x}\right)^{2}{\rm d}x \end{align} $ | (3) |
通过式(3) 可得双稳态驱动装置的原长
| $ \begin{align} \lambda =\frac{1}{2}\int_0^l \left(\frac{{\rm d}y}{{\rm d}x}\right)^{2} {\rm d}x \end{align} $ | (4) |
将式(2) 代入式(3),得到总差值
| $ \begin{align} \lambda =\frac{\pi^{2}}{4l} \sum\limits_{n=1}^{\infty} n^{2}b_{n}^{2} \end{align} $ | (5) |
根据图 4(b)中
| $ \begin{align} \theta \approx \frac{{\rm d}y}{{\rm d}x} \end{align} $ | (6) |
根据材料力学弯曲理论,双稳态驱动装置的弯矩
| $ \begin{align} \frac{{\rm d}^{2}y}{{\rm d}x^{2}}=\frac{M(x)}{EI} \end{align} $ | (7) |
其中,
| $ \begin{align} W_{\rm S} =\frac{1}{2}\int_0^l EI \left( \frac{{\rm d}^{2}y}{{\rm d}x^{2}} \right)^{2} {\rm d}x \end{align} $ | (8) |
通过式(2)(6) 可以计算出偏转角
| $ \begin{align} \theta =\frac{\pi} {l} \sum\limits_{n=1}^{\infty} nb_{n} \cos \frac{n \pi x}{l} \end{align} $ | (9) |
本文只考虑
| $ \begin{align} \theta_{0} & =\frac{{\rm d}y_{0}} {{\rm d}x_{0}} =\frac{\pi} {l} b_{1} \cos 0=\frac{ \pi b_{1}} {l} \end{align} $ | (10) |
| $ \begin{align} b_{1} & =\frac{l}{\pi} \theta_{0} \end{align} $ | (11) |
对式(2) 求2阶导数,计算系统内部应变能:
| $ \begin{align} \frac{{\rm d}^{2}y}{{\rm d}x^{2}}=-\frac{\pi^{2}}{l^{2}} \sum\limits_{n=1}^{\infty} n^{2}b_{n} \sin \frac{n \pi x}{l} \end{align} $ | (12) |
当
| $ \begin{align} W_{\rm S} =\frac{1}{2}\int_0^l EI \left(\frac{ \pi \theta_{0}} {l}\right)^{2}\sin^{2} \frac{ \pi x}{l}{\rm d}x \end{align} $ | (13) |
弹性基板的惯性矩
| $ \begin{align} I=\frac{w_{\rm B} h^{3}}{12} \end{align} $ | (14) |
其中,
| $ \begin{align} W_{\rm S} =\frac{Ew_{\rm B} \pi^{2}h^{3}}{48l}\theta_{0}^{2} \end{align} $ | (15) |
双稳态驱动装置受到轴向(
| $ \begin{align} \Delta l=\frac{F_{\rm H} l}{ES} \end{align} $ | (16) |
其中,
| $ \begin{align} L_{1}& =L_{0} -{\Delta} l=\int_0^l \sqrt{1+(y')^{2}} {\rm d}x\approx \int_0^l \left(1+\frac{1}{2}(y')^{2}\right) {\rm d}x \\ &=l+\lambda \end{align} $ | (17) |
由式(17) 可以得出
| $ \begin{align} F_{\rm H} =\frac{ES| L_{0} -\lambda -l |}{l} \end{align} $ | (18) |
取
| $ \begin{align} \lambda =\frac{1}{2}\int_0^l \frac{{\rm d}^{2}y}{{\rm d}x^{2}} {\rm d}x =\frac{\pi^{2}b_{1}^{2}} {4l}=\frac{l\theta_{0}^{2}} {4} \end{align} $ | (19) |
则
| $ \begin{align} W_{\rm H} =F_{\rm H} \lambda \end{align} $ | (20) |
将式(18) (19) 代入式(20) 可以得到轴向载荷产生内能的表达式为
| $ \begin{align} W_{\rm H} =ES \left(\frac{l}{16}\theta_{0}^{4} -\frac{L_{0} -l}{4}\theta_{0}^{2}\right) \end{align} $ | (21) |
气腔对基板做的功
| $ \begin{align} W_{\rm E} =2F_{1} \Delta y+7F_{2} \Delta d \end{align} $ | (22) |
式中
将式(15)(21)(22) 代入式(1),可得到系统内部总能量
| $ \begin{align} W_{\rm T} =\frac{ESl}{16}\theta_{0}^{4} -\frac{12ES({L_{0} -l})l-Ew_{\rm B} {\pi}^{2}h^{3}}{48l}\theta_{0}^{2} +W_{\rm E} \end{align} $ | (23) |
利用Matlab软件绘制式(23) 所示系统的能量曲线,结果如图 5所示。通过分析可知,当初始转角

|
图 5 双稳态装置能量曲线 Fig.5 Energy curve of the bistable device |
双稳态驱动装置临界跳变力
| $ \begin{align} F_{\rm B} =\frac{130.5EI\pi} {l^{3}} \sqrt{{\frac{\Delta y^{2}}{4l}-\frac{4.18I}{lS}}} \end{align} $ | (24) |
双稳态装置长度
| $ \begin{align} F_{\rm B} =\frac{10.875Eh^{3}\pi} {l^{3}} \sqrt{{\frac{3\Delta y^{2}-4.18h^{2}}{12l}}}w_{\rm B} \end{align} $ | (25) |
根据薄膜理论,分析气腔与基板粘合侧的受力状态,薄膜气腔受内压作用产生的薄膜应力为[20]
| $ \begin{align} \sigma =\frac{P_{\text{work}} r}{\Delta t} \end{align} $ | (26) |
式中,
| $ \begin{align} F_{\rm A} =\int_0^{l_{\rm B}} \sigma w_{\rm B} {\rm d}l \end{align} $ | (27) |
在双稳态驱动装置工作过程中,当气腔充气膨胀所产生的切换力大于基板的临界跳变力时,基板发生二次分叉屈曲跳变时会突破势能极大值点进行跳变。通过式(23) 和式(25) 可以推导出能量
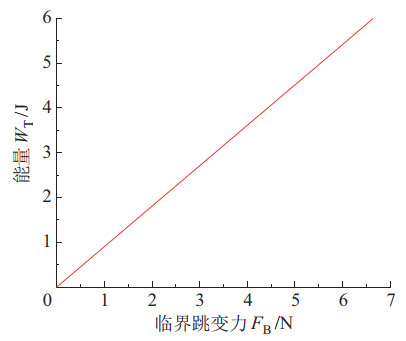
|
图 6 能量—临界跳变力曲线 Fig.6 Energy - critical jump force curve |
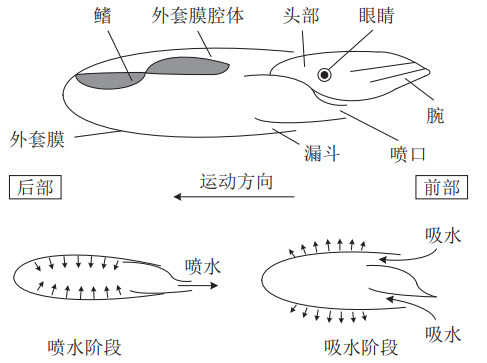
乌贼运动时主要通过喷水推进,其运动过程如图 7所示[21],每个运动周期包括吸水、喷水2个过程。在吸水时喷口关闭,外套膜扩张,使内部腔体产生负压,水经漏斗吸入体内。在喷水时,外套膜和漏斗连接处闭合,外套膜收缩,利用产生的收缩力对内部腔体的水进行挤压,将水从喷口快速排出产生推力,使乌贼高速运动。
|
图 7 乌贼喷水推进示意图 Fig.7 Schematic diagram of squid water-jet propulsion |
基于乌贼吸、排水运动机理,设计了一种通过腔体体积变化产生推进力的软体机器人,样机运动原理如图 8(a)所示。样机结构主要由上壳体、下壳体、双稳态驱动装置和拨水薄膜组成。拨水薄膜与双稳态驱动装置相连,驱动装置往复跳变,产生式(1) 中的能量变化,带动拨水薄膜往复运动产生体积变化

|
图 8 样机工作示意图 Fig.8 Working diagram of the prototype |
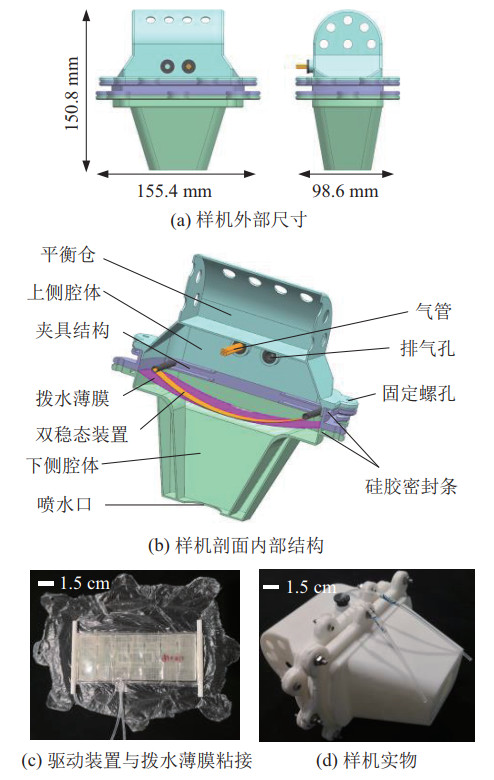
仿乌贼机器人样机外形尺寸如图 9(a)所示,外部壳体采用工业级光固化3D打印机(型号:联泰Lite600HD)加工,材料使用未来R4600类ABS树脂(密度1.13 ~1.16 g/cm
|
图 9 样机结构和实物 Fig.9 Prototype structure and physical objects |
双稳态驱动装置通过壳体夹具结构进行安装,夹具滑槽对驱动装置进行限位使其发生预弯曲。驱动装置与拨水薄膜通过强力布基双面胶相连,如图 9(c)所示,装配时拨水薄膜放置在双稳态装置下侧与水接触面上,双稳态装置安装在上侧腔体内部,避免与水接触。样机实物如图 9(d)所示,样机壳体质量144.7 g,样机零部件装配后总质量216.1 g。
由于双稳态驱动装置在跳变过程中,一侧接触介质为液体,另一侧为空气。如果对上侧腔体进行完全密封,则当双稳态驱动装置向内运动时,如图 10所示,上侧腔体内部产生正压(内部压力

|
图 10 上侧腔体密封状态对双稳态跳变的影响 Fig.10 Influence of the upper chamber seal state on the bistable snap-through |
在试验中发现,由于样机上侧腔体为密封状态,壳体密度接近于水,在水中会产生较大的浮力。为了克服自身浮力带来的影响,设计中利用样机的自身结构来调整浮力,在样机上侧腔体增加储水平衡仓,保证样机在水中的自平衡和浮沉性能。样机结构参数如表 2所示。
|
|
表 2 样机结构参数 Tab. 2 Prototype structure parameters |
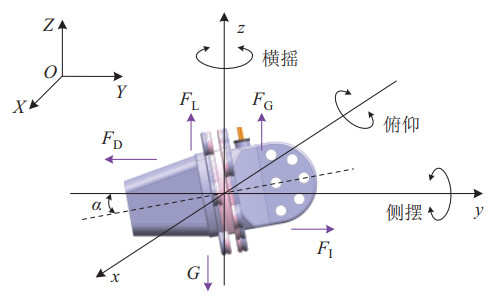
物体在水中游动时所受到的推力和阻力来源主要是惯性力和黏性力。雷诺数(
| $ \begin{align} { Re}=\frac{UL}{\nu} \end{align} $ | (28) |
式中,
通过计算,样机在最低驱动频率0.17 Hz下的游动速度为32.46 mm/s,雷诺数
| $ \begin{align} F=F_{\rm I}+F_{\rm D}+F_{\rm L}+F_{\rm G}+G \end{align} $ | (29) |
|
图 11 样机水中运动受力图 Fig.11 Force diagram of the prototype when moving in water |
式中,
由于样机在水中处于漂浮状态,故其重力和浮力数值相等,即推进力表达式为
| $ \begin{equation} \begin{split} &F_{\rm G}+G=0 \\ &F=F_{\rm I}+F_{\rm D}+F_{\rm L} \end{split} \end{equation} $ | (30) |
样机游动时处于高雷诺数状态,其所受黏滞阻力较小,自身形体产生阻力起主要作用,样机所受阻力
| $ \begin{align} F_{\rm D} =\frac{1}{2}C_{\rm D} \rho U^{2}S_{\rm D} \end{align} $ | (31) |
式中,
样机在游动时部分身体沉入水下,其运动时上表面的压力小于下表面而产生升力,升力
| $ \begin{align} F_{\rm L} =\frac{1}{2}C_{\rm L} \rho U^{2}S_{\rm L} \end{align} $ | (32) |
式中,
仿乌贼机器人推进方式为喷水推进,其惯性力
| $ \begin{equation} V(t) =V_{1} +V_{2}, \quad V_{1} =w_{\rm A} \int_{-\Delta y}^{\Delta y} y(x, t){\rm d}x \end{equation} $ | (33) |
式中,
样机在实际运动过程中,由于拨水薄膜自身存在褶皱,因而内部实际的充水量与理论充水量存在差别,且略小于理论充水量[21],
| $ \begin{align} V_{\rm C} (t)=V_{\rm R} +V(t)-V_{\max} \end{align} $ | (34) |
式中,
| $ \begin{align} F_{\rm I} (t) =\;& U_{\rm j} \frac{{\rm d}m}{{\rm d}t} =\frac{\partial } {\partial t}\int_{V_{\rm C}} U_{\rm j} (x, t)\rho {\rm d}V + \\ & \int_{S_{\rm C}} U_{\rm j} (x, t)\rho U_{\rm j} (x, t){\rm d}S_{\rm N} \end{align} $ | (35) |
式中,
| $ \begin{align} F_{\rm I} =\rho \frac{V_{\rm O}} {t}U_{\rm j} =\rho S_{\rm N} U_{\rm j}^{2} \end{align} $ | (36) |
式中,
双稳态装置的循环跳变促使下侧腔体内部液体产生周期性体积变化,下侧腔体是以开放式的形式与外部液体环境交互,通过控制双稳态装置的驱动频率实现缓慢吸水、快速排水,样机自身产生反向推力,实现样机前进运动。初次跳变时,样机产生初始速度,依靠惯性力,在样机停止运动前,双稳态驱动装置再次跳变,保证样机速度累积,样机游动中不出现后退现象,使其持续稳定地在水中运动。
4 试验与仿真(Experiment and simulation) 4.1 气腔测试气腔由2层TPU薄膜材料通过热封机进行高温熔融热封,制作方式简单易行。由热封机熔融热封出多个腔体隔断,气腔的隔断数不同,表现出不同的收缩性能,图 12(a)(b)分别展示了气腔未充气状态和充气收缩状态。

|
图 12 气腔充气收缩测试 Fig.12 Experiment of cavity filling shrinkage |
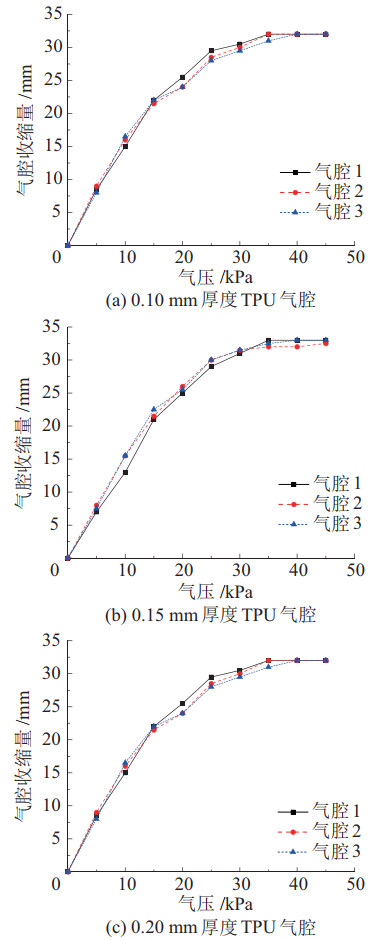
气腔的理论收缩量可利用式(37) 计算,当单个气腔隔断完全充气膨胀时,可以将其理想化为圆柱状,圆柱半径为
| $ \begin{equation} \begin{aligned} 2d & =2{\pi} r_{\rm cavity} \\ \Delta d & =d-2r_{\rm cavity} = \left(1-\dfrac{2}{\pi}\right)d \end{aligned} \end{equation} $ | (37) |
|
图 13 TPU气腔收缩量—气压试验测试 Fig.13 Testing of TPU cavity shrinkage-air pressure |
试验中气腔尺寸
TPU薄膜材料的厚度对气腔的拉伸力特性有一定的影响,为了选取合适厚度的TPU薄膜材料,对前文所述3种厚度材料制作的气腔进行对比实验,装置如图 14(a)所示。通过夹具固定气腔两端对其进行充气,改变气腔内部的气压,使用推拉力计测试不同气压下气腔产生的拉力值。
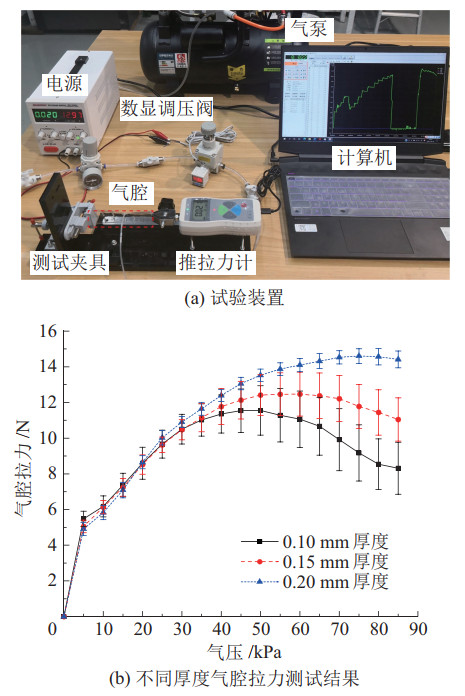
|
图 14 气腔拉力试验装置及结果 Fig.14 Experiment device and results of cavity tensile |
分析图 14(b)的试验结果,当内部气压大于60 kPa时,气腔材质越薄,其对拉力的保持性越弱,这是由于气腔发生弹性形变所致。气腔材质越厚,其对拉力的保持性越好,试验中厚度为0.15 mm和0.20 mm的TPU薄膜在工作压力45 ~65 kPa范围内具有较好的拉力保持性。热封TPU薄膜时发现,由热封0.20 mm厚度材料制作出的气腔整体气密性较差,在工作压力下易发生漏气现象,不能保证双稳态装置的稳定跳变,而由0.15 mm厚度材料制作的气腔气密性非常好,在满足试验要求的情况下,本文选择0.15 mm厚度的TPU薄膜材料制作双稳态驱动装置的气腔。
4.2 弹性基板测试与仿真为选取合适厚度的弹性基板,进行图 15所示的测试试验,分别选取厚度为0.10 mm、0.20 mm、0.30 mm的FR-4环氧树脂基板,基板长度设为
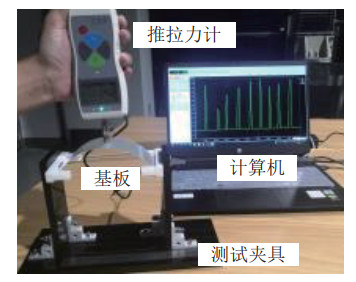
|
图 15 基板临界跳变力试验装置 Fig.15 Experiment device of the substrate critical jump force |
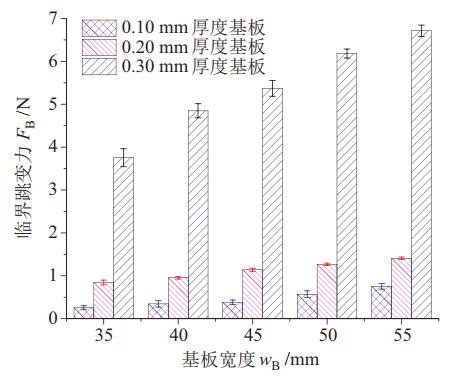
|
图 16 基板临界跳变力测试 Fig.16 Experiment of the substrate critical jump force |
分析图 16测试结果可知,相同宽度
对制作好的双稳态驱动装置进行跳变测试,偶尔会出现图 17中的跳变卡死现象,这是因为弹性基板受到两端均匀的气腔拉力,无法突破势能极大值点完成跳变。

|
图 17 双稳态驱动装置跳变卡死 Fig.17 Jumping stuck of the bistable driving device |
为了保证双稳态驱动装置的稳定跳变,设计中对基板进行图 18(a)所示的挖方孔处理,方孔宽为
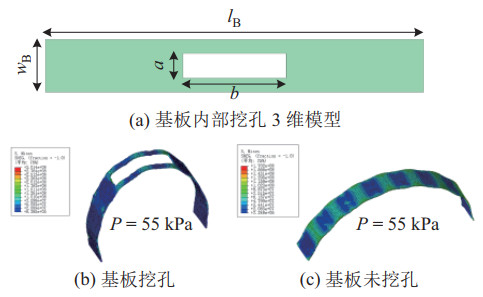
|
图 18 弹性基板挖孔处理 Fig.18 Hole-digging treatment of the elastic substrate |
为了对比内部挖孔和未挖孔处理的2种基板受气腔拉伸力影响的程度,使用ABAQUS软件对2种基板制作的驱动装置均施加气压
通过试验测试进一步对比2种基板的临界跳变力,结果如图 19所示。结果表明,未挖孔处理的基板临界跳变力约为挖孔处理基板的1.4倍,结合图 6分析,发现挖孔处理更易受到外界扰动,产生弯曲跳变。
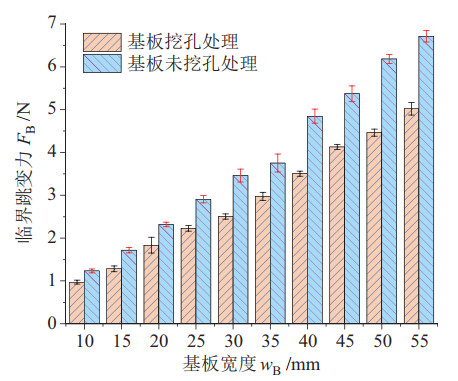
|
图 19 基板挖孔—未挖孔状态下的临界跳变力测试 Fig.19 Test of critical jump force for the dug and un-dug substrates |
气腔提供的切换力与弹性基板的稳态切换力具有一定的关系,基于式(24) 推导出的弹性基板临界跳变力与基板宽度之间的关系,对比实验数据拟合曲线与理论曲线,得到如图 20所示的结果。
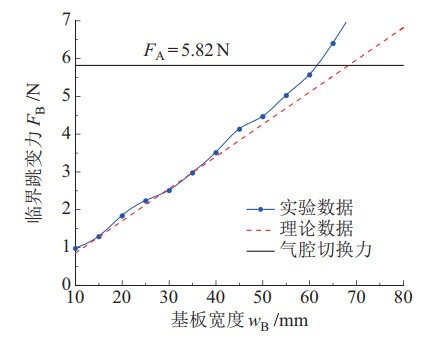
|
图 20 基板跳变力理论数据—试验数据对比曲线 Fig.20 Comparison curves of theoretical-experiment data of the substrate jumping force |
通过式(27) 计算出气腔作用于基板的切换力
|
|
表 3 双稳态驱动装置尺寸选取范围 Tab. 3 Size selection range of the bistable driving device |
对双稳态驱动装置的弯曲性能进行如图 21所示的测试,通过对驱动装置

|
图 21 双稳态装置弯曲性能测试 Fig.21 Bending performance test of the bistable device |
双稳态驱动装置弯曲角简图如图 4(c)所示,得出弯曲跨度
| $ \begin{align} l=\frac{2L_{0}} {\beta} \sin \frac{\beta} {2} \end{align} $ | (38) |
通过测量不同气压下的弯曲跨度
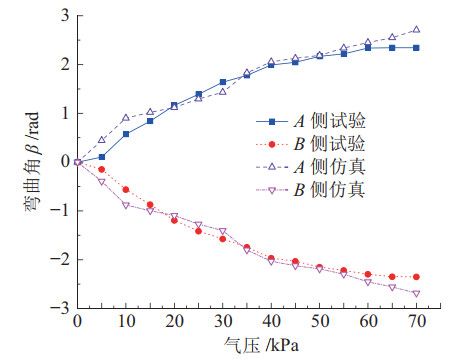
|
图 22 双稳态装置弯曲角—气压变化曲线 Fig.22 Bending angle-pressure variation curve of the bistable device |
为验证驱动装置是否可以稳定跳变,采用图 23所示的试验装置进行跳变测试,记录一个周期的跳变过程,如图 24所示。图 24(a)中,驱动装置在

|
图 23 双稳态驱动装置跳变测试装置 Fig.23 The snap-through test device of the bistable driving device |

|
图 24 双稳态驱动装置跳变过程 Fig.24 Snap-through process of the bistable driving device |
图 24(b)为
如图 24(e)所示,
试验结果表明,驱动装置在跳变中可以产生较大的驱动力,跳变时驱动力的释放会在很短的时间内完成,该驱动力可以作为本文中仿乌贼机器人喷水推进的驱动源。双稳态驱动装置的周期性跳变运动可以为仿乌贼机器人的喷水、充水循环运动提供可能性。文中试验硬件配置如表 4所示。
|
|
表 4 试验配置 Tab. 4 Experiment configuration |
利用图 23所示试验装置对样机进行水下游动测试,通过改变双稳态驱动装置的驱动频率来验证样机速度变化规律,结果如图 25所示。测试的驱动频率最小为0.17 Hz,此时样机平均游动速度为32.46 mm/s;驱动频率最大为0.67 Hz,此时样机平均游动速度为86.55 mm/s。对样机实测运动速度进行拟合,得出样机游动速度变化曲线,结果显示样机速度随着驱动装置驱动频率的增大而呈上升状态。
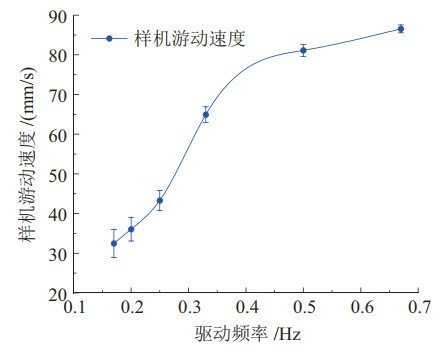
|
图 25 样机速度和频率关系图 Fig.25 The relationship diagram between the prototype speed and frequency |
仿乌贼结构样机在游动时可以根据自身结构进行浮力的调节,这为样机提供了一定的负重能力。试验表明,样机在水中的负重能力为227.7 g,当质量超过该数值时,样机游动效果较差,该负重能力为后期样机集成化设计提供了可能。
样机2个运动周期(4 s)的游动过程如图 26所示,驱动频率为0.5 Hz,样机的平均运动速度可以达到81.14 mm/s,表现出了优异的游动性能。然而,样机还存在以下不足:首先,样机只能进行带缆绳游动,拖动的气管在一定程度上会干扰样机的游动;其次,由于自身质量较轻,在喷水推进的过程中,受惯性力的作用,会出现前后俯仰的运动状态,后期需要对样机的重心进行优化,提高游动的稳定性;最后,样机还不能实现完全的潜游状态,在后续工作中,需要对上侧腔体结构进行改进,避免腔体内部压力对双稳态驱动装置跳变产生影响。

|
图 26 样机水中游动试验 Fig.26 Swimming experiment of the prototype in water |
试验初期发现,上侧腔体如果出现漏水现象,双稳态推进装置仍可以正常跳变,随着上侧腔体内部水体积的增加,样机的游动速度会受到影响,速度逐渐减小。试验中为了保证样机的游动性能,需要保证样机上侧腔体的密封性,避免水进入上侧腔体。
本文在样机设计中只应用了一个双稳态驱动装置,在后期的应用拓展中,可以将多个双稳态驱动装置进行模块化组合,为水下仿生样机的设计打开新的思路。根据时间的先后顺序,对近年水下仿生机器人进行了综合性能对比,结果如表 5所示。仿生机器人的驱动方式对其游动速度有很大的影响,随着智能材料的发展,水下仿生机器人的运动方式趋向于多样化,如喷水推进、胸鳍摆动、尾鳍摆动和脚蹼游动等。本文利用气动双稳态驱动装置优异的驱动性能,保证了样机在水中较好的游动性能,未来将根据不同应用场景进行新的改进和拓展。
|
|
表 5 水下仿生机器人性能对比 Tab. 5 Comparison of the underwater bionic robot performance |
本次样机设计使用气动双稳态驱动装置,软基板两侧连接的气腔可以保证结构的对称性,气腔膨胀需要的气量较少,换气成本低,响应迅速,驱动装置控制简单。现有的气动软体机器人多采用硅胶注模气动网格等形式[1],充放气形成弯曲形变,这类制作会增加生产成本,硅胶固化过程难以统一。本文的驱动装置在其跳变过程中可以产生稳定的驱动力,也为水下仿生机器人的研究提供了一种稳定、低成本的驱动方式,在水下环境中具有实际应用意义。
6 结论(Conclusion)本文通过将双稳态驱动装置与乌贼喷水前进的运动方式相结合,设计出一种气动双稳态驱动的仿乌贼结构喷水推进软体机器人。通过实际测试,驱动器可以满足样机的喷水前进运动方式,通过理论、仿真与试验分析得出以下结论:
(1) 建立了双稳态驱动装置的理论模型,进一步得出双稳态装置系统能量与临界跳变力呈正相关关系。
(2) 试验测试了双稳态驱动装置的跳变过程,分析了材料选型对于驱动装置性能的影响。使用ABAQUS软件对驱动装置弯曲角随气压变化的关系进行仿真,仿真与试验结果基本一致,验证了驱动装置的弯曲性能,得出双稳态驱动装置的稳定跳变可以向外输出稳定的驱动力。
(3) 对样机进行游动试验测试,试验表明双稳态装置具有优异的驱动性能,样机平均运动速度可以达到8.7 cm/s(0.58 BL/s),表现出良好的游动性能,且样机自身有一定的负重能力。
(4) 采用的气动双稳态驱动装置为水下仿生机器人的设计提供了新的驱动方式。后续工作将会对其进行模块化设计,应用到新的仿生驱动中,同时对样机进行改进,提升样机游动稳定性,将供气模块和供电模块集成到样机内部,实现脱缆绳自主游动。
| [1] |
Whitesides G M. Soft robotics[J]. Angewandte Chemie International Edition, 2018, 57(16): 4258-4273. DOI:10.1002/anie.201800907 |
| [2] |
Li T F, Li G R, Liang Y M, et al. Fast-moving soft electronic fish[J]. Science Advances, 2017, 3(4). DOI:10.1126/sciadv.1602045 |
| [3] |
Li G R, Chen X P, Zhou F H, et al. Self-powered soft robot in the Mariana Trench[J]. Nature, 2021, 591: 66-71. DOI:10.1038/s41586-020-03153-z |
| [4] |
南卓江, 杨扬, 铃森康一, 等. 基于细径McKibben型气动人工肌肉的仿生手研发[J]. 机器人, 2018, 40(3): 321-328. Nan Z J, Yang Y, Suzumori K, et al. Development of a bionic hand actuated by thin McKibben pneumatic artificial muscle[J]. Robot, 2018, 40(3): 321-328. |
| [5] |
Suzumori K, Faudzi A A. Trends in hydraulic actuators and components in legged and tough robots: A review[J]. Advanced Robotics, 2018, 32(9): 458-476. DOI:10.1080/01691864.2018.1455606 |
| [6] |
谢巧莲, 孟巧玲, 曾庆鑫, 等. 基于SMA驱动模块的腕部柔性外骨骼设计[J]. 机器人, 2021, 43(4): 406-413. Xie Q L, Meng Q L, Zeng Q X, et al. Design of a soft wrist exoskeleton based on SMA actuator module[J]. Robot, 2021, 43(4): 406-413. |
| [7] |
孙强, 王敬依, 张颖, 等. 毫米级潜艇形机器人在低雷诺数液体中的3D运动及微操作方法研究[J]. 机器人, 2020, 42(1): 89-99. Sun Q, Wang J Y, Zhang Y, et al. On 3D motion and micromanipulation of a millimeter-scale submarine-shaped robot in low Reynolds number liquid[J]. Robot, 2020, 42(1): 89-99. |
| [8] |
卞长生, 白万发, 朱子才, 等. 基于IPMC仿生机器鱼驱动技术研究[J]. 水下无人系统学报, 2019, 27(2): 149-156. Bian C S, Bai W F, Zhu Z C, et al. Research on actuating technology of IPMC-based biomimetic robotic fish[J]. Journal of Unmanned Undersea Systems, 2019, 27(2): 149-156. |
| [9] |
Yuk H, Lin S T, Ma C, et al. Hydraulic hydrogel actuators and robots optically and sonically camouflaged in water[J]. Nature Communications, 2017, 8. DOI:10.1038/ncomms14230 |
| [10] |
勾燕洁, 张守银, 陈贵敏. 一种全柔顺六稳态机构的设计[J]. 机械工程学报, 2015, 51(7): 61-66. Gou Y J, Zhang S Y, Chen G M. Design approach for a fully compliant sexastable mechanism[J]. Journal of Mechanical Engineering, 2015, 51(7): 61-66. |
| [11] |
Li T F, Zou Z A, Mao G Y, et al. Electromechanical bistable behavior of a novel dielectric elastomer actuator[J]. Journal of Applied Mechanics, 2014, 81(4). DOI:10.1115/1.4025530 |
| [12] |
Tang Y C, Chi Y D, Sun J F, et al. Leveraging elastic instabilities for amplified performance: Spine-inspired high-speed and high-force soft robots[J]. Science Advances, 2020, 6(19). DOI:10.1126/sciadv.aaz6912 |
| [13] |
Li D C, Niu D, Ye G Y, et al. Crawling-jumping synergic bioinspired robots harnessing electroactive bistable actuators by adjusting mechanical responses and forces[J]. Applied Materials Today, 2021, 24. DOI:10.1016/J.APMT.2021.101091 |
| [14] |
王振龙, 李健, 杭观荣, 等. 生物喷水推进机理及其在仿生喷水推进装置中的应用[J]. 机器人, 2009, 31(3): 281-288. Wang Z L, Li J, Hang G R, et al. Mechanism of jet propulsion in aquatic life and its application to biomimetic jet propulsion vehicles[J]. Robot, 2009, 31(3): 281-288. |
| [15] |
Hou T G, Yang X B, Su H H. et al. Design and experiments of a squid-like aquatic-aerial vehicle with soft morphing fins and arms[C]//International Conference on Robotics and Automation. Piscataway, USA: IEEE, 2019: 4681-4687.
|
| [16] |
Tang C, Ma W T, Li B, et al. Cephalopod-inspired swimming robot using dielectric elastomer synthetic jet actuator[J]. Advanced Engineering Materials, 2020, 22(4). DOI:10.1002/adem.201901130 |
| [17] |
Christianson C, Cui Y, Ishida M, et al. Cephalopod-inspired robot capable of cyclic jet propulsion through shape change[J]. Bioinspiration & Biomimetics, 2020, 16(1). DOI:10.1088/1748-3190/abbc72 |
| [18] |
Kim J T, Kim B K, Kim E Y, et al. Synthesis and properties of near IR induced self-healable polyurethane/graphene nanocomposites[J]. European Polymer Journal, 2013, 49(12): 3889-3896. |
| [19] |
赵剑, 贾建援, 王洪喜, 等. 双稳态屈曲梁的非线性跳跃特性研究[J]. 西安电子科技大学学报(自然科学版), 2007, 34(3): 458-462. Zhao J, Jia J Y, Wang H X, et al. Nonlinear snap-through characteristic of a compressed bi-stable buckled beam[J]. Journal of Xidian University (Natural Science), 2007, 34(3): 458-462. |
| [20] |
苗常青, 祖振南, 王首骞, 等. 充气囊体力学性能试验研究[J]. 载人航天, 2018, 24(3): 383-387. Miao C Q, Zu Z N, Wang S Q, et al. Experimental study on mechanical properties of inflatable cabin[J]. Manned Spaceflight, 2018, 24(3): 383-387. |
| [21] |
Anderson E J, DeMont M E. The mechanics of locomotion in the squid loligo pealei: Locomotory function and unsteady hydrodynamics of the jet and intramantle pressure[J]. Journal of Experimental Biology, 2000, 203(18): 2851-2863. |
| [22] |
Jordan C E. A model of rapid-start swimming at intermediate Reynolds number: Undulatory locomotion in the chaetognath sagitta elegans[J]. Journal of Experimental Biology, 1992, 163(1): 119-137. |
| [23] |
Yang Y, Liu J K, Cai C W. Analytical solutions to stress concentration problem in plates containing rectangular hole under biaxial tensions[J]. Acta Mechanica Solida Sinica, 2008, 21: 411-419. |
| [24] |
牛传猛, 毕树生, 蔡月日, 等. 胸鳍摆动推进仿生鱼的设计及水动力实验[J]. 机器人, 2014, 36(5): 535-543. Niu C M, Bi S S, Cai Y R, et al. Design and hydrodynamic experiments on bionic robotic fish with oscillating pectoral fins[J]. Robot, 2014, 36(5): 535-543. |
| [25] |
Li X B, Yu J Z. Design and simulation of a robotic jellyfish based on mechanical structure drive and adjustment[C]//34th Chinese Control Conference. Piscataway, USA: IEEE, 2015: 5953-5958.
|
| [26] |
Keithly D, Whitehead J, Voinea A, et al. A cephalopod-inspired combustion powered hydro-jet engine using soft actuators[J]. Extreme Mechanics Letters, 2018, 20. DOI:10.1016/j.eml.2017.11.007 |
| [27] |
Wang S, Huang B, McCoul D, et al. A soft breaststroke-inspired swimming robot actuated by dielectric elastomers[J]. Smart Materials and Structures, 2019, 28(4). DOI:10.1088/1361-665X/ab0a7a |
| [28] |
Christianson C, Bayag C, Li G R, et al. Jellyfish-inspired soft robot driven by fluid electrode dielectric organic robotic actuators[J]. Frontiers in Robotics and AI, 2019, 6: 126. DOI:10.3389/frobt.2019.00126 |
| [29] |
教柳, 张保成, 张开升, 等. 两关节压力驱动柔性仿生机器鱼的设计与仿真[J]. 力学学报, 2020, 52(3): 817-827. Jiao L, Zhang B C, Zhang K S, et al. Design and simulation of two-joint pressure-driven soft bionic fish[J]. Chinese Journal of Theoretical and Applied Mechanics, 2020, 52(3): 817-827. |
| [30] |
Fan J Z, Wang S Q, Yu Q G, et al. Swimming performance of the frog-inspired soft robot[J]. Soft Robotics, 2020, 7(5): 615-626. |
| [31] |
Yang Z Y, Chen D S, Levine D J, et al. Origami-inspired robot that swims via jet propulsion[J]. IEEE Robotics and Automation Letters, 2021, 6(4): 7145-7152. |
 2023, Vol. 45
2023, Vol. 45


