2. 华中科技大学机械科学与工程学院, 湖北 武汉 430074
2. School of Mechanical Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, China
铣削加工过程中存在的颤振现象,是影响铣削质量与效率的重要因素。颤振的发生会增加工件表面的粗糙度,影响加工质量,导致工件报废。保守的工艺参数虽然可以防止颤振的发生,但往往也无法发挥出机械的全部性能,无法让加工效率最大化。因此针对颤振稳定性的研究至关重要。
国内外学者已经进行了很多关于铣削稳定性影响因素的研究。Kaliński等[1]认为减少颤振的方法之一取决于主轴转速的选择,并构建了不同位置点最佳主轴转速的映射图。Zatarain等[2]使用子空间迭代法评估具有不规则螺距的铣刀的加工稳定性。Chao等[3]提出了应用于5轴CNC(数控机床)加工中心的自动调整刀具轴方向的方法,以避免沿刀具路径的颤动。Ozkirimli等[4]提出了一种数值频域铣削稳定性求解方法,在零阶近似法(ZOA)中引入速度平均时间延迟项,通过对特征值问题的迭代求解,实现对各种刀具铣削稳定域的预测。Tunc等[5]分析了过程阻尼的非线性现象,深入研究了过程阻尼对多模式铣削系统的影响,得出了若模态过程阻尼不足,则不能抑制低频模态,从而导致铣削系统不稳定的结论。曹宏瑞等[6]提出了一种考虑变速主轴动态的预测高速铣削颤振稳定性的方法,利用高速主轴系统的动力学模型,通过仿真和实验系统地研究主轴和轴承的速度效应,发现具有速度效应的稳定区域明显向低速区域偏移。李鹏松等[7]考虑一类单自由度的非线性再生型颤振系统,分析时滞参数对稳定性的影响。邓聪颖等[8]提出了一种能够快速评估机床位置相关铣削稳定性的方法。万敏等[9-13]分析了铣削系统的多时滞效应,认为机床加工中的多时滞效应是由刀具跳动效应或螺旋角不均匀引起的。这些文献提出了一个统一的铣削颤振预测模型,证实了使用半离散法求解多时滞效应是有效的。
数控机床虽在铣削稳定性和加工质量上有着更好的表现,但对于大型构件的铣削加工任务,数控机床的成本高昂、灵活性差。铣削机器人则具备可扩展的工作空间,且在同等工作空间下其成本远低于数控机床,为解决大型构件铣削难题提供了新的解决思路。然而,机器人串联构形导致的刚度较弱问题[14]使机器人绝对轨迹精度远低于数控机床,进而引起切削力和过程阻尼变化。在机床加工中可被忽略的轨迹跟踪误差是影响机器人加工质量的关键因素之一,其会对机器人铣削稳定性预测造成明显的影响。目前诸多学者对机器人加工误差、精度补偿和加工工艺等问题开展了研究[15-17]。对机器人铣削颤振的研究主要集中在机器人刚度、机器人动态行为和机器人铣削颤振机制。Tyapin等[18]基于静态模型估算铣削力,并通过少量实验得到各关节刚度。王战玺等[19]认为机器人的低刚度是导致机器人铣削颤振的主要因素之一。Tunc等[20-21]研究了用于机器人铣削的六脚平台的动力学特性,发现其特性在不同的位置下发生变化。李静等[22]使用再生颤振理论分析颤振问题,考虑交叉传递函数并绘制了机器人稳定性Lobe图。郝大贤[23]利用再生颤振理论预测机器人高速铣削稳定域,验证再生颤振理论同样适用于机器人铣削,通过实验发现较短路径下机器人位姿对动态特性的影响很小。在机器人铣削领域,对轨迹跟踪误差的研究主要集中在分析产生轨迹跟踪误差的原因,包括动态切削力引起的关节弹性变形,关节传动机构间隙以及控制迟滞等因素[24]。在此基础上,针对不同原因,提出轨迹跟踪误差的补偿算法与控制策略,提高机器人加工精度[25-28]。但少有学者提及机器人的轨迹精度与机器人加工颤振之间的关系。
本文基于文[23],研究了机器人高速铣削过程中的轨迹精度对加工稳定性的影响。测试了机器人的轨迹跟踪误差;分析了机器人轨迹跟踪精度对动态切削厚度和时滞效应的影响,讨论了轨迹精度与加工过程阻尼系数的关系;建立了考虑机器人轨迹精度的铣削动力学模型,利用改进的半离散方法求解了机器人铣削的稳定域,绘制了稳定性Lobe图;对机器人进行了铣削实验,通过实验验证了理论模型,并对实验中的现象进行了讨论。
2 机器人轨迹跟踪误差实验(Experiment in robot trajectory tracking error)不同于机床的高精度特点,机器人的本体结构导致其轨迹精度较差。研究轨迹精度对加工稳定性的影响,首先需要对机器人进行了轨迹精度实验,以获得机器人轨迹误差的参数。
选择一段较长的轨迹进行实验,分别沿基坐标系的

|
图 1 轨迹跟踪误差实验 Fig.1 Experiment in trajectory tracking error |
设置激光跟踪仪采样频率为1000 Hz,通过PolyWorks软件进行记录。实验中观察得到机器人轨迹波动在3~20 Hz,设计一种带通滤波器,滤除测量过程中的趋势项和高频噪声。带通滤波器的阻带频率为2 Hz时,通带频率为3 Hz。通带频率为20 Hz时,阻带频率为30 Hz。
滤波后,机器人沿
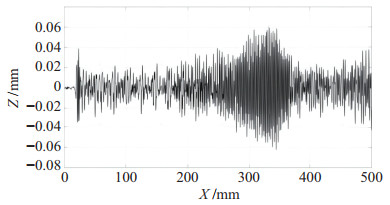
|
图 2 机器人沿X轴运行时TCP点在Z轴方向上的波动 Fig.2 TCP fluctuation in the Z axis direction when the robot runs along the X axis |

|
图 3 机器人沿Y轴运行时TCP点在Z轴方向上的波动 Fig.3 TCP fluctuation in the Z axis direction when the robot runs along the Y axis |
对采集到的信号进行FFT(快速傅里叶变换),如图 4、5所示。当机器人沿
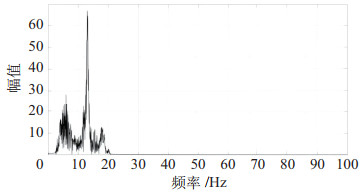
|
图 4 滤波信号沿$X$ 轴的频谱 Fig.4 Spectrum of the filtered signal along the X axis |
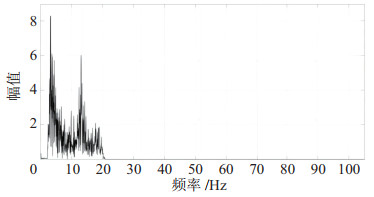
|
图 5 滤波信号沿Y轴的频谱 Fig.5 Spectrum of the filtered signal along the Y axis |
同理采集机器人在
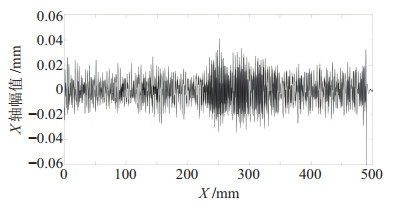
|
图 6 机器人沿Y轴运行时TCP点在X轴方向上的波动 Fig.6 TCP fluctuation in the X axis direction when the robot runs along the Y axis |
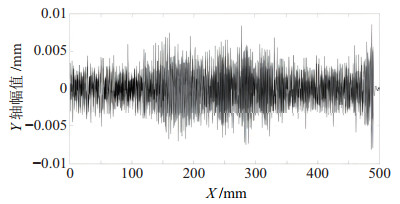
|
图 7 机器人X轴运行时TCP点在Y轴方向上的波动 Fig.7 TCP fluctuation in the Y axis direction when the robot runs along the X axis |
机器人具有较高的轨迹误差会影响切削过程中的动态切削厚度和时滞效应。同时,沿
如图 8所示,

|
图 8 考虑机器人跟踪精度的铣削系统模型 Fig.8 Milling system model considering the robot tracking accuracy |
将轨迹跟踪误差近似为周期为
| $ \begin{align} \begin{cases} x_{0{\rm er}} =V_{\rm f}\; t+e_{x} \sin (\omega_{{\rm e}x} t+\theta_{x}) \\ y_{0{\rm er}} =e_{y} \sin (\omega_{{\rm e}y} t+\theta_{y}) \end{cases} \end{align} $ | (1) |
其中,
| $ \begin{align} h(\phi_{j})\approx \, & \big(x(t-\tau)-x(t)\big)\sin \phi_{j} (t)+ \\ & \big(e_{x} \sin \left(\omega_{{\rm e}x} (t-\tau)+\theta_{x}\right)- \\ & e_{x} \sin (\omega_{{\rm e}x} t+\theta_{x})\big)\sin \phi_{j} (t)+ \\ & \big(y(t-\tau)-y(t)\big)\cos \phi_{j} (t) \end{align} $ | (2) |
其中,
实验中系统轨迹误差周期函数属于低频位移波动,观察到的波动周期通常在20 Hz以内,一般情况下频率远低于铣刀切削频率,则最大时滞周期
| $ \begin{align} N_{\rm m} =[ T_{\rm er} /\tau ] \end{align} $ | (3) |
其中,
| $ \begin{align} \begin{cases} F_{x, j} =-F_{{\rm t}j} \cos \phi_{j} -F_{{\rm r}j} \sin \phi_{j} \\ F_{y, j} =+F_{{\rm t}j} \sin \phi_{j} -F_{{\rm r}j} \cos \phi_{j} \end{cases} \end{align} $ | (4) |
其中,
考虑多时滞效应影响的动态铣削力模型为
| $ \begin{align} {\mathit{\boldsymbol{F}}}(t) & =\begin{pmatrix} F_{x} (t) \\ F_{y} (t) \end{pmatrix}=\frac{1}{2}aK_{\rm t} \sum\limits_{l=1}^{N_{\rm m}} \mathit{\boldsymbol{H}}_{l} (t) \mathit{\boldsymbol{\varDelta}}_{\text{sum}} (t) \\[-8pt]\; \end{align} $ | (5) |
| $ \begin{align} \mathit{\boldsymbol{H}}_{l} (t) & = \begin{bmatrix} h_{l, xx} & h_{l, xy} & h_{l, x\:{\rm er}} \\ h_{l, yx} & h_{l, yy} & h_{l, y\:{\rm er}} \end{bmatrix} \end{align} $ | (6) |
其中
| $ \begin{equation} \begin{aligned} h_{l, xx} & =\sum _{j=0}^{N-1} -g_{l, j} \left[ \sin 2\phi_{j} +K_{\rm r} (1-\cos 2\phi_{j})\right] \\ h_{l, xy} & =\sum _{j=0}^{N-1} -g_{l, j} \left[ (1+\cos 2\phi_{j})+K_{\rm r} \sin 2\phi_{j}\right] \\ h_{l, yx} & =\sum _{j=0}^{N-1} g_{l, j} \left[ (1-\cos 2\phi_{j})-K_{\rm r} \sin 2\phi_{j}\right] \\ h_{l, yy} & =\sum _{j=0}^{N-1} g_{l, j} \left[ \sin 2\phi_{j} -K_{\rm r} (1+\cos 2\phi_{j})\right] \\ h_{l, x\:{\rm er}} & =\sum _{j=0}^{N-1} -g_{l, j} \left[ \sin 2\phi_{j} +K_{\rm r} (1-\cos 2\phi_{j})\right] \\ h_{l, y\:{\rm er}} & =\sum _{j=0}^{N-1} -g_{l, j} \left[ \sin 2\phi_{j} +K_{\rm r} (1-\cos 2\phi_{j})\right] \end{aligned} \end{equation} $ | (7) |
其中,
将过程阻尼因素引入系统模型需要确定过程阻尼系数。本文利用Budak等[30-31] 提出的一种实用的过程阻尼辨识方法,通过公式估计系统阻尼系数。
| $ \begin{align} c^{\rm p}=\frac{K_{\rm d} I}{A\pi} \end{align} $ | (8) |
其中,
将过程阻尼的影响考虑在内后,式(5) 转换为
| $ \begin{align} \mathit{\boldsymbol{F}}(t) & =\frac{1}{2}aK_{\rm t} \sum _{l=1}^{N_{\rm m}} \mathit{\boldsymbol{H}}_{l} (t)\mathit{\boldsymbol{\varDelta}}_{\text{sum}} (t) -\mathit{\boldsymbol{c}}_{\rm p} \mathit{\boldsymbol{\dot{q}}}(t) \end{align} $ | (9) |
| $ \begin{align} \mathit{\boldsymbol{c}}_{\rm p} & = \begin{bmatrix} c_{x}^{\rm p} & \\ & c_{y}^{\rm p} \end{bmatrix} \end{align} $ | (10) |
其中,
根据已知的
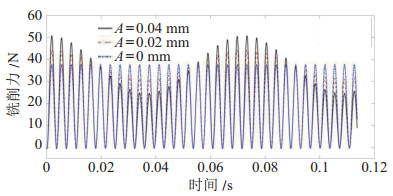
|
图 9 考虑机器人轨迹跟踪误差时的铣削力仿真结果 Fig.9 Simulation results for the milling force considering the robot trajectory tracking error |
当误差波动幅值
针对机器人铣削系统,建议如下的动力学微分方程:[32-33]
| $ \begin{align} &\mathit{\boldsymbol{M\ddot{q}}}(t)+( \mathit{\boldsymbol{C}}+\mathit{\boldsymbol{c}}_{\rm p} )\mathit{\boldsymbol{\dot{q}}}(t)+\mathit{\boldsymbol{Kq}}(t)\\ =&\frac{1}{2}aK_{\rm t} \sum _{l=1}^{N_{\rm m}} \mathit{\boldsymbol{H}}_{l} (t)\mathit{\boldsymbol{\varDelta}}_{\text{sum}} (t) \end{align} $ | (11) |
其中,
如图 10所示,改进的模型中加入了机器人轨迹跟踪误差
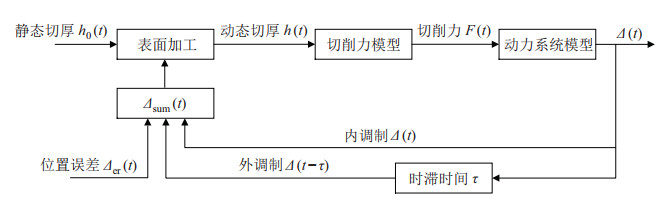
|
图 10 考虑位移误差时的再生颤振动力学模型方框图 Fig.10 Block diagram of the regenerative chatter dynamics model considering the displacement error |
因此,在将轨迹跟踪误差导致的位移近似表示为周期函数的形式后,系统动力学模型可以转化为多时滞动力系统模型,进而在考虑轨迹跟踪误差条件下进行铣削稳定性预测。本文将使用改进的半离散法分析延迟数大于1的多时滞系统[10]。
3.3 稳定性分析首先需要获得铣削系统的FRF(频率响应函数)。使用单轴加速度计,对刀尖点进行锤击实验,具体实施方法参考文[22]。基于LabVIEW平台设计开发了一套集采集、分析于一体的软件,采集加速度和力锤信号,对模态实验数据进行处理后得到系统的FRF函数。通过Levy法辨识机器人铣削系统的模态参数,得到拟合FRF曲线,并将模态参数代入到模型中,分析系统的稳定性。其操作界面如图 11所示。
|
图 11 软件操作界面 Fig.11 Software operation interface |
为了获得机器人铣削的稳定性Lobe图,首先规划机器人的铣削路径,获得加工路径上的轨迹误差数据。设计一段沿机器人基坐标系的
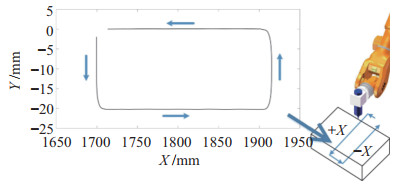
|
图 12 X-Y平面上机器人加工轨迹 Fig.12 Processing trajectory of the robot on X-Y plane |
实验得到系统参数后将参数代入改进模型中。利用半离散法分析系统稳定性,选择误差波动幅值为0 mm、0.02 mm和0.04 mm三种不同的情况,绘制系统的稳定性Lobe图,如图 13所示。从图中可以看出,系统的误差波动幅值越大,系统的稳定域就越大。
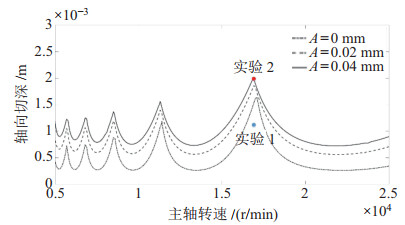
|
图 13 不同轨迹跟踪误差下的稳定性Lobe图 Fig.13 Lobe diagram of the stability under different trajectory tracking errors |
根据仿真得到稳定性Lobe图后,将通过铣削实验,验证新模型的可行性。
4.1 实验设计选择2组实验参数进行实验,如表 1所示。
|
|
表 1 铣削参数 Tab. 1 Milling parameters |
如图 13所示,选择实验2中所列铣削参数,在
根据确定的2组试验参数,进行铣削实验,改变工件位置保证2组实验中机器人的运动轨迹一致,如图 14所示。在机器人手腕末端固定连接一个安装座,靶球与加速度计固定在安装座上。在铣削过程中,通过激光跟踪仪采集加工过程中机器人手腕处的位移数据,三轴加速度计采集铣削过程中的加速度信号,麦克风采集铣削过程中的声振信号。2次槽铣加工后的铣削效果如图 15所示。

|
图 14 机器人铣削实验系统 Fig.14 Robotic milling experiment system |

|
图 15 X-Y平面槽铣结果 Fig.15 Slot milling results on X-Y plane |
对加工过程中采集到的振动与位移信号进行分析,发现了一些与传统机床加工领域不同的特殊情况。
对采集的铣削轨迹沿
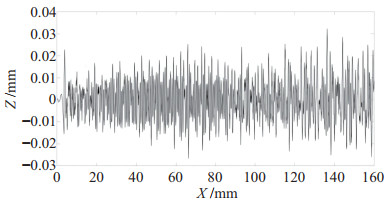
|
图 16 沿+X方向铣削时Z方向的位移波动 Fig.16 Displacement fluctuation in Z direction when milling along +X direction |
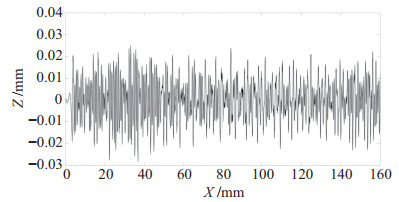
|
图 17 沿-X方向铣削时Z方向的位移波动 Fig.17 Displacement fluctuation in Z direction when milling along -X direction |
实验1:沿
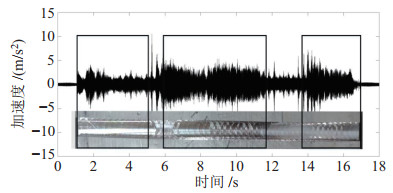
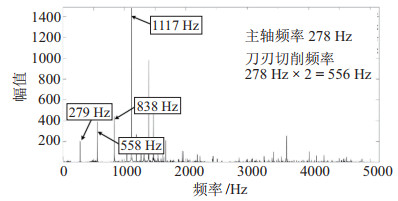
在实验1中,加工过程中加速度计的时域信号与其对应的加工路径效果如图 18、19所示。对加速度计的时域信号进行FFT变换,得到加工过程中的频谱图,如图 20所示。其频谱在
|
图 18 实验1中沿+X方向的加速度计信号与铣削结果 Fig.18 Accelerometer signal and milling result along +X direction in test 1 |

|
图 19 实验1中沿-X方向的加速度计信号与铣削结果 Fig.19 Accelerometer signal and milling result along -X direction in test 1 |
|
图 20 实验1中的加速度信号频谱图(+X、-X方向结果基本相同) Fig.20 The frequency spectrum of the acceleration signal in test 1 (the results are basically the same in +X and -X directions) |
从加速度计频谱图可以看出,在切深为1 mm时,整个加工过程都是稳定的,没有出现颤振频率。
在实验中,机器人沿
造成这种现象的原因可能是由于引入了轨迹误差后,铣削过程中动态切削厚度的最大值增大,加工过程中的最大切削力也相应增大。这与3.1节中图 9的时域仿真结果相一致。在加速度计时域信号上的表现为加速度幅值相应增大。
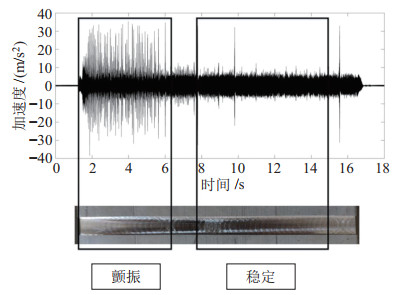
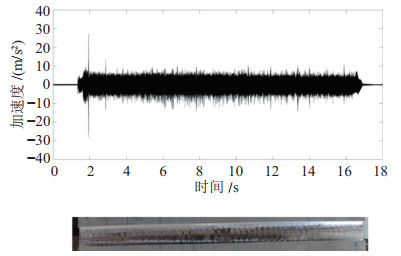
实验2:沿
|
图 21 实验2中沿+X方向的加速度计信号与铣削结果 Fig.21 Accelerometer signal and milling result along +X direction in test 2 |
|
图 22 实验2中沿-X方向的加速度计信号与铣削结果 Fig.22 Accelerometer signal and milling result along -X direction in test 2 |
对加速度计的时域信号按照颤振部分和稳定部分进行FFT变换,得到实验2加工过程的频谱图,如图 23、24所示。
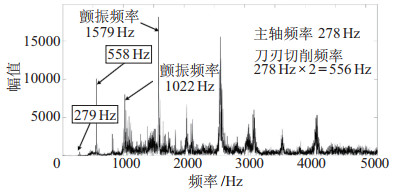
|
图 23 实验2中系统沿+X方向的颤振部分频谱图 Fig.23 Spectrogram of the flutter part in the system along the +X direction in test 2 |
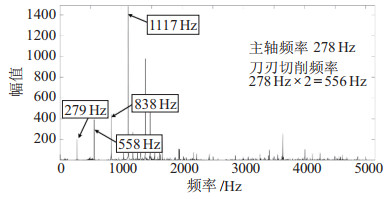
|
图 24 实验2中稳定铣削部分的频谱图 Fig.24 Spectrogram of the stable milling part in test 2 |
图 23为实验2中颤振部分的频谱图,可以明显发现不属于刀具通过频率及其倍频的颤振频率,且颤振频率的幅值最大。说明加工过程中发生了明显的颤振。实验2中稳定加工部分的频谱如图 24所示,没有出现颤振频率。其中稳定加工频谱图中幅值最大的振动频率1117 Hz与1396 Hz均为铣刀刀刃通过频率的倍频。
机器人在沿
这种现象说明加工过程中的颤振稳定性与加工路径相关。引入轨迹误差波动后的改进模型可以解释这种现象,同时该现象也与机器人位姿改变而引起的模态变化相关。机器人轨迹跟踪误差会影响加工过程中的临界稳定切深,如图 13所示。从图 16、17可以分析得出,沿
虽然机器人的精度误差会扩大铣削过程中的稳定域,但其是否存在一定的适用范围还需要进一步讨论。而且从实验中采集的数据看,当轨迹误差较大时,表面的刀痕也较明显,被加工零件表面质量并没有得到提高。所以被加工工件表面的粗糙度不能成为判断机器人加工过程中是否发生颤振的直接依据。是否使用机器人轨迹跟踪误差来抑制机器人铣削加工过程中的再生颤振还需要进一步讨论。
5 结论(Conclusion)1) 建立了考虑轨迹精度误差的动态切削力和机器人铣削系统动力学模型。机器人的轨迹跟踪误差影响切削过程中的动态切削厚度和时滞效应,进而影响了再生效应中的反馈调制环节,抑制了再生颤振的发生。
2) 较高的机器人轨迹跟踪误差会引起刀具与被加工工件的底面发生划擦,为机器人加工过程提供更多的过程阻尼,进一步提高了稳定域。但同时也会造成表面质量与尺寸精度的下降。
3) 通过铣削实验,发现了机器人轨迹跟踪误差对颤振稳定性的影响规律。在铣削过程中,轨迹跟踪误差的波动影响了加工中的临界轴向切深,导致机器人铣削系统在某些加工路径上出现颤振发生又逐渐消失的特殊现象。
通过上述研究,阐释了机器人铣削加工中的颤振机理,指出了机器人与机床加工的区别。本文研究内容为抑制机器人铣削颤振提供了新的理论模型,同时可为大去除量的加工应用和高效加工应用提供工艺参数选择指导,提高机器人铣削加工效率。
| [1] |
Kaliński K J, Mazur M, Galewski M A. The optimal spindle speed map for reduction of chatter vibration during milling of bow thruster blade[J]. Solid State Phenomena, 2013, 198: 686-691. DOI:10.4028/www.scientific.net/SSP.198.686 |
| [2] |
Zatarain M, Dombovari Z. Stability analysis of milling with irregular pitch tools by the implicit subspace iteration method[J]. International Journal of Dynamics and Control, 2014, 2: 26-34. DOI:10.1007/s40435-013-0052-7 |
| [3] |
Chao S, Altintas Y. Chatter free tool orientations in 5-axis ball-end milling[J]. International Journal of Machine Tools and Manufacture, 2016, 106: 89-97. DOI:10.1016/j.ijmachtools.2016.04.007 |
| [4] |
Ozkirimli O, Tunc L T, Budak E. Generalized model for dynamics and stability of multi-axis milling with complex tool geometries[J]. Journal of Materials Processing Technology, 2016, 238: 446-458. DOI:10.1016/j.jmatprotec.2016.07.020 |
| [5] |
Tunc L T, Mohammadi Y, Budak E. Destabilizing effect of low frequency modes on process damped stability of multi-mode milling systems[J]. Mechanical Systems and Signal Processing, 2018, 111: 423-441. DOI:10.1016/j.ymssp.2018.03.051 |
| [6] |
Cao H R, Li B, He Z J. Chatter stability of milling with speed-varying dynamics of spindles[J]. International Journal of Machine Tools and Manufacture, 2011, 52(1): 50-58. |
| [7] |
李鹏松, 盛桂全, 孟永永. 再生型颤振系统的Hopf分岔分析与控制[J]. 吉林大学学报(理学版), 2014, 52(6): 1155-1161. Li P S, Sheng G Q, Meng Y Y. Analysis and control of Hopf bifurcation for regenerative chatter system[J]. Journal of Jilin University (Science Edition), 2014, 52(6): 1155-1161. |
| [8] |
Deng C Y, Miao J G, Wei B, et al. Evaluation of machine tools with position-dependent milling stability based on Kriging model[J]. International Journal of Machine Tools and Manufacture, 2018, 124: 33-42. DOI:10.1016/j.ijmachtools.2017.09.004 |
| [9] |
Ma Y C, Wan M, Zhang W H. Effect of cutter runout on chatter stability of milling process[J]. Procedia CIRP, 2016, 56: 115-118. DOI:10.1016/j.procir.2016.10.034 |
| [10] |
Wan M, Zhang W H, Dang J W, et al. A unified stability prediction method for milling process with multiple delays[J]. International Journal of Machine Tools and Manufacture, 2010, 50(1): 29-41. DOI:10.1016/j.ijmachtools.2009.09.009 |
| [11] |
Wan M, Lu M S, Zhang W H, et al. A new ternary-mechanism model for the prediction of cutting forces in flat end milling[J]. International Journal of Machine Tools and Manufacture, 2012, 57: 34-45. DOI:10.1016/j.ijmachtools.2012.02.003 |
| [12] |
Wan M, Wang Y T, Zhang W H, et al. Prediction of chatter stability for multiple-delay milling system under different cutting force models[J]. International Journal of Machine Tools and Manufacture, 2011, 51(4): 281-295. DOI:10.1016/j.ijmachtools.2010.12.007 |
| [13] |
卢晓红, 王凤晨, 王华, 等. 铣削过程颤振稳定性分析的研究进展[J]. 振动与冲击, 2016, 35(1): 74-82. Lu X H, Wang F C, Wang H, et al. Review about chatter stability analysis in milling process[J]. Journal of Vibration and Shock, 2016, 35(1): 74-82. |
| [14] |
刘辛军, 谢福贵, 汪劲松. 当前中国机构学面临的机遇[J]. 机械工程学报, 2015, 51(13): 2-12. Liu X J, Xie F G, Wang J S. Current opportunities in the field of mechanisms in China[J]. Journal of Mechanical Engineering, 2015, 51(13): 2-12. |
| [15] |
李文龙, 谢核, 尹周平, 等. 机器人加工几何误差建模研究: Ⅰ空间运动链与误差传递[J]. 机械工程学报, 2021, 57(7): 154-168. Li W L, Xie H, Yin Z P, et al. The research of geometric error modeling of robotic machining: I Spatial motion chain and error transmission[J]. Journal of Mechanical Engineering, 2021, 57(7): 154-168. |
| [16] |
郝大贤, 王伟, 王琦珑, 等. 复合材料加工领域机器人的应用与发展趋势[J]. 机械工程学报, 2019, 55(3): 1-17. Hao D X, Wang W, Wang Q L, et al. Applications and development trend of robotics in composite material process[J]. Journal of Mechanical Engineering, 2019, 55(3): 1-17. |
| [17] |
陈钦韬, 殷参, 张加波, 等. 面向铣削任务的工业机器人刚度位姿优化[J]. 机器人, 2021, 43(1): 90-100. Chen Q T, Yin S, Zhang J B, et al. Pose optimization of industrial robots based on stiffness for milling tasks[J]. Robot, 2021, 43(1): 90-100. |
| [18] |
Tyapin I, Kaldestad K B, Hovland G. Off-line path correction of robotic face milling using static tool force and robot stiffness[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2015: 5506-5511.
|
| [19] |
王战玺, 张晓宇, 李飞飞, 等. 机器人加工系统及其切削颤振问题研究进展[J]. 振动与冲击, 2017, 36(14): 147-155, 188. Wang Z X, Zhang X Y, Li F F, et al. Review on the research developments of robot machining systems and cutting chatter behaviors[J]. Journal of Vibration and Shock, 2017, 36(14): 147-155, 188. |
| [20] |
Tunc L T, Shaw J. Experimental study on investigation of dynamics of hexapod robot for mobile machining[J]. The International Journal of Advanced Manufacturing Technology, 2016, 84(5-8): 817-830. |
| [21] |
Tunc L T, Stoddart D. Tool path pattern and feed direction selection in robotic milling for increased chatter-free material removal rate[J]. The International Journal of Advanced Manufacturing Technology, 2017, 89(9-12): 2907-2918. |
| [22] |
Li J, Li B, Shen N Y, et al. Effect of the cutter path and the workpiece clamping position on the stability of the robotic milling system[J]. The International Journal of Advanced Manufacturing Technology, 2016, 89(9-12): 2919-2933. |
| [23] |
Hao D X, Wang W, Liu Z, et al. Experimental study of stability prediction for high-speed robotic milling of aluminum[J]. Journal of Vibration and Control, 2019, 26(7-8): 387-398. |
| [24] |
Yang T F, Yan S Z, Han Z Y. Nonlinear model of space manipulator joint considering time-variant stiffness and backlash[J]. Journal of Sound and Vibration, 2015, 341: 246-259. |
| [25] |
文科, 张加波, 乐毅, 等. 数控驱动的移动铣削机器人精度提升方法[J]. 机械工程学报, 2021, 57(5): 72-80. Wen K, Zhang J B, Yue Y, et al. Method for improving accuracy of NC-driven mobile milling robot[J]. Journal of Mechanical Engineering, 2021, 57(5): 72-80. |
| [26] |
Petko M, Karpiel G, Gac K, et al. Trajectory tracking controller of the hybrid robot for milling[J]. Mechatronics, 2016, 37: 100-111. |
| [27] |
Olabi A, Béarée R, Gibaru O, et al. Feedrate planning for machining with industrial six-axis robots[J]. Control Engineering Practice, 2010, 18(5): 471-482. |
| [28] |
Qian M R, Jiang J. Robust adaptive iterative learning control for trajectory tracking of uncertain robotic systems[C]//Chinese Automation Congress. Piscataway, USA: IEEE, 2018: 1896-1902.
|
| [29] |
Jiang S L, Sun Y W. A multi-order method for predicting stability of a multi-delay milling system considering helix angle and run-out effects[J]. Chinese Journal of Aeronautics, 2018, 31(6): 1375-1387. |
| [30] |
Budak E, Tunc L T. A new method for identification and modeling of process damping in machining[J]. Journal of Manufacturing Science and Engineering, 2009, 131(5). DOI:10.1115/1.4000170 |
| [31] |
Tuysuz O, Altintas Y. Analytical modeling of process damping in machining[J]. Journal of Manufacturing Science and Engineering, 2019, 141(6). DOI:10.1115/1.4043310 |
| [32] |
Niu J B, Ding Y, Zhu L M, et al. Mechanics and multi-regenerative stability of variable pitch and variable helix milling tools considering runout[J]. International Journal of Machine Tools and Manufacture, 2017, 123: 129-145. |
| [33] |
Insperger T, Stepan G. Updated semi-discretization method for periodic delay-differential equations with discrete delay[J]. International Journal for Numerical Methods in Engineering, 2004, 61(1): 117-141. |
 2023, Vol. 45
2023, Vol. 45


