海洋观测船是搭载科学仪器设备执行海洋探测任务的最常用的一类观测平台,具有自持力强、作业时间长、观测范围广等特点。海洋观测船在风浪作用下产生摆荡,严重影响其搭载的观测仪器的测量精度。虽然船体对设备的运动扰动是6自由度的,然而在很多场景下平移扰动可通过后期处理完成数据校正(如多波束测深)或依靠姿态调节抵消影响(如火炮稳定),因此姿态稳定平台具有较广泛的用途。姿态稳定平台通常由3转动自由度机构构成,固定安装于船舶与仪器之间,通过实时调整主动关节输入变量,大幅提升船载设备的姿态稳定性,是仪器姿态随船变动问题的有效解决方案。
与串联机构相比,并联机构具有高刚度、高动态特性、高功率密度等特点[1],非常适于在船上局促空间内搭载测量仪器与设备,并补偿其动态变化的姿态角。在机构构形确定的前提下,运动学参数优化是提升机构运动性能的有效手段[2]。对于3转动自由度船载并联稳定平台,在开展其运动学参数优化设计时,需要着重考虑如下两方面因素:1) 在机构主尺度已给定的情况下,如何设计得到较大的工作空间,即较大的姿态角调节范围,以提升船载稳定平台在恶劣海况下的作业能力;2) 在主动关节驱动力(驱动功率)受限的情况下,如何改善机构在全工作空间内的力传递性能,以提升稳定平台的负载能力以及对复杂海况的动态响应能力。
并联运动平台工作空间分析与优化的关键在于建立机构尺度参数、关节约束与动平台位姿实现能力之间的映射关系。在早期研究中,学者们多利用几何法计算工作空间。Gosselin[3]运用圆弧相交法,对3-RPR并联机构进行了工作空间分析。为使求解更快捷,Aboulissane等[4]提出利用CAD(计算机辅助设计)软件进行工作空间的辅助求解。然而,几何法缺乏通用性,且当约束条件增多时解算困难,因此机构工作空间的数值求解法也被广泛研究。Castelli等[5]提出了一种基于离散化方法确定工作空间边界、体积和形状指数的算法。与之类似的还有蒙特卡洛法[6],将关节空间离散化,并通过正运动学搜索出机构的工作空间。此类方法只需机构运动学正逆解模型,其余工作均可由程序进行迭代求解,流程简便且适用性强。此外还有一些改进的求解法。Bohigas等[7]提出了分枝剪枝技术,该技术可以确定一般低自由度串联或并联机构的所有工作空间边界点。Rouhani等[8]考虑多种约束,利用改进的自适应步长法对工作空间作离散化和求解。相比较而言,离散化搜索空间边界的数值法更简便适用,能快速完成工作空间的求解。
船载稳定平台的载荷能力也是其重要运动性能,可用力传递率指标对其作评价。力传递率代表了机构支链驱动力转换为平台输出力/力矩的能力,在很多文献中也称为“可操作性”。张新[9]将该性能称为“承载力性能”,并采用雅可比矩阵的最小奇异值作为评价指标,而且从数学机理上说明了其合理性。Chen等[10]提出了一个传递指标来评估并联机械手的力和扭矩传递质量,该指标可被归一化并用于分析精确约束的并联机械手。除分析力与力间的联系外,也有学者直接分析运动与力之间的传递关系,同样可应用于平台载荷能力的评价。刘辛军等[11]基于传动角概念提出了并联机构运动/力传递率评价指标,为机构的优化设计提供了一种有效的手段。Wu等[12]使用虚拟传动系数指标对运动/力传递性能进行评价,而Liu等[13]基于最大虚系数的双重属性定义了一种评价力传递性能的新指标,其优势在于可更精细地识别机构运动学性能。由于稳定平台实际应用过程中载荷不确定,因此在设计阶段考虑力与力间的传递性能更为恰当。上述评价指标均是局部力传递率,随机构位形变化而变化,为评价整个工作空间的性能,需要进一步考虑全域力传递能力指标。刘海涛等[14]采用局部指标的全域平均值作为整体性能指标;叶伟等[15]从优质空间考虑,提出了采用优质传递空间与整体传递空间的比值评价整体传力性能的方法。然而后者适用于对某确定的机构进行运动性能分析,对于构形优化而言,前者可以提供全域性能绝对值,因此更为合适。
并联机构的尺度优化设计通常可以转化为以尺度参数为设计变量,以单一或综合性能指标最优为目标,并综合考虑工程约束的优化问题。叶伟等[15]在设计空间内采用性能图谱法求解出性能较好的区域,但此方法难以精确求出最优参数。为准确地找出最优参数解,较多学者从优化问题中凝练出目标函数,采用最值函数[16]或遗传算法[17-18]等来完成综合指标的优化求解。程元皓等[19]采用改进非支配排序遗传算法完成了多目标优化求解,与普通算法相比,改进后的算法具有更高的求解精度和效率。
本文以3-UPS & S并联船载姿态稳定平台为对象,重点结合应用场景的实际需求,以工作空间和力传递性能为优化目标,采用改进的自适应小生境遗传算法完成对尺度参数的优化设计,并通过与初始构形的性能对比以及样机实验结果,验证了所做优化设计的有效性。
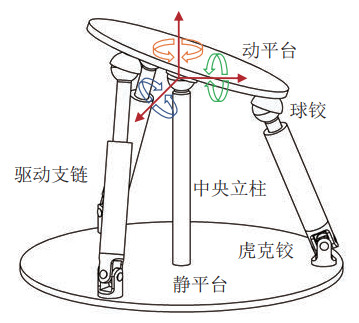
2 机构描述(Mechanism description)3-UPS & S船载并联稳定平台的结构简图如图 1所示。该机构由与船体固定连接的静平台、搭载观测设备的动平台、与两者相连的3条UPS支链以及中央立柱组成。在此,U、P、S分别表示虎克铰、移动副以及球铰,P表示主动移动副。
|
图 1 3-UPS & S机构 Fig.1 3-UPS & S mechanism |
机构中的UPS支链一端通过虎克铰与静平台连接,另一端通过球铰与动平台相连;中央立柱一端与静平台固定连接,另一端通过球铰与动平台中心相连。中央立柱限制了动平台的三向平动,通过控制3条UPS支链的伸缩量,即可实现动平台3个转动自由度的运动。
如图 2所示,令点

|
图 2 机构坐标系 Fig.2 Mechanism coordinate system |
考虑到该船载稳定平台的应用需求,系
| $ \begin{align*} \boldsymbol{R}=\boldsymbol{R}(z, \phi)\boldsymbol{R}(y, \theta)\boldsymbol{R} (z, \psi -\phi)= (\boldsymbol{u} \; \; \boldsymbol{v} \; \; \boldsymbol{w} ) \end{align*} $ |
式中,
记静平台、动平台铰点所构成三角形的外接圆半径分别为
首先研究3-UPS & S机构的工作空间分析方法,为后文的优化设计奠定基础。
3.1.1 约束条件机构在运动中受到多种约束,可达空间的边界通常是约束条件起作用的点集。
1) 支链杆长约束
支链的长度不能超出杆长允许范围,相应的约束条件可表示为
| $ \begin{align} \begin{cases} l_{\min} <l_{i} <l_{\max} \\ l_{\min} =\sqrt{a^{2}+h^{2}}-b \\ l_{\max} =2l_{\min} \end{cases}, \qquad i=1, 2, 3 \end{align} $ | (1) |
式中,
支链杆长由运动学逆解求得,即
| $ \begin{align} l_{i} =\left\| \overrightarrow {A_{i} B_{i}} \right\|=\left\| h\boldsymbol{k}+\boldsymbol{Rb}_{i} -\boldsymbol{a}_{i} \right\| \end{align} $ | (2) |
式中,
| $ \begin{align*} \boldsymbol{a}_{i} = \begin{pmatrix} a\cos \alpha_{i} \\ a\sin \alpha_{i} \\ 0 \end{pmatrix}, \quad \boldsymbol{b}_{i} = \begin{pmatrix} b\cos \alpha_{i} \\ b\sin \alpha_{i} \\ 0 \end{pmatrix}, \quad \boldsymbol{k}= \begin{pmatrix} 0 \\ 0 \\ 1 \end{pmatrix} \end{align*} $ |
2) 杆间干涉约束
支链与支链、支链与中央立柱之间不能发生接触,约束条件可表示为
| $ \begin{align} d_{\min} >2r_{\text{limb}} \end{align} $ | (3) |
式中,
两支链之间最短距离的计算等价于空间中两线段之间最小距离的求解。依据文[20],可计算两支链间的最短距离。
3) 关节转角约束
关节转动幅度不能超过该关节转角的最大允许值。关节转角约束与铰链的实际设计有关,本文依据设计经验选定球铰和虎克铰的最大允许转角均为
关节基向量的方向与铰链的安装方位有关,合理的铰链安装方位有利于最大程度地发挥铰链的运动能力(偏转范围)。本文在设计支链虎克铰近架轴线的安装方位时,首先依据其他3类约束搜索机构可达工作空间,并同时记录所关注的铰链随动向量的变动范围,最后选取所述范围的“中心方向”作为基准向量,据此设计虎克铰的安装方位。
4) 奇异位形约束
机构处于奇异位形时,其运动可能出现不可控或卡死现象,因此工作空间的选取应当尽量避开奇异位形。雅可比代数法是研究并联机构奇异问题的常用方法[21],对于本文所研究机构,雅可比矩阵
| $ \begin{align} \boldsymbol{J} =\begin{bmatrix} \left(\boldsymbol{Rb}_{1} \times \hat{\boldsymbol{s}}_{1}\right)^{\rm T} \\ \left(\boldsymbol{Rb}_{2} \times \hat{\boldsymbol{s}}_{2}\right)^{\rm T} \\ \left(\boldsymbol{Rb}_{3} \times \hat{\boldsymbol{s}}_{3}\right)^{\rm T} \end{bmatrix}^{-1} \end{align} $ | (4) |
式中,
当雅可比矩阵不满秩,即
采用数值法搜索求解机构的可达空间。具体地,依序给定某位形,判断其是否满足前述4类约束条件,若满足,则该位形属于可达空间;若不满足,则排除该位形。获得机构的可达空间后,再根据船载稳定平台的转角设计需求,从中筛选出机构的工作空间。
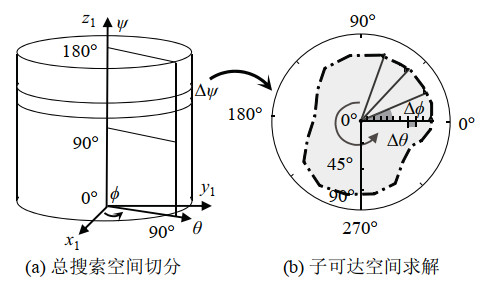
考虑到船载稳定平台的应用场景及机构可达空间关于扭转角的对称性,设定搜索范围为扭转角
|
图 3 可达空间求解示意图 Fig.3 Schematic diagram of reachable space solution |
求得机构可达空间后,需根据船载稳定平台的姿态角设计指标进一步确定其工作空间。在5级海况内,各类舰船的摇摆幅度(RPY角)通常不超过
为综合考量动平台三向转角的取值范围,选用工作空间的体积作为评价指标。依据上述定义,工作空间为圆柱体,且体积可表示为
| $ \begin{align} V=\pi \theta_{\rm d}^{2} ( \psi_{\max} -\psi_{\min}) \end{align} $ | (5) |
式中,
本文定义的力传递率反映了支链驱动力转化为动平台输出力的能力。支链驱动功率一定时,力传递率高表明平台具有更强的负载与动态响应能力。
力传递率有局部与全域之分,其中局部力传递率(LTI)受机构的尺寸比例和位形的共同影响。定义支链输入力矢量
| $ \begin{align} \boldsymbol{F}=\boldsymbol{GF}_{\text{in}} \end{align} $ | (6) |
其中,
| $ \begin{align} \boldsymbol{G}=\boldsymbol{J}^{\rm -T} \end{align} $ | (7) |
局部力传递率评价指标
| $ \begin{align} \eta =| {F_{i}} |_{\min} =\sqrt{\lambda_{\min} ({{\boldsymbol{G}}^{\rm T}{\boldsymbol{G}}})} \end{align} $ | (8) |
式中,
局部力传递率随稳定平台位形变化,为对机构的力传递率做出整体性评价,定义全域力传递率(GTI)为局部力传递率的全域平均值:
| $ \begin{align} \overline{\eta} =\int \eta {\rm d} V /V \end{align} $ | (9) |
式中,
根据文[23],将机构的初始参数比例关系确定为
求解得到实例构形下稳定平台的工作空间体积
|
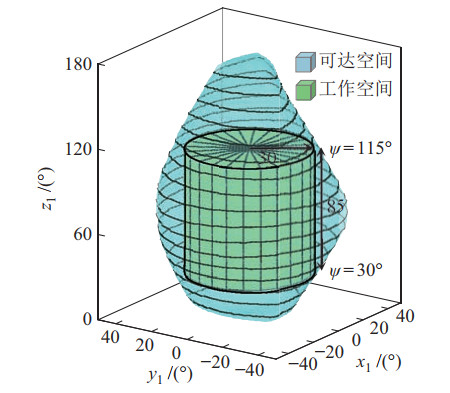
图 4 实例构形的工作空间 Fig.4 Workspace of the example configuration |
外围蓝色区域为机构的可达空间,内部绿色圆柱区域为满足工程需求的工作空间。扭转角
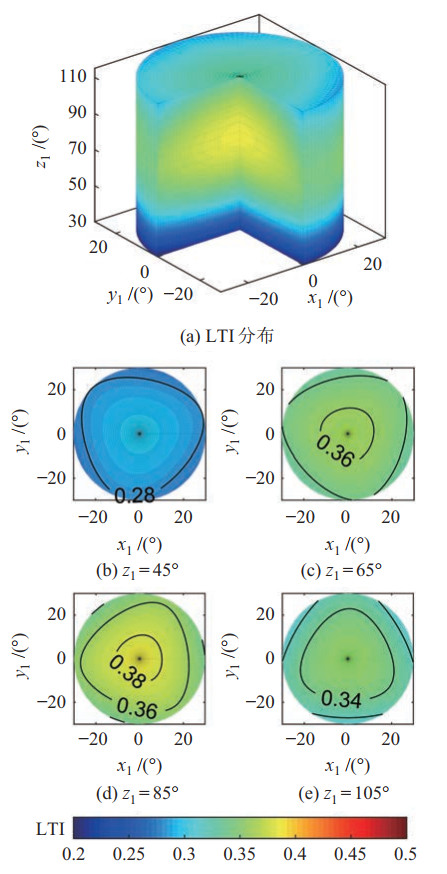
在工作空间范围内,3-UPS & S机构的局部力传递率指标
|
图 5 实例构形的局部力传递率 Fig.5 Local force transmission rate of the example configuration |
由图 5可知,在机构零位对应的扭转角下,力传递性能最好;在扭转角
以工作空间与力传递率综合性能最优为目标构建机构尺度参数优化问题,并采用遗传算法实现优化问题的求解。
4.1 基于性能驱动的优化问题构建 4.1.1 参数设计空间如前所述,稳定平台尺度参数优化的对象是静平台半径
| $ \begin{align} r_{1} =\dfrac{b}{D}, \quad r_{2} =\dfrac{a}{D}, \quad r_{3} =\dfrac{h}{D}, \quad D=\dfrac{a+b+h}{3} \end{align} $ | (10) |
考虑到机构的动态特性以及实际使用需求,动平台半径应小于静平台,即
| $ \begin{align} \varOmega =\, & \big\{(r_{1}, r_{2}, r_{3})\big|r_{1} +r_{2} +r_{3} =3; \\ & \; \; 0<r_{1}, r_{2}, r_{3} <3;r_{1} -r_{2} <0\big\} \end{align} $ | (11) |
依据船载姿态稳定平台的工程需求,以机构工作空间性能与力传递性能的综合最优为目标开展尺寸优化。针对该多目标优化问题,首先对两类指标进行归一化处理,定义如下:
| $ \begin{align} \begin{cases} g_{1} (\boldsymbol{r})=\dfrac{V(\boldsymbol{r})-V_{\min}} {V_{\max} -V_{\min}} \\[6pt] g_{2} (\boldsymbol{r})=\dfrac{\overline{\eta} (\boldsymbol{r})-\overline{\eta}_{\min}} {\overline{\eta}_{\max} -\overline{\eta}_{\min}} \end{cases} \end{align} $ | (12) |
式中,
为满足船载设备姿态稳定的应用场景需求,根据5级海况下各型船舶的摇摆幅度[22],稳定平台的倾斜角与扭转角应满足
| $ \begin{align} \theta \geqslant 30^{\circ} \; \;\text{ 且 }\;\; | \psi |\geqslant 20^{\circ} \end{align} $ | (13) |
即工作空间体积应满足
| $ \begin{align} V\geqslant \pi \times 30^{2}\times 40=3.6\times 10^{4}\pi (\deg^{3}) \end{align} $ | (14) |
在机构尺度参数设计空间内采用遗传算法分别求解出2个优化指标的最值,同时考虑式(15) 对工作空间体积的约束,因此有
| $ \begin{align} \begin{cases} V_{\min} =1.13\times 10^{5}\:\text{deg}^{3} \\ V_{\max} =4.52\times 10^{5}\:\text{deg}^{3} \end{cases}, \quad \begin{cases} \overline{\eta}_{\min} =0.25 \\ \overline{\eta}_{\max} =0.495 \end{cases} \end{align} $ | (15) |
综上,基于性能驱动的船载姿态稳定平台的尺寸优化问题可描述为
| $ \begin{align} \min \; \; &g(\boldsymbol{r})=1-w_{1} g_{1} (\boldsymbol{r})-w_{2} g_{2} (\boldsymbol{r}) \\ \text{s.t. }& \begin{cases} w_{1} +w_{2} =1 \\ 0<w_{1}, w_{2} <1 \\ \boldsymbol{r}\in \varOmega \end{cases} \end{align} $ | (16) |
式中,
采用改进的遗传算法对稳定平台构形优化问题进行求解。对于构形优化问题,获得全局最优值是第一要义,因普通遗传算法容易陷入局部最优解,因此本文采用小生境遗传算法,同时结合精英种群技术和自适应遗传参数调整,保证全局寻优并加快收敛速度。小生境遗传算法的优势在于保留个体多样性,避免陷入局部最优,具体手段是衡量个体相似度,并对过于相似的个体施加惩罚,降低其生存概率。
为进一步提高优化算法的性能,提出了一种新的遗传参数自适应调节律,使得交叉、变异参数依据适应度和进化代数作自适应调节,调节原则是:适应度高的个体交叉概率大,以遗传优势基因;使适应度低的个体变异概率高,以求改良基因,适应度优秀的个体也增加变异概率,以避免陷入局部最优;交叉、变异概率的限定值随进化代数作微调。具体公式如下:
| $ \begin{align} p_{{\rm c}i} & = \begin{cases} p_{{\rm cn}} +(p_{{\rm cx}} -p_{{\rm cn}}) \left(\dfrac{n}{N}+\dfrac{f_{i}} {\overline{f}}-\dfrac{nf_{i}} {N\overline{f}}\right), & f_{i} \leqslant \overline{f} \\ p_{{\rm cx}}, & f_{i} >\overline{f} \end{cases} \end{align} $ | (17) |
| $ \begin{align} p_{{\rm m}i} & = \begin{cases} p_{{\rm mn}} +(p_{{\rm mx}} -p_{{\rm mn}})\left(1-\dfrac{n}{N}\right)\dfrac{f_{i} -\overline{f}}{f_{\max} -\overline{f}}, & f_{i} \geqslant \overline{f} \\ p_{{\rm mx}} -(p_{{\rm mx}} -p_{{\rm mn}})\dfrac{n}{N}, & f_{i} <\overline{f} \end{cases} \end{align} $ | (18) |
式中,
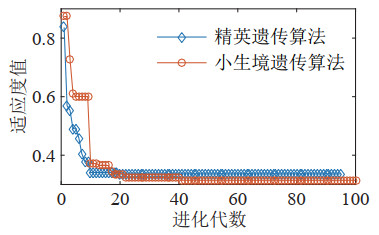
考虑计算时间成本,取种群规模为100,精英种群规模为10,采用实数编码,交叉概率最值分别取为0.6、0.9,变异概率最值分别取为0.005、0.01,小生境半径取为0.052,最大进化代数为100。经迭代计算,算法逐渐收敛到最佳结果(如图 6所示),目标函数值为0.3287。
|
图 6 遗传算法迭代图 Fig.6 Iteration of the genetic algorithm |
另采用精英遗传算法[24]求解此问题,与之相比,本文所用小生境遗传算法从原理上兼顾了保留最优基因和保持种群多样性,因此可以更好地逼近全局最优解,求解精度更高。优化所得船载稳定平台的最佳综合性能指标为0.6713,该性能指标所对应的最佳几何尺度参数为
对优化算法得到的最优构形与前述实例中采用的构形进行性能对比,检验优化方法是否有效。
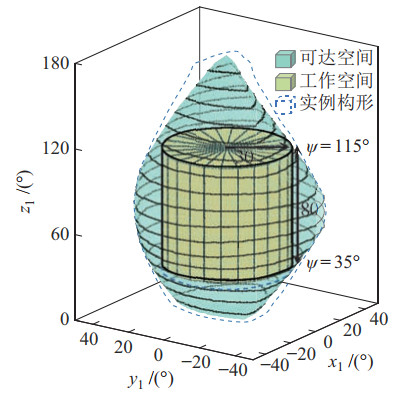
图 7为优化所得最佳构形的工作空间。相对于实例构形(图中虚线轮廓所示),最佳构形的可达空间略有收缩。在倾斜角
|
图 7 最佳构形的工作空间 Fig.7 Workspace of the optimal configuration |
图 8为最佳构形与实例构形的力传递性能对比情况。由前述分析可知,初始构形的局部力传递率最高不到0.4,全域力传递率为0.34。与之相比,优化后的最佳构形的局部力传递率最高可达0.495,全域力传递率达到0.46,力传递性能提升明显。综合来看,优化所得最优构形在工作空间体积方面虽稍有减小,但机构的力传递性能有了显著的提高,综合性能更好。意味着优化所得的船载稳定平台基本保持了原有的舰船姿态角补偿范围,并且在同等驱动能力下可大幅度提高稳定平台的载荷能力与动态姿态角补偿能力。

|
图 8 力传递率对比 Fig.8 Comparison of the force transmission rate |
以上述优化结果为基础,设计并制造了船载稳定平台的实验样机,如图 9所示。

|
图 9 实验样机 Fig.9 Experimental prototype |
其关键尺度参数分别为:静平面半径
为验证机构工作空间,控制动平台在工作空间内运动,重点验证其能否到达所设计工作空间的边界点位,例如:指定某扭转角
样机的实验结果如图 10所示,图中红色曲线为在理论工作空间中挑选的各层边界,蓝色圆圈为实验样机的实际运动点位。图中,样机的扭转角运动范围达到

|
图 10 工作空间点位验证 Fig.10 Verification of the workspace point |
图 11展示了样机的几种极限位形。观察到影响样机工作空间大小的约束因素有电缸行程、关节转角极限值等。其中关节转角极限是限制机构工作空间的主要因素,而电缸行程严格意义上并不属于约束因素,因为它是根据平台在工作空间运动所需的杆长范围而选定的。奇异位形也不会影响到样机运动,因为求解工作空间时已经避开了位形奇异点。

|
图 11 样机极限位形 Fig.11 Prototype's extreme pose |
稳定平台设计额定载荷为20 kg,由3台50 W伺服电机驱动,电机额定扭矩0.15 N

|
图 12 带负载的稳定平台 Fig.12 Stable platform with load |
|
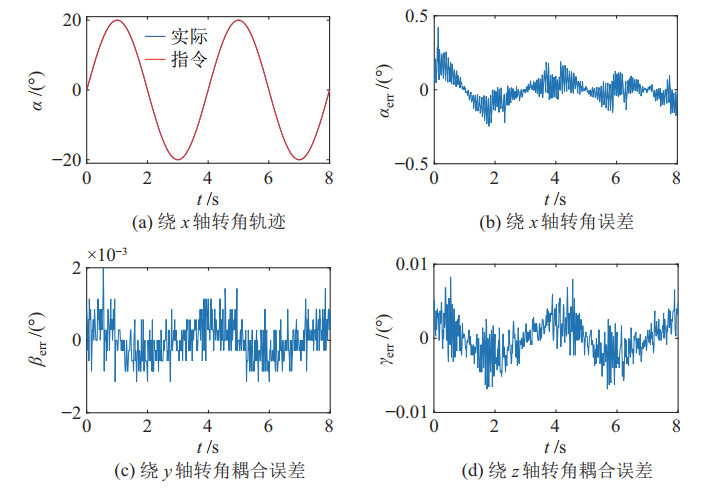
图 13 轨迹跟踪曲线与误差 Fig.13 Curve and error of trajectory tracking |
同时测量了绕
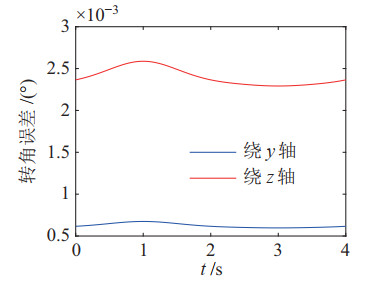
|
图 14 转角误差对比 Fig.14 Comparison of the angle error |
上文针对权重相等的情况开展了构形优化,为进一步揭示权重赋值对优化结果的影响,本节逐渐改变权值,并分别开展构形优化工作。
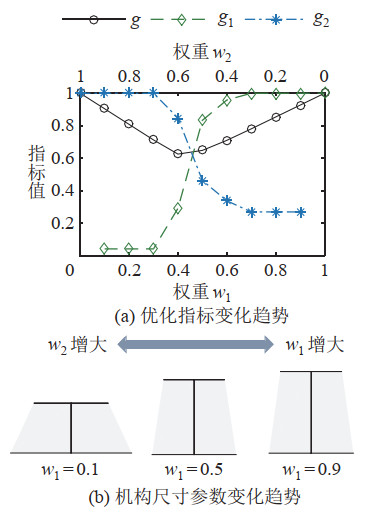
当权重
|
图 15 不同权重下的结果对比 Fig.15 Comparison of results under different weights |
图 15(b)展示了最佳构形比例随权重取值的变化情况,为使构形间具有可比性,各构形均已作归一化处理。随着工作空间权重
针对船载稳定平台的尺度参数优化问题,以3-UPS & S并联机构为对象,考虑各类约束,利用数值搜索法完成了工作空间的求解;基于力雅可比矩阵逆矩阵的最小奇异值定义力传递率;以工作空间体积和全域力传递率的加权和为综合优化目标,采用小生境自适应遗传算法优化得到了稳定平台的最佳尺度参数。与初始构形相比,最佳构形在全域力传递率方面提升了35%,综合运动学性能得到增强。制作样机并完成相关实验,结果表明样机实际运动能力与理论优化性能匹配,验证了所做优化设计的有效性。最后探究了指标权重取值对最优构形的影响,工作空间权重增大使得最佳构形更窄更高;力传递率权重增加使得机构更宽更矮;权重取值均衡时,最佳构形各方面性能适中,综合性能占优。
研究过程中重点结合了实际场景中的应用需求,设定了设计流程中的各类约束,并且在优化算法中提出了遗传参数自适应调整律,以求获得全局最优解并提高计算效率。为进一步提高该船载稳定平台的运动性能,未来应当改进其运动控制算法,提高稳定精度和鲁棒性。
| [1] |
刘晓, 赵铁石, 边辉, 等. 耦合型3自由度并联稳定平台机构动力学分析[J]. 机械工程学报, 2013, 49(1): 45-52. Liu X, Zhao T S, Bian H, et al. Dynamics analysis of a 3-DOF coupling parallel mechanism for stabilized platform[J]. Journal of Mechanical Engineering, 2013, 49(1): 45-52. |
| [2] |
黄真, 赵永生, 赵铁石. 高等空间机构学[M]. 北京: 高等教育出版社, 2006. Huang Z, Zhao Y S, Zhao T S. Advanced spatial mechanism[M]. Beijing: Higher Education Press, 2006. |
| [3] |
Gosselin C M, Jean M. Determination of the workspace of planar parallel manipulators with joint limits[J]. Robotics and Autonomous Systems, 1996, 17(3): 129-138. DOI:10.1016/0921-8890(95)00039-9 |
| [4] |
Aboulissane B, El Haiek D, El Bakkali L, et al. On the workspace optimization of parallel robots based on CAD approach[J]. Procedia Manufacturing, 2019, 32: 1085-1092. DOI:10.1016/j.promfg.2019.03.065 |
| [5] |
Castelli G, Ottaviano E, Ceccarelli M. A fairly general algorithm to evaluate workspace characteristics of serial and parallel manipulators[J]. Mechanics Based Design of Structures and Machines, 2008, 36(1): 14-33. DOI:10.1080/15397730701729478 |
| [6] |
Peidró A, Reinoso Ó, Gil A, et al. An improved Monte Carlo method based on Gaussian growth to calculate the workspace of robots[J]. Engineering Applications of Artificial Intelligence, 2017, 64: 197-207. DOI:10.1016/j.engappai.2017.06.009 |
| [7] |
Bohigas O, Manubens M, Ros L. A complete method for workspace boundary determination on general structure manipulators[J]. IEEE Transactions on Robotics, 2012, 28(5): 993-1006. DOI:10.1109/TRO.2012.2196311 |
| [8] |
Rouhani E, Nategh M J. Workspace, dexterity and dimensional optimization of microhexapod[J]. Assembly Automation, 2015, 35(4): 341-347. DOI:10.1108/AA-03-2015-020 |
| [9] |
张新. 一种3-UPS/S球面并联机构的运动参数优化研究[D]. 秦皇岛: 燕山大学, 2013. Zhang X. Optimization of motion parameters of a 3-UPS/S spherical parallel mechanism[D]. Qinhuangdao: Yanshan University, 2013. |
| [10] |
Chen X, Chen C, Liu X J. Evaluation of force/torque transmission quality for parallel manipulators[J]. Journal of Mechanisms and Robotics, 2015, 7(4). DOI:10.1115/1.4029188 |
| [11] |
Liu X J, Wu C, Wang J S. A new approach for singularity analysis and closeness measurement to singularities of parallel manipulators[J]. Journal of Mechanisms and Robotics, 2012, 4(4). DOI:10.1115/1.4007004 |
| [12] |
Wu G L, Zou P. Comparison of 3-DOF asymmetrical spherical parallel manipulators with respect to motion/force transmission and stiffness[J]. Mechanism and Machine Theory, 2016, 105: 369-387. DOI:10.1016/j.mechmachtheory.2016.07.017 |
| [13] |
Liu H T, Huang T, Kecskeméthy A, et al. A generalized approach for computing the transmission index of parallel mechanisms[J]. Mechanism and Machine Theory, 2014, 74: 245-256. DOI:10.1016/j.mechmachtheory.2013.12.012 |
| [14] |
刘海涛, 熊坤, 贾昕胤, 等. 3自由度冗余驱动下肢康复并联机构的运动学优化设计[J]. 天津大学学报(自然科学与工程技术版), 2018, 51(4): 357-366. Liu H T, Xiong K, Jia X Y, et al. Kinematic optimization of a redundantly actuated 3-DOF parallel mechanism for lower-limb rehabilitation[J]. Journal of Tianjin University (Natural Science and Engineering Technology Edition), 2018, 51(4): 357-366. |
| [15] |
叶伟, 谢镇涛, 李秦川. 一种可用于微创手术的并联机构运动学分析与性能优化[J]. 机械工程学报, 2020, 56(19): 103-112. Ye W, Xie Z T, Li Q C. Kinematics analysis and performance optimization of a parallel manipulator for minimally invasive surgery[J]. Journal of Mechanical Engineering, 2020, 56(19): 103-112. |
| [16] |
陈为林, 冯梓泓, 卢清华, 等. 多模式刚柔结合欠驱动抓取机构的设计、分析与实验测试[J]. 机器人, 2022, 44(2): 139-152. Chen W L, Feng Z H, Lu Q H, et al. Design, analysis and experimental test of a multi-mode rigid-flexible underactuated grasping mechanism[J]. Robot, 2022, 44(2): 139-152. |
| [17] |
肖宇光, 高峰. 基于多约束条件下的机器人尺寸综合优化[J]. 机械设计, 2021, 38(4): 1-8. Xiao Y G, Gao F. Dimension optimization of robots based on multi-constraints[J]. Machine Design, 2021, 38(4): 1-8. |
| [18] |
温海营, 戴敏, 张慧, 等. 含被动高副的冗余驱动并联机器人优化设计[J]. 机器人, 2021, 43(6): 694-705. Wen H Y, Dai M, Zhang H, et al. Optimal design of a redundantly actuated parallel robot with passive higher kinematic pair[J]. Robot, 2021, 43(6): 694-705. |
| [19] |
程元皓, 王孙安, 于德弘. 仿生并联眼动机构多目标优化设计[J]. 机器人, 2017, 39(2): 176-181. Cheng Y H, Wang S A, Yu D H. Multi-objective optimization design of a bionic parallel oculogyric mechanism[J]. Robot, 2017, 39(2): 176-181. |
| [20] |
Shen Y, Jia Q X, Chen G, et al. Study of rapid collision detection algorithm for manipulator[C]//IEEE 10th Conference on Industrial Electronics and Applications. Piscataway, USA: IEEE, 2015: 934-938.
|
| [21] |
Li B K, Wang K, Han Y G, et al. Singularity property and singularity-free path planning of the Gough-Stewart parallel mechanism[J]. International Journal of Advanced Robotic Systems, 2017, 14(6). DOI:10.1177/1729881417734971 |
| [22] |
杨建涛. 并联折叠式舰载稳定平台机构分析与控制理论研究[D]. 秦皇岛: 燕山大学, 2015. Yang J T. Mechanism analysis and control theory research on ship-based stabilizing platform with foldable parallel mechanism[D]. Qinhuangdao: Yanshan University, 2015. |
| [23] |
郭菲. 电液驱动3-UPS/S并联稳定平台机构优化及动力学模型研究[D]. 秦皇岛: 燕山大学, 2016. Guo F. Research on dynamic model and optimization of electro-hydraulic 3-UPS/S parallel stabilized platform[D]. Qinhuangdao: Yanshan University, 2016. |
| [24] |
Zhang H Z, Liu F, Zhou Y Y, et al. A hybrid method integrating an elite genetic algorithm with tabu search for the quadratic assignment problem[J]. Information Sciences, 2020, 539: 347-374. |
 2023, Vol. 45
2023, Vol. 45


