1 引言（Introduction）

目前，四足机器人正由学术研究走向商业应用。虽然实用性的曙光已经出现，但是走向技术成熟、普及应用还面临诸多难题，其中最具有挑战性的是功能丰富、运算简洁、成本低廉的控制器设计。四足机器人由于关节自由度多、运动规划问题复杂，与动物相比其运动模式欠缺。另外，真实地形波动将导致在行走过程中出现不可预测的足地碰撞，会造成姿态不稳定问题。这些问题使四足机器人的运动控制任务变得复杂。为了解决四足机器人复杂的运动控制，国内外学者提出了各种控制方法，从简化模型到完整动力学模型、从瞬时控制到预测控制、从轨迹优化到智能学习。其中最具代表性的控制方法有：1) 基于简化模型的弹簧负载倒立摆（SLIP）模型控制、虚拟模型控制（VMC）；2) 基于完整动力学模型的零力矩点（ZMP）稳定性判据控制、模型预测控制（MPC）、全身控制（WBC）；3) 基于生物神经和脑控制机理的CPG控制、强化学习和深度强化学习控制。

SLIP模型^[1]将腿部简化为一个带负载的无质量弹簧，通过三分量方法实现机器人跳跃控制，因其原理简单、实用性强被许多机构和高校广泛采用，如波士顿动力公司^[1]、杭州宇树科技有限公司^[2]、山东大学^[3]等。但是SLIP模型无法直接设定步频、周期等与时间相关的参数，在实现疾驰（gallop）等非对称步态和步态转换方面存在不足。VMC方法^[4]适合处理机器人与地形的动态交互，其原理是：在机器人质心处施加虚拟力和虚拟力矩，根据一定的规则将虚拟力和虚拟力矩分配给支撑腿，并转化为足端力，再通过腿机构的雅可比矩阵转化为关节力矩，从而控制机器人到达期望的位姿。VMC方法不需要精确的动力学模型，能以相对较小的计算量实现显著的控制效果。但是在某些特殊机器人构形下会出现腿机构雅可比矩阵不满秩的情况，需要舍弃相关的受控自由度^[5-6]。

ZMP控制假设在机器人的支撑多边形内有一点，使得机器人受到的地面反作用力与重力、惯性力平衡，根据这个稳定性判据规划机器人的运动轨迹，对控制低速运动具有较好效果^[7-8]。但是，ZMP方法存在以下不足：需要准确的动力学模型以及环境模型、无法对扰动作出快速响应、轨迹规划过程比较耗时、不适用于有柔性环节的被控对象。WBC方法^[9-10]的核心思想是：针对完整的机器人动力学模型，构建一个带优先级的多任务控制组织架构，将所有可控自由度的控制任务按照重要程度分成不同的优先级，运动过程中先满足高优先级的任务要求。Bellicoso等^[11]利用WBC方法来优化四足机器人ANYmal的全身运动和接触力，实现了行走（walk）、对角（trot）、溜步（pace）步态的运动和后2种步态的互相转换。由于WBC方法采用带浮动基的完整动力学模型，对控制硬件要求很高，在控制跳跃等具有飞行相的运动时效果不理想^[12]。Kim等^[13]结合MPC^[14-17]和WBC方法设计了MIT Cheetah系列四足机器人控制器，通过MPC方法对多个控制周期的运动进行预测，求得较长时间内的最优地面反作用力，WBC方法根据求得的地面反作用力，应用完整动力学模型求得关节力矩、位置和速度。MPC方法的局限在于需要在线解算复杂的优化算法，计算量大，难以获得较高的控制带宽。

四足机器人运动控制的另一技术路线是无模型控制。其中CPG控制方法^[18]源于动物节律运动神经控制机理，由多个振荡器单元组成分布式网络，各振荡器输出之间具有强耦合，通过改变振荡器之间的连接权重得到不同相位关系。CPG控制避免了繁琐的动力学模型，计算量小、鲁棒性强，在多自由度协调和步态转换等控制任务方面具有明显优势^[19-21]。但是，CPG网络的强耦合性降低了机器人运动的灵活性，不利于适应复杂地形。随着人工智能的发展，以强化学习和深度强化学习为代表的智能学习控制逐渐成为四足机器人运动控制领域的研究热点。基于大数据驱动的智能学习控制无需对环境精确建模，机器人在与环境互动过程中不断完善自身知识库，主动适应新的环境^[22-24]。智能学习控制类似于人脑的随意运动控制，需要大量的训练，且会遇到虚实迁移的瓶颈问题，目前还不成熟。

仿猎豹机器人模仿猎豹的躯体结构和运动模式，以实现高速运动为目标，一般是在四足机器人中加入柔性脊柱或躯干关节来实现。脊柱关节增加了仿猎豹机器人的机构自由度数和运动复杂性，对高速运动控制提出了更大挑战。波士顿动力公司的仿猎豹四足机器人Cheetah具有1个铰接式脊柱关节，在跑步机上实现了12.6 m/s的奔跑速度^[25]，具有胸腰2个脊柱关节的WildCat以8.5 m/s的速度刷新了四足机器人户外奔跑的最快速度记录^[26]。麻省理工学院的Kim^[27]将被动柔性脊柱与后腿运动差分耦合，使仿猎豹机器人Cheetah I的奔跑速度达到6 m/s。哈尔滨工业大学的蔡昌荣^[28]针对具有双关节脊柱的平面型四足机器人，提出基于SLIP迁移模型的脊—腿协调控制策略，实现了2.5 m/s的跳跃（bound）步态奔跑。上海交通大学的王石刚团队^[29]基于动量理论，实现了具有双关节脊柱的四足机器人SQBot II的疾驰（gallop）步态运动。哈尔滨工程大学的陈东良团队^[30-31]对脊柱关节数目、刚度以及步态参数对运动性能和能量利用效率的影响进行了理论研究。

自然界总是为工程设计提供灵感。动物的运动行为从神经控制机理角度可以分为周期性模式运动、由外界刺激引起的反射运动、受主观意识支配的随意运动。模式运动的中心控制单元是位于脊髓中的中枢模式发生器（CPG），控制走、跑等节律性的步态。当地形变化时会有反射运动参与，通过底层反射弧整合躯体感觉信号和运动信号，调节CPG输出。当环境或行为非常复杂时，大脑高层中枢将参与运动调节，利用随意运动达成运动目标^[18]。动物的3种运动模式相互配合，使动物具备丰富的运动模式，能够适应多变的外界环境。动物不同运动模式具有不同的神经控制区，应用不同的控制机理，这种模块化分层融合的神经控制结构对于四足机器人控制器设计具有深刻的启发意义。

本文研究的仿猎豹四足机器人具有2DOF脊柱关节和3DOF腿机构，整机包含14个自由度，具备3维空间复杂运动能力。为了实现仿猎豹四足机器人在复杂地形下的高速运动控制，本文模仿动物神经系统中多模型融合的控制机理，提出一种四足机器人多模型分层控制架构：第1层为基于SLIP模型的单腿控制，第2层为基于CPG网络的脊柱与腿、腿与腿之间的自由度协调控制，第3层为基于VMC的机器人—环境交互控制，各层之间通过基于CPG节律性状态的有限状态机进行融合。最后在仿真软件Webots中通过崎岖地形和步态转换实验验证方法的有效性。

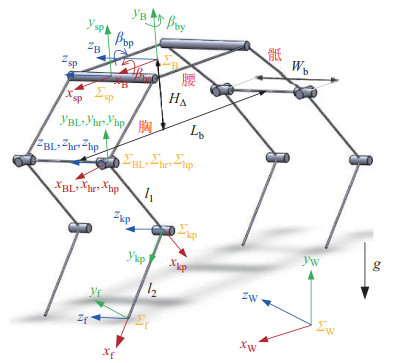
2 具有脊柱关节的仿猎豹四足机器人（Cheetah-mimicking quadruped robot with spine joints） 2.1 样机

仿猎豹四足机器人有1条脊柱和4条腿，共14个自由度。脊柱由胸、腰、骶串联构成，有2个主动俯仰自由度，通过改变胸部和骶部相对于腰部的姿态来模拟猎豹脊柱的屈伸运动。腿部结构分为大腿、小腿和足，足与小腿固连，每条腿包含1个横滚髋关节、1个俯仰髋关节和1个俯仰膝关节。四足机器人机构模型见图 1，整机重150 kgf，尺寸为1.5 m$ \times $0.665 m$ \times $1.18 m，其他参数见表 1。

2.2 运动学模型

仿猎豹四足机器人坐标系如图 1所示。$ \varSigma_{\rm W} $为世界坐标系；$ \varSigma_{\rm B} $为机体基坐标系，附在腰部的几何中心并随腰部运动，作为机器人整体参考坐标系，$ x_{\rm B} $轴指向机器人前进方向；$ \varSigma_{\rm sp} $为脊柱关节坐标系；$ \varSigma_{\rm BL} $为腿部基坐标系，其方向始终保持与$ \varSigma_{\rm B} $系相同。$ \varSigma_{\rm hr} $为髋关节横滚坐标系；$ \varSigma_{\rm hp} $为髋关节俯仰坐标系；$ \varSigma_{\rm kp} $为膝关节俯仰坐标系；$ \varSigma_{\rm f} $为足端坐标系。由正运动学求得足端在$ \varSigma_{\rm B} $系中的坐标$ ( x_{\rm f}^{\rm B}, y_{\rm f}^{\rm B}, z_{\rm f}^{\rm B}) $：

$ \begin{align} \begin{cases} x_{\rm f}^{\rm B} =l_{1} \cos \theta_{2}+l_{2} \cos (\theta_{2} +\theta_{3})+\dfrac{\delta L_{\rm b}} {2} \\ y_{\rm f}^{\rm B} =[l_{1} \sin \theta_{2}+l_{2} \sin (\theta_{2} +\theta_{3})]\cos \theta_{1}-H_{\Delta} \\ z_{\rm f}^{\rm B} =-[l_{1} \sin \theta_{2}+l_{2} \sin (\theta_{2} +\theta_{3})]\sin \theta_{1}+\dfrac{\lambda W_{\rm b}} {2} \end{cases}\end{align} $

(1)

式中，$ \lambda $、$ \delta $为符号变量，前腿$ \lambda =1 $，后腿$ \lambda =-1 $，左腿$ \delta =1 $，右腿$ \delta =-1 $。

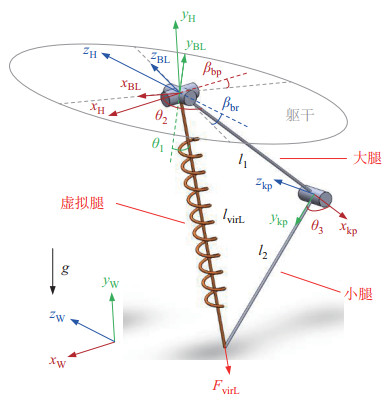
如图 2所示，连接髋关节中心和足端，构造虚拟腿，根据几何关系求得虚拟腿长$ l_\text{virL} $为

$ \begin{align} l_\text{virL} =\sqrt{l_{1}^{2} +l_{2}^{2} -2l_{1} l_{2} \cos ({\pi} -\theta_{3})} \end{align} $

(2)

腿部运动学逆解为

$ \begin{align} \begin{cases} \theta_{1} =\arctan \dfrac{z_{\rm f}^{\rm BL}} {y_{\rm f}^{\rm BL}} \\[10pt] \theta_{2} =-\dfrac{\pi} {2}- \left(\arctan \dfrac{x_{\rm f}^{\rm BL}} {y_{\rm f}^{\rm BL}} +\arcsin \dfrac{l_{2} \sin ({\pi} -\theta_{3})}{l_\text{virL}}\right) \\[10pt] \theta_{3} ={\pi} -\arccos \dfrac{l_\text{virL}^{2} -l_{1}^{2} -l_{2}^{2}} {-2l_{1} l_{2}} \end{cases} \end{align} $

(3)

对式(1)(3) 求偏微分得到足端相对于$ \varSigma_{\rm B} $坐标系的雅可比矩阵为

$ \begin{align} {{\mathit{\boldsymbol{J}}}}= \begin{bmatrix} 0 & {-l_{1} { s}_{2} -l_{2} { s}_{23}} & {-l_{2} { s}_{23}} \\ {-l_{1} { s}_{1} { s}_{2} -l_{2} { s}_{1} { s}_{23}} & {l_{1} { c}_{1} { c}_{2} +l_{2} { c}_{1} { c}_{23}} & {l_{2} { c}_{1} { c}_{23}} \\ {-l_{1} { c}_{1} { s}_{2} -l_{2} { c}_{1} { s}_{23}} & {-l_{1} { s}_{1} { c}_{2} -l_{2} { s}_{1} { c}_{23}} & {-l_{2} { s}_{1} { c}_{23}} \end{bmatrix} \end{align} $

(4)

式中，$ { s}_{i} =\sin \theta_{i} $，$ { c}_{i} =\cos \theta_{i} $，$ { s}_{ij} =\sin (\theta_{i} +\theta_{j}) $，$ { c}_{ij} =\cos (\theta_{i} +\theta_{j}) $，$ i, j=1, 2, 3 $，$ i\ne j $。

3 四足机器人多模型分层控制方法（Multi-model hierarchical control method for the quadruped robot）

具有脊柱关节的仿猎豹四足机器人的自由度较多，完整动力学的建模过程非常复杂，而且难以得到精确模型，难以实施有效的控制。因此，提出一种多模型分层控制架构，如图 3所示，各层控制方法之间解耦，自下而上将控制系统分为3个层次：底层为单腿控制层，采用SLIP模型，对膝关节自由度实施控制，实现躯体平衡与速度控制；第2层为协调层，采用CPG模型，对髋关节俯仰自由度实施控制，实现脊—腿协调、步态生成与转换；最高层为适应层，采用VMC模型，对髋关节横滚自由度实施控制，实现机器人偏航姿态控制。各层之间通过基于CPG输出的有限状态机（C-FSM）进行融合。

3.1 基于SLIP模型的单腿跳跃控制

将四足机器人的每条腿等效为带负载的无质量弹簧，该虚拟弹簧连接腿部的髋关节和足端，称为虚拟腿，通过控制膝关节俯仰角可使虚拟腿模拟弹簧运动。如图 2所示，$ F_\text{virL} $为作用在足端的虚拟弹簧力。采用Raibert提出的三分控制法^[1]将跳跃过程解耦为跳跃高度控制、水平速度控制和姿态控制。在支撑相，腿部通过地面反作用力控制跳跃高度和姿态。在腾空相，通过控制落足点的位置来改变下一次跳跃的水平速度。

3.1.1 跳跃高度控制

在支撑相，通过调整腿部虚拟弹簧力来改变足端受到的地面反作用力，从而实现跳跃高度控制。虚拟弹簧力$ F_\text{virL} $为

$ \begin{align} F_\text{virL} =k_{\text{ps}} (l_\text{virL} -l_\text{virL0})+k_{\text{vs}} \dot{l}_\text{virL} \end{align} $

(5)

式中，$ k_{\text{ps}} $为虚拟弹簧位置增益，$ k_{\text{vs}} $为虚拟弹簧速度增益，$ l_\text{virL0} $为虚拟弹簧原长。

为了弥补阻尼造成的能量损失，在虚拟腿支撑相的伸展阶段为腿部补充额外的推力，补充推力$ F_{\text{add}} $的大小依据仿生学机理来设定。根据Hudson等^[32]的研究，猎豹和灰狗在奔跑时足端力随速度的增大而增大，通过改变支撑相的垂直冲量来调整跳跃高度。采用对数曲线近似拟合文[32] 给出的猎豹足端峰值力与速度之间的关系：

$ \begin{align} \gamma =\log_{a} (\dot{x}+1) \end{align} $

(6)

式中，$ \dot{x} $为猎豹奔跑速度，$ a=2.779 $为拟合确定的对数底数。

在虚拟腿支撑相的伸展阶段将虚拟弹簧力调整为

$ \begin{align} F_{\text{virL_T}} =F_\text{virL} +\gamma F_{\text{add}} \end{align} $

(7)

式(7) 将支撑相的虚拟弹簧力与期望速度关联，实现虚拟弹簧力的动态变化，从而实现不同速度下跳跃高度的控制。

在腾空相，采用比例—微分（PD）控制器控制虚拟腿缩短至指定长度来避障，所需施加的虚拟弹簧力为

$ \begin{align} F_{\text{virL_S}} =k_{\text{ps}} (l_\text{virL} -l_\text{virL}^{\rm d})+k_{\text{vs}} \dot{l}_\text{virL} \end{align} $

(8)

式中，$ l_\text{virL}^{\rm d} $为虚拟腿期望长度。

根据式(5)(7)(8) 确定各阶段的虚拟弹簧力之后，将其看作足端的输出力，利用雅可比矩阵将足端输出力映射成所需的等效关节力矩：

$ \begin{align} {\mathit{\boldsymbol{\tau}}}^{\rm h}=\mathit{\boldsymbol{J}}^{\rm T}{\mathit{\boldsymbol{F}}}_\text{virL} \end{align} $

(9)

式中，$ {\mathit{\boldsymbol{\tau}}}^{\rm h}=[\tau_{\text{hr}}^{\rm h}, \tau_{\text{hp}}^{\rm h}, \tau_{\rm kp}^{\rm h}]^{\rm T} $，各分量分别代表横滚髋关节、俯仰髋关节、俯仰膝关节的等效力矩，$ {\mathit{\boldsymbol{F}}}_\text{virL} =[F_\text{virLx}, $ $ F_\text{virLy}, $ $ F_\text{virLz}]^{\rm T} $为虚拟弹簧力。

3.1.2 水平速度控制

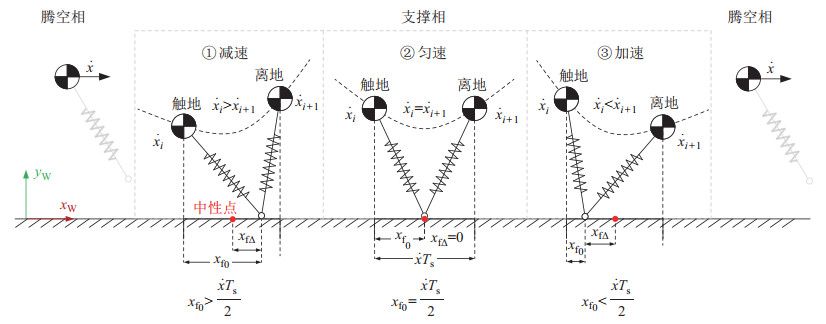
SLIP模型在腾空相时为斜抛运动，在足端触地前规划好落足点的位置，足端触地后水平速度发生改变，从而控制下一个运动周期的水平速度。如图 4所示，$ x_{\rm f_{0}} $为足端相对于SLIP模型质心的前向位移，$ \dot{x} $为质心的前向水平速度，$ T_{\rm s} $为支撑相时间。当$ x_{\rm f_{0}} ={\dot{x}T_{\rm s}} /2 $时，足端处于SLIP模型运动的中性点位置。定义$ \Delta \dot{x}=\dot{x}_{i+1} -\dot{x}_{i} $为SLIP模型一个周期内的速度增量，其大小由落足点的位置决定。若落足点位于中性点右侧，在支撑相有部分动能转化为重力势能，速度增量小于0；若落足点位于中性点，离地时与触地时的动势能相同，速度增量为0；若落足点位于中性点左侧，在支撑相有部分重力势能转化为动能，速度增量大于0。

根据图 4的速度调节原理，在落足点位于中性点的基础上再附加一个偏移量$ x_{{\rm f}\Delta} $，实现SLIP模型的加减速运动，采用水平速度的线性估计来确定该偏移量：

$ \begin{align} x_{{\rm f}\Delta} =k_{\dot{x}} (\dot{x}-\dot{x}_{\rm d}) \end{align} $

(10)

式中，$ \dot{x}_{\rm d} $为期望水平速度，$ k_{\dot{x}} $为速度增量系数，决定了实际速度到达期望速度的快慢。

综上所述，在某一期望水平速度下期望落足点的位置为

$ \begin{align} x_{\rm f} =\frac{\dot{x}T_{\rm s}} {2}+k_{\dot{x}} (\dot{x}-\dot{x}_{ \rm d}) \end{align} $

(11)

根据式(3) 逆运动学求得期望的俯仰髋关节角$ \theta_{\text{hp}}^{\rm d} $，采用力矩控制使足端运动至期望的落足点：

$ \begin{align} \tau_{\text{hp}}^{\rm v} =-k_{{\text{php}}} (\theta_{2} -\theta_{2}^{\rm d})-k_{{\text{vhp}}} \dot{\theta}_{2} \end{align} $

(12)

式中，$ k_{{\text{php}}} $为俯仰髋关节位置增益，$ k_{{\text{vhp}}} $为俯仰髋关节速度增益。

3.1.3 姿态控制

在腾空相时调整身体姿态较为困难，而在触地相时足端与地面的摩擦力允许髋关节对机体施加较大的扭矩去改变机身姿态，所以在支撑相通过控制髋关节扭矩来调整身体姿态。以力矩控制身体姿态，期望的俯仰、横滚髋关节角都为0，所以髋关节力矩为

$ \begin{align} \tau_{\text{hp}}^{\rm o} & =-k_{{\text{php}}} \beta_{\text{bp}} -k_{{\text{vhp}}} \dot{\beta}_{\text{bp}} \end{align} $

(13)

$ \begin{align} \tau_{\text{hr}}^{\rm o} & =-k_{{\text{phr}}} \beta_{\text{br}} -k_{{\text{vhr}}} \dot{\beta}_{\text{br}} \end{align} $

(14)

式中，$ k_{{\text{phr}}} $为横滚髋关节位置增益，$ k_{{\text{vhr}}} $为横滚髋关节速度增益。

3.1.4 腿部重力补偿

SLIP模型将机体质量全部集中到髋部质心而忽略腿部质量，因此腿部运动不会影响机器人整体的运动。对于两段式腿机构而言，腿部重力对触地点或机身质心始终有力矩作用，且力臂较长，若忽略腿部质量会造成机身向重力侧倾倒。因此需要进行重力补偿。设腿部为均质杆，质心位于杆的几何中心，则腿部对各关节的重力矩为

$ \begin{equation} \begin{aligned} M_{\text{hr}} =\, & \frac{1}{2}m_{1} gl_{1} \sin \theta_{\text{hr}}+ \\ & m_{2} g\big({l_{2} \cos \theta_{2} +\frac{1}{2}l_{2} \cos (\theta_{2} +\theta_{3})} \big)\sin \theta_{\text{hr}} \\ M_{\text{hp}} =\, & -\frac{1}{2}m_{1} gl_{1} \cos \theta_{2}- \\ & m_{2} g\big({l_{2} \cos \theta_{2} +\frac{1}{2}l_{2} \cos (\theta_{2} +\theta_{3})} \big) \\ M_{\rm kp} =\, & -\frac{1}{2}m_{2} gl_{2} \sin (-\theta_{2} -\theta_{3})\cos \theta_{3} \end{aligned} \end{equation} $

(15)

各关节所需补偿的力矩为

$ \begin{align} \tau_{i}^{\rm g} =-M_{i}, \; \; \; i={\rm hr, hp, kp} \end{align} $

(16)

综合式(9)(12)(13)(14)(16)，单腿控制中各关节的最终合力矩为

$ \begin{align} \begin{cases} \tau_{\text{hp}} =\tau_{\text{hp}}^{\rm h} +\tau_{\text{hp}}^{\rm v} +\tau_{\text{hp}}^{\rm o} +\tau_{\text{hp}}^{\rm g} \\ \tau_{\text{hr}} =\tau_{\text{hr}}^{\rm h} +\tau_{\text{hr}}^{\rm o} +\tau_{\text{hr}}^{\rm g} \\ \tau_{\rm kp} =\tau_{\rm kp}^{\rm h} +\tau_{\rm kp}^{\rm g} \end{cases} \end{align} $

(17)

3.2 基于CPG的脊柱—腿协调控制 3.2.1 CPG模型

仿猎豹四足机器人的脊柱具有2个主动关节，为了协调腿关节与脊柱关节的运动，生成对角、疾驰等多种步态，采用基于生物神经控制机理的CPG模型进行控制。以左前腿为基准振荡器，将4条腿的俯仰髋关节以及脊柱关节进行耦合，建立如图 5所示的四足机器人CPG网络拓扑图，其中1 ~4分别表示左前腿（FL）、右前腿（FR）、左后腿（HL）和右后腿（HR）俯仰髋关节，5表示胸部关节，6表示骶部关节，$ \varphi_{ij} $（$ i, j=1, 2, \cdots, 6 $，$ i\ne j $）为各关节之间的相位差，双向箭头表示两者之间有相位调节因子，单向箭头表示单相耦合，直线连接表示两者有固定相位差。

采用余弦振荡器对CPG进行建模，根据图 5给出CPG的数学模型：

$ \begin{align} \begin{cases} y_{1} =A_{1} \cos (\omega t+\varphi_{0}) \\ y_{2} =A_{2} \cos (\omega t+\varphi_{0} +\varphi_{\rm LR}) \\ y_{3} =A_{3} \cos (\omega t+\varphi_{0} +\varphi_{\rm FH}) \\ y_{4} =A_{4} \cos (\omega t+\varphi_{0} +\varphi_{\rm LR} +\varphi_{\rm FH}) \\ y_{5} =A_{5} \cos (\omega t+\varphi_{0} +\varphi_{\rm LR}) \\ y_{6} =A_{6} \cos (\omega t+\varphi_{0} +\varphi_{\rm LR} +\varphi_{\rm FH}) \end{cases} \end{align} $

(18)

式中，$ y_{i} $（$ i=1, 2, \cdots, 6 $）为图 5中相对应的关节角，$ A_{i} $为关节运动幅值，$ \omega $为关节转动角频率，$ \varphi_{0} $为各关节初始相位，$ \varphi_{\rm LR} $为左右腿相位调节因子，$ \varphi_{\rm FH} $为前后腿相位调节因子。

根据Alexander^[33]提出的步态相位图，改变左右和前后相位调节因子，得到对角和疾驰步态的CPG模型输出信号，见图 6，图中红色实线表示支撑相，腿后摆时髋关节幅值由正转为负，处于支撑相，前摆时髋关节幅值由负转为正，处于腾空相。

3.2.2 髋关节俯仰幅值控制

对于猎豹等体型较大的动物，增大腿部摆动幅值是提高奔跑速度更为经济的方式，尤其是在高速奔跑时，速度的提高几乎全部依赖于腿部摆动幅值的增大^[34]。因此，本文将腿部摆动幅值与四足机器人速度关联，实现幅值随速度的动态调整。首先，根据SLIP模型水平速度控制确定的落足点位置，求得腿部俯仰髋关节的期望关节角$ \theta_{2}^{\rm d} $。加入增益系数对$ \theta_{2}^{\rm d} $进行调节，并根据期望速度进行补偿，得到CPG模型的俯仰髋关节幅值为

$ \begin{align} A_{i} =k_{\theta} {}^{i}\theta_{2}^{\rm d} +k_{\dot{x}} \dot{x}_{\rm d} +A_{0} \end{align} $

(19)

式中，$ i=1, 2, 3, 4 $，$ {}^{i}\theta_{2}^{\rm d} $为第$ i $个俯仰髋关节的期望关节角，$ k_{\theta} \in (0, 1 $) 为关节角增益系数，$ \dot{x}_{\rm d} $为机器人期望速度，$ A_{0} $为初始幅值。

3.2.3 步态转换控制

在CPG模型中，步态通过各腿之间的相位差来表达，对角步态与疾驰步态的前后腿相位差均为$ \pi $，对角步态的左、右腿相位差为$ \pi $，疾驰步态的左、右腿相位差为$ \pi /2 $。设定CPG模型的前后腿相位差$ \varphi_{\rm FH} =-\pi $，后腿相位滞后前腿。构造线性函数改变左、右腿相位差实现渐进性步态转换：

$ \begin{align} \varphi_{\rm LR} =\varphi_{\rm LR0} +\delta_{\text{gait}} \cdot 500\Delta \varphi_{\rm LR} t \end{align} $

(20)

式中，$ \varphi_{\rm LR0} ={\pi} $为左、右腿的初始相位差，$ \Delta \varphi_{\rm LR} =0.0025 $为左、右腿相位差增量，$ \delta_{\text{gait}} $为步态转换方向变量：

$ \begin{align} \delta_{\text{gait}} = \begin{cases} -1, & \rm{对角步态 \rightarrow 疾驰步态} \\ 1, & \rm{疾驰步态 \rightarrow 对角步态} \end{cases} \end{align} $

(21)

3.2.4 机身倾角反馈控制

机器人奔跑时，机身倾角波动太大将干扰腿部换相，容易导致机器人倾倒，因此在CPG模型中引入机身倾角反馈。

图 7为机器人奔跑时的躯干俯仰运动示意图，机器人沿$ x $方向前进。机器人步幅太大将造成腿部摆动到太过于靠前的位置，如图 7位置1所示。如果按此姿态触地，小腿处于摩擦锥之外，将导致机器人失稳。若改变CPG参数将腿部调整到位置2，让足端提前触地，使小腿处于摩擦锥之内，即可保持机器人稳定。由图 6可以看到，改变CPG模型输出信号的相位可以使曲线平移而不改变曲线的形状，从而让腿部提前或延迟进入支撑相，保持机器人稳定。因此将机身倾角作为反馈项引入CPG模型的相位项，使相位差随机身倾角动态调整。机身倾角反馈项为

$ \begin{align} \phi_{\rm f} =\mu k_{\text{bp}} \beta_{\text{bp}} +\sigma k_{\text{br}} \beta_{\text{br}} \end{align} $

(22)

式中，$ \mu $、$ \sigma $为符号变量，$ k_{\text{bp}} $和$ k_{\text{br}} $分别为机身俯仰角和横滚角的增益。

3.2.5 脊柱—腿协调控制

猎豹脊柱能够产生大幅度的屈伸运动，脊柱关节运动的幅值与奔跑速度及相应的步态有关：以对角等对称步态奔跑时脊柱屈伸运动很小，以疾驰等非对称步态奔跑时脊柱屈伸运动幅值很大。脊柱关节的运动与腿部关节运动具有特定的相位关系，在后腿触地时脊柱发生最大弯曲，随着腿的摆动，脊柱逐渐伸展，在后腿即将离地时脊柱达到最大伸展；前腿触地时，脊柱关节有类似运动规律。因此，按照猎豹的脊柱运动机理，在CPG模型中将脊柱关节运动幅值与腿部髋关节俯仰运动在相位上进行耦合，胸部关节与右前腿同相，腰部关节与右后腿同相，即$ \varphi_{46} =\varphi_{25} =0 $。根据左、右腿相位变化进行脊柱关节摆动幅值的线性差分控制：当左、右相位差为$ \pi $时，脊柱运动幅值为0；当左、右腿相位差为0时，脊柱运动达到最大幅值，即：

$ \begin{align} A_{i} =-\frac{A_{\max}} {\pi} \varphi_{\rm LR} +A_{\max}, \; \; \; i=5, 6 \end{align} $

(23)

式中，$ \varphi_{\rm LR} $为左、右腿相位差，$ A_{i} $为脊柱关节运动幅值，$ A_{\max} $为脊柱关节运动最大幅值。

脊柱的运动会耦合到腿关节，影响腿部的位置和姿态，将导致期望落足点出现偏差。如图 8所示，脊柱从位置1转动$ \Delta \theta $到达位置2，此时腿部也随之运动到位置2，其姿态发生改变，无法到达指定落足点。因此，需要将腿与脊柱的位置进行解耦，让腿部转过一个与脊柱运动方向相反的角度到达位置3，腿部姿态调整为与在位置1时相同的姿态。

综上，得到最终的CPG模型为

$ \begin{align} \begin{cases} y_{1} =A_{1} \cos (\omega t+\varphi_{0} -k_{\text{bp}} \beta_{\text{bp}} -k_{\text{br}} \beta_{\text{br}})-y_{5} \\ y_{2} =A_{2} \cos (\omega t+\varphi_{0} +\varphi_{\rm LR} -k_{\text{bp}} \beta_{\text{bp}} +k_{\text{br}} \beta_{\text{br}})-y_{5} \\ y_{3} =A_{3} \cos (\omega t+\varphi_{0} +\varphi_{\rm FH} +k_{\text{bp}} \beta_{\text{bp}} -k_{\text{br}} \beta_{\text{br}})-y_{6} \\ y_{4} =A_{4} \cos (\omega t+\varphi_{0} +\varphi_{\rm LR} +\varphi_{\rm FH} +k_{\text{bp}} \beta_{\text{bp}} +k_{\text{br}} \beta_{\text{br}}) -y_{6} \\ y_{5} =A_{5} \cos (\omega t+\varphi_{0} +\varphi_{\rm LR} -k_{\text{bp}} \beta_{\text{bp}} +k_{\text{br}} \beta_{\text{br}}) \\ y_{6} =A_{6} \cos (\omega t+\varphi_{0} +\varphi_{\rm LR} +\varphi_{\rm FH} +k_{\text{bp}} \beta_{\text{bp}} +k_{\text{br}} \beta_{\text{br}}) \end{cases} \end{align} $

(24)

3.3 基于VMC的地形适应性控制

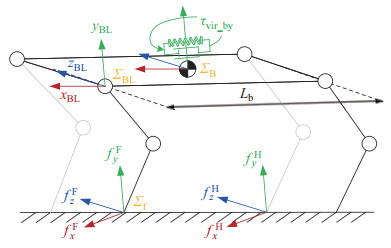
四足机器人奔跑时，地形变化将导致躯体姿态发生不受控变化，进而导致机器人失稳。本文采用VMC方法调整机身偏航姿态，提高机器人对复杂崎岖地形的适应性。机器人采用对角步态运动，如图 9所示，将作用于机身偏航方向的虚拟组件描述为安装在躯干质心的旋转弹簧阻尼器，则偏航方向的虚拟力矩为

$ \begin{align} \tau_{\rm{vir\_by}} =k_{{\text{pby}}} \beta_{\text{by}} -k_{{\text{vby}}} \dot{\beta}_{\text{by}} \end{align} $

(25)

式中，$ k_{{\text{pby}}} $为机身偏航位置增益，$ k_{{\text{vby}}} $为机身偏航速度增益。

根据力矩平衡原理，求得调整机身偏航姿态所需的横滚髋关节力矩：

$ \begin{align} \tau_{\text{hr}} =-\frac{\tau_{\text{vir_by}}} {L_{\rm b}} \cdot y_{\rm f}^{{\rm BL}} \end{align} $

(26)

式中，$ L_{\rm b} $为前后髋关节的距离，$ y_{\rm f}^{\rm BL} $为足端在$ \varSigma_{\rm BL} $坐标系中$ y $轴的坐标。

3.4 基于CPG的有限状态机

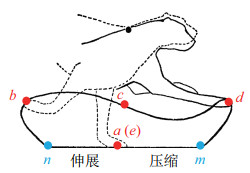
本文采用有限状态机协调各层控制模型，使其在指定时刻执行指定的控制方法。CPG作为控制核心，决定整个运动的节律，因此，采用CPG的输出作为有限状态机的触发信号。图 10为猎豹奔跑时的足端轨迹^[35]，$ m $为触地点，$ n $为离地点。将四足机器人腿部运动与猎豹腿部运动进行映射。$ an $段为施加推力段，腿部模拟弹簧施加推力；$ nb $段为收缩段，腿部缩短至一定长度，避免在前摆过程中与地面发生碰撞；$ bcd $段为腾空段，腿部保持收缩并向前摆动；$ dm $段为伸展段，腿部伸长直至接触地面；$ me $段为压缩段，腿部模拟弹簧进行压缩。为了与单腿SLIP模型运动轨迹对应，将$ dm $段与$ me $段合并为$ de $段，将$ an $段与$ nb $段合并为$ ab $段，支撑相腿部模拟弹簧施加推力，将腿部收缩放在腾空段执行。图 11为CPG模型输出的位置和速度信号曲线，$ a $至$ e $点与图 10猎豹足端轨迹中的$ a $至$ e $点一一对应。在$ bcd $段，关节速度均大于0；在$ de $段，关节速度均小于0，且关节位置大于0；在$ ab $段，关节速度均小于0，且关节位置小于0。将CPG模型输出的位置和速度状态值作为C-FSM状态切换的信号，状态切换原理如图 12所示。

3.5 四足机器人控制器设计

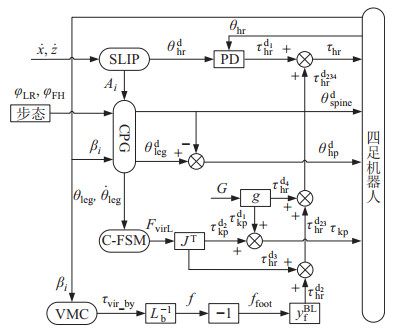
根据提出的多模型分层控制方法，设计仿猎豹四足机器人控制器，如图 13所示。控制器分为SLIP、CPG、VMC和C-FSM四个模块。SLIP模块负责单腿的运动控制，CPG模块负责协调脊柱与腿、腿与腿之间的自由度协调控制，VMC模块负责机身的偏航姿态控制，C-FSM模块负责协调腿部动作的执行。四足机器人的状态量通过反馈引入各模块，形成控制的闭环。

4 动力学仿真实验（Dynamic simulation experiment）

为验证本文提出的具有脊柱关节的四足机器人分层控制方法的有效性，并测试所设计控制器的性能，在Webots仿真环境中搭建四足机器人模型，进行崎岖地形奔跑实验和对角步态与疾驰步态转换实验。

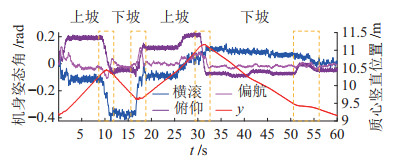
4.1 崎岖地形实验

如图 14所示，通过Webots仿真环境中内置的函数随机生成崎岖地形，四足机器人以对角步态运动，步频3 Hz，髋关节摆动幅值为$ \pi /6 $ rad。图 15为运动过程中机身姿态角和质心在竖直方向（$ y $方向）的高度变化曲线，质心的高度变化在一定程度上反映了地形的变化，可以看到机器人经历了连续的上下坡运动。在第10 s、17 s、31 s、54 s时地形坡度发生了改变，机器人俯仰角与横滚角也随坡度的改变而不断变化以调整自身姿态适应地形。偏航角在地形坡度发生改变时波动较大，其余过程均稳定在0$ ^{\circ} $附近。这表明基于VMC的姿态控制方法可以使机器人根据地形变化实时调整偏航角度，维持运动的稳定性，实现了机器人对复杂地形的适应。

图 16为在崎岖地形运动时速度的变化曲线，前向速度（$ x $方向）随地形的不同而变化，在第1次上坡运动时速度约为0.8 m/s，第1次下坡时速度高于上坡时的速度。侧向速度（$ z $方向）在第1次上坡和下坡过程中波动较大，分析其原因是地形变化较快，机器人无法立刻适应地形，消除侧向运动。第2次上坡和下坡的持续时间较长，侧向速度在0附近稳定波动，说明机器人经过一段时间调整可以适应地形，逐渐达到期望的运动。SLIP模型通过控制落足点实现速度控制，地形不平坦会影响落足点的位置，因而造成速度在整个运动过程中发生小幅度波动。

4.2 步态转换实验

利用式(20) 实现步态转换，实验中控制四足机器人先由对角步态转为疾驰步态，再转为对角步态，图 17为步态转换过程截图。图 18为步态转换过程中髋关节俯仰角度变化曲线，图 19为步态转换过程中4~7 s之间髋关节俯仰角与机身俯仰角的变化曲线。在第5 s之前机器人以对角步态运动，左、右腿相位差稳定在$ \pi $，机身俯仰角小幅波动；从第5 s开始进行对角—疾驰步态转换，左、右腿相位差逐渐减小，机身俯仰角波动也逐渐增大；在第6.25 s左、右腿相位差不再变化，步态转换完成，转换过程持续1.25 s。图 20为步态转换过程中第9~12 s之间髋关节俯仰角与机身俯仰角的变化曲线。在第9~10 s之间机器人以非对称疾驰步态稳定奔跑，左、右腿相位差稳定在$ \pi/2 $，机身俯仰角较大；从第10 s开始进行疾驰—对角步态转换，左、右腿相位差逐渐增大，机身俯仰角波动也逐渐减小；在第11.25 s左、右腿相位差不再变化，步态转换完成。整个步态转换过程平滑、自然，机器人运动平稳，验证了步态转换策略的有效性。

图 21为步态转换过程中脊柱关节角的变化曲线。在对角步态时脊柱关节角为0，脊柱关节无运动；从对角—疾驰步态转换开始，脊柱关节周期性运动，幅值随左、右腿相位差的减小而逐渐增大；在第6.25 s步态转换完成，机器人以疾驰步态运动，脊柱关节角不再变化，幅值稳定在极值附近；从进行疾驰—对角步态转换开始，幅值随左、右腿相位差的增大而逐渐减小，在第11.25 s步态转换完成，脊柱关节角不再变化。在整个步态转换过程中脊柱运动的幅值仅随左、右腿相位差的变化做差分运动，验证了脊柱—腿协调控制策略的有效性。

从图 19中还可以看到，在$ A $、$ B $点右前和右后腿相位差并非预期的$ \pi $，而是出现了差值。原因是：在$ A $点机身前倾，机身俯仰角为负，腿部执行俯仰姿态控制策略，前腿提前进入支撑相，因此前腿较后腿相位提前；在$ B $点机身后仰，机身俯仰角为正，后腿提前进入支撑相，因此后腿较前腿相位提前。脊柱相位与腿部相位相耦合，也发生一定的移相，如图 21中①所示，证明了将机体俯仰姿态角作为反馈引入CPG控制模型中，可以有效避免机身波动造成机器人倾倒，提高CPG控制的稳定性。

5 结论（Conclusion）

针对具有脊柱关节的仿猎豹四足机器人，提出了多模型融合分层运动控制架构，将SLIP模型、CPG模型、VMC模型通过有限状态机进行有机融合，并在控制方法中融入足底力与速度关联、脊柱幅值与步态映射、脊柱与腿相位耦合等动物高速运动的仿生机理，综合解决了四足机器人速度控制、姿态控制、步态控制以及地形适应性控制等复杂运动控制问题。在Webots仿真环境中实现了四足机器人在未知崎岖地形的稳定运动，实现了对称对角步态与非对称疾驰步态奔跑，以及2种步态之间的转换。研究结果证明了所提出的多模型融合的四足机器人控制方法的有效性。

多模型融合控制方法模仿了生物神经系统多功能区结构以及运动模式分类控制机理。结合SLIP模型、CPG模型和VMC模型各自的优势，分别解决复杂运动控制任务中的单腿跳跃、步态协调、环境交互等子任务，能够产生更加丰富的运动功能。与单独采用SLIP模型、VMC模型和CPG模型的四足机器人系统相比，本文提出的控制方法有以下优点：1) 具有多自由度协调控制和步态生成与转换的优势，而且整体姿态控制能力好，可以适应复杂地形；2) 与基于动力学模型的ZMP、MPC和WBC方法相比，避免了繁琐的动力学建模和解算过程，也无需在线处理大规模优化算法；3) 与智能学习方法相比，无需花费大量时间来训练模型。基于任务分解思想和仿生机理提出的多模型融合控制方法与系统架构，其算法模型简单、计算量少、对硬件要求低、易于构建低成本运动控制器，对于推进四足机器人的实用性和普及应用具有重要意义。

需要指出的是，多模型分层融合控制方法涉及大量系统参数，在应用中需要解决参数整定问题。本文目前采用的方法是人工调节（即试凑法），自底而上依次调节SLIP模型实现稳定跳跃，再调节CPG模型实现节律步态，最后调节VMC参数实现稳定的足地交互。由于各级对象模型及其控制策略在机器人运动控制架构中是分层次并解耦的，因此，单独改变某个控制策略的参数不会影响其他各层控制模型的稳定性。虽然试凑法是工程实践中常用的方法，但是当控制参数较多时，需要耗费大量人力和时间，利用优化工具或强化学习等人工智能方法解决系统参数整定是非常有潜力的发展方向。