1 引言（Introduction）

机械手作为机器人末端执行器的关键组成部分，可实现目标物体的握持操作，是机器人与周围环境进行直接交互的一个重要接口。如今，移动机器人不断兴起，轻质节能将是机器人设计的一个重要指标，而机械手作为一个重要的执行部件，在满足抓取需求的前提下还需要节能减耗。在此条件下，相比于全驱动机械手繁杂的传动和控制系统，欠驱动机械手凭借其驱动器少、传感器少、功耗低、控制系统简洁高效、自适应性强等优点更加适用于移动机器人领域。

欠驱动机械手的形式主要有腱绳式^[1-3]、连杆式^[4-7]、差动齿轮式^[8]、气动式^[9-12]等，其中，连杆式和差动齿轮式的欠驱动机械手抓取力度大，腱绳式和气动式机械手的抓取范围广。但是，目前欠驱动机械手的抓取形式单一，与全驱动机械手相同，抓取形式通常是指尖抓取或者是包络抓取。同时，这些机械手手指的某些关节是被动的，不具备驱动装置，因此具有很强的动力学耦合效应，如连杆式和腱绳式机械手，其被动关节需要通过主动关节的动力学耦合^[13-14]间接获得驱动力。尽管这种特性使得欠驱动机械手具有更好的环境自适应性^[15]，但对于以电机为驱动装置的机械手，鲜有以其他方式实现机械手的欠驱动形式和抓取形式。

为实现机械手对夹持力的控制，需要引入力的反馈闭环控制^[6]，如文[16-17]，均是通过PID（比例－积分－微分）控制器来调节电机实现对夹持力的控制，但这需要传感器的反馈和控制器的处理，设计过程中需要考虑传感器的布置和电机控制器的设计，会增加机械手控制的复杂程度。另外一种可实现夹持力调节的是气动机械手，这种机械手通过气压来调节手指的抓取力度，如气动柔性五指机械手^[12]和气动肌腱欠驱动机械手^[3]，体现了气动机械手可通过气体调节手指位姿和夹持力大小的特点，而唯一的缺点在于机械手需要一个气泵为其提供不同压强的气体。

本文根据目前欠驱动机械手抓取形式单一和无法实现夹持力控制的问题，设计了一种基于行星齿轮机构的欠驱动机械手。机械手采用一种同时不固定输出轴和内齿圈的行星齿轮机构来分配2种驱动扭矩：一种用于机械手手指的关节转动，以实现对目标物体的夹持；另一种用于皮带的转动，以实现对目标物体的牵引。通过皮带的牵引形式来拉入目标物体，实现一种新的目标物体抓取形式，使得机械手不仅可以夹持物体，还能够牵引拉入物体。根据行星齿轮机构单输入双输出的特点，创新地设计了阻力矩调节机构，在没有力传感器反馈的条件下实现了机械手的夹持力调节功能。

2 机械手的结构设计（Structure design of the manipulator） 2.1 机械手的手指结构设计

机械手是直接与目标物体接触的部分，起着夹持并拉入目标物体的作用。单个手指的结构如图 1所示，蜗杆1和蜗轮1控制关节1的转动，利用平行四边形结构，在转动指的带动下，抓取指平稳闭合，实现对目标物体的夹持功能；蜗杆2和蜗轮2传递的动力通过齿轮传动并带动皮带运动，实现对目标物体的拉入功能。从图 1中的传动关系可以看到，手指的转动关节1和同步带的转动之间并不存在耦合关系，这是与连杆式和腱绳式机械手手指的不同之处。动力传递过程中，采用蜗轮蜗杆，一方面实现动力的传递，另一方面利用蜗轮蜗杆的自锁能力，在电机停止运转后防止手指松开，同时也防止被拉入的目标物体在重力作用下回落。

根据文[18-19] 可知，负载对皮带的动态特性有一定的影响，对于皮带拉入式的手指结构，需要设计皮带预紧机构或者提供足够的支撑点，使皮带有足够的张紧力。文[5, 8] 中提出的皮带拉入式机械手就存在皮带张紧力不足和少支撑点的情况，这使得这类机械手只能抓取小质量物体。针对图 1中的手指，为了避免目标物体在拉入过程中由于皮带张紧力的不足而缺乏支撑，设计了由弹簧相连接的张紧轮1和张紧轮2，这2个张紧轮在提供2个支撑点保证稳定抓取的同时还能延长皮带的寿命。

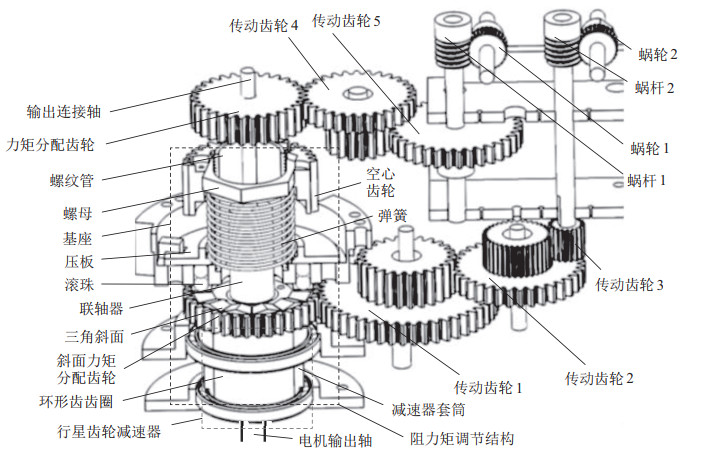
2.2 机械手的传动结构设计

通常，采用电机为动力的欠驱动机械手，往往是利用动力学耦合效应实现机械手的欠驱动形式，而本文采用行星齿轮减速器来分配2种驱动扭矩以实现机械手的欠驱动形式，其传动结构如图 2所示。

传动结构主要分阻力矩调节机构和齿轮传动两部分，从图 2中可看出行星齿轮减速器的内齿圈和输出连接轴并未固定，因此可输出2种互斥的运动，其中，输出轴作为第一输出，内齿圈作为第二输出。联轴器将输出连接轴和行星齿轮减速器的输出轴固定在一起，通过力矩分配齿轮将动力传递至蜗杆1和蜗轮1，实现图 1中关节1的转动；斜面力矩分配齿轮和行星齿轮减速器的内齿圈固定，将动力传递至蜗杆2和蜗轮2，实现图 1中皮带的转动。

利用行星齿轮结构可分配2种互斥运动的特点，在输出轴和内齿圈之间嵌入一个阻力调节机构，在一定的范围内，通过调节阻力矩的大小可以间接调节机械手手指夹持目标物体的力度。阻力矩调节机构的原理是：空心齿轮顺时针转动，带动固定于其上的螺母在螺纹管上进行螺旋运动，螺旋运动迫使空心齿轮向下移动进而压缩弹簧，增大施加在压板上的弹力，这种弹力会通过滚珠施加在斜面力矩分配齿轮的三角斜面上。斜面力矩分配齿轮和内齿圈相对固定，滚珠作用在三角斜面的分力所产生阻力矩会直接作用在内齿圈上，增大内齿圈所受的总阻力矩。

行星齿轮机构传动原理和2个力矩分配齿轮的连接示意图如图 3所示，斜面力矩分配齿轮和内齿圈相对固定，力矩分配齿轮和输出轴相对固定。

机械手在单个电机输入的情况下，能够输出2个运动，分别控制机械手手指的闭合和皮带的转动。在抓取过程中，电机启动，由于内齿圈受到的总阻力矩大于输出轴受到的总阻力矩，因此输出轴通过传动部件使机械手手指闭合直至夹紧目标物体，此时输出轴受到的总阻力矩增大直至超过内齿圈受到的阻力矩，于是内齿圈带动斜面力矩分配齿轮转动，并带动皮带运转拉入被夹持住的目标物体。

机械手采用这种传动系统和手指结构，利用行星齿轮结构可分配2种互斥运动的特点，将多自由度的控制从手指端转移到驱动端，减弱了手指运动中的动力学耦合效应。而设计的阻力调节机构，在一定的范围内，可间接调节机械手手指夹持目标物体的力度，从而进一步减少传感器数目和降低电机的控制复杂程度。

值得注意的是，本文采用皮带接触和皮带拉入目标物体的形式，一方面皮带接触不会损坏物体，使机械手可以抓取柔性目标物体，如纸杯、鸡蛋等；另一方面机械手手指抓取住目标物体之后就会拉入物体，而同步带轮做无限旋转运动，避免了电机发生堵转的情况。因此，相比于其他类型的欠驱动机械手，本文设计的机械手的柔性更好，抗外界冲击能力更强。

3 运动学和静力学（Kinematics and statics） 3.1 运动学分析

所设计的欠驱动机械手手指采用三指圆周分布，三指机械手抓取圆形目标物体的时候，会有3个接触面，根据手指抓取顺序，这里给出其中一个平面空间的手指抓取受力分析图，如图 4所示。

图 4左侧是机械手手指张开状态的受力分析图，图 4右侧是机械手手指闭合并夹紧目标物体状态的受力分析图。将图 1中的关节1设定为坐标原点$ O $，并建立平面坐标系$ XOY $，$ \theta $为关节1的转动角度，$ l_{i} $（$ i= 1, 2, 3, 4 $）分别为$ OE $、$ ED $、$ EB $、$ DP_{0} $段的长度，其中AOBE是平行四边形。

在机械手抓取到目标物体之前，以图 4左侧中单指垂直抓取为例，可得出指尖$ P_{0} $在$ XOY $坐标系中的坐标为

$ \begin{align} \begin{bmatrix} P_{0x} \\ P_{0y} \end{bmatrix}= \begin{bmatrix} l_{1} \cos \theta -l_{2} \\ l_{1} \sin \theta + l_{4} \end{bmatrix} \end{align} $

(1)

式中，$ P_{0x} $为指尖$ P_{0} $在$ XOY $坐标系中的横轴坐标，$ P_{0y} $为指尖$ P_{0} $在$ XOY $坐标系中的纵轴坐标。机械手的3根手指呈圆周分布，$ C $为中心点，$ R $为3根手指分布的圆周半径，不考虑皮带在夹持力作用下的形变，3根手指张开半径$ W $为

$ \begin{align} W=P_{0x} +R=l_{1} \cos \theta -l_{2} +R \end{align} $

(2)

关节1的转动角度$ \theta $的范围受到转动指的约束，对式(1) 中的$ \theta $进行微分可得指尖$ P_{0} $的速度为

$ \begin{align} \mathit{\boldsymbol{V}}_{P_{0}} = \begin{bmatrix} -l_{1} \sin \theta \\ l_{1} \cos \theta \end{bmatrix} \dot{\theta} \end{align} $

(3)

机械手的皮带在接触到目标物体之后不会立即拉入物体，而是在夹持力作用下，皮带发生弹性变形。当皮带开始拉入物体之后，由于失去了同步带轮对皮带的支撑，即使是有张紧轮的辅助支撑，皮带也会在夹持力的作用下产生更大的变形以保证所需的张紧力，此时手指的位姿也会发生改变。如图 4(b)所示，机械手接触并夹紧目标物体，随着目标物体被皮带拉入，最初接触点$ P $的坐标为

$ \begin{align} \begin{bmatrix} P_{x} \\ P_{y} \end{bmatrix}= \begin{bmatrix} l_{1} \cos \theta -l_{2} +l_{\Delta} \\ l_{1} \sin \theta +l \end{bmatrix} \end{align} $

(4)

式中，$ l_{\Delta} $为皮带在夹持力作用下的形变，$ l $为手指夹持住目标物体时接触点$ P $到点$ D $之间的距离。

3.2 静力学分析

针对机械手手指夹紧目标物体之后、皮带拉入目标物体之前的情形，对手指进行静力平衡分析，以描述输入的关节扭矩和夹持力之间的关系。根据虚功原理^[20]，由图 4可以得到

$ \begin{align} \tau =F_{x} l_{1} \sin \theta -F_{y} l_{1} \cos \theta \end{align} $

(5)

式中，$ \tau $为手指的输入扭矩，由蜗轮蜗杆提供，$ F_{x} $和$ F_{y} $分别表示在$ X $轴和$ Y $轴方向上指尖接触点处的力。在此平衡状态下，假设机械手的3个手指完全夹紧目标物体，不考虑皮带弹性变形和手指的挠度，手指施加在目标物体上的力$ F_{x} $即为夹持力，纵轴方向的力$ F_{y} =\dfrac{1}{3}mg $，$ m $为目标物体的质量，$ g $为重力加速度。

3.3 阻力矩调节机构分析

对于传统机械手，夹持力的调节主要依靠对驱动电机的控制，而这个过程中，力传感器的使用是不可或缺的。这类机械手不仅需要使用多个传感器，而且还需要复杂的闭环控制系统才能实现机械手位姿和夹持力的控制。为了减少传感器的使用和简化控制系统，所设计的欠驱机械手利用行星齿轮能够分配2种互斥运动的特点，创新地设计了阻力矩调节机构，使机械手不需要传感器，不需要闭环控制，也不需要直接控制驱动电机，就能实现对夹持力的调节，其原理如图 5所示。

在电机的输入扭矩下，行星减速器的输出轴扭矩$ T_{\rm a} $和内齿圈输出的扭矩$ T_{\rm b} $是相等的。其中，输出轴扭矩和机械手阻力矩的关系为

$ \begin{align} \begin{cases} T-T_{\rm f0} =T_{\rm a} =T_{\rm af} \\ T_{\rm af} =\sum T_{\rm f1} +\tau \end{cases} \end{align} $

(6)

式中，$ T $为电机输出的扭矩，$ T_{\rm f0} $为行星齿轮减速器内部的阻力矩，$ T_{\rm af} $为输出轴所受的总阻力矩，$ \sum T_{\rm f1} $为输出轴到手指之间齿轮啮合传动时的阻力矩。同理，可得内齿圈扭矩和机械手阻力矩的关系为

$ \begin{align} \begin{cases} T-T_{\rm f0} =T_{\rm c} =T_{\rm cf} \\ T_{\rm cf} =\sum T_{\rm f2} +T_{\rm ad} +T_{\rm sw} \end{cases} \end{align} $

(7)

式中，$ T_{\rm cf} $为内齿圈所受的总阻力矩，$ \sum T_{\rm f2} $为内齿圈到皮带传动所产生的阻力矩之和；$ T_{\rm ad} $为阻力矩调节机构产生的阻力矩，$ T_{\rm sw} $为同步带轮输出扭矩。

根据行星减速器传动的特点，可以得出行星齿轮减速器输出轴和内齿圈的转动取决于各自所受的阻力矩大小，在电机输入扭矩一定的情况下，按照机械手抓取目标物体的顺序，可得：

① 电机启动，$ T_{\rm af} <T_{\rm cf} $，内齿圈阻力矩大于输出轴阻力矩，输出轴转动，机械手手指闭合。

② 机械手手指闭合并夹紧目标物体时，$ T_{\rm af} =T_{\rm cf} $，内齿圈阻力矩等于输出轴阻力矩，机械手处于平衡状态，有$ \sum T_{\rm f1} =\sum T_{\rm f2} =T_{\rm sw} =0 $。

③ $ T_{\rm af} >T_{\rm cf} $，输出轴阻力矩大于内齿圈阻力矩，内齿圈开始转动并带动皮带拉入被夹持住的目标物体。

阻力矩调节机构中，如图 5所示，螺母跟随空心齿轮一起在空心螺纹管中转动，在转动过程中，螺母和空心齿轮向下移动并压缩弹簧，弹簧弹力为

$ \begin{align} F_{\rm s} =\phi \frac{p}{2{\pi}} k \end{align} $

(8)

式中，$ \phi $为空心齿轮的角位移，$ p $为空心螺纹管的导程，$ k $为弹簧弹性系数。弹簧施加的弹力$ F_{\rm s} $会通过滚珠施加到斜面力矩分配齿轮的三角斜面上，因此，阻力调节机构提供的阻力矩$ T_{\rm ad} $为

$ \begin{align} T_{\rm ad} =\frac{d}{2}F_{\rm s} \tan \alpha =\phi \frac{pdk\tan \alpha} {4\pi} \end{align} $

(9)

式中，$ d $为滚珠与三角斜面接触点的圆直径，$ \alpha $为三角斜面的倾角。

根据结论②，有$ T_{\rm af} =T_{\rm cf} $，$ \sum T_{\rm f1} =\sum T_{\rm f2} =T_{\rm sw} $ $ =0 $，于是可得

$ \begin{align} \begin{cases} \sum T_{\rm f1} +\tau =\sum T_{\rm f2} +T_{\rm ad} +T_{\rm sw} \\ \tau =T_{\rm ad} \end{cases} \end{align} $

(10)

由式(5)可以得到在扭矩$ \tau =T_{\rm ad} $下，夹持力$ F_{x} $为

$ \begin{align} F_{x} & =\frac{T_{\rm ad}} {l_{1} \sin \theta} +\frac{1}{3}mg\cot \theta \\ & =\phi \frac{pdk\tan \alpha} {4{\pi} l_{1}} \frac{1}{\sin \theta} +\frac{1}{3}mg\cot \theta \end{align} $

(11)

其中，参数$ p $、$ d $、$ k $、$ \alpha $、$ l_{1} $均为常量，令

$ \begin{align} K=\frac{pdk\tan \alpha} {4\pi l_{1}} \end{align} $

(12)

式中，$ K $为力矩调节系数，可得夹持力$ F_{x} $为

$ \begin{align} F_{x} =\phi \frac{1}{\sin \theta} K+\frac{1}{3}mg\cot \theta \end{align} $

(13)

从式(13)中可以看出夹持力$ F_{x} $与空心齿轮角位移、目标物体的大小及其重量相关，但是在抓取一个不定直径、不定重量的目标物体时，完全可以通过控制空心齿轮的角位移来调节夹持力的大小。在设计指标中，采用的压缩弹簧弹性系数是确定的，提供的弹力也是有限的，而空心齿轮存在极限转动角位移，对于一个固定大小的目标物体，要在空心齿轮的极限角位移处继续增大夹持力，可采用弹性系数更大的压缩弹簧。

4 实验（Experiment）

为了清晰看到机械手动力传递的整个过程，欠驱动机械手样机大部分采用的是透明亚克力板和树脂材料。欠驱动机械手样机如图 6所示。

阻力矩调节机构的各个参数如表 1所示。

4.1 夹持力测试实验

通过力学分析，机械手的夹持力与阻力矩调节机构的空心齿轮角位移和目标物体大小及其重量相关。为了消除其他因素的干扰，探究阻力矩调节机构与机械手夹持力之间的关系，实验时，取一个定直径的目标物体，测试空心齿轮在不同角位移下的夹持力大小。这个测试方案中需要控制空心齿轮的角位移，为此，测试实验设置了光电开关和码盘，用于检测真实的角位移，空心齿轮则通过减速电机进行驱动，如图 7所示。

机械手夹持力测试实验如图 8所示，实验平台为NI PXI-042Q，采用LabVIEW编程，通过NI PXI-6259模块实现信号的输出和数据的采集。

测试夹持力时采用电阻式薄膜压力传感器，其量程为0.5~20 N，将其贴在目标物体上，然后利用专用的电阻－电压转换模块将传感器的电阻信号转换为模拟电压信号，就可测试出机械手手指的夹持力。实验抓取的目标物体为一个圆柱形砝码，其质量为500 g，直径为38 mm，高度为61 mm。为了便于测试夹持力，将圆形皮带更换为平面皮带进行测试。

实验时，设计空心齿轮每次转动角度为60$ ^{\circ} $，然后采集电阻－电压转换模块输出的电压信号，将采集的数据进行整理并提取出来，手指的夹持力$ F_x $和空心齿轮角位移$ \phi $的关系如图 9所示。

从图 9可知，空心齿轮角位移为0时，夹持力约为0.5 N，空心齿轮角位移为900$ ^{\circ} $时，夹持力约为20 N。通过曲线图可以直观看出，机械手手指夹持力随着空心齿轮角位移的增大而增大，验证出阻力矩调节结构能够有效调节机械手的夹持力。

4.2 抓取实验

在抓取实验中，令机械手抓取不同材料的目标物体，以检验其有效性，这些目标物体的具体参数如表 2所示。

机械手夹持并拉入目标物体的实验结果如图 10所示。

为了达到实验目的，抓取的目标物体中包含了铁杯、砝码一类的刚性物体，也包含了纸杯、围巾一类的柔性物体。对于刚性目标物体，在合适的夹持力下，机械手能顺利且稳定地实现夹持和拉入操作。对于柔性目标物体，如图 10(b)(i)所示，抓取空水瓶和空纸杯时，通过阻力矩调节机构减小了夹持力，在机械手夹持并稳定拉入的过程中，并没有破坏空水瓶和空纸杯的外形，表现出该机械手具备良好的柔顺性。通过抓取不同材料的目标物体，可以看出该机械手具有稳定的抓取能力和拉入能力，体现出其良好的适应性。

5 结论（Conclusion）

设计了一种基于行星齿轮机构的牵引式拉入欠驱动机械手，机械手手指呈圆周分布，适合抓取刚性和柔性目标物体。该机械手最明显的优势如下：

(1) 利用行星齿轮机构，实现了2种互斥运动的输出，并根据这种特点，设计了阻力矩调节机构，在没有传感器和力反馈的条件下实现了对夹持力的调节。

(2) 利用皮带的牵引作用，机械手不仅有夹持的功能，还有拉入功能，提供了一种新的抓取形式。同时，机械手既能抓取刚性物体，也能抓取柔性物体。

(3) 整机的控制系统简单，同步带轮的无限旋转运动使电机不会发生堵转的情况。

通过夹持力测试实验，得出阻力矩调节机构的夹持力调节范围约为1~20 N，验证了阻力矩调节机构的有效性。抓取实验表明，本文设计的欠驱动机械手完全能够在预期的设计目标下实现对刚性和柔性目标物体的夹持与拉入操作，体现了机械手针对不同目标物体的适应性和柔顺性。