2. 上海市智能制造及机器人重点实验室, 上海 200444;
3. 上海大学人工智能研究院, 上海 200444;
4. 江苏省先进机器人技术重点实验室, 江苏 苏州 215123;
5. 上海航天控制技术研究所, 上海 201109;
6. 上海市空间智能控制技术重点实验室, 上海 201109
2. Shanghai Key Laboratory of Intelligent Manufacturing and Robotics, Shanghai 200444, China;
3. School of Artificial Intelligence, Shanghai University, Shanghai 200444, China;
4. Jiangsu Province Key Laboratory of Advanced Robot Technology, Suzhou 215123, China;
5. Shanghai Aerospace Control Technology Institute, Shanghai 201109, China;
6. Shanghai Key Laboratory of Aerospace Intelligent Control Technology, Shanghai 201109, China
随着机器人技术的智能化与机械臂在各行业中更广泛的应用,机械臂需要能够适应非结构化的工作环境。在该类环境中,常有意料外的障碍物阻挡在机械臂的原工作路径上,因此,机械臂的避障路径规划是一个有意义的研究方向。
机械臂实现避障路径规划的前提是,机械臂需要准确、可靠地感知到障碍物,即障碍物的目标检测问题。目前,主流的目标检测方法都是基于视觉的,并且随着深度学习的发展,已有许多学者针对结合视觉与深度学习的目标检测算法进行了大量研究[1-3],并且不少学者将其应用于机械臂上,如完成抓取任务[4-6]、在复杂环境中实现多物体的识别、分拣[7]以及可视化[8]。
然而,基于视觉的方法往往容易出现遮挡问题,相对应地,Tsuji等[9]设计了一种可扩展的接近觉传感器模块。受文[9] 启发,本文提出了基于接近觉的障碍物感知方法,该方法将接近觉传感器阵列布置在机械臂连杆上以感知障碍物。当机械臂感知到障碍物后,需要使用合理的路径规划方法规划避障路径,其可分为全局方法与局部方法。其中,前者适用于环境信息已知的情况,包括A* 算法[10]、C空间法[11]、栅格法[12]和快速扩展随机树法[13-14]等;后者适用于环境信息未知的情况,包括人工势场法[15]、遗传算法[16]和神经网络算法[17]等。基于李娜[18]采用的适用于机械臂的基于势函数与关节空间的人工势场法,并结合基于接近觉的障碍物感知方法,本文进一步提出了基于接近觉的机械臂避障路径规划方法,并在UR10小臂连杆上进行了验证。与较为常见的基于视觉的方法相比,该方法可以避免视觉遮挡问题,并且接近觉传感器响应迅速、得到的数据量非常小、易于处理。
本文的主要贡献与创新为:1) 提出了假想圆锥与安全平面的概念,实现了有效的基于接近觉的机械臂障碍物感知;2) 提出了连杆运动方向的概念,优先读取该方向上的接近觉传感器,降低传感器读取周期、提升算法实时性与传感器阵列的扩展潜力;3) 考虑到所提出避障方法的特点,提出了基于人工势场法的改进的绕行法,使得机械臂在避障过程中得以逃离局部最优陷阱。
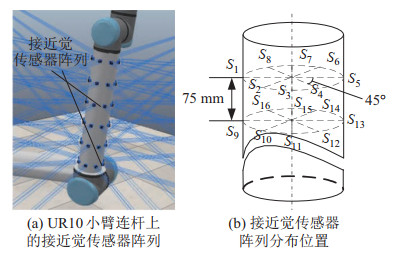
2 基于接近觉的机械臂障碍物感知(Obstacle perception by the manipulator based on proximity) 2.1 接近觉传感器阵列分布本文在UR10机器人小臂上安装接近觉传感器阵列以验证所提出的避障方法,如图 1所示。阵列以6个间隔为75 mm的圆周的方式均匀对称分布,每个圆周上以45
|
图 1 接近觉传感器阵列分布 Fig.1 Distribution of proximity sensor array |
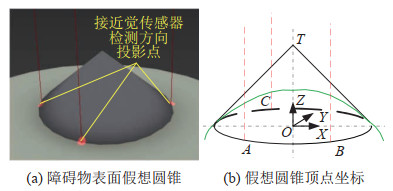
假设障碍物表面封闭且连续,则接近觉传感器阵列会以一系列投影点的距离信息的形式,在其检测方向上感知到障碍物表面,并且可以从中找出距离连杆表面最近的点。然而,检测到的最近投影点未必就是障碍物离连杆实际最近的点,在传感器间隙处障碍物的局部表面还可能存在凸起的特征。因此考虑将投影距离最近的相邻的3个传感器之间的障碍物局部表面构造为一个假想的顶角一定的圆锥。并且将该圆锥的顶点作为障碍物表面离连杆表面距离最近的危险点,假想圆锥顶角的设定会对机械臂连杆与障碍物表面间的距离产生影响,当设定该假想圆锥顶角为90
如图 2所示,点
|
图 2 障碍物局部表面建模 Fig.2 The modeling of obstacle local surface |
设
| $ \begin{align} \begin{bmatrix} {x_{T}} \\ {y_{ T}} \\ {z_{ T}} \end{bmatrix}=\mathit{\boldsymbol{v}}\cdot t+\begin{bmatrix} {x_{0}} \\ {y_{0}} \\ {z_{0}} \end{bmatrix} \end{align} $ | (1) |
其中,
| $ \begin{align} \mathit{\boldsymbol{v}} & =\begin{bmatrix} {x_{2} -x_{1}} \\ {y_{2} -y_{1}} \\ {z_{2} -z_{1}} \end{bmatrix} \begin{bmatrix} {x_{3} -x_{1}} \\ {y_{3} -y_{1}} \\ {z_{3} -z_{1}} \end{bmatrix} \end{align} $ | (2) |
| $ \begin{align} t & =\pm \frac{d^{2}}{ | \mathit{\boldsymbol{v}} | } \end{align} $ | (3) |
| $ \begin{align} d & =\frac{r}{ \tan \dfrac{\theta} {2}} \end{align} $ | (4) |
需要注意的是,
由于传感器数量较多,在一个控制周期内轮询全部传感器难以满足算法的实时性,限制了进一步增加传感器数量的升级潜力。因此,本节定义了连杆的运动方向,在一个控制周期内优先读取该方向上的传感器,并在空闲周期轮询剩余传感器。
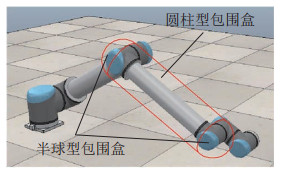
机械臂的连杆可采用包围盒的方法进行简化,图 3所示为UR10小臂的包围盒简化图,对于简化后的连杆来说,其绕着自身轴线旋转的并不是与障碍物发生碰撞的主要自由度,因此将连杆的运动简化为包围盒轴线段的运动。于是,定义连杆的运动方向为轴线段2个端点的空间平移方向,此时在轴线段上的所有点在空间中的运动也全部确定。
|
图 3 UR10小臂包围盒 Fig.3 Bounding box of an UR10's forearm |
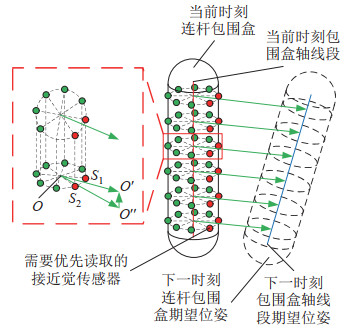
如图 4所示,红色线段表示连杆包围盒轴线段,代表连杆包围盒在当前空间中的姿态,蓝色线段代表在一个时间步
|
图 4 连杆运动方向上的接近觉传感器 Fig.4 Proximity sensors in the movement direction of a link |
接近觉传感器阵列无法同视觉传感器、激光雷达传感器等一样相对完整、精确地获取障碍物的空间信息。因此,考虑构造安全平面以对连杆的运动进行约束,使连杆包围盒不能与其发生碰撞。显然,只要包围盒两端点同时与安全平面保持在安全距离外即可满足约束,易于实现。
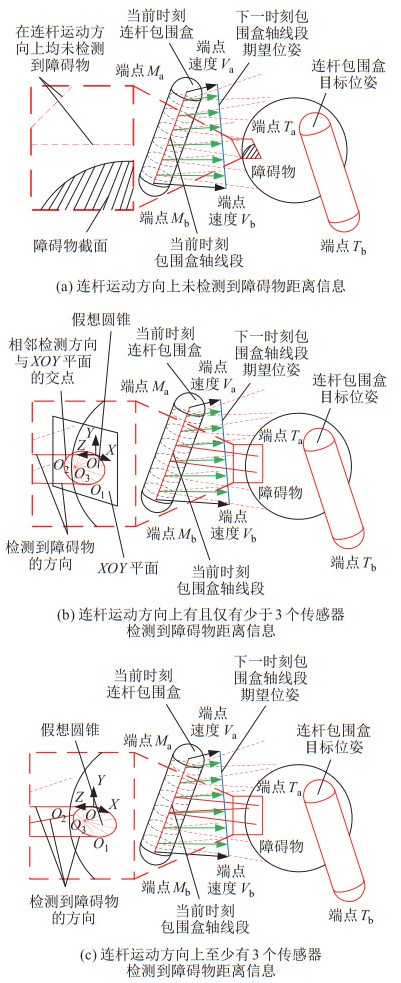
部署了接近觉传感器阵列的机械臂连杆在空间中运动,并采用2.3节的方法读取该连杆运动方向上的传感器,在此过程中,机械臂对障碍物的感知共分为图 5所示的3种情形。图 5(a)中连杆的运动安全不受限;图 5(b)中有且仅有少于3个传感器的投影距离信息,此时采取如下步骤构造假想圆锥:1) 选取距离最近的投影点
|
图 5 机械臂障碍物感知的情形 Fig.5 Cases of obstacle perception by the manipulator |

|
图 6 安全平面的建立 Fig.6 Building of the safety plane |
所提出的基于接近觉的机械臂障碍物感知方法将障碍物简化为一个安全平面,实现了基于接近觉的机械臂障碍物感知。连杆需要到达目标位姿,而连杆与目标位姿间存在将其分割开的安全平面。连杆在运动过程中安全平面会改变,当连杆在其运动方向上的安全平面消失时,连杆可以在避开障碍物的同时到达目标位姿。
3 基于接近觉的机械臂避障路径规划(Obstacle avoidance path planning of manipulator based on proximity) 3.1 基于接近觉的人工势场法在基于接近觉的机械臂障碍物感知方法能够准确感知障碍物后,需要合理的路径规划方法以最终实现避障。因此,需要一种高效且适用于环境未知的局部路径规划方法,该方法能够适应安全平面并随着机械臂的运动而发生变化。综合上述考虑,本文采用人工势场法进行机械臂的避障路径规划。
人工势场法在移动机器人路径规划中得到了广泛应用,而不能简化为质点的机械臂的路径规划问题则更为复杂,人工势场法需要加以改进才能应用。本文基于前文提出的障碍物感知方法,采用文[18] 中基于势场函数与关节空间的人工势场法构造机械臂的引力势能
| $ \begin{align} U_{\rm{att}} ({{\mathit{\boldsymbol{\varTheta}}}_{t}})=\frac{1}{2}\zeta \rho^{2}({{\mathit{\boldsymbol{\varTheta}}}_{t}, {\mathit{\boldsymbol{\varTheta}}}_{\rm{goal}}})+k|{\mathit{\boldsymbol{\varTheta}}}_{t} -{\mathit{\boldsymbol{\varTheta}}}_{t-1} | \end{align} $ | (5) |
其中,
| $ \begin{align} &U_{\rm{rep}} ({{\mathit{\boldsymbol{\varTheta}}}_{t}})=\\ &\begin{cases} \frac{1}{2}\eta \left({\frac{1}{\min({d_{\rm a} ({{\mathit{\boldsymbol{\varTheta}}}_{t} | \mathit{\boldsymbol{P}}}), d_{\rm b} ({{\mathit{\boldsymbol{\varTheta}}}_{t} | \mathit{\boldsymbol{P}}})})-r}-\frac{1}{d_{0}}}\right)^{2}, \\ \quad \quad 0<\min({d_{\rm a} ({{\mathit{\boldsymbol{\varTheta}}}_{t} | \mathit{\boldsymbol{P}}}), d_{\rm b} ({{\mathit{\boldsymbol{\varTheta}}}_{t} | \mathit{\boldsymbol{P}}})})-r\leqslant d_{0} \\ 0, \quad\rm{其他} \end{cases} \end{align} $ | (6) |
其中,
| $ \begin{align} U({{\mathit{\boldsymbol{\varTheta}}}_{t}})=U_{\rm{att}} ({{\mathit{\boldsymbol{\varTheta}}}_{t}})+U_{\rm{rep}} ({{\mathit{\boldsymbol{\varTheta}}}_{t}}) \end{align} $ | (7) |
在某时刻下,机器人关节
| $ \begin{align} U({{\mathit{\boldsymbol{\varTheta}}}_{t}^{*}})=\min\limits_{{\mathit{\boldsymbol{\varTheta}}}_{t} \in A_{{\mathit{\boldsymbol{\varTheta}}}}} \{{U({{\mathit{\boldsymbol{\varTheta}}}_{t}})}\} \end{align} $ | (8) |
事实上,对于一般的6自由度机械臂,第1、2、3关节对其避障起主要作用,为了提高算法的实时性,在实验中仅搜索1、2、3关节角组合即可。
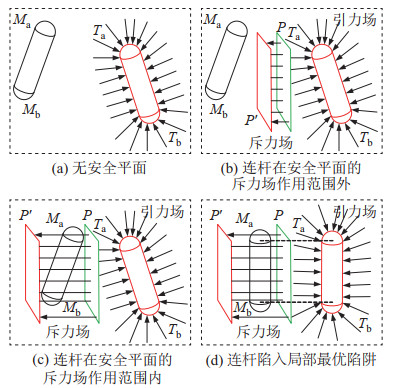
3.2 基于绕行法的改进算法当构造了3.1节中的引力场与斥力场后,连杆、安全平面以及目标位姿的空间关系如图 7所示。由图 7(d)可知,人工势场法陷入了局部最优陷阱,此时有:
| $ \begin{align} U({{\mathit{\boldsymbol{\varTheta}}}_{t}^{*}})=U({{\mathit{\boldsymbol{\varTheta}}}_{t-1}}) \end{align} $ | (9) |
|
图 7 人工势场法中连杆、安全平面与连杆目标位姿的关系 Fig.7 The relationship among link, safety plane and target pose of a link in artificial potential field method |
即此时任何关节角组合都不能使连杆总势能下降。
人工势场法局部最优问题已有许多种改进方法[19-21]。但当平面障碍物在空间中可无限延伸且会随着连杆运动而变化时,常规改进方法难以确保算法不重新陷入局部最优陷阱。
本文假设障碍物表面是连续且封闭的,受文[22] 中的移动机器人沿墙导航法的启发,提出了基于绕行的机械臂人工势场改进方法,当连杆沿着障碍物表面向一个方向绕行时,最终连杆必定可以避开阻挡在路径上的障碍物并到达其目标位姿。对于人类来说,当有障碍物挡在小臂前时,可以灵活地转动其肘关节躲避障碍物,因此可以定义机械臂连杆的绕行为:当连杆
| $ \begin{align} U_{\rm{att}} ({{\mathit{\boldsymbol{\varTheta}}}_{t}})=\;&\frac{1}{2}\zeta_{1} \sum\limits_ {i\ne m} ({\theta_{it} -\theta_{{\rm{goal}}\_i}})^{2} \pm \zeta_{2} \theta_{m_{t}} + \\ & k|{\mathit{\boldsymbol{\varTheta}}}_{t} -{\mathit{\boldsymbol{\varTheta}}}_{t-1} | \end{align} $ | (10) |
其中,
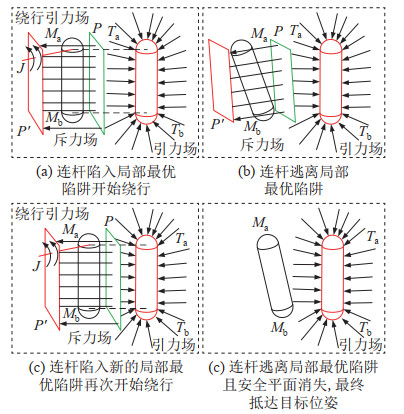
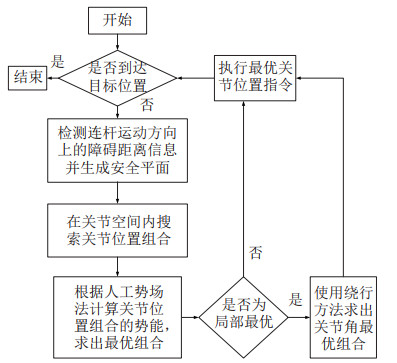
如图 8所示,在上述绕行时的引力场与斥力场的共同作用下,连杆在避开障碍物的同时能离开局部最优陷阱,最终到达目标位姿。所提出的避障算法流程图如图 9所示。
|
图 8 绕行法逃离局部最优陷阱 Fig.8 Escaping the local optimum trap by the detour method |
|
图 9 算法流程图 Fig.9 Algorithm flow chart |
采用图 10所示的TOF(飞行时间)传感器组成如2.1节中所述的阵列,并部署于UR10机器人的小臂连杆上用于接近觉感知与测距,通过串口轮询完成数据读取。为便于传感器阵列的安装、固定与拆卸,设计了如图 11所示的外壳,该外壳采用3D打印制造。将TOF传感器安装在壳体上并接通电源与串行总线。由于实验对传感器的安装精度要求不高,因此安装后无需标定。实验采用Python语言编写程序,PC上位机端通过串口读取TOF传感器阵列的距离数据,并采用全双工的TCP/IP协议与UR10机器人控制器进行网络通信,实现UR10机械臂的控制和其关节位置信息的读取。实验控制系统如图 12所示。TOF传感器单个读取周期最快可达1 ms,采用2.3节中所述的轮询方法后,一个控制周期需优先读取12个传感器,即需要12 ms,UR10机器人上位机的收发数据通信周期为8 ms,但考虑到后续工作中传感器阵列的扩展潜力以及需要留有足够的空闲周期轮询所有传感器,因此将控制周期设为80 ms,足够满足实时性即可。

|
图 10 实验用TOF传感器 Fig.10 The TOF sensor used in the experiment |

|
图 11 传感器固定壳体 Fig.11 Sensor fixing housing |

|
图 12 实验控制系统 Fig.12 Control system in the experiment |
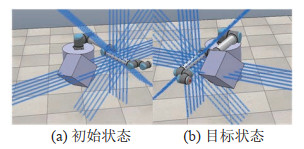
实验中UR10机器人平放于水平面,初始状态到目标状态需要其基座关节顺时针摆过60
|
图 13 UR10机器人设置示意图 Fig.13 Setting of the UR10 robot |

|
图 14 球体、圆柱体、长方体障碍物 Fig.14 Spherical, cylindrical and rectangular obstacles |
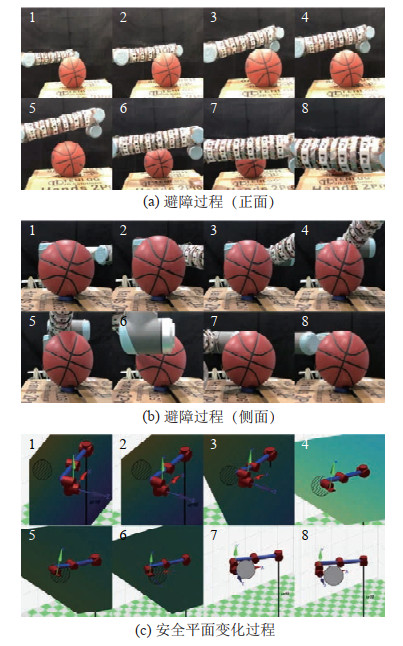
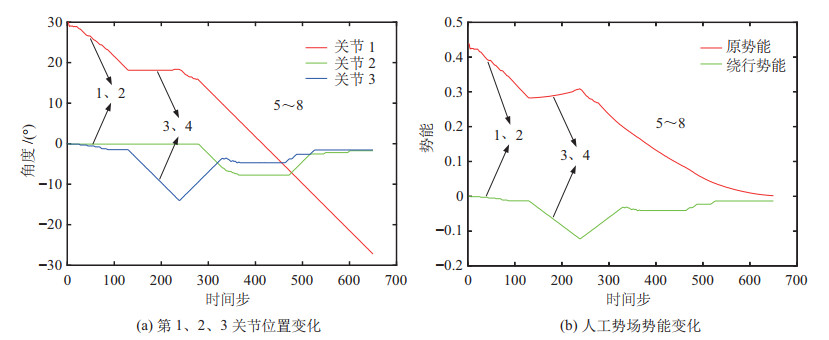
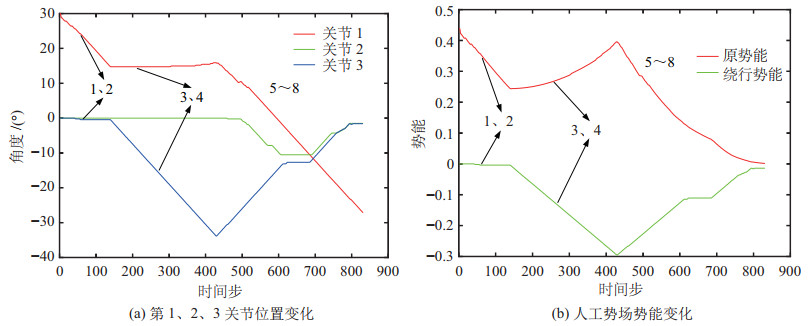
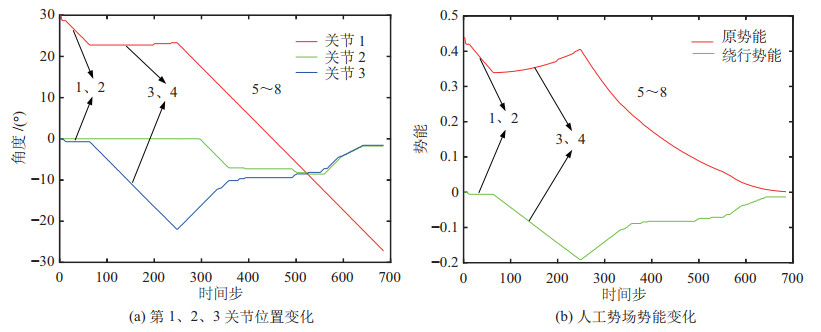
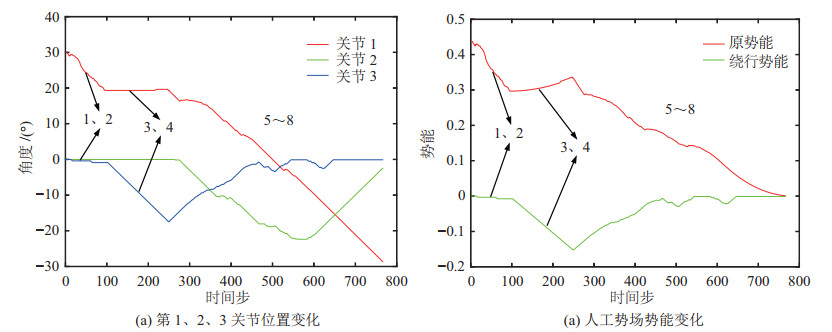
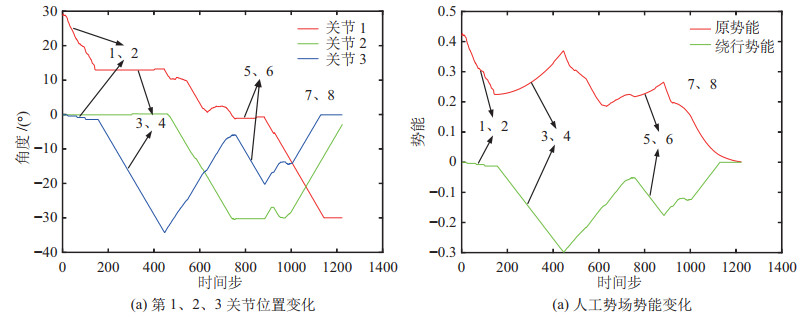
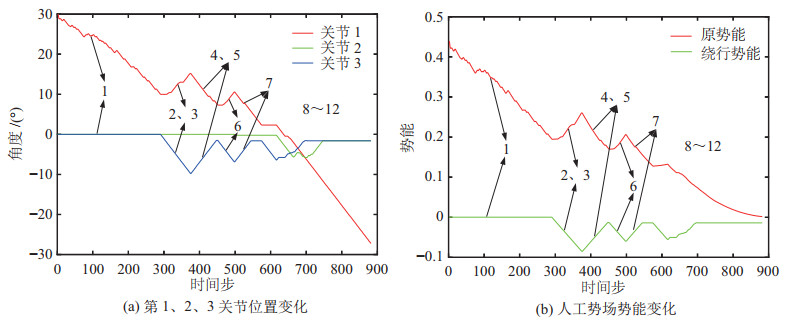
实验过程分别如图 15~图 20所示,图 21~图 26展示了算法中参与关节角组合搜索的第1、2、3关节的角度位置变化与人工势场法的势能变化,图 21~图 26(b)中红色曲线表示原势能曲线、绿色曲线表示绕行时的势能曲线。
|
图 15 球体障碍物避障实验 Fig.15 The experiment of avoiding spherical obstacle |

|
图 16 圆柱体障碍物避障实验 Fig.16 The experiment of avoiding cylindrical obstacle |

|
图 17 长方体障碍物避障实验 Fig.17 The experiment of avoiding rectangular obstacle |

|
图 18 背包与圆柱体障碍物避障实验 Fig.18 The experiment of avoiding bag and cylindrical obstacle |
|
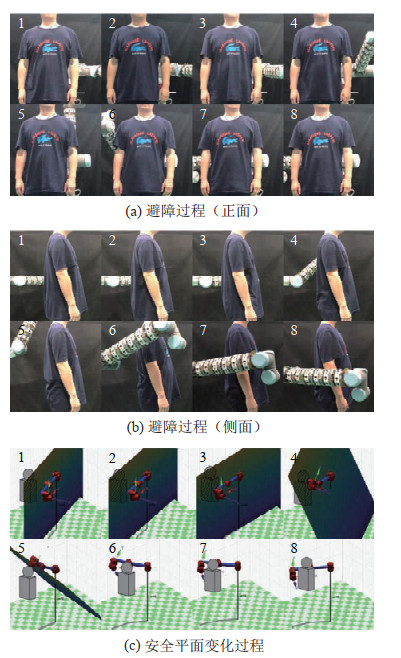
图 19 人体躯干避障实验 Fig.19 The experiment of avoiding human body |

|
图 20 手部干涉避障实验 Fig.20 The experiment of avoiding hand interference |
|
图 21 球体障碍物避障实验数据 Fig.21 The experiment data of avoiding spherical obstacle |
|
图 22 圆柱体障碍物避障实验数据 Fig.22 The experiment data of avoiding cylindrical obstacle |
|
图 23 长方体障碍物避障实验数据 Fig.23 The experiment data of avoiding rectangular obstacle |
|
图 24 背包与圆柱体障碍物避障实验数据 Fig.24 The experiment data of avoiding bag and cylindrical obstacle |
|
图 25 人体躯干避障实验数据 Fig.25 The experiment data of avoiding human body |
|
图 26 手部干涉避障实验数据 Fig.26 The experiment data of avoiding hand interference |
在3种常见形状的障碍物避障实验中,UR10机器人在第3、4阶段通过绕行成功地逃离了局部最优陷阱并且最终在第5~8阶段避开了挡在原路径上的障碍物抵达目标位姿,验证了所提算法的有效性。在进行不规则形状组合障碍物避障实验与人体躯干避障实验时,UR10机器人也成功实现了避障,前者局部最优陷阱发生在第3、4阶段,后者发生在第3、4与第5、6阶段,算法均通过绕行来逃离局部最优陷阱,说明对于多障碍物、障碍物形状不规则以及尺寸较大的情况,该算法同样适用,验证了所提算法的鲁棒性。在手部干涉避障实验中,如图 26(a)所示,UR10机器人的第1、3关节在第2、3、6阶段感应到突然出现的手部肢体时能够及时作出反应,当手部逐渐靠近连杆时,连杆相应地后退以避免碰撞并试图避开,最终在第9~12阶段UR10机器人通过绕行成功地逃离了局部最优陷阱,避开了挡在路径上的手部肢体并抵达目标位姿,这说明应对突然出现的障碍物时,本文算法也可以及时调整避障路径,验证了该算法的实时性。值得注意的是,当算法进入局部最优陷阱并采用绕行方式时,人工势场法的原势能曲线上升,在绕行时势能曲线下降。
然而,实验中传感器会通过串口互相干扰造成随机性的数据异常,这会造成构造出的安全平面发生突变从而导致了图 21 ~图 26中各关节在运行时出现轻微抖动的现象,同时也引起人工势场法势能曲线的波动。
5 结论(Conclusion)本文提出了一种基于接近觉的机械臂避障路径规划方法,将接近觉传感器组成阵列布置在机械臂连杆表面,该方法采用了基于势函数与关节空间的人工势场法,并提出了基于绕行的改进方法以解决传统人工势场法的局部最优问题。最终,在UR10机器人上验证了所提方法的有效性、鲁棒性与实时性。
| [1] |
Zhao X L, Zhang J, Tian J M, et al. Multiscale object detection in high-resolution remote sensing images via rotation invariant deep features driven by channel attention[J]. International Journal of Remote Sensing, 2021, 42(15): 5764-5783. DOI:10.1080/01431161.2021.1931537 |
| [2] |
Giveki D. Robust moving object detection based on fusing Atanassov's intuitionistic 3D fuzzy histon roughness index and texture features[J]. International Journal of Approximate Reasoning, 2021, 135: 1-20. DOI:10.1016/j.ijar.2021.04.007 |
| [3] |
Ren S Q, He K M, Girshick R, et al. Faster R-CNN: Towards real-time object detection with region proposal networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(6): 1137-1149. DOI:10.1109/TPAMI.2016.2577031 |
| [4] |
郭毓, 苏鹏飞, 吴益飞, 等. 基于Faster R-CNN的机器人目标检测及空间定位[J]. 华中科技大学学报(自然科学版), 2018, 46(12): 55-59. Guo Y, Su P F, Wu Y F, et al. Object detection and location of robot based on Faster R-CNN[J]. Journal of Huazhong University of Science and Technology (Natural Science Edition), 2018, 46(12): 55-59. |
| [5] |
杜学丹, 蔡莹皓, 鲁涛, 等. 一种基于深度学习的机械臂抓取方法[J]. 机器人, 2017, 39(6): 820-828, 837. Du X D, Cai Y H, Lu T, et al. A robotic grasping method based on deep learning[J]. Robot, 2017, 39(6): 820-828, 837. DOI:10.13973/j.cnki.robot.2017.0820 |
| [6] |
Chao Y, Chen X C, Xiao N F. Deep learning-based grasp-detection method for a five-fingered industrial robot hand[J]. IET Computer Vision, 2019, 13(1): 61-70. DOI:10.1049/iet-cvi.2018.5002 |
| [7] |
Schwarz M, Milan A, Periyasamy A S, et al. RGB-D object detection and semantic segmentation for autonomous manipulation in clutter[J]. International Journal of Robotics Research, 2017, 37(4-5): 437-451. |
| [8] |
任亚冰. 基于机器学习的机械臂运动规划研究[D]. 成都: 电子科技大学, 2019. Ren Y B. Research on trajectory planning of manipulator based on machine learning[D]. Chengdu: University of Electronic Science and Technology of China, 2019. |
| [9] |
Tsuji S, Kohama T. Proximity and contact sensor for human cooperative robot by combining time-of-flight and self-capacitance sensors[J]. IEEE Sensors Journal, 2020, 20(10): 5519-5526. DOI:10.1109/JSEN.2020.2969653 |
| [10] |
宗成星, 陆亮, 雷新宇, 等. 一种基于A*算法的空间多自由度机械臂路径规划方法[J]. 合肥工业大学学报(自然科学版), 2017, 40(2): 164-168. Zong C X, Lu L, Lei X Y, et al. A path planning approach for multi-DOF spatial manipulator via A* algorithm[J]. Journal of Hefei University of Technology (Natural Science), 2017, 40(2): 164-168. DOI:10.3969/j.issn.1003-5060.2017.02.005 |
| [11] |
王伟, 杨扬, 原魁, 等. 机器人C-空间障碍边界建模与无碰路径规划[J]. 机器人, 1998, 20(4): 280-286. Wang W, Yang Y, Yuan K, et al. Robot C-obstacle boundary modeling and collision-free path planning[J]. Robot, 1998, 20(4): 280-286. DOI:10.3321/j.issn:1002-0446.1998.04.007 |
| [12] |
刘晓磊, 蒋林, 金祖飞, 等. 非结构化环境中基于栅格法环境建模的移动机器人路径规划[J]. 机床与液压, 2016, 44(17): 1-7. Liu X L, Jiang L, Jin Z F, et al. Mobile robot path planning based on environment modeling of grid method in unstructured environment[J]. Machine Tool and Hydraulics, 2016, 44(17): 1-7. |
| [13] |
李洋, 徐达. 基于引力自适应步长RRT的双臂机器人协同路径规划[J]. 机器人, 2020, 42(5): 606-616. Li Y, Xu D. Cooperative path planning of dual-arm robot based on attractive force self-adaptive step size RRT[J]. Robot, 2020, 42(5): 606-616. |
| [14] |
关英姿, 宋春林, 董惠娟. 空间自由漂浮机器人对运动目标抓捕的路径规划[J]. 机器人, 2017, 39(6): 803-811. Guan Y Z, Song C L, Dong H J. Path planning of the free-floating manipulator for capturing a moving target[J]. Robot, 2017, 39(6): 803-811. |
| [15] |
李东方, 李科伟, 邓宏彬, 等. 基于人工势场与IB-LBM的机器蛇水中2D避障控制算法[J]. 机器人, 2018, 40(3): 346-359. Li D F, Li K W, Deng H B, et al. The 2D aquatic obstacle avoidance control algorithm of the snake-like robot based on artificial potential field and IB-LBM[J]. Robot, 2018, 40(3): 346-359. |
| [16] |
李晔, 姜言清, 张国成, 等. 考虑几何约束的AUV回收路径规划[J]. 机器人, 2015, 37(4): 478-485. Li Y, Jiang Y Q, Zhang G C, et al. AUV recovery path planning method considering geometrical constraints[J]. Robot, 2015, 37(4): 478-485. |
| [17] |
Zhang Y T, Zhao G. Research on multi-service demand path planning based on continuous Hopfield neural network[M]// Lecture Notes in Electrical Engineering, Vol. 286. Berlin, Germany: Springer, 2014: 417-430.
|
| [18] |
李娜. 面向人机协作安全保障的工业机器人路径规划研究与实现[D]. 武汉: 武汉理工大学, 2018. Li N. Research and implementation on path planning of industrial robot towards safety assurance of human-robot collaboration[D]. Wuhan: Wuhan University of Technology, 2018. |
| [19] |
汪首坤, 朱磊, 王军政. 基于导航势函数法的六自由度机械臂避障路径规划[J]. 北京理工大学学报, 2015, 35(2): 186-191. Wang S K, Zhu L, Wang J Z. Path plan of 6-DOF robot manipulators in obstacle environment based on navigation potential function[J]. Transactions of Beijing Institute of Technology, 2015, 35(2): 186-191. |
| [20] |
Sang H Q, You Y S, Sun X J, et al. The hybrid path planning algorithm based on improved A* and artificial potential field for unmanned surface vehicle formations[J]. Ocean Engineering, 2021, 223. DOI:10.1016/j.oceaneng.2021.108709 |
| [21] |
宋建辉, 代涛, 刘砚菊, 等. 基于改进人工势场法的移动机器人路径规划[J]. 计算机工程与科学, 2017, 39(7): 1328-1332. Song J H, Dai T, Liu Y J, et al. Path planning of mobile robots based on improved artificial potential field method[J]. Computer Engineering and Science, 2017, 39(7): 1328-1332. |
| [22] |
周自维, 周冰, 赵雪. 基于改进人工势场的多机器人编队控制[J]. 科技创新与应用, 2015(33): 44-45. Zhou Z W, Zhou B, Zhao X. Formation control of multi robots with improved artificial potential field method[J]. Technology Innovation and Application, 2015(33): 44-45. |
 2022, Vol. 44
2022, Vol. 44


