1 引言（Introduction）

冰壶六足机器人是北京2022年冬奥会组委会需求的唯一进入冬奥会赛场的机器人，开发该机器人旨在借助北京冬奥会展示我国机器人的自主创新能力。2021年在科技部科技冬奥专项的支持下，我们充分发挥丰富的想像力和创造力，挑战该项艰巨、紧迫和重大的任务，寻觅和诠释冰壶六足机器人的独特设计创意，即模仿冰壶运动员投掷冰壶的“行为特征”来设计六足冰壶机器人，最终通过冬奥会展示出这些创意。

2018年平昌冬奥会后，国际上开始出现轮式有源驱动冰壶机器人研究文章^[1-2]。轮式冰壶机器人不是直接模仿人击打冰壶的行为，而是利用轮式机器人的车轮与冰面摩擦驱动冰壶的运动。设计出模仿人投掷冰壶行为的六足机器人，是前人尚未系统研究的科学问题，是一个从无到有的研究过程。模仿人投掷冰壶的行为必须突破多任务、多功能、多末端输出的冰壶机器人设计面临的多项挑战，必须攻克机器人的关键基础部件的核心技术，要解决模仿人投掷冰壶行为的六足机器人的构形综合^[3]、投掷冰壶任务链与机器人行为链关联特征建立、机器人击打冰壶行为规划等问题。

2 冰壶六足机器人构形（Configuration of the six-legged curling robot）

在冰壶比赛中人的行为主要有两大功能，即能在冰面上行走和投掷冰壶。行走功能的作用主要是使人在冰面上移动来寻找起滑架等。而投掷冰壶功能的行为复杂，即一条腿支撑身体、另一条腿蹬踏起滑架；一只手握持冰刷接触冰面来平衡身体保持稳定、另一只手握持冰壶手柄来控制冰壶的速度和方向；双目瞄准目标后蹬踏滑行掷出冰壶。

冰壶机器人设计的关键是模仿人投掷冰壶的行为。如图 1所示，机构构形方案采用6条腿，包括2条前腿、2条中腿、2条后腿，再加上一个安装有视觉相机的机械臂。在投掷冰壶过程中，六足机器人前部双腿转化为人手的功能，完成抱壶和旋转壶的运动；中部双腿的膝盖和前部双腿的肘关节复合成四点接触冰面，形成人支撑腿的功能；后部双腿蹬踏起滑架，实现推动机器人加速和滑行的功能；另外，前部双腿在机器人滑行过程中完成二次推壶的任务。投掷冰壶动作结束后，机器人从投掷冰壶的构态转换成站立构态，完成冰面行走和寻找起滑架任务。6条腿分成前、中、后3组，各组具有不同功能和各自异构性，又有相互内在的联系和一致性。

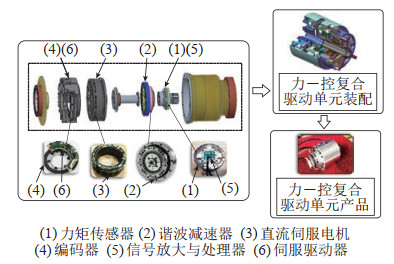
开发冰壶六足机器人关键基础部件的技术瓶颈之一是“力－控”复合驱动单元，如图 2所示。该复合驱动单元是把力矩传感器、谐波减速器、直流伺服电机、编码器、力信号放大处理器、电机伺服驱动器等部件都设计在一个部件中，不仅要求复合驱动单元有一个主轴贯穿其中，结构完整、轻量化、精度合理匹配，而且要非常紧凑。“力－控”复合驱动单元的开发是冰壶六足机器人研制的基础和前提。

3 冰壶六足机器人行为链（Behaviour chain of the six-legged curling robot）

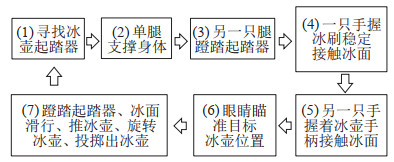
构建冰壶六足机器人行为链，需要研究清楚人投掷冰壶的任务链。图 3所示为人投掷冰壶的任务链，包括7个子任务，即冰面行走寻找起滑架、一条腿支撑身体、另一条腿踏在起滑架上、一只手用冰刷触冰面来辅助支撑身体、另一只手握冰壶手柄接触冰面、双目瞄准目标、蹬踏－滑行－推转冰壶等子任务。

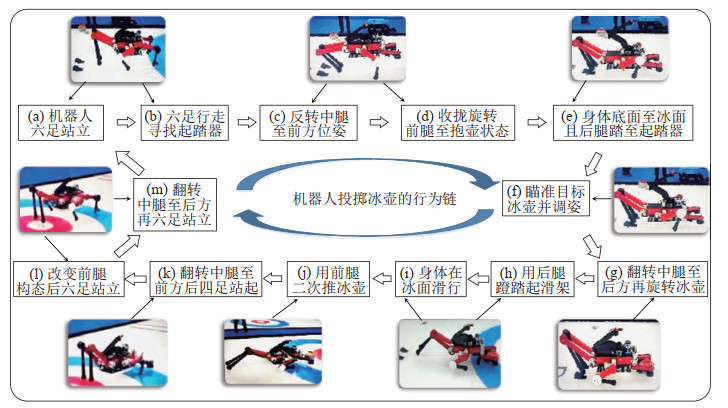
为了模仿人投掷冰壶的行为特征，同时还要体现冰壶六足机器人的特性，设计了冰壶六足机器人的拟人行为链，如图 4所示。冰壶六足机器人处于六足位姿站立于冰面上，通过3-3构态在冰面倒退行走来寻找到起滑架；在前、后4足站立时将2条中腿由后方反转至前方，用中腿和后腿4足站立并将前腿收拢向内旋转至抱壶状态；利用中腿和后腿4足站立将机器人身体底部放置于冰面上，再通过中腿和后腿以及机身底部在冰面上的交替支撑使机器人后腿移至起滑架；在后腿2足踏实起滑架并且2只中足和机身底部接触冰面后抬高相机手臂，利用视觉测量目标冰壶的颜色和位姿坐标，根据测量的目标位姿坐标利用中、后腿4足调整机器人的身体方位；在后腿2足踏实起滑架并且机身底部接触冰面时将2条中腿翻转至后方，然后根据人投壶时旋转冰壶旋向和转速的经验利用前腿旋转冰壶；在中腿2个膝关节和机身底部接触冰面时，按7次多项式和给定的冰壶位置、速度、加速度和加速度导数规划的后腿2足轨迹蹬踏起滑架，驱动身体和冰壶在冰面滑行，再根据7次多项式规划通过前腿二次推冰壶来实现规划要求的速度，完成投掷冰壶过程；翻转中腿至前方后实现中、后腿4足在冰面稳定起身站立；改变前腿构态实现6足站立后，将中腿翻转至后方再保持6足站立和行走。这是所设计规划的冰壶六足机器人拟人投掷冰壶的行为链。

4 冰壶六足机器人投壶轨迹规划（Trajectory planning of curling stone delivery by the six-legged curling robot）

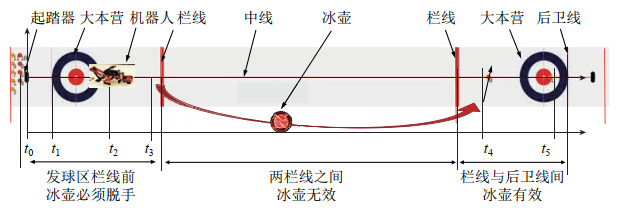
为了更好地实现冰壶六足机器人拟人投掷冰壶的行为链，必须合理规划冰壶六足机器人关键行为子链的运动。图 5所示为机器人投掷冰壶的场地区域的划分。在起滑架至栏线之间机器人必须掷出冰壶，这要求规划好机器人蹬踏起滑架的运动轨迹和冰壶转速以及两前臂二次推壶的运动轨迹；在中间区域，冰壶根据脱离机器人的位置、速度、角速度大小和方向克服冰面摩擦力无动力滑行；在后续区域，投掷的冰壶停至大本营期望的位置或击打指定的冰壶将其撞至希望的位置。在图 6中，当机器人机身底部接触冰面并且后腿2足踏实起滑架时，根据人投壶时旋转冰壶旋向和转速的经验参数，利用前腿旋转冰壶；在中腿2个膝关节和机身底部接触冰面时，按给定冰壶运动参数规划出两后腿足端的7次多项式轨迹，蹬踏起滑架（见图 6(a)），驱动身体和冰壶在冰面滑行（见图 6(b)）；最后按7次多项式规划前腿轨迹，实现二次推冰壶，从而完成冰壶投掷（见图 6(c)）。

如图 6所示，机器人投掷冰壶的过程可以分为两后腿足端蹬踏起滑架推动身体和冰壶运动、冰面滑行、两前腿足端二次推壶3个阶段，而两后腿足端蹬踏起滑架和两前腿足端推壶轨迹都是按7次多项式和给定的冰壶位置、速度、加速度和加速度导数规划的，如式(1) 所示。定义$ q_{j} $为机器人本体与后足或前足端的相对位移，$ t_{0} $、$ t_{1} $、$ t $分别为规划开始、结束和当前时刻，$ q_{0}, q_{1}, v_{0}, v_{1}, a_{0}, a_{1}, j_{0}, j_{1} $分别为冰壶在$ t_{0} $、$ t_{1} $两个时刻的位置、速度、加速度、加加速度。将这些参数代入式(1) 及其关于时间$ t $的1阶、2阶、3阶导数方程，可以建立关于$ c_{i} $（$ i= 0, 1, 2, \cdots, 7 $）的8个方程组，从而可以求出$ c_{i} $，实现3阶导数可控的冰壶驱动运动规划。

$ \begin{align} q_{j} =\, & c_{0} +c_{1} (t-t_{0})+c_{2} (t-t_{0})^{2}+c_{3} (t-t_{0})^{3} + \\ & c_{4} (t-t_{0})^{4}+c_{5} (t-t_{0})^{5}+c_{6} (t-t_{0})^{6} + \\ & c_{7} (t-t_{0})^{7} \end{align} $

(1)

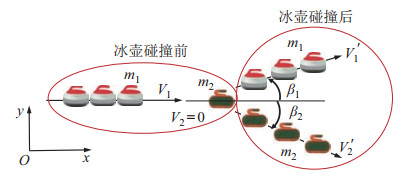
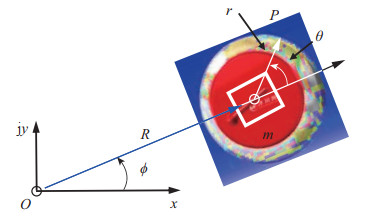
图 7所示为机器人掷壶后冰壶在碰撞前后的运动。利用图 8所示的冰壶运动模型，用一个3自由度的导杆机构来描述冰壶运动，其中导杆$ R $绕坐标原点$ O $转动、滑块在导杆上滑动、冰壶$ r $绕滑块上的铰链转动，这样可以用3自由度的导杆机构替代冰壶来研究其运动。在图 8中，冰壶上任意一点$ P $的位移矢量$ \mathit{\boldsymbol{P}} $、速度矢量$ \dot{\mathit{\boldsymbol{P}}} $、加速度矢量$ \ddot{\mathit{\boldsymbol{P}}} $由式(2)~(5) 以复数向量形式表示，j为复数的虚数单位。

$ \begin{align} \mathit{\boldsymbol{P}} =\mathit{\boldsymbol{R}}+\mathit{\boldsymbol{r}}, \quad \dot{\mathit{\boldsymbol{P}}} =\dot{\mathit{\boldsymbol{R}}}+\dot{\mathit{\boldsymbol{r}}}, \quad \ddot{\mathit{\boldsymbol{P}}} =\ddot{\mathit{\boldsymbol{R}}}+\ddot{\mathit{\boldsymbol{r}}} \end{align} $

(2)

其中

$ \begin{align} \mathit{\boldsymbol{R}} =R{\rm e}^{{\rm j}\phi}, \quad \mathit{\boldsymbol{r}} =r{\rm e}^{{\rm j}(\phi +\theta)} \end{align} $

(3)

这里$ \phi $为$ \mathit{\boldsymbol{R}} $矢量与坐标轴$ x $的夹角，$ \theta $为$ \mathit{\boldsymbol{r}} $矢量与$ \mathit{\boldsymbol{R}} $矢量的夹角。式(3) 两边对时间$ t $求导，可得

$ \begin{equation} \begin{aligned} \dot{\mathit{\boldsymbol{R}}}& =\dot{R}{\rm e}^{{\rm j}\phi} +R\dot{\phi} {\rm e}^{{\rm j} \left(\phi + {\frac{{\rm{ \mathsf{ π} }}} {2}}\right)} \\ \dot{\mathit{\boldsymbol{r}}}& =r({\dot{\phi} +\dot{\theta}}){\rm e}^{{\rm j}\left({\phi +\theta + {\frac{{\rm{ \mathsf{ π} }}} {2}}}\right)} \end{aligned} \end{equation} $

(4)

式(4) 两边对时间$ t $求导，可得

$ \begin{equation} \begin{aligned} \ddot{\mathit{\boldsymbol{R}}}& =\ddot{R}{\rm e}^{{\rm j}\phi} +2\dot{R}\dot{\phi}{\rm e}^{{\rm j} \left(\phi +\frac{{\rm{ \mathsf{ π} }}} {2}\right)}+R\ddot{\phi} {\rm e}^{{\rm j} \left(\phi +\frac{{\rm{ \mathsf{ π} }}} {2}\right)}+R\dot{\phi}^{2}{\rm e}^{{\rm j}(\phi +{\rm{ \mathsf{ π} }})} \\ \ddot{\mathit{\boldsymbol{r}}}& =r({\ddot{\phi} +\ddot{\theta}}){\rm e}^{{\rm j}({\phi +\theta +\frac{{\rm{ \mathsf{ π} }}} {2}})}+r({\dot{\phi} +\dot{\theta}})^{2}{\rm e}^{{\rm j}({\phi +\theta +{\rm{ \mathsf{ π} }}})} \end{aligned} \end{equation} $

(5)

在图 8中，将式(2)(4) 中描述的$ P $点速度分别在$ \mathit{\boldsymbol{R}} $矢量和垂直于$ \mathit{\boldsymbol{R}} $矢量的方向上投影，得式(6) 所示的分速度：

$ \begin{equation} \begin{aligned} v_{P}^{R} & =\dot{R}+r(\dot{\phi} +\dot{\theta})\cos \left({\theta +\frac{{\rm{ \mathsf{ π} }}} {2}}\right) \\ v_{P}^{T} & =R\dot{\phi} +r(\dot{\phi} +\dot{\theta})\sin \left({\theta +\frac{{\rm{ \mathsf{ π} }}} {2}}\right) \end{aligned} \end{equation} $

(6)

式(7) 定义角$ \lambda $：

$ \begin{align} \tan \lambda =\frac{v_{P}^{T}} {v_{P}^{R}} \end{align} $

(7)

因为冰壶所受的冰面摩擦力与式(6)(7) 的速度方向相反，因此可以建立：

$ \begin{equation} \begin{aligned} F_{\rm f} & =\sqrt{ \left({F_{\rm f}^{T}}\right)^{2}+ \left({F_{\rm f}^{R}}\right)^{2}} =mgf\\ F_{\rm f}^{R} & =F_{\rm f} \cos \lambda \\ F_{\rm f}^{T} & =F_{\rm f} \sin \lambda \end{aligned} \end{equation} $

(8)

其中$ m $、$ g $和$ f $分别表示冰壶质量、重力加速度和冰壶与冰面之间的摩擦系数，$ F_{\rm f} $、$ F_{\rm f}^{R} $、$ F_{\rm f}^{T} $分别表示冰壶所受的总摩擦力、沿$ \mathit{\boldsymbol{R}} $矢量方向上的摩擦力分量和垂直于$ \mathit{\boldsymbol{R}} $矢量的方向上的摩擦力分量。

当冰壶转角$ \theta $分别取0和$ {\rm{ \mathsf{ π} }} $时，由式(6)(7) 得角$ \lambda $如下：

$ \begin{equation} \begin{aligned} \tan \lambda_{1} & =\frac{R\dot{\phi} +r({\dot{\phi}+\dot{\theta}})}{\dot{R}}, \; \; \theta =0 \\ \tan \lambda_{2} & =\frac{R\dot{\phi} -r({\dot{\phi}+\dot{\theta}})}{\dot{R}}, \; \; \theta ={\rm{ \mathsf{ π} }} \end{aligned} \end{equation} $

(9)

当冰壶转角$ \theta $分别取0和$ {\rm{ \mathsf{ π} }} $时，因为冰壶前后两部分与冰面摩擦系数不相等，故分别设冰壶前半部分与冰面摩擦系数为$ f_{1} $、冰壶后半部分与冰面摩擦系数为$ f_{2} $，通常$ f_{2} =\eta f_{1} $，其中$ \eta $为2个摩擦系数之间的倍数，得摩擦力如下：

$ \begin{align} F_{{\rm f}_{1}} =\frac{1}{2}mgf_{1}, \quad F_{{\rm f}_{2}} =\frac{1}{2}mgf_{2} \end{align} $

(10)

其中$ F_{{\rm f}_{1}} $和$ F_{{\rm f}_{2}} $分别为冰壶前半部分和后半部分与冰面之间的摩擦力。将式(10) 所描述的摩擦力分别在$ \mathit{\boldsymbol{R}} $矢量方向上和垂直于$ \mathit{\boldsymbol{R}} $矢量的方向上投影，得

$ \begin{equation} \begin{aligned} F_{{\rm f}_{1}}^{T} & =F_{{\rm f}_{1}} \cos \lambda_{1} , \quad F_{{\rm f}_{1}}^{R} =F_{{\rm f}_{1}} \sin \lambda_{1} \\ F_{{\rm f}_{2}}^{T} & =F_{{\rm f}_{2}} \cos \lambda_{2} , \quad F_{{\rm f}_{2}}^{R} =F_{{\rm f}_{2}} \sin \lambda_{2} \end{aligned} \end{equation} $

(11)

由以上各式可以建立冰壶运动动力学方程：

$ \begin{equation} \begin{aligned} I_{A} \ddot{\theta} & =-({F_{{\rm f}_{2}}^{T} +F_{{\rm f}_{1}}^{T}}) r \\ ma^{T}& =F_{{\rm f}_{2}}^{T} -F_{{\rm f}_{1}}^{T} \\ ma^{R}& =-F_{{\rm f}_{2}}^{R} -F_{{\rm f}_{1}}^{R} \end{aligned} \end{equation} $

(12)

其中$ a^{R} $和$ a^{T} $分别为在$ \mathit{\boldsymbol{R}} $矢量方向上和垂直于$ \mathit{\boldsymbol{R}} $矢量的方法上的加速度，$ \ddot{\theta} $为冰壶绕质心$ A $的角加速度，$ I_{A} $为冰壶绕质心$ A $的转动惯量。

由图 7可知，根据机器人掷壶后冰壶在碰撞前后的运动位置和速度要求，先利用式(12) 求解出机器人掷壶要求达到的冰壶运动位置和速度以及转速的大小与方向，再通过图 6和式(1) 求解出在机器人投掷冰壶过程中两后腿足端蹬踏起滑架推动身体和冰壶运动、冰面滑行、两前腿足端二次推壶3个阶段的运动参数，完成冰壶位置、速度、加速度和加速度导数的规划。图 9为冰壶六足机器人在北京冬奥会冰立方冰壶馆的掷壶表演。

5 后记（Postscript）

当进入北京冬奥会冰立方冰壶馆后，在2月16日午夜确定18日中午冰壶六足机器人在冰壶馆赛场公开面对全世界媒体表演，我们只有2个晚上后半夜可以在冰立方冰壶赛场投壶练习，共试投冰壶13次，全部击中目标冰壶，为我们18日中午的机器人公开表演增强了自信心。在2月18日中午的冰壶六足机器人公开表演中，机器人投壶6次，六击六中，圆满完成了北京冬奥会之旅。

开发冰壶六足机器人有3个惊人的地方：(1) 从立项到完成的时间短，冰壶六足机器人是2021年9月9日科技部正式批准立项，2022年2月18日完成表演；(2) 国际上首次成功开发出模仿人投掷冰壶行为的冰壶六足机器人；(3) 北京冬奥会冰立方冰壶馆击打冰壶表演，出现令人出乎意料的精准。对于这段冬奥之旅，我们给出的关键词是“难忘”，冰壶六足机器人的研究充满了许多难忘之事，是我们一生都不会厌倦的研究方向，希望能够一直研究下去，当然还有滑雪、滑冰机器人，但开发冰壶六足机器人是我们的最爱和高光时刻^[4]。在未来，我们将把更多的人工智能技术融入冰壶六足机器人的感知、规划和决策系统，开展冰壶六足机器人之间以及与人之间的冰壶比赛。