碳纤维树脂基复合材料以其优异的力学性能被广泛应用于航空航天、汽车船舶、体育医疗等领域。其中碳纤维树脂基复合材料织物预浸料(下文简称织物)除了具有重量轻、强度高、抗冲击性能好、损伤容限高等优异的力学性能外[1],其经纬线绕交点旋转产生的面内剪切变形使其能够克服双曲率曲面的不可展特性,从而能够铺覆于双曲率曲面上,织物与单向预浸带和预浸丝相比可操作性更强,更适用于几何形状较复杂的零件[2-3]。
织物铺放技能包括轨迹和压力两方面,双曲率曲面零件对铺放轨迹与作用力的要求高,自动铺带常用的固定角度轨迹不易满足铺放要求,织物力学性能的非线性导致铺放轨迹与作用力难以通过计算获取,因此有必要完整、精确地提取人工铺放技能。对于织物铺放的研究,主要包括对手工铺放动作的分析以及自动铺放的轨迹规划与实现两个方面。Ward团队[4-7]研究了织物铺放时的变形大小、变形顺序与对应的铺放动作间的关系,并通过图像采集铺放动作,指导经验不足的初学者铺放,但给出的操作说明除起始铺放点与铺放方向外很少提供其他信息,不明确的动作定义使工人们的操作存在差异,进而影响铺放效率与质量均一性。在此基础上,Malhan团队[8-9]开发了一套铺放单元,由模具CAD(计算机辅助设计)模型、材料物理模型、路径起止点、抓取点等信息生成机械臂在曲面上的测地线运动轨迹,然后根据经验指定不同区域的铺放压力,在导纳控制框架下初步实现了织物自动铺放。上述研究中,基于轨迹起止点生成测地线轨迹[9]和直接指定零件各个区域铺放压力[8]的技能描述方式不能准确描述铺放技能,基于模仿学习的方法能够更好地解决此问题。
机器人运动技能的模仿学习,是指机器人从示教样本中获得运动技能的一类算法,包括基于单个或少量示教轨迹的运动特征提取与泛化。模仿学习的基本问题包括学习对象的选择、多轨迹概率特征的描述等[10]。织物铺放场景中,铺放轨迹与压力为学习对象。针对力相关技能,Gao[11]提出了同时记录示教运动与力信息然后将其编码为时间无关的概率模型的模仿学习框架,并针对打磨与轴孔装配2个场景开展试验,在力/ 位混合控制框架下采用PI(比例-积分)控制器完成打磨力的跟踪。文[12-13]针对接触任务的模仿学习提出对作用力与轨迹分别建模,然后采用力/ 位混合控制器使接触力满足使用要求,并分别针对装配任务和桌面清理任务开展试验。织物铺放与打磨和桌面清理同属于接触任务,本文将在此基础上针对织物铺放场景完善示教数据采集的细节。
采集的示教数据存在分散性,多次示教数据虽然都是可行的,但依然存在差异且不易筛选,为了降低分散性对重现效果的影响,需要提取其概率特征。周欣宇[14]采用GMM模型示教轨迹建模,再由GMR法给出预测轨迹的条件概率分布,所得的轨迹模型表征效果较好,轨迹可靠性强。文[10]也指出GMM能够有效地学习多训练样本的概率特征,因此,本文也采用GMM建立轨迹与压力的技能模型,再用GMR法得到预测的轨迹与压力,最后使用机械臂结合适当的控制器完成技能的重现。
技能重现包括位置与力的重现。机械臂的位置跟踪精度可满足要求,但由GMR法得到的末端执行器轨迹与模具实际位置存在距离,当末端执行器处于此位置时,产生的压力通常不等于GMR法所得压力,不能满足织物铺放对压力的要求,需自行设计力控制器。接触力控制可以分为接触/ 非接触的状态切换与切换后的力跟踪两方面。李琳[15]提出了基于自适应迭代的机器人曲面恒力跟踪算法,轨迹后半段接触力误差小于3 N,但在接触状态切换时存在8 N左右的力冲击。高培阳[16]采用阻抗控制器完成工件打磨场景下的法向力跟踪,根据自抗扰控制原理针对接触状态切换安排过渡过程,虽然可以完成柔顺切换,但是控制器结构较为复杂。当离线规划轨迹与零件实际位置之间的偏差较大时,力控制器的跟踪效果会更难保证。大型风电叶片存在制造误差大、刚度低的特点,连学军[17]采用模糊变阻抗控制策略减小环境与机器人之间的冲击,与未采用阻抗控制的情形相比最大冲击由480 N降低为250 N,2次振荡后达到60 N左右,控制效果还可以进一步提高。Wang[13]在桌面清理任务中使用力/ 位混合控制来调节接触力,接触对象为平面,场景简单,且未给出接触力的具体数值。
综上,针对织物的机器人铺放,现有研究对织物铺放技能的描述不够全面、准确,接触状态切换所用控制器结构较复杂。为此,本文提出织物铺放的轨迹-压力两次示教方法来采集人工铺放技能,并采用GMM法建立技能模型,用GMR法得到预测的轨迹与压力;提出了预控制量退出机制,以便在建立接触状态时完成控制器的无冲击切换,同时在力/ 位混合控制的框架下采用PI控制器实现铺放过程的压力跟踪。值得指出的是,本文的末端执行器仅负责提供压力,织物的牵拉由人工辅助完成。
2 织物铺放技能的采集与描述(Acquisition and description of woven layup skills)在进行织物铺放时,若末端执行器的压力方向与模具法向有偏差,则织物会发生多余的剪切变形,压力不均匀现象也会加剧,因此需要使铺放压力与模具法向方向一致。人工示教铺放难以保证末端执行器的压力方向与模具曲面法向方向一致,为此,本文提出轨迹-压力两次示教的技能采集与描述方法。如图 1所示,通过第1次示教获得末端执行器的原始位姿,使用GMM/GMR法得到预测的轨迹,然后以模具曲面法向和预测轨迹的

|
图 1 轨迹-压力两次示教方法 Fig.1 Method of twice demonstration of trajectory and force |
通过人工示教采集技能数据,常用的示教方法有视觉捕捉示教与拖动示教等。其中视觉捕捉示教的优点在于灵活、省力,且操作员的操作习惯不会被机械臂影响,但是传感器噪声、光照条件、算法误差、标定误差都会影响原始数据质量,而且需要建立从视觉信息到机械臂位姿的映射关系;拖动示教的优势则在于原始数据质量高,可直接用于学习,无需映射,经过练习后操作员可以排除机械臂对操作效果的影响,因此,本文采用拖动示教的方法获取原始数据。
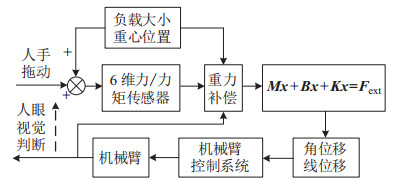
为进行拖动示教,需要机械臂在外力作用下跟随操作员的动作。导纳控制(admittance control),或者说基于位置的阻抗控制,经常应用于机器人与环境或人的交互场景。导纳控制器将外界作用力/ 力矩作为输入,计算出参考运动,使机器人表现出期望的柔顺特性。控制器框架如图 2所示[18],操作员通过视觉判断机械臂的位置来决定人手拖动的作用力,机械臂末端的传感器测得人手拖动力的大小,然后根据负载大小、重心位置和机械臂当前姿态进行末端负载的重力补偿,将补偿后的作用力送入阻抗控制器,计算得到末端执行器的角位移和线位移,再由机械臂控制系统根据这些运动信号控制机械臂的运动。其中导纳控制器的方程如式(1) 所示,
| $ \begin{align} \mathit{\boldsymbol{M}}\ddot{{\mathit{\boldsymbol{x}}}}+{\mathit{\boldsymbol{B}}}\dot{{\mathit{\boldsymbol{x}}}}+\mathit{\boldsymbol{Kx}}=\mathit{\boldsymbol{F}}_{{\rm ext}} \end{align} $ | (1) |
|
图 2 导纳控制框架 Fig.2 Framework of admittance control |
不同于自由空间中的导纳示教仅记录轨迹,接触空间中的示教还要同时记录接触力,单个力/ 力矩传感器不能满足要求,本文采用双传感器串联的方法来解决此问题。如图 3所示,机械臂末端带有一个6维力/ 力矩传感器

|
图 3 双传感器串联布局 Fig.3 Layout of double sensors in series |
由示教轨迹数据学习轨迹技能模型,计算模型输出轨迹的法向姿态,然后使机械臂沿带有法向姿态的轨迹运动,在此轨迹上进行压力示教,获取铺放压力。修改导纳控制器框架为仅保留
通过技能数据分割、法向姿态计算和示教数据概率特征获取,完成铺放技能描述。
2.2.1 技能数据分割采集示教数据后,为了准确高效地从原始数据中截取单条轨迹的示教数据,需要进行自动分割。
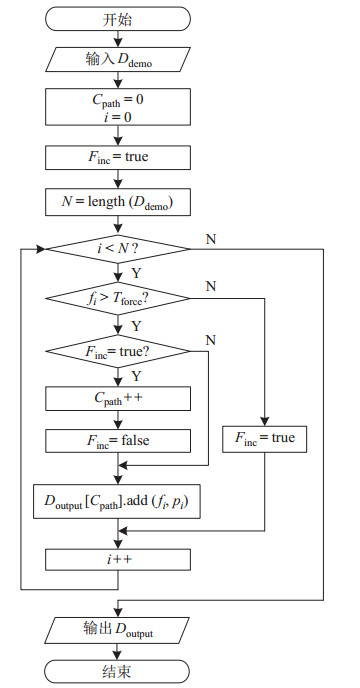
根据示教轨迹分割中先验知识的有无,自动分割方法可分为有监督分割和无监督分割两类[19]。对于织物铺放场景,铺放压力大小可作为分割依据,因此本文采用基于力阈值的有监督轨迹分割。流程如图 4所示,输入示教数据
|
图 4 示教数据分割流程 Fig.4 Segmentation process of the demo data |
示教压力数据按照分割完成后的示教轨迹数据的长度进行分割。
2.2.2 法向姿态计算人工示教不能保证末端执行器的
首先获取曲面上轨迹点所在位置的法向。STL格式文件采用三角片描述几何模型,其中包含曲面离散为三角面片后各三角面片的法向与顶点坐标信息。计算模具曲面STL格式文件中各三角面片形心坐标。再以形心为参考点,找到距离轨迹点最近的三角面片,从STL文件中得到对应位置的法向
然后再以示教姿态的

|
图 5 法向姿态计算 Fig.5 Calculation of the normal orientation |
为降低示教数据分散性对重现效果的影响,需提取其概率特征。采用GMM/GMR法获取示教数据的概率特征,在给定输入条件下得到预测输出。
GMM法使用
| $ \begin{align} P(\mathit{\boldsymbol{x}}_{i} |\mathit{\boldsymbol{\theta}})=\sum _{k=1}^K \alpha_{k} \mathit{\boldsymbol{\phi}} ( \mathit{\boldsymbol{x}}_{i} |\mathit{\boldsymbol{\theta}}_{k}) \end{align} $ | (2) |
式中,
| $ \begin{align} \mathit{\boldsymbol{\phi}} ({ {\mathit{\boldsymbol{x}}}_{i} |{\mathit{\boldsymbol{\theta}}}_{k}})=\frac{1}{({2{{{\rm \mathsf{ π} }}}})^{ \frac{D}{2}}| {{\mathit{\boldsymbol{\varSigma}}}_{k}}|^{ \frac{1}{2}}}{\rm e}^{ \frac{-({{\mathit{\boldsymbol{x}}}_{i} -{\mathit{\boldsymbol{\mu}}}_{k}})^{\rm T}{\mathit{\boldsymbol{\varSigma}}}_{k} ^{-1}({{\mathit{\boldsymbol{x}}}_{i} -{\mathit{\boldsymbol{\mu}}}_{k}})}{2}} \end{align} $ | (3) |
对于高斯混合模型,期望极大化算法(简称EM算法)可以用来迭代计算概率模型的参数[20]。首先需要初始化模型参数,然后逐步进行迭代,EM算法的每次迭代包含2个步骤:E步和M步。
E步,求期望:由当前参数计算第
| $ \begin{align} \gamma_{ik} =\frac{\alpha_{k} \mathit{\boldsymbol{\phi}} ({{\mathit{\boldsymbol{x}}}_{i} |{\mathit{\boldsymbol{\theta}}}_{k}})}{ \sum \limits_{k=1}^K {\alpha_{k} \mathit{\boldsymbol{\phi}} ({{\mathit{\boldsymbol{x}}}_{i} |{\mathit{\boldsymbol{\theta}}}_{k}})}} \end{align} $ | (4) |
M步,求极大:计算下一轮迭代的模型参数:
| $ \begin{align} {\mathit{\boldsymbol{\mu}}}_{k} & = \sum _{i=1}^N {({\gamma_{ik} {\mathit{\boldsymbol{x}}}_{i}})} \bigg/{\sum _{i=1}^N {\gamma_{ik}}} \end{align} $ | (5) |
| $ \begin{align} {\mathit{\boldsymbol{\varSigma}}}_{k} & ={ \sum _{i=1}^N {\gamma_{ik} ({{\mathit{\boldsymbol{x}}}_{i} -{\mathit{\boldsymbol{\mu}}}_{k}})({{\mathit{\boldsymbol{x}}}_{i} -{\mathit{\boldsymbol{\mu}}}_{k}})^{\rm T}}}\bigg/ { \sum _{i=1}^N {\gamma_{ik}}} \end{align} $ | (6) |
| $ \begin{align} \alpha_{k} & =\sum _{i=1}^N \gamma_{ik} \bigg/N \end{align} $ | (7) |
重复进行E步和M步直至收敛,得到高斯混合模型的参数。
数据的拟合效果受到高斯分量个数
| $ \begin{align} {\rm BIC}=-2\ln L+m\ln n \end{align} $ | (8) |
式中,
计算不同高斯分量个数
GMR法常用来从GMM模型中生成回归路径:
| $ \begin{align} P({{\mathit{\boldsymbol{\xi}}}_{t}^{O} |{\mathit{\boldsymbol{\xi}}}_{t}^{I}})\sim \sum _{i=1}^K {h_{i} ({{\mathit{\boldsymbol{\xi}}}_{t}^{I}})} {\rm N}({\hat{\mathit{\boldsymbol{\mu}}}_{i}^{O} ({{\mathit{\boldsymbol{\xi}}}_{t}^{I}}), \hat{\mathit{\boldsymbol{\varSigma}}}_{i}^{O}}) \end{align} $ | (9) |
式中,
| $ \begin{equation} \begin{aligned} & {\mathit{\boldsymbol{\mu}}}_{i} = \begin{bmatrix} {\mathit{\boldsymbol{\mu}}}_{i}^{I} \\ {\mathit{\boldsymbol{\mu}}}_{i}^{O} \end{bmatrix}, \quad {\mathit{\boldsymbol{\varSigma}}}_{i} =\begin{bmatrix} {\mathit{\boldsymbol{\varSigma}}_{i}^{I}} & {\mathit{\boldsymbol{\varSigma}}_{i}^{IO}} \\ {\mathit{\boldsymbol{\varSigma}}_{i}^{OI}} & {\mathit{\boldsymbol{\varSigma}}_{i}^{O}} \end{bmatrix} \\ & \hat{\mathit{\boldsymbol{\mu}}}_{i}^{O} ({{\mathit{\boldsymbol{\xi}}}_{t}^{I}})={\mathit{\boldsymbol{\mu}}}_{i}^{O} +{\mathit{\boldsymbol{\varSigma}}}_{i}^{OI} ({{\mathit{\boldsymbol{\varSigma}}}_{{\mathit{\boldsymbol{i}}}}^{{\mathit{\boldsymbol{I}}}}})^{-1}({{\mathit{\boldsymbol{\xi}}}_{t}^{I} -{\mathit{\boldsymbol{\mu}}}_{i}^{I}}) \\ & \hat{\mathit{\boldsymbol{\varSigma}}}_{i}^{O} ={\mathit{\boldsymbol{\varSigma}}}_{i}^{O} -{\mathit{\boldsymbol{\varSigma}}}_{i}^{OI} ({{\mathit{\boldsymbol{\varSigma}}}_{i}^{I}})^{-1}{\mathit{\boldsymbol{\varSigma}}}_{i}^{IO} \\ & h_{i} ({{\mathit{\boldsymbol{\xi}}}_{t}^{I}})=\frac{{\pi}_{i} {\rm N}({{\mathit{\boldsymbol{\xi}}}_{t}^{I} |{\mathit{\boldsymbol{\mu}}}_{i}^{I}, {\mathit{\boldsymbol{\varSigma}}}_{i}^{I}})}{ \sum\limits _{i=1}^K {{\pi}_{i} {\rm N}({{\mathit{\boldsymbol{\xi}}}_{t}^{I} |{\mathit{\boldsymbol{\mu}}}_{i}^{I}, {\mathit{\boldsymbol{\varSigma}}}_{i}^{I}})}} \end{aligned} \end{equation} $ | (10) |
将示教采集的轨迹与压力按照2维数据处理,以时间为其中一个维度,以轨迹或压力的某一个分量为另一个维度,分别对其建立GMM模型,再用GMR法得到模型预测输出。
3 织物机器人铺放控制(Control of the robotic woven layup)在力/ 位混合控制框架下,采用PID(比例-积分-微分)控制器跟踪参考轨迹与压力。针对接触状态切换过程提出预控制量退出机制,实现无冲击切换。
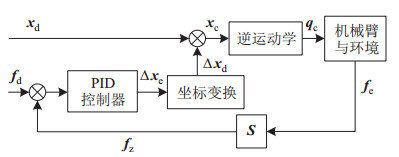
3.1 力/ 位混合控制框架由于不能对一个给定的自由度同时进行力和位置控制,因此必须根据任务场景将位置和力的控制分解到2个正交的子空间[22]。织物铺放场景下,在模具曲面法向采用力控制,其他方向采用位置控制。如图 6所示,其中
|
图 6 力/ 位混合控制框架 Fig.6 Framework of hybrid force/position control |
由GMR法得到的铺放轨迹与模具曲面不重合,轨迹的起始点可能在曲面之上或之下,为了在起始点就能够建立良好接触,需要在执行器从自由空间运动到第1个点的过程中就启动压力控制器。由于使用环境不同,设计2个PID控制器C
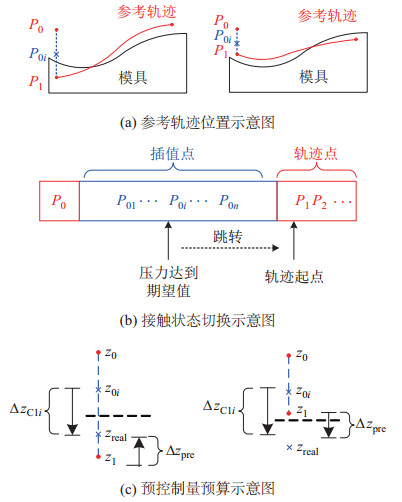
如图 7(a)所示,GMR法输出的某条参考轨迹的起始点
|
图 7 预控制量退出机制 Fig.7 Exit mechanism of the pre-control quantity |
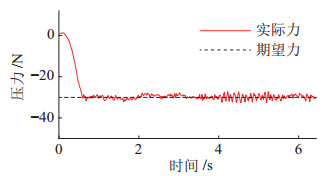
第3条轨迹从模具中心开始,到模具右上角结束,所经过的模具区域曲率大,对力控制器要求高,将其选为试验对象。采集的铺放压力多在20~40 N之间,因此以30 N恒力跟踪为例,采用预控制量退出机制进行接触状态切换。如图 8所示,切换过程中最大压力误差为1.8 N,小于整条轨迹最大误差2.7 N,可认为切换过程无冲击,当不采用此机制而直接进行控制器切换时,末端执行器会承受过大压力导致机械臂停机,无法采集数据,不再给出对比图。
|
图 8 恒力跟踪效果 Fig.8 Result of constant force tracking |
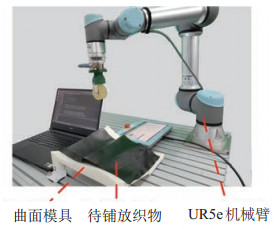
织物铺放试验平台如图 9所示,选择自带6维力/ 力矩传感器的UR5e机械臂,末端安装ATI Gamma六维力/ 力矩传感器,两者性能对比见表 1。末端执行器为聚氨酯压辊,在压力为30 N时,刚度约为18 500 N/m。模具表面为双曲率曲面,采用3D打印制作。织物选用光威复材公司的WP-3021型2/2斜纹织物,厚度约0.25 mm。控制系统基于ROS平台搭建,控制周期设为0.005 s,运行速度约为30~35 mm/s。采用武汉库柏特科技有限公司的COMATRIX-IM 3D视觉平台完成铺放效果评估,其
|
图 9 试验平台 Fig.9 Experiment platform |
|
|
表 1 6维力/ 力矩传感器性能对比 Tab. 1 Performance comparison of six-dimensional force/torque sensors |
对于所用模具,在铺放时织物需要产生一定的面内剪切变形,仅由单台机械臂难以完成曲面铺放,织物定位及牵拉均由人工完成。
进行拖动示教时,要求机械臂随人手施力方向运动,施力一旦消失,机械臂运动立刻停止,因此如式(11) 所示,将阻抗控制方程中的
| $ \begin{align} {\mathit{\boldsymbol{B}}}\dot{{\mathit{\boldsymbol{x}}}}=\mathit{\boldsymbol{F}}_{{\rm ext}} \end{align} $ | (11) |
所用模具每次示教铺放需要约16条轨迹,在易发生褶皱的关键区域由操作员辅助牵拉铺放。重复示教8次,依据第2节相关内容分割示教数据,计算法向姿态,得到参考轨迹。
4.3 轨迹与压力的模型学习由示教数据学习高斯混合模型参数,以第3条轨迹的
| $ \begin{align*} \mathit{\boldsymbol{\mu}}_{1} & =\begin{bmatrix} 0.6125 \\ 0.2888 \end{bmatrix}, \; \; \; \mathit{\boldsymbol{\mu}}_{2} =\begin{bmatrix} 1.7829 \\ 0.3123 \end{bmatrix}, \; \; \; \mathit{\boldsymbol{\mu}}_{3} =\begin{bmatrix} 2.9373 \\ 0.3458 \end{bmatrix} \\ \mathit{\boldsymbol{\mu}}_{4} & =\begin{bmatrix} 4.1108 \\ 0.3813 \end{bmatrix}, \; \; \; \mathit{\boldsymbol{\mu}}_{5} =\begin{bmatrix} 5.2840 \\ 0.4096 \end{bmatrix} \end{align*} $ |
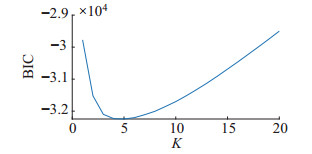
|
图 10 第3条轨迹 |
协方差矩阵为
| $ \begin{align*} \mathit{\boldsymbol{\varSigma}}_{1} & =\begin{bmatrix} 0.1439 & 0.0020 \\ 0.0020 & 0.0001 \end{bmatrix}, \; \; \mathit{\boldsymbol{\varSigma}}_{2} =\begin{bmatrix} 0.1964 & 0.0051 \\ 0.0051 & 0.0002 \end{bmatrix} \\ \mathit{\boldsymbol{\varSigma}}_{3} & =\begin{bmatrix} 0.2048 & 0.0063 \\ 0.0063 & 0.0003 \end{bmatrix}, \; \; \mathit{\boldsymbol{\varSigma}}_{4} =\begin{bmatrix} 0.2097 & 0.0060 \\ 0.0060 & 0.0003 \end{bmatrix} \\ \mathit{\boldsymbol{\varSigma}}_{5} & =\begin{bmatrix} 0.1423 & 0.0027 \\ 0.0027 & 0.0002 \end{bmatrix} \end{align*} $ |
其他维度与轨迹也采用相同做法。获取的GMM模型经过GMR法回归之后得到输出,如图 11所示。由
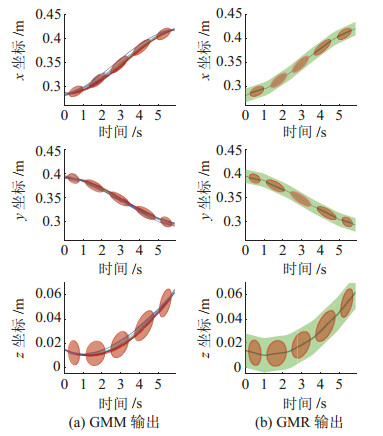
|
图 11 第3条轨迹坐标的GMM与GMR输出 Fig.11 GMM and GMR outputs of the coordinates of the 3rd trajectory |
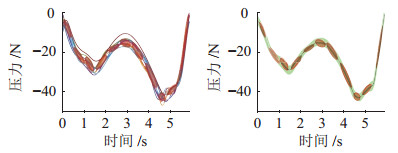
计算得到轨迹法向姿态,在此基础上重新示教获取第3条轨迹
|
图 12 第3条轨迹压力的GMM与GMR输出 Fig.12 GMM and GMR outputs of the contact force of the 3rd trajectory |
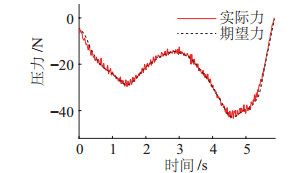
将GMR法给出的参考轨迹与压力发布到机械臂,结合力/ 位混合控制器与接触状态切换的预控制量退出机制完成铺放。在此过程中,考虑到机械臂的运动与发出的控制信号之间存在延迟,在监测到实际压力小于期望压力2~3 N时便开始进行控制器切换。控制器的参数根据聚氨酯压辊刚度选择初值(第3条轨迹比例系数
|
图 13 第3条轨迹的压力 Fig.13 Contact force of the 3rd trajectory |

|
图 14 织物自动铺放效果 Fig.14 Result of automatic woven layup |
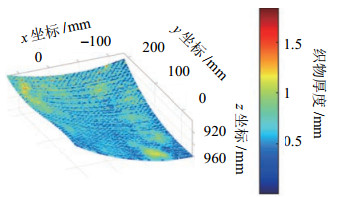
|
图 15 织物厚度 Fig.15 Thickness of the woven |
针对基于模仿学习的双曲率曲面上织物机器人铺放的技能采集、表达与重现展开研究。
1) 提出织物铺放的技能采集、表达方法。通过轨迹-压力两次示教与GMM/GMR法得到铺放轨迹与压力的概率模型,计算得到轨迹点的姿态可保证末端执行器的
2) 针对接触状态切换,提出预控制量退出机制。在接触状态建立过程中计算预控制量,状态切换后使其逐渐衰减,同时压力控制器逐渐接管铺放过程压力控制,使状态切换的压力波动小于2 N。
3) 通过试验验证了提出的双曲率曲面上织物自动铺放的技能采集、表达与重现方法,可完成所设计模具上的织物铺放,铺层贴合良好,无肉眼可见的褶皱、鼓包等缺陷,视觉平台获取的点云显示合格点数量约有97.3%。铺放过程中压力跟踪误差最大为4.0 N,均方根误差为1.1 N。
所设计的曲面模具与实际零件还存在差异,需要织物产生的面内剪切变形程度不同,后续将考虑针对实际零件进行试验,进一步完善本文方法。针对本文的单一零件,GMM/GMR法建立的技能概率模型可以有效地实现技能表达,但是GMM/GMR法存在泛化能力差的缺点,对于相同类型、不同尺寸的其他零件,获取的技能模型难以应用,后续将采用其他模仿学习算法以提高泛化能力。单机械臂难以同时执行抓取与压实操作,本文在试验时由人工辅助沿曲面切向牵拉织物,后续将研究机械臂协作铺放的相关方法。
| [1] |
官威, 李文晓, 戴瑛, 等. 纺织复合材料预制体变形研究综述[J]. 航空制造技术, 2021, 64(Z1): 22-37. Guan W, Li W X, Dai Y, et al. A review of study on deformation of textile composite preforms[J]. Aeronautical Manufacturing Technology, 2021, 64(Z1): 22-37. |
| [2] |
Elkington M, Bloom L D, Ward C, et al. On prepreg properties and manufacturability[C]//19th International Conference on Composite Materials. Montreal, Canada: Concordia Centre for Composites, 2013: 4397-4409.
|
| [3] |
Ward C, Hazra K, Potter K. Development of the manufacture of complex composite panels[J]. International Journal of Materials and Product Technology, 2011, 42(3-4): 131-155. |
| [4] |
Such M, Ward C, Hutabarat W, et al. Intelligent composite layup by the application of low cost tracking and projection technologies[J]. Procedia CIRP, 2014, 25: 122-131. DOI:10.1016/j.procir.2014.10.020 |
| [5] |
Elkington M P, Bloom D, Ward C, et at. Understanding the lamination process[C]//19th International Conference on Composite Materials. Montreal, Canada: Concordia Centre for Composites, 2013: 4385-4396.
|
| [6] |
Prabhu V A, Elkington M, Crowley D, et al. Digitisation of manual composite layup task knowledge using gaming technology[J]. Composites, Part B: Engineering, 2017, 112: 314-326. DOI:10.1016/j.compositesb.2016.12.050 |
| [7] |
Crowley D, Elkington M, Ward C, et al. Hand lay-up of complex geometries-Prediction, capture and feedback[C]//International SAMPE Technical Conference. Diamond Bar, USA: Society for the Advancement of Material and Process Engineering, 2016.
|
| [8] |
Malhan R K, Kabir A M, Shembekar A V, et al. Hybrid cells for multi-layer prepreg composite sheet layup[C]//IEEE 14th International Conference on Automation Science and Engineering. Piscataway, USA: IEEE, 2018: 1466-1472.
|
| [9] |
Malhan R K, Shembekar A V, Kabir A M, et al. Automated planning for robotic layup of composite prepreg[J]. Robotics and Computer-Integrated Manufacturing, 2021, 67. DOI:10.1016/j.rcim.2020.102020 |
| [10] |
黄艳龙, 徐德, 谭民. 机器人运动轨迹的模仿学习综述[J]. 自动化学报, 2022, 48(2): 315-334. Huang Y L, Xu D, Tan M. On imitation learning of robot movement trajectories: A survey[J]. Acta Automatica Sinica, 2022, 48(2): 315-334. |
| [11] |
Gao X, Ling J, Xiao X H, et al. Learning force-relevant skills from human demonstration[J]. Complexity, 2019. DOI:10.1155/2019/5262859 |
| [12] |
Wang Y, Beltran-Hernandez C C, Wan W W, et al. Hybrid trajectory and force learning of complex assembly tasks: A combined learning framework[J]. IEEE Access, 2021, 9: 60175-60186. DOI:10.1109/ACCESS.2021.3073711 |
| [13] |
Wang N, Chen C Z, di Nuovo A. A framework of hybrid force/motion skills learning for robots[J]. IEEE Transactions on Cognitive and Developmental Systems, 2021, 13(1): 162-170. DOI:10.1109/TCDS.2020.2968056 |
| [14] |
周欣宇. 一种基于轨迹模仿学习和任务规划的机械臂演示学习方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019. Zhou X Y. A research on robotic-arm learning method by demonstration based on trajectory imitation learning and task planning[D]. Harbin: Harbin Institute of Technology, 2019. |
| [15] |
李琳, 肖佳栋, 张铁, 等. 基于自适应迭代的机器人曲面恒力跟踪[J]. 北京航空航天大学学报, 2019, 45(4): 641-649. Li L, Xiao J D, Zhang T, et al. Constant-force curved-surfacetracking with robotic manipulator based on adaptive iterative algorithm[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(4): 641-649. |
| [16] |
高培阳. 基于力传感器的工业机器人恒力磨抛系统研究[D]. 武汉: 华中科技大学, 2019. Gao P Y. Research on force control grinding system of industrial robot based on force sensor[D]. Wuhan: Huazhong University of Science and Technology, 2019. |
| [17] |
连学军. 面向大型风电叶片的机器人阻抗控制顺应打磨研究[D]. 武汉: 华中科技大学, 2017. Lian X J. The research of robot adaptable grinding large wind blade by impedance control[D]. Wuhan: Huazhong University of Science and Technology, 2017. |
| [18] |
Yamane K. Admittance control with unknown location of interaction[J]. IEEE Robotics and Automation Letters, 2021, 6(2): 4079-4086. |
| [19] |
迟明善, 姚玉峰, 刘亚欣. 模仿学习示教轨迹自动分割方法的研究进展[J]. 控制与决策, 2019, 34(7): 1345-1354. Chi M S, Yao Y F, Liu Y X. Recent advances on automatic segmentation method of teaching trajectory for imitation learning[J]. Control and Decision, 2019, 34(7): 1345-1354. |
| [20] |
李航. 统计学习方法[M]. 北京: 清华大学出版社, 2012: 162-166. Li H. Statistical learning method[M]. Beijing: Tsinghua University Press, 2012: 162-166. |
| [21] |
Calinon S, Guenter F, Billard A. On learning, representing, and generalizing a task in a humanoid robot[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2007, 32(2): 286-298. |
| [22] |
熊有伦, 李文龙, 陈文斌, 等. 机器人学: 建模、控制与视觉[M]. 武汉: 华中科技大学出版社, 2018: 267-269. Xiong Y L, Chen W L, Chen W B, et al. Robotics: Modeling, control and vision[M]. Wuhan: Huazhong University of Science and Technology Press, 2018: 267-269. |
 2022, Vol. 44
2022, Vol. 44


