2. 天津市智能机器人技术重点实验室, 天津 300350
2. Tianjin Key Laboratory of Intelligent Robotics, Tianjin 300350, China
随着服务机器人越来越多地被部署在医院、商场、展厅等服务场景中,机器人在导航过程中不仅要避让家具等固定障碍物,还要合理避让环境中的人,以保证人的安全性,人机共融成为新一代服务机器人的本质属性[1-2]。在机器人导航中,人的安全包含两个层面的含义:(1) 物理安全:机器人在导航过程中需要与人保持合适的距离防止与人发生碰撞;(2) 心理安全:机器人在导航过程中需要考虑人的心理感受,不能对人造成压力与不适[3]。
在保证物理安全方面,传统的机器人导航算法大多将行人视为与环境中的固定障碍物,然后采用避障算法完成对行人的避让。经典的避障算法,如:DWA(dynamic window approach)[4]、VO(velocity obstacle)[5]、TEB(timed elastic band)[6-7],都能够在人类存在的情况下完成路径规划,但是都没有考虑人的心理感受。
随着近年来服务机器人的广泛使用,一些研究机构以及企业开始在机器人研究中考虑行人的舒适感受,从而使机器人产生更加自然舒适的行为[8-10]。欧盟提出Crowdbot项目[9],计划填补机器人和人类在导航任务中密切互动方面的知识空白。该项目采用了半自动轮椅、Peper人形机器人,以及自主研发的cuyBot机器人3种平台,面向拥挤人群导航、主动提供服务、被人触摸推动等多种服务情景来开发机器人的新能力使其能够安全地以社会可接受的方式在人群中移动。与此同时,不少研究者从空间关系学的理论角度对人的舒适感进行量化建模。Papadakis等[10]根据个人的姿态,如前进方向、面部朝向、手部朝向等因素构造了一个基于偏斜分布密度函数的个人舒适空间。本课题组在这方面也进行了相关研究[11-13],分别采用空间关系学理论构造了基于几何图形的可变舒适空间,利用模糊推理系统构造了基于非对称高斯函数的连续舒适空间。之前的大部分工作都只关注了个人的舒适度,很少对群组的舒适感受进行考虑。生活中的人往往是以群组形式出现的,而本文主要关注的是其中的静态交谈群组。静态交谈群组通常表现出规律的几何构形,先前的研究工作将这些典型的构形统称为F型社交关系[14],常见的F型社交关系构形群组包含如图 1所示的4种,其中2人之间典型的F型社交关系构形群组包括3种:面对面形群组、L形群组和C形群组;3人及以上的人群常构成一个圆形的分布,表示为圆形群组。

|
图 1 典型的F型社交关系构形 Fig.1 Typical F-formation configurations |
关于静态群组的F型社交关系,研究人员从检测到应用都进行了大量的工作。Setti等[15]应用图论方法将空间中的行人作为图的节点,人之间的交互关系作为图的边,然后采用一个图切算法来确定属于同一群组的行人。除此之外,Setti等[16-17]将博弈论、聚类算法、基于投票机制的方法引入到静态交谈群组F型社交关系的检测中。随着深度神经网络的发展,基于深度学习的技术[18]也被引入社交机器人领域中进行行人F型社交关系的识别。
在静态交谈群组F型社交关系的应用方面,研究人员主要研究静态交谈群组的接近[19-21]与避让[22-23]两方面。Yang等[19]提出AppGAN网络用于机器人接近群组,首先合成一个机器人接近群组的数据集,然后使用该数据集训练GAN(generative adversarial network)网络来生成满足人类舒适需求的接近群组轨迹。文[20-21]对比了多种路径生成方法产生的路径的安全性、礼貌性。Sathyamoorthy等[22]构造了一个群组凝聚力方程并将其与基于强化学习的导航系统相结合,实现了机器人对群组的避让行为。
尽管关于机器人如何与群组进行交互的研究已经取得了一定进展,但是对如何定量地评价机器人社交导航的性能仍然有待解决。先前的工作大多采用与人距离的远近[24]、在行人舒适空间停留的时间[25]、基于高斯函数的累积代价值[12]作为评价指标。这些评价指标大多需要预先设置参数,如行人舒适空间的范围、高斯代价函数的幅值以及方差,这些参数在不同的文献中设置并不一致,从而缺乏统一性,并且不能反应人的真实感受。
基于课题组对家庭服务机器人的长期研究工作[11-13],本文利用共同关注区域的概念设计了一个无监督的静态交谈群组检测算法,并应用于实际的机器人导航系统。之后针对社交导航机器人行为难以定量评价的问题,采用图卷积网络搭建了一个评价网络,在公开数据集上的训练结果显示评价网络达到了与人相近的水平。通过将评价网络用于机器人导航行为评估,定量以及可视化定性的结果显示,考虑共同关注区域静态交谈群组的导航系统在导航过程中能够明显提升环境中人类的舒适度。
2 考虑F型社交关系的机器人导航(F-formation aware robot navigation)对与人相关的约束条件进行分析与建模是机器人进行舒适导航的前提。本文面向环境中常见的静态交谈群组,通过分析静态交谈群组常见的空间分布特征,提出基于共同关注区域的群组检测算法,并根据课题组之前的工作[11-12]构造群组舒适空间进而转化成社交代价地图。多层代价地图机制[12]将社交代价地图与机器人进行环境感知获取的环境障碍物地图进行整合,然后作为机器人导航系统的输入,从而实现考虑静态交谈群组的移动机器人舒适导航。
如图 2所示,本文所提的考虑静态交谈群组的移动机器人导航框架包括舒适空间构造、地图表达以及机器人导航3个部分。
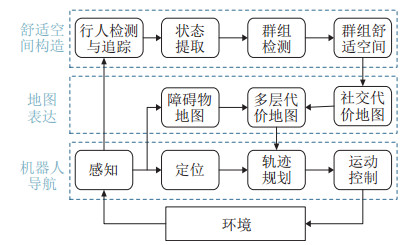
|
图 2 考虑F型社交关系的机器人导航框架 Fig.2 F-formation aware robot navigation framework |
人的检测与追踪是机器人导航的重要组成部分,本文假定机器人可以获取完整的个人状态。在本文中,由于关注的主要是静态交谈的人,所以将行人的状态表示为
| $ \begin{align} h_{i} =\{{x_{i}, y_{i}, \theta_{i}}\} \end{align} $ | (1) |
其中,
| $ \begin{align} f_{i} (x, y)=\;& \exp \{ -[a({x-\tilde{x}_{i}})^{2}-2b({x-\tilde{x}_{i}})({y-\tilde{y}_{i}}) + \\ & c({y-\tilde{y}_{i}})^{2}]\} \end{align} $ | (2) |
其中:
| $ \begin{align} \begin{aligned} a & =\frac{\cos^{2}\theta_{i}} {2\sigma_{x}^{2}} +\frac{\sin^{2}\theta_{i}} {2\sigma_{y}^{2}} \\ b & =\frac{\sin^{2}2\theta_{i}} {4\sigma_{x}^{2}} +\frac{\sin^{2}2\theta_{i}} {4\sigma_{y}^{2}} \\ c & =\frac{\sin^{2}\theta_{i}} {2\sigma_{x}^{2}} +\frac{\cos^{2}\theta_{i}} {2\sigma_{y}^{2}} \end{aligned} \end{align} $ | (3) |
关于静态群组的检测,在机器人领域与计算机视觉领域都进行了大量的研究。但是先前的工作[15-18]大多基于数据驱动,采用机器学习或者深度学习的方式通过大量的数据训练得到。与此不同的是,本文利用之前所提的共同关注区域的概念,通过共同关注区域提取群组中心点进行群组检测。该方法无需数据训练,仅需手动调节少量参数即可完成静态交谈群组的检测。
在获得个人关注区域的表示之后,通过将所有人的关注区域进行叠加可以考虑环境中所有人:
| $ \begin{align} f(x, y)=\sum _i f_{i} (x, y) \end{align} $ | (4) |
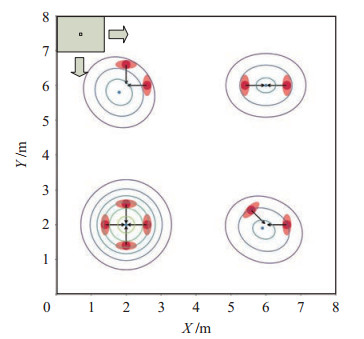
|
图 3 共同关注区域等高线图 Fig.3 The contours of common concern area |
图 3为典型F型社交关系的静态交谈群组共同关注区域的等高线图,其中等高线中心蓝色的点表示群组的中心。在图 3所示的关注区域图上采用左上角的滑动窗口对关注区域图进行遍历,在遍历过程中通过最大值滤波法提取局部最大值,然后将滑动窗口的中心值与滑动窗口范围内的其他区域进行比较,当滑动窗口的中心值比窗口区域内的其他值大时,滑动窗口中心即为群组中心
算法2 静态交谈群组检测算法
输入: 环境中所有人的位置
输出: 群组集合
1: for
2: 初始化一个空群组
3: for
4: 利用式(2) 计算
5: if
6: 将
7: end if
8: end for
9: 将群组
10: end for
11: return
在完成静态交谈群组检测之后,根据文[11-12]构造群组舒适空间。文[11-12]对群组舒适空间进行了描述,群组的舒适空间并不是群组个体舒适空间简单的叠加,群组的成员在维护自身舒适空间的同时也维护着共同关注区域的舒适度,其他人闯入共同关注区域也会引起群组成员的不适。将群组中心视为共同关注区域的中心,并且使用扩展混合高斯模型构造群组舒适空间
| $ \begin{align} F_{{\rm g}_{n}} =\sum _m {w_{m}} f_{{\rm h}_{i}} (x, y)+w_{\rm c} f_{\rm c} (x_{{\rm g}_{n}}, y_{{\rm g}_{n}}) \end{align} $ | (5) |
其中
构造的群组舒适空间并不能直接应用于机器人导航,将环境中所有群组的舒适空间进行累加,然后归一化为0~255的代价地图,同时为了避免机器人与人产生碰撞,在人周围设置了一个禁止通行区域,从而完成社交代价地图的构造。图 4展示了生成的社交代价地图,颜色越接近红色,代表代价值越高,可以看出在群组中心以及人的周围有着较高的代价值。通过ROS(robot operating system)开源导航框架中提供的多层代价地图机制[26-27],可以将社交代价地图与预先建立的环境地图进行叠加并作为轨迹规划模块的输入。

|
图 4 社交代价地图 Fig.4 Social costmap |
机器人导航模块主要包含感知、定位、轨迹规划、运动控制4个部分,本文主要关注的是机器人的轨迹规划部分。文中轨迹规划使用基于时间依赖的A*规划算法[28]。传统的A*规划算法通常在栅格地图也就是2维空间中进行搜索,而时间依赖的A*规划算法将时间信息加入搜索空间。机器人在给定时间内可到达的区域与机器人当前的位姿
| $ \begin{align} U=\{{({e_{x} a_{x}, e_{\phi} a_{\phi}})\mid e_{x}, e_{\phi} \in \{-1, 0, 1\}}\} \end{align} $ | (6) |
其中
| $ \begin{align} \mathcal{C}=\sum _i {w_{i}} \cdot c_{i} \end{align} $ | (7) |
总的代价值
现有用于评价机器人社交导航算法性能的方法多基于机器人与人之间的距离或者其相应的变种[12, 24-25],这种方法具有一定的合理性,但是人的舒适度是主观感受,人舒适感的评估需要人的参与。最近已经有部分工作通过问卷调查采用打分机制来评估机器人行为,通过人在打分过程中的参与来增加评估的真实性。Papenmeier等[29]设计了一个实验来研究机器人的速度大小与朝向对人的影响,实验对仿真机器人设置了多种加减速运动,志愿者首先会观看屏幕上机器人的各种运动,然后通过一个问卷来评估机器人行为给人的感受。实验发现机器人在工作过程中频繁地加减速以及突然的转弯会导致人的不适。Manso等[30]构建了一个用于机器人舒适导航的数据集,首先设计了一个可以随机生成各种机器人与人共存场景的仿真工具[31],然后志愿者会根据机器人在该生成场景中出现的位置给出一个舒适度评分。本文的评价网络就是采用这个开放数据集进行训练的。
3.1 基于图的状态表示图卷积网络[32]成功地将卷积操作应用到了图结构的数据上,并且能够通过修改邻接矩阵来改变节点之间的交互关系。本文将整个场景表示为一个无向图
如图 5所示,机器人节点
| $ \begin{equation} \mathit{\boldsymbol{r}} =[0, 0], \quad \mathit{\boldsymbol{h}} =[x, y, \cos \theta, \sin \theta] \end{equation} $ | (8) |
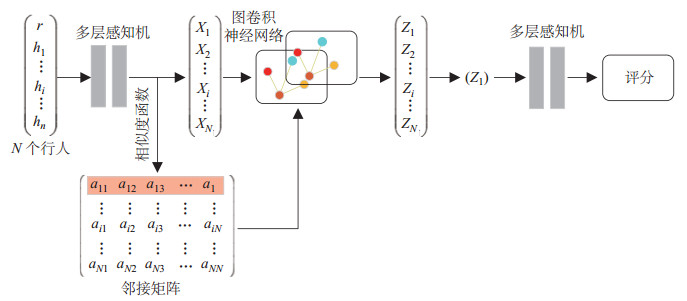
|
图 5 基于图卷积网络的机器人行为评估网络 Fig.5 GCN-based robot behavior evaluation network |
为了进行归一化操作,角度
1) 高斯函数:
| $ \begin{align} f({\mathit{\boldsymbol{x}}_{i}, \mathit{\boldsymbol{x}}_{j}})={\rm e}^{ {\mathit{\boldsymbol{x}}_{i}^{\rm T}}{\mathit{\boldsymbol{x}}_{j}}} \end{align} $ | (9) |
2) 嵌入式高斯函数。高斯函数的一个扩展,可用于计算嵌入空间的相似度:
| $ \begin{align} f({\mathit{\boldsymbol{x}}_{i}, \mathit{\boldsymbol{x}}_{j}})={\rm e}^{\theta ({\mathit{\boldsymbol{x}}_{i}^{\rm T}})\phi ({\mathit{\boldsymbol{x}}_{j}})} \end{align} $ | (10) |
3) 余弦函数。余弦相似度为
| $ \begin{align} f({\mathit{\boldsymbol{x}}_{i}, \mathit{\boldsymbol{x}}_{j}})=\frac{{\mathit{\boldsymbol{x}}_{i}^{\rm T}}{\mathit{\boldsymbol{x}}_{j}}}{|\mathit{\boldsymbol{x}}_{i} ||\mathit{\boldsymbol{x}}_{j} |} \end{align} $ | (11) |
4) 余弦函数+归一化指数函数。在余弦相似度的结果上按行通过softmax函数归一化。
5) 均等注意力函数。所有智能体之间的重要程度相等,即:
| $ \begin{align} f({\mathit{\boldsymbol{x}}_{i}, \mathit{\boldsymbol{x}}_{j}})=\frac{1}{{ {N}}} \end{align} $ | (12) |
其中
| $ \begin{align} {\mathit{\boldsymbol{A}}}={\rm softmax} ({{\mathit{\boldsymbol{XW}}}_{a} {\mathit{\boldsymbol{X}}}^{\rm T}}) \end{align} $ | (13) |
给定特征矩阵
| $ \begin{align} {\mathit{\boldsymbol{H}}}^{(l+1)}=\sigma ({{\mathit{\boldsymbol{AH}}}^{(l)}{\mathit{\boldsymbol{W}}}^{(l)}})+{\mathit{\boldsymbol{H}}}^{(l)} \end{align} $ | (14) |
节点
机器人被固定在第一个节点,通过多层图卷积网络,机器人节点聚合了周围行人节点的信息,机器人节点对应的特征向量为
| $ \begin{align} S=\alpha ({\mathit{\boldsymbol{Z}}}_{1}, {\mathit{\boldsymbol{W}}}_{\alpha}) \end{align} $ | (15) |
其中
实验主要分为2部分,第1部分是评估网络的训练与测试,第2部分是对考虑静态交谈群组的导航系统进行分析。
4.1 评分网络实验 4.1.1 模型设置首先通过一个由多层感知机组成的嵌入层将节点的状态信息映射为32维的特征向量,其中多层感知机的维度为64、32。机器人节点和人类节点输入状态不一致,享有同样的网络架构但是分别定义了2个网络,其中用于人类状态嵌入的网络参数对所有人类节点是共享的。本文设置了3层图卷积网络用于节点间的消息传递,网络层数分别为32、64、32。用于评分的多层感知机网络仅包含1层,但是后面添加了Sigmoid激活函数使得输出小于1。该网络将图卷积网络输出的32维节点特征值映射为1维的评价分数。使用Adam作为优化器,损失函数与评价函数均为MSE(均方差误差函数)。批处理大小被设置为64,训练循环次数为100,学习率为1e
本文在数据集SocNav1[30]上训练了所提的评估模型,这个数据集也是目前所知的唯一一个用于评估机器人行为对人影响的数据集。该数据集搭建了一个仿真环境,通过仿真环境随机生成不同的场景,然后让多个志愿者同时对机器人在当前场景中的位置进行打分,最后选取打分的平均数作为该场景的最终分数。数据集包含的数据类型有:
1) 人:包括行人编号、位置、朝向角。
2) 机器人:由于场景是以机器人为参考坐标系构建的,所有机器人在数据集当中仅表示该场景存在机器人。
3) 房间:一系列顶点,表示房间各个墙壁的起点与终点。
4) 物体:一系列位置方向数据,表示边长为40 cm的家具的位姿。
5) 连接关系:一系列人—物的编号,表示人—人、人—物之间是否存在交互。
6) 分数:当前场景的分数在0~100之间。分数越低表示机器人的行为越使人不适。
数据集分为训练集、验证集、测试集3部分,其中训练集包含8 168个场景,验证集和测试集都包含556个场景。为了对数据进行扩展,对原始的训练集进行翻转,这样数据集中共包含16 336个场景。虽然数据集中已经包含人—物以及人—人之间的交互关系以及周围的环境信息,但是在实际应用中,这些信息都不是可以直接获取的。因此本文仅使用了人的位置信息,而人—人之间的交互信息是通过相似度函数进行估计得到的。所有的训练都在相同的硬件条件下进行的,处理器为英特尔Xeon Gold 6145 CPU@2.00 GHz,显卡为NVIDIA RTX TITAN GPU。
4.1.3 实验结果与分析测试了多个相似度函数在数据集上的训练效果。从表 1的数据可以看出,使用相似度函数来提取节点之间的关系可以有效地降低训练集的均方误差。而将环境中的所有个体设置为同等重要,训练产生的误差远高于使用相似度函数训练的网络。在所有相似度函数当中,使用嵌入式高斯相似度函数在训练集、测试集上取得的结果是最好的,在训练集上的均方误差为0.0180,在测试集上均方误差为0.0219。为了减小因个人因素产生的误差,SocNav1数据集使用了多个人对所有场景进行标注,最后统计发现不同人标注的平均均方误差为0.022。与表 1中的数据对比可以发现,相比于其他的相似度函数,在仅利用人与机器人的相对位置的情况下,使用嵌入式高斯函数可以获得与人类评分近似的结果。
|
|
表 1 不同相似度函数的训练结果 Tab. 1 The training results based on different similarity functions |
为了进一步验证评估网络的合理性,计算了机器人在不同场景下的评分,并使用热图进行可视化分析。在图 6和图 7中,采用内圈为深红色圆形、外圈为浅红色椭圆的结合体表示人,其中箭头表示人的朝向。对应的热图中,颜色越深代表给人造成的不适感越强。图 6(a)展示了单个人场景中机器人在各个位置出现时给人造成的不适感,可以看出距离人越近给人造成的不适感越强,与此同时在人前方区域的颜色较深,这表示机器人出现在人前方时给人造成的不适感会比后方强,这与人的常识相符合。图 6(b)展示了随机多人交互场景下的机器人出现在各处的不适感热图,可以发现最右方的单个人展示出与图 6(a)相似的热图形状。同时可视化结果显示,机器人距离交互的人群越近,给人造成的不适感越强。图 7展示了机器人在具有典型F型社交关系的场景下各处出现的不适感热图,从图中可以看出机器人在群组的中心处都会造成较强的不适感,这与本文前面所描述的群组舒适空间也是相一致的。
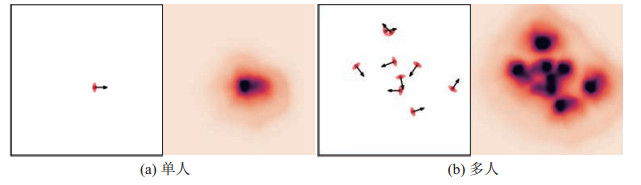
|
图 6 机器人在给定场景下的不适感评分热图 Fig.6 Heatmap of discomfort score for robot in the environment |
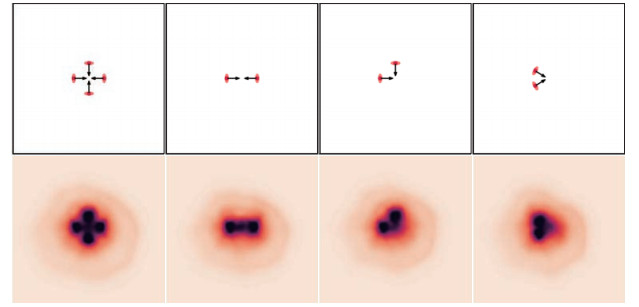
|
图 7 具有F型社交关系构形的群组的不适感评分热图 Fig.7 Heatmap of discomfort score for group with F-formation configuration |
为验证群组检测以及群组舒适空间在导航过程中的有效性,在多个场景下进行导航实验,并利用前面训练的评估网络对机器人行为进行定量评估,同时通过可视化机器人轨迹进行了定性分析。
4.2.1 仿真环境为了实现实验的可重复性,采用3维仿真平台Gazebo搭建了仿真环境,并建立了分辨率为0.1 m的栅格地图用于导航实验。仿真环境与课题组实验室的真实场景相似,大小接近
导航算法的参数设置见表 2,其中静态代价、社交代价的取值范围是ROS导航库中Costmap模块默认的0 ~255,这里设置的是其对应的权重。
|
|
表 2 代价函数权重 Tab. 2 The weights of cost function |
在保持机器人起点、终点以及人的方向距离等参数相同的情况下,设置了多组对比实验来验证群组感知模块的必要性与有效性。图 8(a)展示了对应的导航环境地图,图 8(b)展示了在有无群组感知模块条件下的机器人导航路径对比图,蓝色表示不存在群组感知模块时机器人的运动轨迹,红色表示存在群组感知模块条件下的机器人运动轨迹,轨迹颜色越深代表离目的地越近。图 8(c)(d)分别显示了由评价网络计算的机器人在运行过程中在各个路径点的舒适度。
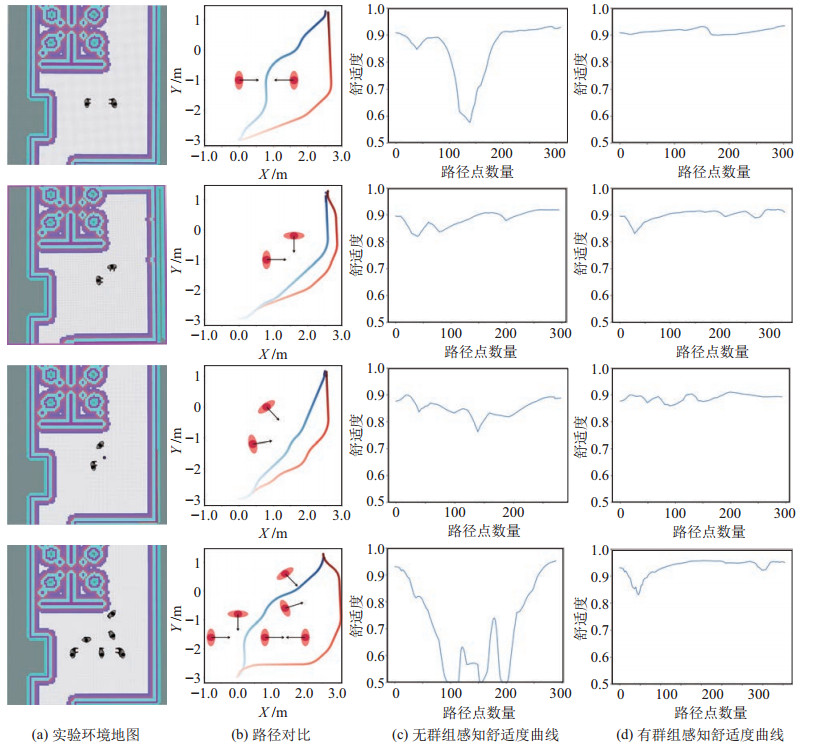
|
图 8 导航实验结果 Fig.8 Results of navigation experiments |
图 8从上到下分别显示了面对面形群组、L形群组、C形群组以及多个群组分布存在下的实验示意图。第1行展示了存在面对面形群组的情况下机器人的导航,可以看出在不存在群组感知模块的情况下,机器人会从正在交谈的2个人中间穿越,显然这种行为会打扰到正在交谈的2人,给他们造成不适感。从第1行对应的舒适度指标图中也可以看出,在不存在群组感知模块时机器人导航的舒适度会发生一个急剧的下降,而在存在群组感知模块时机器人在导航过程中会保持一个相对高且稳定的舒适度。第2、3行分别展示了L形群组与C形群组,这2种情况下机器人产生的轨迹相似,但是具有群组感知模块的机器人在运行过程中会产生离人相对较远的轨迹,同时由对应的舒适度指标图可以观察到,具有群组感知模块的机器人始终维持了较高的舒适度。第4行展示了在多个群组存在的情况下,拥有群组检测模块的机器人能有效避开群组的共同关注区域。
除了定性分析以外,也定量分析了导航算法的有效性。通过将环境中人的位姿转换到机器人坐标系下作为评价网络的输入,计算了路径的平均舒适度与最低舒适度,分数越高代表导航行为给人的舒适感越强,计算结果如表 3所示。在面对面形群组中,群组感知模块可以显著提高机器人导航的舒适性,同时在L形群组和C形群组中,具有群组感知模块的机器人也能产生相对更加舒适且更加稳定的路径。
|
|
表 3 舒适度指标对比结果 Tab. 3 Comparison results of comfort index |
首先设计了一种基于共同关注区域的静态交谈群组检测算法,并利用群组舒适空间构造了考虑群组舒适度的代价地图,将其应用于机器人导航系统实现了考虑群组舒适度的移动机器人导航。同时,提出了一个基于图卷积的机器人导航舒适性评价网络,并测试了多种相似度函数对场景中交互关系建模的能力,效果最好的相似度函数的建模能力达到了与人相似的水平。本文仅考虑了静态交谈场景,未来将考虑动态群组的检测并将行人轨迹预测应用到服务机器人导航中,提升机器人导航的舒适性。除此之外,关于动态场景下的机器人的行为评价也是一个扩展方向,可以利用长短期记忆网络提取行人的动态信息同时采用监督式学习的方式对场景当中智能体之间的交互进行建模。
| [1] |
韩建达, 方勇纯, 赵新, 等. 机器人的智能发育[J]. 人工智能, 2018(3): 28-35. Han J D, Fang Y C, Zhao X, et al. Intelligent development of robots[J]. AI-View, 2018(3): 28-35. |
| [2] |
何玉庆, 赵忆文, 韩建达, 等. 与人共融——机器人技术发展的新趋势[J]. 机器人产业, 2015(5): 74-80. He Y Q, Zhao Y W, Han J D, et al. Tri-Co robot-The new trend in the development of robotics[J]. Robot Industry, 2015(5): 74-80. |
| [3] |
Truong X T, Ngo T D. Dynamic social zone based mobile robot navigation for human comfortable safety in social environments[J]. International Journal of Social Robotics, 2016, 8: 663-684. DOI:10.1007/s12369-016-0352-0 |
| [4] |
Fox D, Burgard W, Thrun S. The dynamic window approach to collision avoidance[J]. IEEE Robotics & Automation Magazine, 1997, 4(1): 23-33. |
| [5] |
Snape J, van den Berg J, Guy S J, et al. The hybrid reciprocal velocity obstacle[J]. IEEE Transactions on Robotics, 2011, 27(4): 696-706. DOI:10.1109/TRO.2011.2120810 |
| [6] |
Roesmann C, Feiten W, Woesch T, et al. Trajectory modification considering dynamic constraints of autonomous robots[C]//7th German Conference on Robotics. Munich, Germany: VDE, 2012: 1-6.
|
| [7] |
Rosmann C, Feiten W, Wosch T, et al. Efficient trajectory optimization using a sparse model[C]//European Conference on Mobile Robots. Piscataway, USA: IEEE, 2013: 138-143.
|
| [8] |
Foster M E, Alami R, Gestranius O, et al. The MuMMER project: Engaging human-robot interaction in real world public spaces[M]//Lecture Notes in Computer Science, Vol. 9979. Berlin, Germany: Springer, 2016: 753-763.
|
| [9] |
Lead T, Lead W P. Safe robot navigation in dense crowds[R/OL]. (2020-05-26)[2021-04-25]. https://cordis.europa.eu/project/id/779942/reporting.
|
| [10] |
Papadakis P, Rives P, Spalanzani A. Adaptive spacing in humanrobot interactions[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2014: 2627-2632.
|
| [11] |
张森, 刘景泰. 基于多维度服务情景的人的舒适需求建模[J]. 机器人, 2019, 41(4): 493-506. Zhang S, Liu J T. Modeling of human's comfort needs based on multi-dimensional service situations[J]. Robot, 2019, 41(4): 493-506. |
| [12] |
周磊, 张森, 赵英利, 等. 基于非对称高斯函数的个人/群组动态舒适空间建模[J]. 机器人, 2021, 43(3): 257-268. Zhou L, Zhang S, Zhao Y L, et al. Modeling of personal/group dynamic comfort space based on asymmetric Gaussian function[J]. Robot, 2021, 43(3): 257-268. |
| [13] |
张森, 周磊, 刘梦, 等. 一种面向狭小、拥挤情景的服务机器人运动规划方法[J]. 机器人, 2021, 43(3): 269-278. Zhang S, Zhou L, Liu M, et al. A motion planning scheme of service robots for cramped and crowded situations[J]. Robot, 2021, 43(3): 269-278. |
| [14] |
Kendon A. Spatial organization in social encounters: The Fformation system[J]. Man Environment Systems, 1976, 6: 291-296. |
| [15] |
Setti F, Russell C, Bassetti C, et al. F-formation detection: Individuating free-standing conversational groups in images[J]. PLoS ONE, 2015, 10(9). DOI:10.1371/journal.pone.0123783 |
| [16] |
Setti F, Lanz O, Ferrario R, et al. Multi-scale F-formation discovery for group detection[C]//IEEE International Conference on Image Processing. Piscataway, USA: IEEE, 2013: 3547-3551.
|
| [17] |
Setti F, Hung H, Cristani M. Group detection in still images by F-formation modeling: A comparative study[C]//14th International Workshop on Image Analysis for Multimedia Interactive Services. Piscataway, USA: IEEE, 2013. DOI: 10.1109/WIAMIS.2013.6616147.
|
| [18] |
Akbari A, Farsi H, Mohamadzadeh S. Deep neural network with extracted features for social group detection[J]. Journal of Electrical and Computer Engineering Innovations, 2021, 9(1): 47-56. |
| [19] |
Yang F K, Peters C. AppGAN: Generative adversarial networks for generating robot approach behaviors into small groups of people[C]//28th IEEE International Conference on Robot and Human Interactive Communication. Piscataway, USA: IEEE, 2019. DOI: 10.1109/RO-MAN46459.2019.8956425.
|
| [20] |
Yang F K, Yin W J, Bjorkman M, et al. Impact of trajectory generation methods on viewer perception of robot approaching group behaviors[C]//29th IEEE International Conference on Robot and Human Interactive Communication. Piscataway, USA: IEEE, 2020: 509-516.
|
| [21] |
Yang F K, Peters C. App-LSTM: Data-driven generation of socially acceptable trajectories for approaching small groups of agents[C]//7th International Conference on Human-Agent Interaction. New York, USA: ACM, 2019: 144-152.
|
| [22] |
Sathyamoorthy A J, Patel U, Paul M, et al. CoMet: Modeling group cohesion for socially compliant robot navigation in crowded scenes[J]. IEEE Robotics and Automation Letters, 2022, 7(2): 1008-1015. DOI:10.1109/LRA.2021.3135560 |
| [23] |
Katyal K, Gao Y X, Markowitz J, et al. Learning a group-aware policy for robot navigation[DB/OL]. (2020-12-22)[2021-04-26]. https://arxiv.org/abs/2012.12291.
|
| [24] |
Vega A, Manso L J, Macharet D G, et al. Socially aware robot navigation system in human-populated and interactive environments based on an adaptive spatial density function and space affordances[J]. Pattern Recognition Letters, 2019, 118: 72-84. DOI:10.1016/j.patrec.2018.07.015 |
| [25] |
Bera A, Randhavane T, Prinja R, et al. SocioSense: Robot navigation amongst pedestrians with social and psychological constraints[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2017: 7018-7025.
|
| [26] |
Lu D V, Hershberger D, Smart W D. Layered costmaps for context-sensitive navigation[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2014: 709-715.
|
| [27] |
Quigley M, Conley K, Gerkey B, et al. ROS: An open source robot operating system[C]//ICRA Workshop on Open Source Software. Piscataway, USA: IEEE, 2009: 3-32.
|
| [28] |
Kollmitz M, Hsiao K, Gaa J, et al. Time dependent planning on a layered social cost map for human-aware robot navigation[C]//European Conference on Mobile Robots. Piscataway, USA: IEEE, 2015. DOI: 10.1109/ECMR.2015.7324184.
|
| [29] |
Papenmeier F, Uhrig M, Kirsch A. Human understanding of robot motion: The role of velocity and orientation[J]. International Journal of Social Robotics, 2019, 11: 75-88. DOI:10.1007/s12369-018-0493-4 |
| [30] |
Manso L J, Nunez P, Calderita L V, et al. SocNav1:A dataset to benchmark and learn social navigation conventions[J]. Data, 2020, 5(1). DOI:10.3390/data5010007 |
| [31] |
Baghel R, Kapoor A, Bachiller P, et al. A toolkit to generate social navigation datasets[M]//Advances in Intelligent Systems and Computing, Vol. 1285. Berlin, Germany: Springer, 2020: 180-193.
|
| [32] |
Kip T N, Welling M. Semi-supervised classification with graph convolutional networks[DB/OL]. (2018-09-09)[2020-09-30]. https://arxiv.org/abs/1609.02907.
|
 2022, Vol. 44
2022, Vol. 44


