近年来,随着机器人技术的不断发展,工业机器人应用越来越多,同时特种机器人的研发及应用也日趋普遍。如今机器人领域研究热点主要集中在功能应用与智能控制两方面,即如何让机器人满足特定条件的功能需求、如何提高与智能制造技术密切相关的机器人智能化水平。但是对机器人能耗特性的研究还未引起足够重视。续航能力是水下、野外、架空环境等工况下特种机器人的重要指标,在满足其特定功能的前提下,如何降低能耗、延长单次作业时间也日渐被关注。架空环境输电线巡检机器人作为架空线移动机器人的典型实例[1],需多次下线更换电源来补给能量,限制了其实用性能。如何延长挂线作业时间、降低在线越障过程能耗,成为迫切需要解决的问题。目前,在硬件及机械加工装配水平一定的条件下,降低机器人能耗的主要途径为控制优化和结构创新。
控制优化角度,即优化其关节空间运动轨迹来降低机器人的能耗,目前机器人能耗优化主要集中在该方向。如Dalla等[2]提出一种基于遗传优化算法的轨迹规划方法。Yang等[3]针对船舶外壁真空吸盘式爬行机器人的能耗问题,提出一种离心风机输出功率的自动控制方法。Ivoilov等[4]从电机驱动控制角度,提出一种减小电流波纹的方法来降低电机功率损耗及发热。Jiang等[5]针对高压线路减震器更换和排水板巡检作业过程,进行运动控制参数优化及验证。管贻生等[6-7]提出一种双平面控制系统进行双足式架空环境移动机器人的能量最优攀爬轨迹规划。邓宗全等[8]提出一种六足式液压驱动野外移动机器人低能耗轨迹规划控制策略。Xie等[9]给出一种麦克纳姆轮移动机器人运动及动力条件约束下的低能耗轨迹规划方法。Zhu等[10]给出了多足运输机器人奔跑过程的腿部轨迹能耗优化控制方法。
结构创新角度,即从改进机器人机械结构出发,在研发阶段即考虑能耗优化目标,开发出满足运动需求的新型低能耗机器人系统。例如,Lee等[11-12]采用并联冗余驱动方式实现机器人系统节能控制,该方法需要额外增加驱动电机的数量,一定程度上增加了机械系统的复杂程度及控制难度。为减轻机器人本体质量和能耗,日本的Morita等[13]提出一种基于伪平行四边形机构的多自由度重力补偿结构,主要通过带和导轮实现。Ulrich等[14]提出一种基于导轮和拉簧的机器人重力补偿机构。Koser等[15]提出了一种采用凸轮机构来调整操作臂底部关节拉簧平衡力矩的设计方法。Cho等[16]提出一种基于差分锥齿轮系的平衡补偿机构,并应用于半球形工作空间的2自由度机器人。房立金等[17]设计了一种双平行四边形机构串联布置的工业机器人结构,各平行四边形机构采用对角电动推缸驱动,可明显降低同等条件下的机器人驱动功率,并可提高机器人末端刚度。Nakayama等[18]提出一种机械式重力补偿装置,主要由弹簧与柔索实现重力补偿以降低能耗,并用于柔索驱动的人体下肢康复系统。Kim等[19]提出基于双平行四边形机构和弹簧柔索的机器人关节结构,可完全补偿本体重力力矩,搭建了5自由度服务机器人样机,仿真及实验结果均表明该机构可明显降低机器人能耗。
以上研究表明,结构创新设计亦是降低机器人能耗的有效途径,现阶段主要为应用弹簧进行重力补偿,或配合使用平行四边形机构进行设计(传统俯仰关节均为单端支撑结构,不具备支撑端切换的能力)。尤其是采用弹簧进行重力补偿的方法,关节在切换支撑端时等效负载将增大,难以满足在架空线机器人巡检特殊工况下降低能耗的需求。综上,本文由俯仰关节的机构学入手,针对多单元串联式移动机器人提出一种基于平行四边形结构的支撑端可切换俯仰关节,延长了其续航能力。
2 机器人构形及俯仰关节结构(Configuration of the robot and structure of the pitching joint)针对一款具有良好转向重力自平衡能力的三臂四单元的架空线移动机器人结构,如图 1所示,重点分析其俯仰关节的力学及能耗特性,该机器人巡检越障流程及运动学分析见文[20]。

|
图 1 机器人构形及实验样机照片 Fig.1 Configuration of the robot and photo of the experimental prototype |
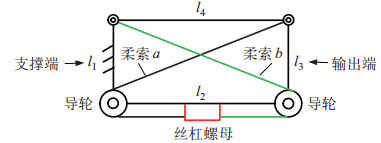
考虑机器人为多单元串联式结构并且存在多单元手臂伸出越障的工况,为简化越障控制算法,基于平行四边形机构设计俯仰单元,即1个俯仰关节等效为1个单元,采用对角柔索驱动方案,如图 2所示。两条柔索分别与机构上端回转轴绑定,分别绕过导轮后与安装于
|
图 2 机器人俯仰单元构形 Fig.2 Configuration of robot pitching unit |
该设计具有如下优点:
(1) 低能耗。①单元机构支撑端竖直时,严格对角驱动的平行四边形机构驱动功率仅与负载重力有关,与负载至关节本体距离无关[17]。②基于图 1中的机器人构形,始终保持手臂竖直,此时水平回转关节能耗可忽略。
(2) 控制简单。支撑端与俯仰运动输出端始终为平行姿态,机器人末端姿态固定,仅解析位置参数即可。
(3) 方向柔性。柔索靠负载或关节自身重力保持拉紧,控制俯仰运动。当手臂进行挂线或抓持运动时,竖直方向具有接触柔性,与环境共融性好。
俯仰关节样机具体结构如图 3所示。机构各杆件

|
图 3 俯仰关节具体结构 Fig.3 Physical structure of the pitching joint |
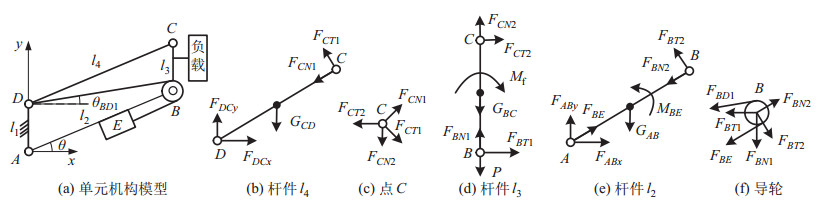
本文所提出机器人俯仰关节由对角柔索驱动,由于驱动柔索要绕过下侧导轮后与丝杠螺母固定连接,为非严格对角驱动,因此需进一步分析其驱动力学特性,建立的关节受力模型如图 4所示。
|
图 4 本文俯仰关节受力模型 Fig.4 Force model of the proposed pitching joint |
由几何关系可以得出:
| $ \begin{align} \theta_{BD{1}} =\;& \arccos {\frac{2l_{BC}^{2} -2l_{BC} l_{AB} \sin \theta} {2l_{BC} \sqrt{l_{BC}^{2} +l_{AB}^{2} -2l_{BC} l_{AB} \sin \theta}}} + \\ & \arcsin \frac{r}{\sqrt{l_{BC}^{2} +l_{AB}^{2} -2l_{BC} l_{AB} \sin \theta}} -\frac{{{\rm \mathsf{ π} }}} {2} \end{align} $ | (1) |
由力学平衡方程可求解出图 4中所示各力,其中电机驱动柔索拉力
| $ \begin{align} F_{BE} =\frac{\cos \theta \left( \frac{G_{AB}} {2}+G_{BC} +P+\frac{G_{DC}} {2}\right)}{ \left({2\sin \frac{\theta -\theta_{BD1}} {2}+ \frac{r}{l_{AB}}} \right)\cos (\theta -\theta_{BD1})} \end{align} $ | (2) |
由式(2) 可以看出,
同时可解出图 4中平行四边形机构4个铰接关节的正交受力,即铰接点
本文俯仰关节驱动电机通过滚珠丝杠拉动柔索控制俯仰角度。可得俯仰关节驱动力矩
| $ \begin{align} T_{\rm s} =\frac{F_{BE} L_{\rm d}} {2{{{\rm \mathsf{ π} }}} \eta_{\rm s}} \end{align} $ | (3) |
其中
传统机器人俯仰关节多采用单杆铰接形式,如图 5所示。其中

|
图 5 传统关节受力模型 Fig.5 Force model of the traditional joint |
可得出该关节的驱动力矩
| $ \begin{align} T_{\rm c} =\frac{G_{T} +2P_{1}} {2}l_{AB} \cos \theta +M_{\rm f1} \end{align} $ | (4) |
同时可得铰接关节正交受力如下:
| $ \begin{align} \begin{cases} F_{Tx} =0 \\ F_{Ty} =G_{T} +P_{\rm l} \end{cases} \end{align} $ | (5) |
驱动负载的运动能耗是机器人俯仰关节能耗的主要方面,其他影响因素还有关节摩擦等。本文机器人俯仰关节由4铰接副组成,传统关节由1铰接副组成,铰接副为关节产生摩擦能耗的主要位置。为准确对比基于2款关节的机器人能耗,下文给出考虑摩擦的关节能耗计算过程。
由式(3)(4) 可直接得出2类机器人俯仰关节负载运动的驱动功率如下:
| $ \begin{align} &\begin{cases} P_{{\rm sy}} =\dfrac{T_{\rm s} n_{\rm s}} {9550} \\[5pt] P_{{\rm cy}} =\dfrac{T_{\rm c} n_{\rm c}} {9550} \end{cases} \end{align} $ | (6) |
| $ \begin{align} &\begin{cases} n_{\rm s} = {\rm d} \Big[\sqrt{l_{\rm s}^{2} -r^{2}}+r \big({{{\rm \mathsf{ π} }}} + \arccos \dfrac{l_{\rm s}^{2} +l_{BC}^{2} -l_{AB}^{2}} {2l_{\rm s} l_{BC}}-\\ \kern 36pt \arccos \dfrac{r}{l_{\rm s}} -\theta\big)\Big]\Big/{{\rm d}\theta} \cdot \dfrac{\omega_{\rm s}} {L_{\rm d}}\\[-2pt] n_{\rm c} =\omega_{\rm c} \end{cases} \end{align} $ | (7) |
其中,
| $ \begin{align} l_{\rm s} =\sqrt{l_{AB}^{2} +l_{BC}^{2} -2l_{AB} l_{BC} \sin \theta} \end{align} $ | (8) |
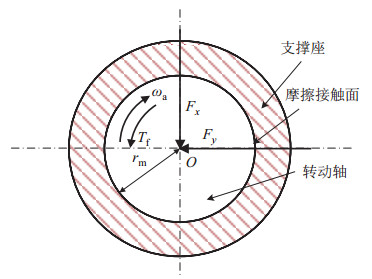
为提高精度,降低磨损,机器人俯仰铰接关节多设计为轴承支撑,其摩擦形式为径向轴颈摩擦,建立摩擦受力模型如图 6所示,其中
|
图 6 径向轴径摩擦受力分析 Fig.6 Radial friction force analysis of the shaft |
可得出摩擦力矩
| $ \begin{align} T_{\rm f} =f_{\rm v} r_{\rm m} \sqrt{F_{x}^{2}+F_{y} ^{2}} \end{align} $ | (9) |
其中,
平行四边形机构俯仰运动时,各铰接关节角速度大小相等,可得出本文俯仰关节运动摩擦总功率
| $ \begin{gather} \begin{cases} P_{{\rm sm}} =\dfrac{T_{{\rm sf}} \omega_{\rm s}} {9550} \\[5pt] P_{{\rm cm}} =\dfrac{T_{{\rm cf}} n_{\rm c}} {9550} \end{cases} \end{gather} $ | (10) |
| $ \begin{gather} \begin{cases} T_{{\rm sf}} = f_{{\rm vs}A} r_{{\rm ms}A} \sqrt{F_{ABx}^{2}+F_{ABy} ^{2}}+\\ \qquad f_{{\rm vs}B} r_{{\rm ms}B} \sqrt{F_{BT1}^{2}+F_{BN1}^{2}} + \\ \qquad f_{{\rm vs}C} r_{{\rm ms}C} \sqrt{F_{CT1}^{2}+F_{CN1}^{2}}+\\ \qquad f_{{\rm vs}D} r_{{\rm ms}D} \sqrt{F_{DCx}^{2}+F_{DCy} ^{2}} \\ {T_{{\rm cf}} =f_{{\rm vc}} r_{{\rm mc}} \sqrt{F_{Tx}^{2}+F_{Ty}^{2}}} \end{cases} \end{gather} $ | (11) |
其中,
最后可得机器人连续工作时间段
| $ \begin{align} \begin{cases} E_{\rm s} =\int _{t_{0}}^{t_{1}} ({P_{{\rm sy}} +P_{{\rm sm}}) {\rm d}t} \\ E_{\rm c} =\int _{t_{0}}^{t_{1}} ({P_{{\rm cy}} +P_{{\rm cm}}) {\rm d}t} \end{cases} \end{align} $ | (12) |
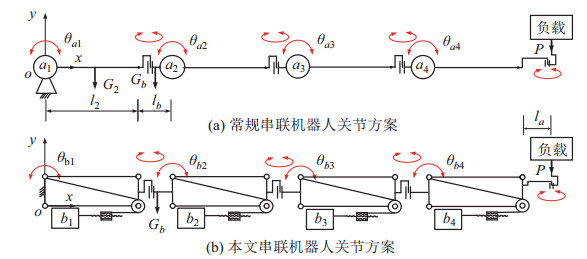
选取一端固定,4俯仰关节和4水平回转关节串联组成的机器人结构方案进行对比,如图 7所示。其中
|
图 7 串联机器人结构对比方案 Fig.7 Comparison of configuration schemes of serial robots |
设铰接关节为跑合状态,取所有当量摩擦系数均为常用的深沟球轴承摩擦系数的上限值,即
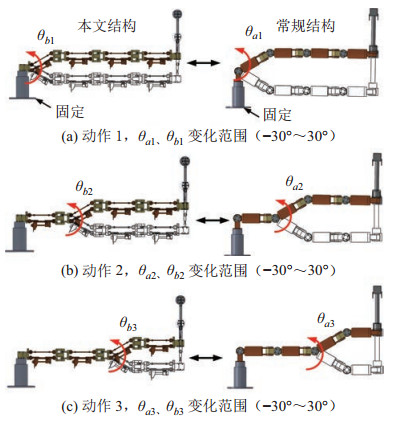
设机器人手臂伸出时只有一个单元做俯仰运动(
|
图 8 串联式结构机器人动作 Fig.8 Actions of the robot with a serial configuration |
由式(12) 可得每个动作下机器人关节驱动负载做俯仰运动时的运动能耗、摩擦能耗、总能耗,如表 1所示,本文关节、传统机器人关节在相同运动条件下各动作的总能耗对比如图 9所示。
|
|
表 1 机器人俯仰运动的运动能耗、摩擦能耗和总能耗 Tab. 1 Motion energy consumption, friction energy consumption and total energy consumption in robot pitching motion |

|
图 9 各动作总能耗对比图 Fig.9 Comparison on the energy consumption of each action |
由表 1及图 9可以看出,各关节驱动能耗由动作1~3依次减小,其原因是动作1~3作用于驱动单元机构上的负载依次减小;在同等运动条件下,本文关节的摩擦能耗大于传统关节,其原因是本文关节的铰接轴较多。但两者的摩擦能耗在总能耗中的占比均极小,为千分比量级,对总能耗影响有限,在工程实际应用中可以忽略;在同等负载条件下,本文关节完成各动作的驱动能耗均小于传统关节,原因是摩擦能耗对机器人关节俯仰运动能耗影响有限,且在不考虑摩擦时,本文关节的驱动转矩与负载等效力矩无关,如式(2) 所示;在完成动作1~3时,本文设计单元结构节省的能耗(
以架空线移动机器人典型越障过程为例进行分析,即中间手臂夹紧输电线路(夹持点可等效为固定端),手臂侧向跨越悬垂绝缘子。对比前侧手臂越障时,新型机器人手臂(装备本文关节)和传统机器人手臂间串联结构的越障能耗特性。下文将本文设计的和传统的两俯仰三水平回转串联结构分别简称为“结构1”“结构2”。结构模型及其D-H坐标系如图 10所示。图中

|
图 10 对比结构模型及D-H坐标系 Fig.10 Comparison of structural model and D-H coordinate system |

|
图 11 对比结构越障动作过程 Fig.11 Obstacle crossing process of the contrastive configurations |
结构1、结构2越障过程中各关节的运动状态分别如表 2、表 3所示。
|
|
表 2 结构1各关节运动状态 Tab. 2 Motion state of each joint in configuration 1 |
|
|
表 3 结构2各关节运动状态 Tab. 3 Motion state of each joint in configuration 2 |
未回转关节可采用机械式自锁,忽略其能耗,绕竖直方向回转关节无俯仰运动,忽略其能耗。在考虑摩擦的情况下,可得出两种对比结构的各俯仰关节的运动能耗,如图 12所示,完成越障过程的总能耗如图 13所示。图 12、图 13中忽略能耗的关节未表示。

|
图 12 考虑摩擦条件下两种对比结构的各关节能耗 Fig.12 Energy consumption of joints in the two contrastive configurations in the case of the friction considered |

|
图 13 两种对比结构的越障总能耗 Fig.13 Total obstacle-crossing energy consumption of the two contrastive configurations |
由图 12可以看出,考虑摩擦条件下,结构1机器人越障时,每一动作的能耗均小于结构2,且完成动作2时,结构1有能耗的关节为2个,结构2有能耗的关节为3个。其原因如下:(1) 当左侧手臂竖直时,本文关节在水平回转时其回转轴始终保持竖直状态,能耗可忽略不计,而结构2的
由图 13可以看出,本文俯仰关节配合水平回转关节串联组成的架空线移动机器人在越障时,其总能耗明显低于相同结构尺寸及质量条件下的、由常规单元机构串联组成的机器人。机器人完成图 11中越障动作可节能约39.4%。
相对于常规机器人单元机构,本文单元可从结构原理上降低机器人能耗,可选取较小型号的驱动电机,减轻机器人质量,提高多单元串联机器人的续航能力。
5 本文俯仰关节样机的能耗实验(Energy consumption experiments on prototype of the proposed pitching joint)采用2个本文俯仰关节串联的结构来验证能耗特性,即俯仰运动驱动能耗与负载等效作用于关节本体的力矩无关。实验样机如图 14(a)所示,俯仰关节1与俯仰关节2由水平回转关节串联连接,采用数显直流电源供电,24 V恒定输出,关节1由电源右侧端子供电,其他电机由左侧端子供电。图中驱动柔索(紧)表示该柔索被拉紧,提供驱动拉力,控制单元的俯仰角度;被动柔索(松)表示该柔索放松悬垂,不提供拉力。后文配图仅用“松”“紧”分别表示驱动柔索和被动柔索。实验用负载如图 14(b)所示,质量为2.8 kg。关节1进行俯仰运动,由

|
图 14 实验样机及负载 Fig.14 Experimental prototype and the load |
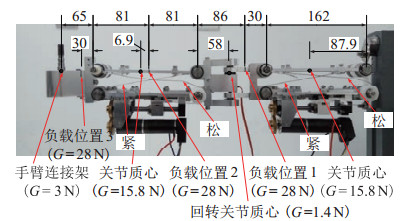
记录负载分别位于图 15中3个不同位置时俯仰运动关节1的电源输出电流。样机尺寸及各关节质心水平初始位置如图 15所示,距离单位为mm。实验过程如图 16所示。俯仰关节1运动过程中驱动电机电流数据如图 17所示。
|
图 15 样机尺寸及负载位置 Fig.15 Prototype size and the load position |

|
图 16 实验过程 Fig.16 Experimental process |
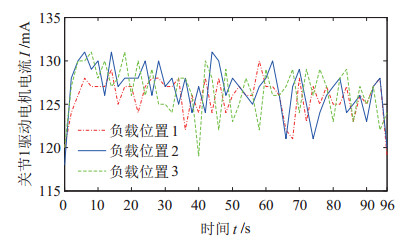
|
图 17 3个负载位置上关节1的驱动电机电流 Fig.17 Current of driving motor in joint 1 in three load positions |
各负载位置1~3所采集电流的平均值分别为125.9163 mA、126.5936 mA、126.5510 mA。
由图 17可以看出,当负载位于3个不同位置时,俯仰关节1驱动电流于115~135 mA区间内波动且无明显大小差别,波动主要位于120~130 mA区间内,各负载位置下电流平均值差小于0.7 mA。位置1的电流平均值略小于位置2和位置3,造成该现象的原因可能是在位置2、3处负载等效作用于关节1的力偶矩较大,导致关节1各回转轴在做俯仰运动时摩擦力较大。电源输出的电压恒为24 V,说明当负载分别位于3个位置时俯仰运动驱动电机的能耗基本一致,未发生改变,这初步验证了本文俯仰关节的驱动力及驱动能耗与负载等效作用于关节的力矩无关的结论。间接证明了基于本文俯仰关节设计的架空线移动机器人或多单元串联式结构的机器人可明显降低能耗。可以选取较小型号的驱动电机,减轻机器人质量,提高续航能力。
6 结论(Conclusion)(1) 提出一种能耗低、控制简单、具有方向柔性的机器人俯仰关节,采用单电机柔索驱动,基于平行四边形结构设计。给出了其典型应用样机基于该关节的多单元串联式架空线移动机器人。
(2) 在考虑摩擦因素的条件下分析关节的受力及能耗特性,结果表明本文关节的驱动柔索拉力仅与负载等效作用于关节本体的重力相关,与等效力矩无关。说明该关节在摩擦系数较小的情况下具有低能耗特性,且负载距关节本体越远,相比于传统俯仰关节的节能效果越明显,尤其适用于多单元串联式悬臂机器人结构。
(3) 考虑摩擦因素,对比分析了基于本文关节和传统俯仰关节的多单元串联结构的俯仰运动、架空线移动机器人的越障运动能耗特性。由于本文关节铰接轴较多,因此其摩擦能耗高于传统关节,但摩擦能耗与运动能耗相比微小。对比之下,本文关节串联结构的俯仰运动能耗明显更低,且负载等效力矩越大,节能效果越好;本文俯仰关节串联组成的架空线移动机器人,手臂越障总能耗明显更低。
(4) 搭建实验样机进行能耗特性验证。结果表明本文关节驱动方案可行;相同负载质量下负载与关节本体距离不同时驱动能耗基本一致。证明了与传统俯仰关节相比其具有低能耗的特性,尤其适用于长悬臂结构。本文可为有节能需求的机器人结构设计提供一定的参考。
| [1] |
Pouliot N, Richard P L, Montambault S. LineScout technology opens the way to robotic inspection and maintenance of highvoltage power lines[J]. IEEE Power and Energy Technology System Journal, 2015, 2(1): 1-11. DOI:10.1109/JPETS.2015.2395388 |
| [2] |
Dalla V K, Pathak P M. Power-optimized motion planning of reconfigured redundant space robot[J]. Journal of System and Control Engineering, 2018, 233(8): 1030-1044. |
| [3] |
Yang Y K, Zhang H, Song Q Z. A study on reducing power consumption of the centrifugal fan for the negative pressure adsorption wall climbing robot[J]. Journal of Physics: Conference Series, 2019. DOI:10.1088/1742-6596/1303/1/012108 |
| [4] |
Ivoilov A, Trubin V, Zhmud V, et al. The power consumption decreasing of the two-wheeled balancing robot[C]//International Multi-Conference on Industrial Engineering and Modern Technologies. Piscataway, USA: IEEE, 2018. DOI: 10.1109/FarEastCon.2018.8602775.
|
| [5] |
Jiang W, Ye G C, Zou D H, et al. Dynamic model based energy consumption optimal motion planning for high-voltage transmission line mobile robot manipulator[J]. Journal of Multi-body Dynamics, 2021, 235(1): 93-105. |
| [6] |
Zhou X F, Jiang L, Guan Y S, et al. Energy-optimal motion planning of a biped pole-climbing robot with kinodynamic constraints[J]. Industrial Robot, 2018, 45(3): 343-353. DOI:10.1108/IR-11-2017-0200 |
| [7] |
江励, 管贻生, 王建生, 等. 爬杆机器人能量最优攀爬运动规划[J]. 机器人, 2017, 39(1): 16-22. Jiang L, Guan Y S, Wang J S, et al. Energy-optimal motion planning for a pole-climbing robot[J]. Robot, 2017, 39(1): 16-22. |
| [8] |
Deng Z Q, Liu Y Q, Ding L, et al. Motion planning and simulation verification of a hydraulic hexapod robot based on reducing energy/flow consumption[J]. Journal of Mechanical Science and Technology, 2015, 29: 4427-4436. DOI:10.1007/s12206-015-0941-0 |
| [9] |
Xie L, Herberger W, Xu W L, et al. Experimental validation of energy consumption model for the four-wheeled omnidirectional Mecanum robots for energy optimal motion control[C]//IEEE 14th International Workshop on Advanced Motion Control. Piscataway, USA: IEEE, 2016: 565-572.
|
| [10] |
Zhu Y G, Guo T. Galloping trajectory generation of a legged transport robot based on energy consumption optimization[J]. Journal of Robotics, 2016. DOI:10.1155/2016/9645730 |
| [11] |
Lee G, Sul S K, Kim J. Energy-saving method of parallel mechanism by redundant actuation[J]. International Journal of Precision Engineering and Manufacturing-Green Technology, 2015, 2: 345-351. DOI:10.1007/s40684-015-0042-7 |
| [12] |
Lee G, Park S, Lee D, et al. Minimizing energy consumption of parallel mechanisms via redundant actuation[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(6): 2805-2812. DOI:10.1109/TMECH.2015.2401606 |
| [13] |
Morita T, Kuribara F, Shiozawa Y, et al. A novel mechanism design for gravity compensation in three dimensional space[C]//IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Piscataway, USA: IEEE, 2003: 163-168.
|
| [14] |
Ulrich N, Kumar V. Passive mechanical gravity compensation for robot manipulator[C]//IEEE International Conference on Robotics and Automation. Piscataway, USA: IEEE, 1991: 1536-1541.
|
| [15] |
Koser K. A cam mechanism for gravity-balancing[J]. Mechanics Research Communications, 2009, 36(4): 523-530. DOI:10.1016/j.mechrescom.2008.12.005 |
| [16] |
Cho C, Lee W, Kang S. Static balancing of a manipulator with hemispherical work space[C]//IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Piscataway, USA: IEEE, 2010: 1269-1274.
|
| [17] |
孙龙飞, 房立金. 机械手臂结构设计与性能分析[J]. 农业机械学报, 2017, 48(9): 402-410. Sun L F, Fang L J. Design and performance analysis of novel robotic arm[J]. Transactions of the Chinese Society of Agricultural Machinery, 2017, 48(9): 402-410. |
| [18] |
Nakayama T, Araki Y, Fujimoto H. A new gravity compensation mechanism for lower limb rehabilitation[C]//International Conference on Mechatronics and Automation. Piscataway, USA: IEEE, 2009: 943-948.
|
| [19] |
Kim H S, Song J B. Multi-DOF counterbalance mechanism for a service robot arm[J]. IEEE/ASME Transactions on Mechatronics, 2014, 19(6): 1756-1763. DOI:10.1109/TMECH.2014.2308312 |
| [20] |
Tao G H, Fang L J. A multi-unit serial inspection robot for power transmission lines[J]. Industrial Robot, 2019, 46(2): 223-234. DOI:10.1108/IR-09-2018-0195 |
 2022, Vol. 44
2022, Vol. 44


