1 引言（Introduction）

定位是移动机器人所必须具备的一项重要功能，是实现地图构建、自主导航等功能的前提和基础^[1]。全球卫星定位系统（GNSS）能够在全球范围内、24小时地提供全局位置信息，是室外车辆所普遍使用的定位技术^[2]。然而，在卫星拒止区域内，例如在室内、地下等，接收器完全接收不到卫星信号时，必须启动备用的导航系统才能完成导航任务^[3-4]。

移动机器人常配备惯性测量单元（IMU）、编码器（encoder）、视觉（vision）传感器和激光雷达（LiDAR）等导航传感器。IMU和编码器虽然成本低廉、原理简单，但定位误差会随时间和运行里程快速累积，通常用于辅助视觉或激光雷达进行定位。视觉定位系统通过对连续的两帧图像进行特征跟踪、特征匹配、位姿递推估计等一系列处理，实现对移动机器人的定位，但在高动态和光照变化明显的情况下，其误差累积会显著增大。

激光定位系统通过点云匹配实现较高精度的位姿估计，具有定位精度高、使用范围广等特点，目前已广泛应用到物流机器人与扫地机器人等低速的移动机器人上^[4]。但是激光定位系统所获得的高精度是以降低输出频率为代价的。LOAM（LiDAR odometry and mapping）^[5]是目前KITTI Odometry数据集^[6]上排名最靠前的定位算法之一，其相对定位误差可达0.55%，输出频率却很低（在NVIDIA Jetson TX2处理器上测试的后端定位频率约1.5 Hz）。为了进一步降低计算量，Shan等^[7]基于特征分割和地面优化技术对LOAM算法进行改进，提出了轻量型的LeGO-LOAM算法，虽然精度和稳定性均有一定的提高，但输出频率仍然偏低（在NVIDIA Jetson TX2处理器上测试的后端定位频率约3 Hz），这对于中、高速移动机器人导航是十分不利的。另外，由于缺乏高度方向上的全局约束，其高度方向上的平均误差约占总体定位误差的70% 以上^[7]。

面对单一传感器的不足，研究人员提出了许多基于多传感器融合技术的组合定位算法。如为了应对光照变化和高速运动时的特征丢失等问题，可将高频率的IMU（惯性测量单元）数据融入到视觉定位系统中，以此来提高系统的鲁棒性和算法的稳定性^[8-9]。其中，Qin等^[9]设计了一个基于优化方法的相机和IMU紧组合定位系统VINS-Fusion，在KITTI Odometry数据集上的测试定位精度为1.09%，是目前较为优秀的双目视觉/惯性融合定位算法。为了弥补激光输出频率低和视觉高动态不稳定的缺点，Zhang等^[10]基于优化融合方法提出了V-LOAM算法，单目视觉模块以60 Hz的频率进行运动估计，激光模块以1 Hz的频率对位姿进行地图匹配优化，实现了0.54% 的定位精度。Kubelka等^[11]认为IMU/编码器/相机/激光雷达组合定位是实现卫星拒止环境下高精度、高可靠性导航的有效方式，并利用EKF算法对IMU/编码器里程计/视觉里程计/激光里程计进行融合，在多种场景下实现了1.2% 的定位精度。但是，这些研究侧重于定位系统的整体设计，编程实现复杂，且导航定位精度往往很难超过在激光雷达可用时的定位精度。

为了避免复杂的系统设计和编程实现，研究人员开始尝试另一条研究思路，即直接对现有的定位系统进行松耦合融合。为此，Moore等^[12]在ROS（robot operating system）环境下设计并实现了一个基于EKF的多传感器融合算法框架robot-localization，可以依照ROS预定义的信息格式，融合任意多个定位子系统的位置、姿态和速度等数据。当前，它已经成为ROS系统上非常流行、被广泛使用的一种定位算法包。但是，该算法在融合定位子系统的位姿时存在着协方差无法确定的问题：在没有卫星定位等全局信息辅助的情况下，激光或视觉定位子系统的位姿输出会随着运动范围的增大而产生误差累积，即位姿估计的不确定度关于时间是无界的^[13]。尽管回环检测能够大幅度减小累积误差，但进行复杂场景下大范围运动时，回环检测常常失效，甚至出现假阳性闭环的问题^[14]。因此，目前还缺少有效方法对激光或视觉定位子系统的协方差进行建模。

另外，在组合定位系统中，速度测量通常是在机器人坐标系中进行（即局部速度测量），而非在世界坐标系中进行（即全局速度测量）。但是，相对于全局速度融合，局部速度融合对于提升系统定位精度的意义并不大。例如IMU/编码器融合定位算法^[15-16]和IMU/相机/编码器融合定位算法^[17]都是先根据正运动学模型和编码器读数计算出局部速度，再将其融入系统的状态中。由于局部速度必须使用最新的姿态估计值将其分解为全局速度才能对位置估计产生约束，因此，这种融合方式对定位结果的影响严重依赖于姿态估计的好坏。如果能够利用IMU和编码器构建一个独立于系统状态的全局速度测量系统，通过卡尔曼观测更新过程直接对系统状态产生约束，便可进一步提升系统的定位精度。

针对定位子系统位姿协方差无法建模和组合定位系统缺少全局速度测量的问题，本文借助当前优秀的激光定位系统和视觉定位系统，设计一个松耦合定位算法IEVL-Fusion，将激光、相机、编码器和IMU快速、高效地集成起来，实现低漂移、高频率的移动机器人定位。首先，考虑到ES-EKF相对于常规的EKF具有一些显著优点^[18-19]：(1) 姿态误差是小量，可用3维向量对其进行等价表示，有利于避免出现协方差奇异问题；(2) 系统误差在0附近，有利于降低系统的非线性程度，提高滤波精度；(3) 系统误差为小量，意味着可忽略二次项及高阶项，使雅可比矩阵的计算变得简单、快速。因此，本文选择ES-EKF作为融合方法。其次，针对激光定位子系统位姿协方差无法建模的问题，将位姿依时间戳转换为位姿增量，并将位姿增量的协方差建模为时间增量的二次函数，建立了位姿增量观测模型。最后，受AHRS可输出全局姿态信息的启发^[20]，利用AHRS输出的全局姿态对正向运动学模型输出的局部速度进行分解，获得对移动机器人全局速度的独立测量结果，从而获得对系统状态的全局速度约束。

本文方法的创新和贡献主要体现在：

(1) 将协方差无法建模的位姿融合问题转化为协方差可建模的位姿增量融合问题，并考虑位姿增量测量输出的不均匀性，将其协方差建模为时间增量的二次函数，有效实现了激光和视觉定位子系统输出的融合；

(2) 设计了一种新型的编码器信息的融合方式，即利用IMU姿态输出和移动机器人正向运动学模型构建全局速度测量子系统，再将全局速度测量值融合到系统状态中，有效降低组合系统的定位误差；

(3) 在街道和野地2个场景中对本文算法进行测试和对比分析，并公开实验中所采集到的数据集，可通过扫码本文标题页的OSID码下载。

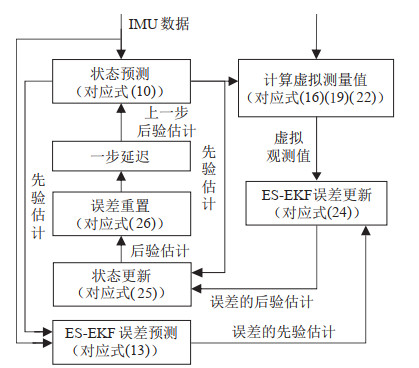
2 方法（Methodology） 2.1 总体框架

如图 1所示，融合算法总体框架包括子系统和融合估计器两大部分。子系统包括激光定位子系统、视觉定位子系统、全局速度测量子系统。其中，IMU姿态测量模块以重力方向或地磁方向作为参考，提供有绝对参考的俯仰角、滚转角等姿态信息，例如AHRS、垂直参考单元（VRU）等。移动机器人正运动学模型以编码器输出的轮速作为输入，求解出移动机器人参考点处的线速度，经IMU姿态分解后可得车体在世界坐标系中的运动速度，其观测模型详见2.4.3节。视觉定位子系统和激光定位子系统分别以图像和激光点云（也包括IMU数据）为输入，可输出移动机器人的位置、姿态等信息，其观测模型详见2.4.1和2.4.2节。ES-EKF估计器在结构上可以分为状态预测过程和状态更新过程，算法设计过程详见第2节。

图 2展示了基于ES-EKF的融合估计器的算法流程，其中，各模块的具体处理过程请参考其对应的公式。

2.2 姿态及其误差表示

设$ SO(3) $为3维姿态空间，姿态的矩阵表示、旋转向量表示分别记为$ {\mathit{\boldsymbol{R}}}\in SO(3) $和$ {\mathit{\boldsymbol{\theta}}} \in \mathbb{R}^{3} $，它们之间的转换关系记为

$ \begin{align} {\mathit{\boldsymbol{R}}}=\exp ({\mathit{\boldsymbol{\theta}}}^{\wedge}), \; \; \; \mathit{\boldsymbol{\theta}} = (\ln {\mathit{\boldsymbol{R}}})^{\vee} \end{align} $

(1)

式中，$ (\cdot)^{\wedge} $表示将向量映射为一个反对称矩阵^[21]，$ (\cdot)^{\wedge} $和$ (\cdot)^{\vee} $互为逆映射，即

$ \begin{align} {{\mathit{\boldsymbol{\theta}}}}^{\wedge} = \begin{bmatrix} 0 & {-\theta_{z}} & {\theta_{y}} \\ {\theta_{z}} & 0 & {-\theta_{x}} \\ {-\theta_{y}} & {\theta_{x}} & 0 \end{bmatrix}, \; \; \; ( \mathit{\boldsymbol{\theta}}^{\wedge} )^{\vee} =\mathit{\boldsymbol{\theta}} \end{align} $

(2)

2.3 系统模型与状态预测 2.3.1 状态变量定义

将系统状态$ {\mathit{\boldsymbol{x}}} $定义为

$ \begin{align} \mathit{\boldsymbol{x}} \triangleq [{\mathit{\boldsymbol{p}}, \mathit{\boldsymbol{v}}, \mathit{\boldsymbol{R}}, \mathit{\boldsymbol{b}}_{\rm a}, \mathit{\boldsymbol{b}}_{\rm g}}] \end{align} $

(3)

其中，位置$ \mathit{\boldsymbol{p}}\in \mathbb{R}^{3} $、姿态$ \mathit{\boldsymbol{R}}\in \mathbb{R}^{3} $、速度$ \mathit{\boldsymbol{v}}\in \mathbb{R}^{3} $定义在世界坐标系中，加速度计测量偏差$ \mathit{\boldsymbol{b}}_{\rm a} \in \mathbb{R}^{3} $，陀螺仪测量偏差$ \mathit{\boldsymbol{b}}_{\rm g} \in \mathbb{R}^{3} $定义在机器人坐标系中。对应的估计值记为

$ \begin{align} \hat{\mathit{\boldsymbol{x}}} \triangleq [\hat{\mathit{\boldsymbol{p}}}, \hat{\mathit{\boldsymbol{v}}}, \hat{\mathit{\boldsymbol{R}}}, \hat{\mathit{\boldsymbol{b}}}_{\rm a}, \hat{\mathit{\boldsymbol{b}}}_{\rm g}] \end{align} $

(4)

将状态估计误差$ {\mathit{\boldsymbol{\delta}}} $定义为真实值与估计值的偏差：

$ \begin{align} {\mathit{\boldsymbol{\delta}}} \triangleq [ {\mathit{\boldsymbol{\delta}}_{{\mathit{\boldsymbol{p}}}}^{\rm T}} , \; \; {\mathit{\boldsymbol{\delta}}_{{\mathit{\boldsymbol{v}}}}^{\rm T}} , \; \; {\mathit{\boldsymbol{\delta}}_{{\mathit{\boldsymbol{\theta}}}}^{\rm T}} , \; \; {\mathit{\boldsymbol{\delta}}_{{\mathit{\boldsymbol{b}}}{\rm a}}^{\rm T}} , \; \; {\mathit{\boldsymbol{\delta}}_{{\mathit{\boldsymbol{b}}}{\rm g}}^{\rm T}} ]^{\rm T}\in \mathbb{R}^{15} \end{align} $

(5)

各误差的定义式如下：

$ \begin{align} \begin{cases} {\mathit{\boldsymbol{\delta}}_{{\mathit{\boldsymbol{p}}}}\triangleq \mathit{\boldsymbol{p}}-\hat{\mathit{\boldsymbol{p}}}} \\ {\mathit{\boldsymbol{\delta}}_{{\mathit{\boldsymbol{v}}}}\triangleq \mathit{\boldsymbol{v}}-\hat{\mathit{\boldsymbol{v}}}} \\ {\mathit{\boldsymbol{\delta}}_{{\mathit{\boldsymbol{\theta}}}}\triangleq \ln (\hat{\mathit{\boldsymbol{R}}}^{\rm T}\mathit{\boldsymbol{R}})^{\vee}} \\ {\mathit{\boldsymbol{\delta}}_{{\mathit{\boldsymbol{b}}}{\rm a}}\triangleq \mathit{\boldsymbol{b}}_{\rm a} -\hat{\mathit{\boldsymbol{b}}}_{\rm a}} \\ {\mathit{\boldsymbol{\delta}}_{{\mathit{\boldsymbol{b}}}{\rm g}} \triangleq \mathit{\boldsymbol{b}}_{\rm g} -\hat{\mathit{\boldsymbol{b}}}_{\rm g}} \end{cases} \end{align} $

(6)

2.3.2 系统的状态运动模型

IMU的测量模型设为^[19]

$ \begin{align} \mathit{\boldsymbol{a}}_{\rm m} & =\mathit{\boldsymbol{a}}+\mathit{\boldsymbol{b}}_{\rm a} +\mathit{\boldsymbol{n}}_{\rm a} \end{align} $

(7)

$ \begin{align} \mathit{\boldsymbol{\omega}}_{\rm m} & =\mathit{\boldsymbol{\omega}} +\mathit{\boldsymbol{b}}_{\rm g} +\mathit{\boldsymbol{n}}_{\rm g} \end{align} $

(8)

其中，$ \mathit{\boldsymbol{a}}_{\rm m} \in \mathbb{R}^{3} $表示加速度计的测量输出，$ \mathit{\boldsymbol{a}}\in \mathbb{R}^{3} $为加速度真值，$ \mathit{\boldsymbol{n}}_{\rm a} \in \mathbb{R}^{3} $为加速度计的测量噪声；$ \mathit{\boldsymbol{\omega}}_{\rm m} \in \mathbb{R}^{3} $表示陀螺仪的测量输出，$ \mathit{\boldsymbol{\omega}} \in \mathbb{R}^{3} $为角速度真值，$ \mathit{\boldsymbol{n}}_{\rm g} \in \mathbb{R}^{3} $为陀螺仪的测量噪声。

将测量偏差$ {\mathit{\boldsymbol{b}}}_{\rm a} $和$ {\mathit{\boldsymbol{b}}}_{\rm g} $建模为随机游走模型^[9]，则系统的状态运动模型为

$ \begin{align} \begin{cases} \dot{\mathit{\boldsymbol{p}}}=\mathit{\boldsymbol{v}} \\ \dot{\mathit{\boldsymbol{v}}}=\mathit{\boldsymbol{R}}(\mathit{\boldsymbol{a}}_{\rm m}-\mathit{\boldsymbol{b}}_{\rm a}-\mathit{\boldsymbol{n}}_{\rm a})+\mathit{\boldsymbol{g}} \\ \dot{\mathit{\boldsymbol{R}}}=\mathit{\boldsymbol{R}}(\mathit{\boldsymbol{\omega}}_{\rm m}-\mathit{\boldsymbol{b}}_{\rm g}-\mathit{\boldsymbol{n}}_{\rm g})^{\wedge} \\ \dot{\mathit{\boldsymbol{b}}}_{\rm a}=\mathit{\boldsymbol{\tau}}_{\mathit{\boldsymbol{b}}\rm a} \\ \dot{\mathit{\boldsymbol{b}}}_{\rm g}=\mathit{\boldsymbol{\tau}}_{\mathit{\boldsymbol{b}}\rm g} \end{cases} \end{align} $

(9)

式中，$ {\mathit{\boldsymbol{g}}} $为重力加速度常量，$ {\mathit{\boldsymbol{n}}}_{\rm a} $、$ {\mathit{\boldsymbol{n}}}_{\rm g} $、$ {\mathit{\boldsymbol{\tau}}}_{{\mathit{\boldsymbol{b}}}{\rm a}} $、$ {\mathit{\boldsymbol{\tau}}}_{{\mathit{\boldsymbol{b}}}{\rm g}} $均建模为高斯白噪声，即$ \mathit{\boldsymbol{n}}_{\rm a} \sim {\mathscr{N}} ({\mathit{\boldsymbol{0}}, \sigma_{\rm a}^{2} {{\mathit{\boldsymbol{I}}}}_{3}}) $，$ \mathit{\boldsymbol{n}}_{\rm g} \sim {\mathscr{N}} ({\mathit{\boldsymbol{0}}, \sigma_{\rm g}^{2} {{\mathit{\boldsymbol{I}}}}_{3}}) $，$ \mathit{\boldsymbol{\tau}}_{{\mathit{\boldsymbol{b}}}{\rm a}} \sim {\mathscr{N}}({\mathit{\boldsymbol{0}}, \sigma_{{\mathit{\boldsymbol{b}}}{\rm a}}^{2} {{\mathit{\boldsymbol{I}}}}_{3}}) $，$ \mathit{\boldsymbol{\tau}}_{{\mathit{\boldsymbol{b}}}{\rm g}} \sim {\mathscr{N}}({\mathit{\boldsymbol{0}}, \sigma_{{\mathit{\boldsymbol{b}}}{\rm g}}^{2} {{\mathit{\boldsymbol{I}}}}_{3}}) $。

对微分方程(9) 在微小时间间隔$ \Delta t \triangleq t_{k} -t_{k-1} $内进行数值积分，得到系统模型的差分递推形式：

$ \begin{align} {\mathit{\boldsymbol{x}}}_{k} ={{\mathit{\boldsymbol{f}}}}({\mathit{\boldsymbol{x}}_{k-1}, \mathit{\boldsymbol{u}}_{{\rm m}, k-1}, \mathit{\boldsymbol{w}}_{\text{sys}, k}}) \end{align} $

(10)

其中，控制输入定义为$ \mathit{\boldsymbol{u}}_{{\rm m}, k-1} \triangleq [{\mathit{\boldsymbol{a}}_{{\rm m}, k-1}^{\rm T}}, \; \; {{\mathit{\boldsymbol{\omega}}}_{{\rm m}, k-1}^{\rm T}} ]^{\rm T} $，系统的过程噪声定义为$ \mathit{\boldsymbol{w}}_{\text{sys}, k} \triangleq [{\mathit{\boldsymbol{n}}}_{\rm a}^{\rm T}, \; \; {\mathit{\boldsymbol{n}}}_{\rm g}^{\rm T} , \; \; {\mathit{\boldsymbol{\tau}}}_{{\mathit{\boldsymbol{b}}}{\rm a}}^{\rm T}, \; \; {\mathit{\boldsymbol{\tau}}}_{{\mathit{\boldsymbol{b}}}{\rm g}}^{\rm T}]^{\rm T} $。

2.3.3 系统的误差运动模型

根据误差定义式(6)和系统微分方程(9)，可得误差状态的微分方程^[19]：

$ \begin{align} \mathit{\boldsymbol{\dot{\delta}}}={\mathit{\boldsymbol{A}}}{\mathit{\boldsymbol{\delta}}} +{\mathit{\boldsymbol{B}}}\mathit{\boldsymbol{w}}_{\text{sys}, k} \end{align} $

(11)

式中，

$ \begin{align*} {\mathit{\boldsymbol{A}}} & =\begin{bmatrix} {\mathit{\boldsymbol{0}}_{3}} & {{{\mathit{\boldsymbol{I}}}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} \\ {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {-\hat{\mathit{\boldsymbol{R}}}({\mathit{\boldsymbol{a}}_{\rm m} -\hat{\mathit{\boldsymbol{b}}}_{\rm a}})^{\wedge}} & {-\hat{\mathit{\boldsymbol{R}}}} & {\mathit{\boldsymbol{0}}_{3}} \\ {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {-({{\mathit{\boldsymbol{\omega}}}_{\rm m} -\hat{\mathit{\boldsymbol{b}}}_{\rm g}})^{\wedge}} & {\mathit{\boldsymbol{0}}_{3}} & -{{{\mathit{\boldsymbol{I}}}}_{3}} \\ {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} \\ {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} \end{bmatrix}\\ {\mathit{\boldsymbol{B}}} & =\begin{bmatrix} {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} \\ {-\hat{\mathit{\boldsymbol{R}}}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} \\ {\mathit{\boldsymbol{0}}_{3}} & {-{{\mathit{\boldsymbol{I}}}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} \\ {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {{{\mathit{\boldsymbol{I}}}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} \\ {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {{{\mathit{\boldsymbol{I}}}}_{3}} \end{bmatrix} \end{align*} $

对微分方程(11) 在$ \Delta t $上进行数值积分，可得误差状态的运动模型为^[21]

$ \begin{align} \mathit{\boldsymbol{\delta}}_{k} ={\mathit{\boldsymbol{F}}}_{k, k-1} \mathit{\boldsymbol{\delta}}_{k-1} +{\mathit{\boldsymbol{C}}}_{k} \mathit{\boldsymbol{w}}_{\text{sys}, k} \end{align} $

(12)

式中，

$ \begin{align*} {\mathit{\boldsymbol{F}}}_{k, k-1} & ={\rm e}^{{\mathit{\boldsymbol{A}}}_{k-1} {\Delta} t}\approx {{\mathit{\boldsymbol{I}}}}_{15} +{\mathit{\boldsymbol{A}}}_{k-1} {\Delta} t+\frac{1}{2}({{\mathit{\boldsymbol{A}}}_{k-1} {\Delta} t})^{2} \\ {\mathit{\boldsymbol{C}}}_{k} & =\begin{bmatrix} {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} \\ {{\Delta} t{{\mathit{\boldsymbol{I}}}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} \\ {\mathit{\boldsymbol{0}}_{3}} & {{\Delta} t{{\mathit{\boldsymbol{I}}}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} \\ {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\sqrt{{\Delta} t}{{\mathit{\boldsymbol{I}}}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} \\ {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\sqrt{{\Delta} t}{{\mathit{\boldsymbol{I}}}}_{3}} \end{bmatrix} \\ \mathit{\boldsymbol{w}}_{\text{sys}, k} & \sim {\mathscr{N}}({\mathit{\boldsymbol{0}}_{12\times 1}, \mathit{\boldsymbol{\varSigma}}_{\text{sys}}}) \\ \mathit{\boldsymbol{\varSigma}}_{\text{sys}} & ={\text{diag}}({\sigma_{\rm a}^{2} {{\mathit{\boldsymbol{I}}}}_{3}, \sigma_{\rm g}^{2} {{\mathit{\boldsymbol{I}}}}_{3}, \sigma_{{\mathit{\boldsymbol{b}}}{\rm a}}^{2} {{\mathit{\boldsymbol{I}}}}_{3}, \sigma_{{\mathit{\boldsymbol{b}}}{\rm g}}^{2} {{\mathit{\boldsymbol{I}}}}_{3}}) \end{align*} $

2.3.4 状态预测与误差预测

在上一时刻，状态、误差状态及其协方差矩阵的后验估计分别记为$ \hat{\mathit{\boldsymbol{x}}}_{k-1}^{+} $、$ \hat{\mathit{\boldsymbol{\delta}}}_{k-1}^{+} $和$ {\mathit{\boldsymbol{P}}}_{k-1}^{+} $；在当前时刻，状态、误差状态及其协方差矩阵的先验估计分别记为$ \hat{\mathit{\boldsymbol{x}}}_{k}^{-} $、$ \hat{\mathit{\boldsymbol{\delta}}}_{k}^{-} $和$ {\mathit{\boldsymbol{P}}}_{k}^{-} $；则在卡尔曼滤波框架下，可得状态和误差的预测式：

$ \begin{align} \hat{\mathit{\boldsymbol{x}}}_{k}^{-} & ={{\mathit{\boldsymbol{f}}}} (\hat{\mathit{\boldsymbol{x}}}_{k-1}^{+}, \mathit{\boldsymbol{u}}_{{\rm m}, k-1}, \mathit{\boldsymbol{0}} ) \\ \hat{\mathit{\boldsymbol{\delta}}}_{k}^{-} & =\mathit{\boldsymbol{F}}_{k, k-1} \hat{\mathit{\boldsymbol{\delta}}}_{k-1}^{+} \\ \mathit{\boldsymbol{P}}_{k}^{-} & =\mathit{\boldsymbol{F}}_{k, k-1} \mathit{\boldsymbol{P}}_{k-1}^{+} \mathit{\boldsymbol{F}}_{k, k-1}^{{\rm T}}+\mathit{\boldsymbol{C}}_{k} {\boldsymbol \varSigma}_{\text{sys}} \mathit{\boldsymbol{C}}_{k}^{{\rm T}} \end{align} $

(13)

2.4 观测模型与状态更新 2.4.1 激光定位子系统观测模型

在总结Kubelka^[11]和Ma^[21]的工作基础上，进一步将位置增量$ {\mathit{\boldsymbol{y}}}_{\Delta {\mathit{\boldsymbol{p}}}, k} \in \mathbb{R}^{3} $和姿态增量$ \mathit{\boldsymbol{y}}_{\delta {\mathit{\boldsymbol{R}}}, k} $ $ \in SO(3) $的协方差建模为时间增量的2次函数，建立增量的测量模型为

$ \begin{equation} \begin{aligned} {\mathit{\boldsymbol{y}}}_{\delta {\mathit{\boldsymbol{R}}}, k} & =\hat{\mathit{\boldsymbol{R}}}_{k-1}^{+{\rm T}} {\mathit{\boldsymbol{R}}}_{k} \exp ({({{\mathit{\boldsymbol{w}}}_{\delta {\mathit{\boldsymbol{R}}}, k} {\Delta} t})^{\wedge}}) \\ {\mathit{\boldsymbol{y}}}_{\Delta {\mathit{\boldsymbol{p}}}, k} & =\hat{\mathit{\boldsymbol{R}}}_{k-1}^{+{\rm T}} ({{\mathit{\boldsymbol{p}}}_{k} -\hat{\mathit{\boldsymbol{p}}}_{k-1}^{+}})+{\mathit{\boldsymbol{w}}}_{\Delta {\mathit{\boldsymbol{p}}}, k} {\Delta} t \end{aligned} \end{equation} $

(14)

其中，$ {\mathit{\boldsymbol{w}}}_{\delta \mathit{\boldsymbol{R}}, k} \in \mathbb{R}^{3} $和$ {\mathit{\boldsymbol{w}}}_{\Delta \mathit{\boldsymbol{p}}, k} \in \mathbb{R}^{3} $分别为姿态增量测量噪声和位置增量测量噪声，这里均假设为高斯白噪声，协方差分别设为$ \sigma_{\Delta {\mathit{\boldsymbol{p}}}}^{2} {{\mathit{\boldsymbol{I}}}}_{3} $和$ \sigma_{\delta {\mathit{\boldsymbol{R}}}}^{2} {{\mathit{\boldsymbol{I}}}}_{3} $。

记激光定位子系统在时刻$ t_{k-1} $和$ t_{k} $输出的位置测量结果分别为$ {\mathit{\boldsymbol{p}}}_{{\rm m}, k-1} \in \mathbb{R}^{3} $和$ {\mathit{\boldsymbol{p}}}_{{\rm m}, k} \in \mathbb{R}^{3} $，姿态测量结果分别为$ {\mathit{\boldsymbol{R}}}_{{\rm m}, k-1} \in SO(3) $和$ {\mathit{\boldsymbol{R}}}_{{\rm m}, k} \in SO(3) $，定义虚拟测量值$ {\mathit{\boldsymbol{z}}}_{{\text{pi}}, k} \in \mathbb{R}^{6} $：

$ \begin{align} {\mathit{\boldsymbol{z}}}_{{\text{pi}}, k} \triangleq \begin{bmatrix} {{\mathit{\boldsymbol{R}}}_{{\rm m}, k-1}^{\rm T} ({{\mathit{\boldsymbol{p}}}_{{\rm m}, k} -{\mathit{\boldsymbol{p}}}_{{\rm m}, k-1}})-\hat{\mathit{\boldsymbol{R}}}_{k-1}^{+{\rm T}} ({\hat{\mathit{\boldsymbol{p}}}_{k}^{-} -\hat{\mathit{\boldsymbol{p}}}_{k-1}^{+}})} \\ {\ln (\hat{\mathit{\boldsymbol{R}}}_{k}^{-{\rm T}} \hat{\mathit{\boldsymbol{R}}}_{k-1}^{+} {\mathit{\boldsymbol{R}}}_{{\rm m}, k-1}^{\rm T} {\mathit{\boldsymbol{R}}}_{{\rm m}, k})^{\vee}} \end{bmatrix} \end{align} $

(15)

建立虚拟测量的观测模型如下：

$ \begin{align} {\mathit{\boldsymbol{z}}}_{{\text{pi}}, k} ={\mathit{\boldsymbol{H}}}_{{\text{pi}}, k} \mathit{\boldsymbol{\delta}}_{k} +{\mathit{\boldsymbol{D}}}_{{\text{pi}}, k} {\mathit{\boldsymbol{w}}}_{{\text{pi}}, k} \end{align} $

(16)

其中，

$ \begin{align*} & {\mathit{\boldsymbol{H}}}_{{\text{pi}}, k} =\begin{bmatrix} {\hat{\mathit{\boldsymbol{R}}}_{k-1}^{+{\rm T}}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} \\ {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {{{\mathit{\boldsymbol{I}}}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} \end{bmatrix} \\ & {\mathit{\boldsymbol{D}}}_{{\text{pi}}, k} =\begin{bmatrix} {{\Delta} t{{\mathit{\boldsymbol{I}}}}_{3}} & {\mathit{\boldsymbol{0}}_{3}} \\ {\mathit{\boldsymbol{0}}_{3}} & {{\Delta} t{{\mathit{\boldsymbol{I}}}}_{3}} \end{bmatrix} \\ & {\mathit{\boldsymbol{w}}}_{{\text{pi}}, k} \sim \mathit{\boldsymbol{{\mathscr{N}}}}({\mathit{\boldsymbol{0}}_{6\times 1}, {\text{diag}}({\sigma_{\Delta {\mathit{\boldsymbol{p}}}}^{2} {{\mathit{\boldsymbol{I}}}}_{3}, \sigma_{\delta {\mathit{\boldsymbol{R}}}}^{2} {{\mathit{\boldsymbol{I}}}}_{3}})}) \end{align*} $

2.4.2 视觉定位子系统观测模型

视觉定位子系统可同时输出位置、姿态及速度信息，其位姿观测模型与激光位姿观测模型完全一样，不再赘述，这里仅介绍其局部速度观测模型。

在机器人坐标系中，设时刻$ t_{k} $的局部速度测量模型为

$ \begin{align} {\mathit{\boldsymbol{y}}}_{{\text{lv}}, k} ={\mathit{\boldsymbol{R}}}_{k}^{\rm T} {\mathit{\boldsymbol{v}}}_{k} +{\mathit{\boldsymbol{w}}}_{{\text{lv}}, k} \end{align} $

(17)

其中，$ {\mathit{\boldsymbol{w}}}_{{\text{lv}}, k} \in \mathbb{R}^{3} $为局部速度测量噪声，协方差设为$ \sigma_{\text{lv}}^{2} {{\mathit{\boldsymbol{I}}}}_{3} $。

记视觉定位子系统在时刻$ t_{k} $输出的局部速度测量值为$ {\mathit{\boldsymbol{v}}}_{{\rm lv, m}, k} \in \mathbb{R}^{3} $，参考系为机器人坐标系，定义虚拟测量值$ {\mathit{\boldsymbol{z}}}_{{\text{lv}}, k} \in \mathbb{R}^{3} $：

$ \begin{align} {\mathit{\boldsymbol{z}}}_{{\text{lv}}, k} \triangleq {\mathit{\boldsymbol{v}}}_{{\rm lv, m}, k} -\hat{\mathit{\boldsymbol{R}}}_{k}^{-{\rm T}} \hat{\mathit{\boldsymbol{v}}}_{k}^{-} \end{align} $

(18)

建立虚拟测量值的观测模型如下：

$ \begin{align} {\mathit{\boldsymbol{z}}}_{{\text{lv}}, k} ={\mathit{\boldsymbol{H}}}_{{\text{lv}}, k} \mathit{\boldsymbol{\delta}}_{k} +{\mathit{\boldsymbol{D}}}_{{\text{lv}}, k} {\mathit{\boldsymbol{w}}}_{{\text{lv}}, k} \end{align} $

(19)

其中，

$ \begin{align*} {\mathit{\boldsymbol{H}}}_{{\text{lv}}, k} & =[ {\mathit{\boldsymbol{0}}_{3}} \; \; {\hat{\mathit{\boldsymbol{R}}}_{k}^{-{\rm T}}} \; \; {({\hat{\mathit{\boldsymbol{R}}}_{k}^{-{\rm T}} \hat{\mathit{\boldsymbol{v}}}_{k}^{-}})^{\wedge}} \; \; {\mathit{\boldsymbol{0}}_{3}} \; \; {\mathit{\boldsymbol{0}}_{3}} \; \; {\mathit{\boldsymbol{0}}_{3}} ] \\ {\mathit{\boldsymbol{D}}}_{{\text{lv}}, k} & ={{\mathit{\boldsymbol{I}}}}_{3} \\ {\mathit{\boldsymbol{w}}}_{{\text{lv}}, k} & \sim \mathit{\boldsymbol{\mathscr{N}}}({\mathit{\boldsymbol{0}}_{3\times 1}, \sigma_{\text{lv}}^{2} {{\mathit{\boldsymbol{I}}}}_{3}}) \end{align*} $

2.4.3 全局速度测量子系统观测模型

在世界坐标系中，设时刻$ t_{k} $的全局速度测量模型为

$ \begin{align} {\mathit{\boldsymbol{y}}}_{{\text{gv}}, k} ={\mathit{\boldsymbol{v}}}_{k} +{\mathit{\boldsymbol{w}}}_{{\text{gv}}, k} \end{align} $

(20)

其中，$ {\mathit{\boldsymbol{w}}}_{{\text{gv}}, k} \in \mathbb{R}^{3} $为世界坐标系内的速度测量噪声，协方差设为$ \sigma_{\text{gv}}^{2} {{\mathit{\boldsymbol{I}}}}_{3} $。

记IMU姿态测量模块的输出为$ {\mathit{\boldsymbol{C}}}_{{\rm m}, k} \in SO(3) $，正运动学模块利用编码器读数解算出的机器人速度为$ {\mathit{\boldsymbol{v}}}_{{\rm m}, k} \in \mathbb{R}^{3} $，定义虚拟测量值$ {\mathit{\boldsymbol{z}}}_{{\text{gv}}, k} \in \mathbb{R}^{3} $：

$ \begin{align} {\mathit{\boldsymbol{z}}}_{{\text{gv}}, k} \triangleq {\mathit{\boldsymbol{C}}}_{{\rm m}, k} {\mathit{\boldsymbol{v}}}_{{\rm m}, k} -\hat{\mathit{\boldsymbol{v}}}_{k}^{-} \end{align} $

(21)

建立虚拟测量值的观测模型如下：

$ \begin{align} {\mathit{\boldsymbol{z}}}_{{\text{gv}}, k} ={\mathit{\boldsymbol{H}}}_{{\text{gv}}, k} \mathit{\boldsymbol{\delta}}_{k} +{\mathit{\boldsymbol{D}}}_{{\text{gv}}, k} {\mathit{\boldsymbol{w}}}_{{\text{gv}}, k} \end{align} $

(22)

其中，

$ \begin{align*} & {\mathit{\boldsymbol{H}}}_{{\text{gv}}, k} =\left[ {\mathit{\boldsymbol{0}}_{3}} \; \; {{{\mathit{\boldsymbol{I}}}}_{3}} \; \; {\mathit{\boldsymbol{0}}_{3}} \; \; {\mathit{\boldsymbol{0}}_{3}} \; \; {\mathit{\boldsymbol{0}}_{3}} \; \; {\mathit{\boldsymbol{0}}_{3}} \right] \\ & {\mathit{\boldsymbol{D}}}_{{\text{gv}}, k} ={{\mathit{\boldsymbol{I}}}}_{3} \\ & {\mathit{\boldsymbol{w}}}_{{\text{gv}}, k} \sim \mathit{\boldsymbol{{\mathscr{N}}}}({\mathit{\boldsymbol{0}}_{3\times 1}, \sigma_{\text{gv}}^{2} {{\mathit{\boldsymbol{I}}}}_{3}}) \end{align*} $

2.4.4 误差更新与状态更新

为了便于表示，将观测模型统一表示为

$ \begin{equation} \begin{aligned} {\mathit{\boldsymbol{z}}}_{k} & ={\mathit{\boldsymbol{H}}}_{k} \mathit{\boldsymbol{\delta}}_{k} +{\mathit{\boldsymbol{D}}}_{k} {\mathit{\boldsymbol{w}}}_{{\text{meas}}, k} \\ {\mathit{\boldsymbol{w}}}_{{\text{meas}}, k} & \sim {\mathscr{N}}(\mathit{\boldsymbol{0}}, \mathit{\boldsymbol{\varSigma}}_{{\text{meas}}, k}) \end{aligned} \end{equation} $

(23)

其中，$ {\mathit{\boldsymbol{H}}}_{k} $、$ {\mathit{\boldsymbol{D}}}_{k} $和$ \mathit{\boldsymbol{\varSigma}}_{{\text{meas}}, k} $分别表示第$ k $时刻的观测矩阵、噪声矩阵和协方差矩阵。

在当前时刻，状态、误差状态及其协方差矩阵的后验估计分别记为$ \hat{\mathit{\boldsymbol{x}}}_{k}^{+} $、$ \hat{\mathit{\boldsymbol{\delta}}}_{k}^{+} $和$ {\mathit{\boldsymbol{P}}}_{k}^{+} $；则在卡尔曼框架下，可得状态和误差的观测更新式：

$ \begin{equation} \begin{aligned} \mathit{\boldsymbol{K}}_{k} & =\mathit{\boldsymbol{P}}_{k}^{-} \mathit{\boldsymbol{H}}_{k}^{\rm T} (\mathit{\boldsymbol{H}}_{k} \mathit{\boldsymbol{P}}_{k}^{-} \mathit{\boldsymbol{H}}_{k}^{\rm T} +{\mathit{\boldsymbol{D}}}_{k} \mathit{\boldsymbol{\varSigma}}_{\text{meas}, k} {\mathit{\boldsymbol{D}}}_{k}^{\rm T})^{-1} \\ \hat{\mathit{\boldsymbol{\delta}}}_{k}^{+} & =\hat{\mathit{\boldsymbol{\delta}}}_{k}^{-} +\mathit{\boldsymbol{K}}_{k} ({\mathit{\boldsymbol{z}}}_{k} -{\mathit{\boldsymbol{H}}}_{k} \hat{\mathit{\boldsymbol{\delta}}}_{k}^{-}) \\ \mathit{\boldsymbol{P}}_{k}^{+} & =({{\mathit{\boldsymbol{I}}}}_{15} -\mathit{\boldsymbol{K}}_{k} \mathit{\boldsymbol{H}}_{k})\mathit{\boldsymbol{P}}_{k}^{-} \\ \hat{\mathit{\boldsymbol{x}}}_{k}^{+} & =\hat{\mathit{\boldsymbol{x}}}_{k}^{-} \boxplus \hat{\mathit{\boldsymbol{\delta}}}_{k}^{+} \end{aligned} \end{equation} $

(24)

式中，运算符$ \boxplus $表示利用误差后验估计值$ \hat{\mathit{\boldsymbol{\delta}}}_{k}^{+} $对状态先验估计值$ \hat{\mathit{\boldsymbol{x}}}_{k}^{-} $进行补偿，具体计算公式如下：

$ \begin{align} \begin{cases} {\mathit{\boldsymbol{p}}_{k}^{+} = \mathit{\boldsymbol{p}}_{k}^{-} +\hat{\mathit{\boldsymbol{\delta}}}_{{\mathit{\boldsymbol{p}}}, k}^{+}} \\ {\mathit{\boldsymbol{v}}_{k}^{+} = \mathit{\boldsymbol{v}}_{k}^{-} +\hat{\mathit{\boldsymbol{\delta}}}_{{\mathit{\boldsymbol{v}}}, k}^{+}} \\ {\mathit{\boldsymbol{R}}_{k}^{+} = \mathit{\boldsymbol{R}}_{k}^{-} \exp ({\hat{\mathit{\boldsymbol{\delta}}}_{{\mathit{\boldsymbol{a}}}, k}^{+\wedge}})} \\ {\mathit{\boldsymbol{b}}_{{\rm a}, k}^{+} = \mathit{\boldsymbol{b}}_{{\rm a}, k}^{-} +\hat{\mathit{\boldsymbol{\delta}}}_{{\mathit{\boldsymbol{b}}}{\rm a}, k}^{+}} \\ {\mathit{\boldsymbol{b}}_{{\rm g}, k}^{+} = \mathit{\boldsymbol{b}}_{{\rm g}, k}^{-} +\hat{\mathit{\boldsymbol{\delta}}}_{{\mathit{\boldsymbol{b}}}{\rm g}, k}^{+}} \end{cases} \end{align} $

(25)

最后，对误差状态的后验估计值进行归零重置，为下一次滤波估计过程做准备，归零过程记为

$ \begin{align} \hat{\mathit{\boldsymbol{\delta}}}_{k}^{+} \leftarrow \mathit{\boldsymbol{0}}_{15\times 1} \end{align} $

(26)

3 实验（Experiments） 3.1 实验平台搭建

硬件平台由3部分构成：(1) 四轮独立驱动越野型移动机器人；(2) 传感器集合；(3) 工控机。移动机器人及其传感器配置情况如图 3所示。

移动机器人为AgileX SCOUT2.0，工控机为NVIDIA Jetson AGX Xavier，工控机通过CAN（控制器局域网络）接口与移动机器人下位机通信，实时获取底盘的轮胎转速、线速度等运动状态信息。传感器产品包括：轮式编码器（SCOUT2.0自带）、惯性测量单元（Xsens MTi-30）、双目视觉传感器（Stereolabs ZED 2）、激光雷达（RoboSense RS-LiDAR-16）、RTK接收机（司南导航M600mini-G GNSS-RTK接收机），各传感器产品的输出参数见表 1。

整个导航系统在ROS环境下使用C$ ++ $语言编程实现，其中，激光定位子系统改编自LeGO-LOAM^[7]开源算法包，视觉定位子系统算法改编自VINS-Fusion^[9]开源算法包。表 2展示了系统各模块的输出频率。

3.2 测试及其评估

为了充分验证本文融合定位算法的有效性，分别在街道场景和野外场景下完成定位测试，表 3列出了各实验场景中移动机器人的基本运动情况。

实验中，将各传感器数据采集下来，分别进行了如下定位算法测试：(1) 利用VINS-Fusion算法^[9]进行IMU/相机融合定位；(2) 利用LeGO-LOAM算法^[7]进行IMU/激光雷达融合定位；(3) 利用robot-localization算法^[12]进行IMU/编码器/相机/激光雷达融合定位；(4) 利用本文的IEVL-Fusion算法进行IMU/编码器/相机/激光雷达融合定位；(5) 利用本文的IEVL-Fusion-no算法进行IMU/编码器/相机/激光雷达融合定位。IEVL-Fusion-no算法是将IEVL-Fusion算法中编码器全局式融合替换为局部式融合后得到的算法，其余部分均与IEVL-Fusion算法相同。各定位算法的文献来源及其所用传感器组合如表 4所示。

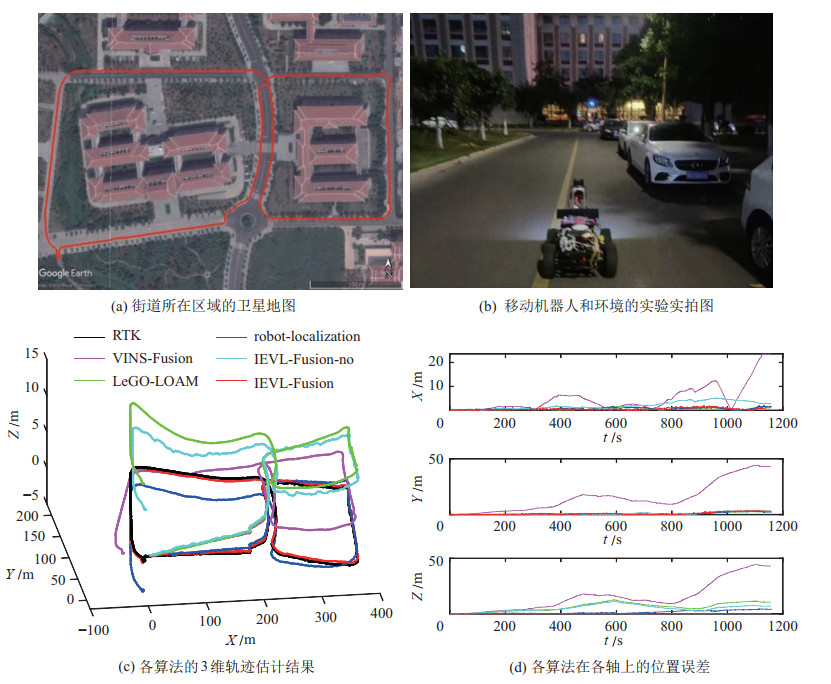
图 4展示了街道实验中相关的照片和定位曲线。街道数据采集于晚上6点左右，光线由明变暗，移动机器人总的行驶路程约为1419 m，高度变化约2.5 m，行驶时长约1158 s，平均速度约1.23 m/s。图 4(a)为街道所在区域的卫星地图，红色曲线为RTK参考轨迹，移动机器人绕着两栋教学大楼走出了一个“8”形，其中约有1/4的石板路，另外3/4为柏油路。图 4(b)为实验过程中实拍到的移动机器人和环境的照片，此时的光线昏暗，马路旁路灯已经打开。图 4(c)为各算法的3维轨迹估计结果，对比来看，IEVL-Fusion算法的结果更加接近RTK给出的参考轨迹。图 4(d)为各算法在$ X $、$ Y $、$ Z $分量上的定位误差关于时间的变化曲线。

图 5展示了野外实验中相关的照片和定位曲线。野外数据采集的时间在下午2:30左右，移动机器人总的行驶路程约为529 m，高度变化约35 m，行驶时长约619 s，平均速度约0.85 m/s。图 5(a)为实验所在区域的卫星地图，红色曲线为RTK参考轨迹，移动机器人沿着非常崎岖的土路曲折前行，道路两旁为自然生长的植被。图 5(b)为实验过程中实拍到的移动机器人和周围环境的照片，可以看到，这样的场景在野外是普遍存在的。图 5(c)为各算法的3维轨迹估计结果，IEVL-Fusion-no、IEVL-Fusion和robot-localization算法的定位轨迹均有较好的收敛。图 5(d)为各算法的$ X $分量、$ Y $分量和$ Z $分量的定位误差关于时间的变化曲线，从曲线变化很难直观看出定位效果，需要进一步定量分析。

实验过程中RTK接收机的数据接收正常，本文依据RTK定位数据对测试结果进行量化与评价。为了对定位结果进行综合评估，本文定义了4个量化指标：最大定位误差ME、最大相对定位误差MRE、平均定位误差AE和平均相对定位误差ARE^[11]：

$ \begin{align} \begin{cases} {\rm ME}= \max \{\|\hat{\mathit{\boldsymbol{p}}}_{i}-\mathit{\boldsymbol{p}}_{i}^{{\rm RTK}}\|\}_{i=1}^{N}, & {\rm MRE}=\dfrac{{\rm ME}}{D} \times 100 \% \\ {\rm AE}= \frac{1}{N} \sum\limits_{i=1}^{N}\|\hat{\mathit{\boldsymbol{p}}}_{i}-\mathit{\boldsymbol{p}}_{i}^{{\rm RTK}}\|, & {\rm ARE}=\dfrac{{\rm AE}}{D} \times 100 \% \end{cases} \end{align} $

(27)

其中，$ N $表示采样点的个数，$ D $表示机器人运动的路程。

依据以上定义的量化指标，对各算法的$ X $、$ Y $、$ Z $三个分量和总体（3D位置）进行指标计算，计算结果列于表 5中，其中加粗的字体表示对应列中的最小值。

就总体定位误差而言，IEVL-Fusion在ME、MRE、AE和ARE四个指标上均为最好，平均相对定位误差小于总路程的0.4%，最大相对定位误差小于0.7%。相较于VINS-Fusion、LeGO-OAM、robot-localization和IEVL-Fusion-no算法，IEVL-Fusion算法的最大相对定位误差分别降低了约90%、65%、40% 和40%。

对比各算法在$ X $和$ Y $分量上的定位误差可看出，IEVL-Fusion算法的水平定位精度和LeGO-LOAM算法相当。但在$ Z $分量上，IEVL-Fusion算法具有最小的定位误差，且IEVL-Fusion算法的平均定位误差相较于VINS-Fusion、LeGO-LOAM、robot-localization以及IEVL-Fusion-no算法分别降低了86%、83%、72% 和42% 以上。

实际上，偏航角$ \psi $、俯仰角$ \theta $、滚转角$ \phi $与旋转矩阵$ {\mathit{\boldsymbol{R}}} $之间存在如下关系：

$ \begin{align} {\mathit{\boldsymbol{R}}} =\begin{bmatrix} * & * & * \\ * & * & * \\ {-{\sin}{\theta }} & {{\cos}{\theta } {\sin}{\phi}} & {{\cos \phi} \cos \phi} \end{bmatrix} \end{align} $

(28)

其中，$ * $表示与$ \psi $有关的项。AHRS输出的俯仰角和滚转角是以重力向量为参考求解到的，偏航角是以地磁为参考的。根据全局速度观测模型(21)，全局速度$ {\mathit{\boldsymbol{C}}}_{{\rm m}, k} \mathit{\boldsymbol{v}}_{{\rm m}, k} $的第3个分量是有绝对参考的竖直速度测量值，第1个分量和第2个分量易受到周围环境中电磁干扰的影响，无法提供无偏的速度测量值。这一分析与实验结果相互印证，即全局速度观测更新对于竖直方向上的误差累积具有显著的抑制作用。

4 结论与展望（Conclusion and prospect）

针对卫星拒止环境中移动机器人高精度定位的需求，提出一种基于ES-EKF的激光定位子系统/视觉定位子系统/全局速度测量子系统松耦合融合定位方法，设计了一个误差漂移低、输出频率高的IMU/编码器/相机/激光组合定位系统，并在城镇和野外场景下进行了测试。相较于VINS-Fusion、LeGO-LOAM、robot-localization等定位算法，本文提出的方法具有更高的定位精度。本文方法的主要优势为：(1) 无需对整个定位系统进行重复设计即可实现LeGO-LOAM、VINS-Fusion算法在组合导航中的快速集成和应用；(2) 将位姿融合转化为位姿增量融合，避免了激光定位系统中位姿协方差无法建模的问题；(3) 利用IMU和编码器分解得到机器人的全局速度测量值，对状态估计器的高度估计产生有效约束，显著提高整个系统的状态估计精度。

在实际的移动机器人导航中，除了努力提高定位系统的精度之外，还希望提升复杂环境下移动机器人的定位鲁棒性和持续性^[22]。例如，遮挡、逆光等会造成视觉定位算法失效，长廊会造成激光定位算法失效^[23-24]。因此，在接下来的研究中，将进一步利用多传感器融合技术赋予系统处理这些问题的能力，提升整个定位系统的定位可靠性。