同时定位与地图构建(simultaneous localization and mapping,SLAM)是移动机器人实现自主导航和完成复杂环境交互任务的基础。RGB-D相机可以直接采集彩色和深度图像且成本较低,因此基于RGB-D相机的视觉SLAM系统被广泛应用于室内移动机器人等领域。室内场景常常包含各种运动物体,对SLAM系统会产生位姿估计和地图构建两方面的干扰[1-2]。
现有的视觉SLAM系统大部分都假设场景为静态,并根据这一假设简化位姿估计。这些SLAM算法将动态特征点加入位姿计算,在稀疏点云地图中生成对应的错误地图点,导致位姿估计产生偏差。因此,需要一种有效方法区分动态特征或区域。运动物体还将影响SLAM系统的稠密建图,错误的位姿估计使得算法错误叠加多帧观测信息,造成地图扭曲。即便位姿估计正确,同一运动物体在不同时刻的信息被多次加入地图将形成物体运动的“残影”,无法正确反映场景的真实状态。
光流法是研究帧间运动变化的常用方法。Sun等[3]通过稠密光流和CodeBook模型分割动态区域,排除动态特征干扰,建立稠密点云。Wang等[4]对图像计算稠密光流,结合点轨迹聚类得到动态区域分割。场景流方法将2维光流的思想引入到3维空间中,计算3维空间位移。Lee等[5]计算场景流,建立刚体运动模型,分割运动刚体区域。稠密光流和场景流方法对于动态区域的分割效果好,但对大量像素点进行光流计算将降低算法的实时性。
采用其他方法同样存在运算效率与动态分割、稠密建图之间的矛盾。Sun等[6]对相邻图像帧进行背景配准,采用帧间差分法识别运动,利用深度图量化分割动态区域,不涉及稠密建图。高成强等[7]使用单高斯模型(single Gaussian model,SGM)对背景进行建模,建立稠密TSDF(截断符号距离函数)地图,但仅能得出运动物体的矩形框选。魏彤等[8]根据对极几何原理筛选动态特征点,并结合超像素分割算法标记动态区域,但分割计算量较大,降低了系统的实时性且不涉及稠密建图。张慧娟等[9]利用环境中的直线特征代替点特征,采用计算静态权重方法剔除动态线特征,计算效率高但不适用于稠密建图。文[10]提出基于改进几何与运动约束的算法,同样基于稀疏特征,因此不具备运动区域分割与在线稠密建图的能力。
除此之外,越来越多的研究者将深度学习方法应用到动态场景的SLAM算法中。Bescos等[11]利用Mask R-CNN网络[12]分割动态物体并借助过去时刻的关键帧对当前画面中缺失的背景进行填充以便进行稠密建图,Yu等[13]则利用SegNet网络[14]对图像进行分割和稠密建图。也有研究者选择使用目标检测网络先确定动态物体位置,再使用其他方法进行分割。Zhong等[15]通过目标检测网络和GrabCut算法[16]分割动态物体。姚二亮等[17]使用YOLOv3算法[18]初步滤除动态区域后通过图像中边缘的距离变换误差和光度误差的一致性评估更加细致地分割和滤除动态区域。Liu等[19]将YOLOv3与基于光流法的极线约束算法结合去除动态特征,位姿精度高但不涉及动态分割与稠密建图。基于深度学习的方法能够准确识别物体,通常表现良好,但无法识别不在网络先验范围内的动态物体且计算量大、依赖GPU硬件,难以应用在移动机器人等平台上。
综上所述,定位精度高且具有分割与稠密建图能力的方法往往计算效率不够理想。为解决这一问题,针对室内动态场景移动机器人,本文提出一种RGB-D SLAM方法,同时具有以下特点:
(1) 消除动态场景干扰,定位精度高;
(2) 计算效率高;
(3) 分割和标记动态物体;
(4) 在线稠密建图。
本文提出网格分割方法代替像素级分割,引入单应运动补偿与根据光流理论设计的双向补偿光流法,结合几何连通性处理与深度值聚类进行逐帧动态区域分割,避免动态特征点参与位姿优化,并大幅提升计算速度。同时构建稀疏点云地图和静态八叉树地图并进行耦合,在关键帧上使用基于网格分割和八叉树地图光线遍历的方法筛选静态地图点,更新稀疏点云地图,保障定位精度。
2 系统框架(System frame)本文提出的SLAM算法是在ORB-SLAM3算法[20]基础上进行改进,构建基于网格分割的位姿跟踪、稀疏点云建图与双地图耦合、八叉树建图、回环检测的四线程结构。图 1为系统流程图。
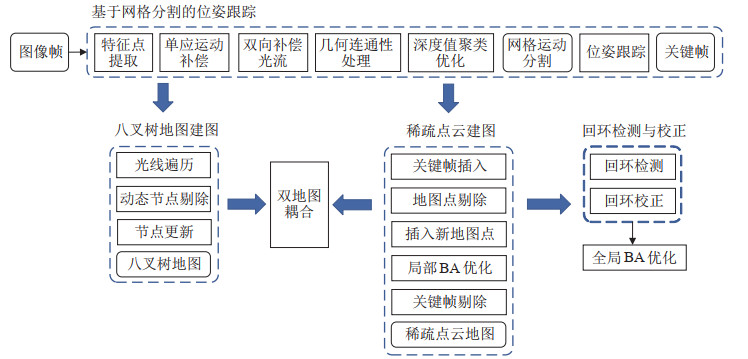
|
图 1 系统流程图 Fig.1 Flow chart of the system |
(1) 基于网格分割的位姿跟踪:提取灰度图像的ORB(oriented brief)特征点[21],引入单应运动补偿方法和根据光流理论设计的双向补偿光流法,结合几何连通性处理方法和深度值聚类方法,形成网格化的运动分割图像,剔除动态特征点,通过最小化重投影误差计算相机位姿。位姿计算完成后,选取部分帧为新的关键帧。
(2) 稀疏点云建图与双地图耦合:根据关键帧还原特征点在3维空间中的位置,在稀疏点云地图中插入地图点。在每个关键帧上,首先根据观测状况剔除低质量的已有地图点,然后利用网格化运动分割图像、结合八叉树地图的双地图耦合技术来筛选并插入新地图点,最后进行局部BA(bundle adjustmen)优化,剔除冗余关键帧。
(3) 八叉树建图:区别于一般的SLAM方法,本文算法基于光线遍历法,根据关键帧上的相机位姿、RGB图像、深度图像、网格化运动分割图像构建场景的静态八叉树地图。
(4) 回环检测与校正:采用ORB-SLAM3中的方法,利用词袋模型进行回环检测。
3 基于网格分割的位姿估计(Pose estimation based on gridding segmentation) 3.1 单应运动补偿与双向补偿光流法单应矩阵描述了2个平面之间的映射关系,单应变换前后点坐标的对应关系由式(1) 计算,
| $ \begin{align} {{\mathit{\boldsymbol{x}}}}_{t+1} & ={{\mathit{\boldsymbol{H}}}}_{t+1, t} {{\mathit{\boldsymbol{x}}}}_{\rm t} \end{align} $ | (1) |
| $ \begin{align} \begin{bmatrix} {x_{t +1 }} \\ {y_{t +1 }} \\ 1 \end{bmatrix} & = \begin{bmatrix} {h_{11}} & {h_{12}} & {h_{13}} \\ {h_{21}} & {h_{22}} & {h_{23}} \\ {h_{31}} & {h_{32}} & {h_{33}} \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \end{align} $ | (2) |
两帧图像的单应矩阵计算依赖两帧之间对应点的匹配。由于存在误匹配和运动特征点等,两帧图像中的特征点对不可能全部满足同一单应变换。因此,使用LMedS(least median of squares)方法确定参与单应矩阵计算的内点,使用Levenberg-Marquardt方法迭代求解单应矩阵。
| $ \begin{align} \mathop{\text{arg min}}\limits_{{{\mathit{\boldsymbol{H}}}}_{t+1, t}} \rm{Median}& \left\{ \left({x_{t+1} -\frac{h_{11} x_{\rm t} +h_{12} y_{\rm t} +h_{13}} {h_{31} x_{\rm t} +h_{32} y_{\rm t} +h_{33}}}\right)^{2} +\right. \\ & \left. \left({y_{t+1} -\frac{h_{21} x_{\rm t} +h_{22} y_{\rm t} +h_{23}} {h_{31} x_{\rm t} +h_{32} y_{\rm t} +h_{33}}}\right)^{2} \right\} \end{align} $ | (3) |
式(3) 将变换后坐标和实际对应坐标之间的像素距离作为误差项,利用LMedS方法进行求解,使得选出点集误差的中值最小化。与RANSAC方法相比,LMedS方法无需手动选择阈值,同时LMedS方法在连续帧序列中得到的单应变换有很好的连续性,较少发生跳变。
两帧之间的对应点信息通过光流法求得。提取第
本文提出了基于光流原理的双向补偿光流法,如图 2所示,根据上文原理对前后两帧
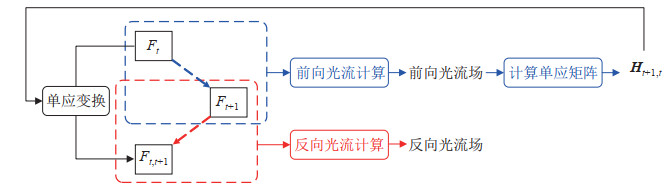
|
图 2 双向补偿光流原理 Fig.2 Principle of the bidirectionally compensated optical flow |
首先讨论补偿图像的含义,将补偿图像与第

|
图 3 补偿图像与后一帧的叠加图像 Fig.3 Superimposed image of the compensated image and the latter frame |
在双向补偿光流过程中记第
| $ \begin{gather} I( x+{\rm d}x, y+{\rm d}y, t+{\rm d}t )=I(x, y, t) \end{gather} $ | (4) |
| $ \begin{gather} I(x_{\rm b}, y_{\rm b}, t)=I({x+{\rm d}x, y+{\rm d}y, t+{\rm d}t}) \end{gather} $ | (5) |
反向光流过程中,进行第
式(6) 为前向光流的光流矢量公式,为方便比较,反向光流的光流矢量定义为该过程中原本光流矢量的相反矢量,如式(7) 所示。
| $ \begin{align} \mathit{\boldsymbol{v}}_{\rm{forward}} & =({\rm d}x, {\rm d}y) \end{align} $ | (6) |
| $ \begin{align} \mathit{\boldsymbol{v}}_{\rm{backward}} & =-(x_{\rm b} -x-{\rm d}x, y_{\rm b} -y-{\rm d}y) \\ & =({\rm d}x+x-x_{\rm b}, {\rm d}y+y-y_{\rm b}) \end{align} $ | (7) |
2个矢量的差值
如图 4光流场显示,和前向光流的结果相比,反向光流计算后静止背景中特征点的移动得到了有效抵消,从而反向光流矢量可以在一定程度上表征一个特征点的运动方向和速度。

|
图 4 前向与反向光流场对比 Fig.4 Comparison of the forward and backward optical flow fields |
从多帧图像序列角度考虑,如图 5所示,为了提高双向补偿光流法的可靠性,在按图 2中的方法计算
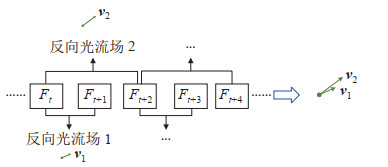
|
图 5 多帧光流对比融合 Fig.5 Comparison and merging of multi-frame optical flow |
图 6(a)为反向光流场1,图 6(b)为反向光流场2。除了一些显著错误的点,反向光流场2的时间跨度更长,运动前景的移动更为显著,按以下条件判断特征点是否做稳定的运动:
| $ \begin{align} \begin{cases} \| {{\mathit{\boldsymbol{v}}}}_{2} \|>\| {{\mathit{\boldsymbol{v}}}}_{1} \|>\delta\\ {{\mathit{\boldsymbol{v}}}}_{1} \cdot {{\mathit{\boldsymbol{v}}}}_{2} >0 \end{cases} \end{align} $ | (8) |

|
图 6 多帧光流场 Fig.6 Multi-frame optical flow |
式(8) 中,
图 7(a)为按3.1节方法得到的动态特征点集合,动点可以表征运动要素所在画面中的位置,但分布较为稀疏,需要进一步得到动态物体在画面中的区域划分。

|
图 7 动态特征点与网格化运动分割 Fig.7 Dynamic feature points and gridding motion segmentation |
将输入图像划分为20
在得到的动态区域结果基础上,基于几何连通性处理孤立区块与被包围区块。如图 8所示,若某动态区块孤立且动态特征点计数少于一定阈值(取为3),则该区块标记为静止。若某静态区块被较多个动态区块包围,则该区块标记为运动。
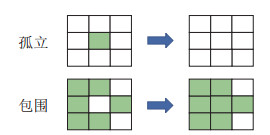
|
图 8 基于连通性的区块处理原理 Fig.8 Schematic of block processing based on connectivity |
经初步处理的网格分割结果已经能够在一定程度上表示画面中的动态区域,但在实际的室内动态场景中还有2种经常出现的情况:(1) 行人在图像中并不会表现出近似刚体的性质。人在走动时,通常各部分的运动情况不一,导致以上的运动分割只覆盖物体的部分区域。(2) 对于弱纹理的运动物体,只在边缘有较强的运动检测响应,初步处理存在不足。因此,按以下步骤对图像的深度值进行K均值聚类,并据此对动态区域进行进一步优化。
将深度图像降采样至20
| $ \begin{align} P({x_{i}})=\frac{D^{2}({x_{i}})}{\sum \limits_i {D^{2}({x_{i}})}} \end{align} $ | (9) |
K-Means

|
图 9 深度值聚类结果与动态区域优化结果 Fig.9 Depth clustering result and dynamic region optimization result |
如图 10所示,参照深度值聚类结果扩展和填充动态区域。若动态区域中的一个连通区域与某聚类簇内的一个连通区域重合度高于阈值
| $ \begin{align} r=\frac{s}{s_{1} +s_{2} -s} \end{align} $ | (10) |

|
图 10 基于聚类的区块优化原理 Fig.10 Schematic of block optimization based on clustering |
其中,
由于结合3帧连续图像进行运动分割,算法每隔一帧得出一次运动分割。因为两帧之间时间较短、运动量极小,所以没有分割的帧可以继承前一帧的运动分割结果。
3.4 消除动态影响的位姿估计结合RGB图像和深度图像得出动态区域分割结果后,根据网格分割结果对当前帧中的特征点的运动性质作出判断,落在动态区域内的特征点为动态特征点,记为集合
| $ \begin{align} \mathit{\boldsymbol{T}}_{\rm{cw}} =\text{arg min} \sum _{i\in \chi_{\rm s}} \rho \left({\| {\mathit{\boldsymbol{x}}_{i} -\boldsymbol \pi ( \mathit{\boldsymbol{T}}_{\rm{cw}} \mathit{\boldsymbol{P}}_{i} )} \|_{\mathit{\boldsymbol{\varSigma}}}^{2}}\right) \end{align} $ | (11) |
其中:
| $ \begin{align} \boldsymbol \pi \left(\begin{bmatrix} X \\ Y \\ Z \end{bmatrix}\right) & =\begin{bmatrix} f_{ x} \dfrac{X}{Z}+c_{ x} \\[6pt] f_{ y} \dfrac{Y}{Z}+c_{ y} \end{bmatrix} \end{align} $ | (12) |
| $ \begin{align} \mathit{\boldsymbol{\varSigma}} & =n\cdot \mathit{\boldsymbol{E}} \end{align} $ | (13) |
利用高斯—牛顿方法对最小化重投影误差问题进行求解,优化得到相机的位姿估计。
4 双地图构建与耦合(Construction and coupling of the dual maps) 4.1 基于光线遍历法的八叉树地图构建本文算法在跟踪相机位姿的同时会建立场景稀疏点云地图进行定位,但是稀疏点云地图不足以充分描述场景细节,也不能用于导航和路径规划。系统设计了八叉树地图模块,基于光线遍历法,接收了关键帧的相机位姿、RGB图像、深度图像、网格分割图像信息,建立和更新了场景的静态地图。
八叉树地图将3维空间划分为立方体节点,其中叶子节点通过占据和置空2种状态来表示该位置是否存在障碍物。为了降低计算量、减少冗余,更新地图时对图像进行1/4降采样,在行和列上每4个像素选取1个像素进行更新。将动态区域掩模信息应用到八叉树地图的建立当中,算法只根据静态区域内的图像信息更新八叉树地图,不在八叉树地图当中插入动态区域对应节点,这样可以一定程度上避免动态物体的信息被记录到地图当中。
更新地图时采用一种光线遍历方法,如图 11所示,从相机光心

|
图 11 光线遍历法构建地图 Fig.11 Mapping with ray traversal method |
(1) 光线穿过若干数量的被占据节点后将路径上所有被占据节点置为空,将末端节点置为占据。
(2) 光线未穿过被占据节点,但末端落在被占据节点上,则不更新地图。
(3) 光线未穿过被占据节点,且末端不落在被占据节点上,则将末端节点置为占据。
八叉树中的光线遍历计算通过3维数值微分算法实现。动态掩模和光线遍历更新消除了地图中由于同一动态物体运动到不同位置时的信息被多次记录导致的“残影”。
4.2 稀疏点云地图与静态八叉树地图耦合算法在关键帧上会通过RGB-D相机的深度测量结果还原部分ORB特征点在3维空间中的坐标,并将其加入到稀疏点云地图中用于特征匹配和位姿计算,如图 12所示。属于动态物体的地图点被加入地图后,将导致在该位置上后期进行位姿跟踪时会产生错误匹配,影响位姿估计精度。为了避免这种现象,使用运动分割生成的动态区域掩模帮助稀疏点云地图筛选一部分动态地图点。除此之外,还将采用一种基于八叉树地图光线遍历法的方法进一步剔除一部分动态地图点,实现2种地图之间的耦合,通过先前对场景3维结构的认知来指导稀疏点云建图。

|
图 12 剔除动态点的稀疏点云 Fig.12 Sparse point cloud after removing dynamic points |
根据特征点的2维坐标可以在深度图中查询对应的深度值,记为
| $ \begin{align} {{\mathit{\boldsymbol{P}}}}_{\rm c} =z_{\rm c} {{\mathit{\boldsymbol{K}}}}^{-1}{{\mathit{\boldsymbol{P}}}} \end{align} $ | (14) |
根据相机位姿变换
| $ \begin{align} {{\mathit{\boldsymbol{P}}}}_{\rm w} ={{\mathit{\boldsymbol{T}}}}_{\rm{cw}}^{-1}{{\mathit{\boldsymbol{P}}}}_{\rm c} ={{\mathit{\boldsymbol{R}}}}^{-1}({{{\mathit{\boldsymbol{P}}}}_{\rm c} -{{\mathit{\boldsymbol{t}}}}}) \end{align} $ | (15) |
其中,相机位姿变换
| $ \begin{align} {{\mathit{\boldsymbol{P}}}}_{\rm{cam}} ={{\mathit{\boldsymbol{t}}}} =[{x_{\rm{cam}}} \; \; {y_{\rm{cam}}} \; \; {z_{\rm{cam}}} ]^{\rm T} \end{align} $ | (16) |
在八叉树地图中进行从
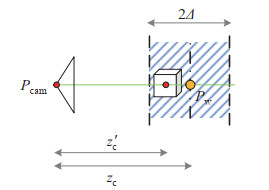
|
图 13 光线遍历法筛选稀疏地图点 Fig.13 The sparse map points filtered by ray traversal method |
RGB-D相机在测量较远物体的深度时误差较大,因此只对4 m内的地图点作深度值检查。图 13中,如果
| $ \begin{align} \begin{cases} z_{\rm c} <4 \\ z_{\rm c}' >z_{\rm c} +\varDelta \\ z_{\rm c}' <z_{\rm c} -\varDelta \end{cases} \end{align} $ | (17) |
其中
| $ \begin{align} z_{\rm k}^{-1} = {\frac{m}{fb}}{d}'+ {z_{0}^{-1} +\frac{n}{fb}} \end{align} $ | (18) |
Kinect v1相机误差主要来源于视差量化,假设
| $ \begin{align} \sigma_{\rm z}^{2} = {\frac{\partial z}{\partial d}}\sigma_{\rm d'}^{2} \end{align} $ | (19) |
简化得到深度值的标准差:
| $ \begin{align} \sigma_{\rm z} = {\frac{m}{fb}}z^{2}\sigma_{\rm d'} \end{align} $ | (20) |
由式(20) 可知,深度值测量的随机误差与物体实际深度的平方成正比。Zennaro等[24]测量了各个距离上Kinect v1相机的测量精度,误差与深度成二次函数关系,印证了式(20) 的误差模型。将Kinect v1相机测量误差
| $ \begin{align} \varDelta_{\rm z} =\beta_{1} z^{2}+\beta_{2} z+\beta_{3} \end{align} $ | (21) |
通过最小二乘法拟合文中的测量结果得到
| $ \begin{align} \varDelta =\varDelta_{\rm z} +\varDelta_{\rm t} +\varDelta_{\rm o} \end{align} $ | (22) |
本文提出的运动分割方法基于ORB特征点与稀疏光流计算,对纹理和垂直于深度方向的运动比较敏感。光线遍历方法对低纹理和沿深度方向运动的物体也具有很好的敏感性。基于八叉树光线遍历的双地图耦合方法对基于运动分割的地图点筛选形成了很好的补充。
5 实验与分析(Experiment and analysis)本文实验使用的计算机硬件参数为:AMD Ryzen 5 2600X CPU,主频3.6 GHz,16 GB内存,不使用GPU加速。软件环境为Ubuntu 16.04系统及ROS(robot operating system)Kinetic框架。通过公开数据集实验验证算法在动态场景中的定位精度,通过移动机器人实验验证算法在实际机器人平台上工作时运动分割、抵抗运动干扰、在线建图的多种能力以及运行效率。
5.1 TUM RGB-D数据集定位精度与时效实验TUM RGB-D数据集是由慕尼黑工业大学发布的SLAM评测数据集,主要针对纹理丰富的办公室场景,包含手持RGB-D相机拍摄的图像序列及使用高精度运动捕捉设备获取的相机轨迹真值。图像帧率30帧/s,分辨率为640
为了评价SLAM系统定位的精确性,使用绝对轨迹误差(absolute trajectory error,ATE)和相对位姿误差(relative pose error,RPE)作为评价指标。ATE表示每一时刻位姿估计与位姿真值之间的绝对误差,反映了轨迹的全局一致性。由于在一个图像序列上的不同时刻可以计算得到多个ATE值,统计ATE的均方根误差(root mean squared error,RMSE)来评价SLAM位姿估计的精度。RPE每隔一段相同时间(取为1帧对应的时间)分别计算位姿估计和位姿真值的变化量,然后计算这2个变化量的差值,该差值能反映定位的漂移情况。
为说明双地图耦合方法的有效性,分别在关闭和开启双地图耦合的情况下运行算法。关闭双地图耦合时算法无法通过对场景3维结构的认知筛选动态地图点,仅能通过网格化运动分割进行筛选。
表 1列出了各种算法在8个序列下运行得到的绝对误差的RMSE值,其中组别“本文算法-A”为关闭双地图耦合的本文算法,“本文算法-B”为开启双地图耦合的本文算法。同时,选择4种动态SLAM方案进行对比,分别采用了帧差法[6]、稠密光流法[3]、深度学习方法[13]以及几何与运动约束法[10],前3种方法都能提供像素级的动态分割。
|
|
表 1 TUM数据集上的绝对轨迹误差统计值 Tab. 1 Statistic values of absolute trajectory error on TUM dataset |
可以看出,本文算法在低动态的“sitting”序列中与ORB-SLAM3算法有相似的定位精度,但在所有的高动态“walking”序列中,相较ORB-SLAM3算法其定位精度都有较大的提升,ORB-SLAM3算法在多个高动态场景都受到了动态物体的严重干扰,发生了位姿漂移,产生了很高的定位误差。进一步地,本文算法在不进行双地图耦合的情况下,已经能够在大部分场景中取得相对可靠的定位结果。但开启八叉树建图和基于八叉树地图的地图点筛选之后,高动态“walking”序列中算法的定位精度均有一定程度的提高,与无法适应动态场景的ORB-SLAM3算法相比,本文算法在这些序列上的定位精度误差平均下降了91.5%。
对比“本文算法-B”与其他几种动态SLAM方案,所有方案都可以有效抵抗动态场景的干扰。除去相机激烈转动导致大部分算法表现不佳的“walking_rpy”序列,本文算法的定位精度整体优于帧差法与稠密光流法,而与几何与运动约束法、DS-SLAM算法在同一数量级上,在“walking_xyz”序列上甚至具有最低的绝对轨迹误差。但是其中几何与运动约束法基于稀疏地图点滤除动态特征,对图像的动态物体区域没有感知,且不提供在线的稠密建图。本文算法的精度与DS-SLAM算法接近,其中在“rpy”“xyz”序列上更高。说明本文算法在动态场景中具有良好的定位精度。
特别地,在“walking_xyz”序列中,开关八叉树遍历的地图点筛选方法前后定位精度有较大的提升,如图 14所示。图 14(a)为ORB-SLAM3算法、关闭双地图耦合的本文算法(本文算法-A)、开启双地图耦合的本文算法(本文算法-B)在该序列上的ATE图像,将对应时间戳上的相机坐标误差用红色连线表示。图 14(b)为这3种算法对应的RPE曲线。由图 14可知,未开启双地图耦合时,轨迹与真值基本吻合但轨迹起点处存在较大的漂移,反映在RPE曲线中RPE值在前3 s较大,3 s之后减小。开启双地图耦合后,轨迹的吻合程度进一步提升,对应的RPE值整体降低到更低水平。
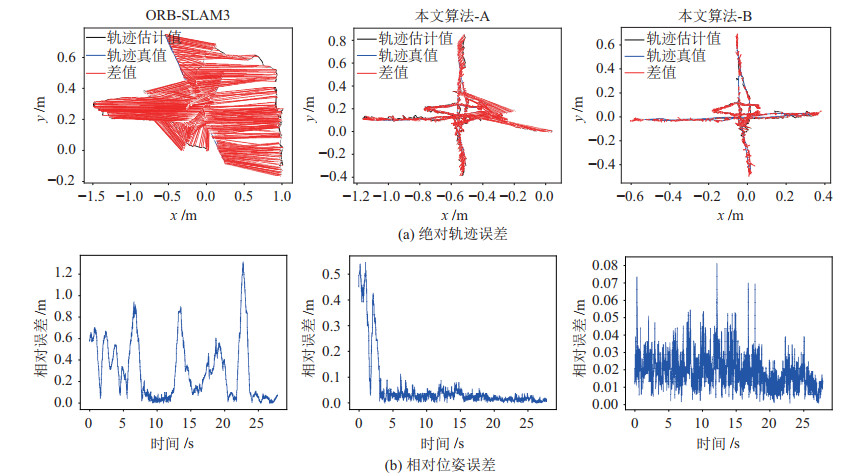
|
图 14 fr3/walking_xyz序列上的绝对轨迹误差与相对位姿误差 Fig.14 Absolute trajectory error and relative pose error on fr3/walking_xyz sequence |
分析该序列的特点可以发现,该序列的前几秒画面中有一显著的人物远离镜头运动。本文中的运动分割方法基于稀疏光流,依赖2维的特征信息,对于深度方向运动的敏感性较低,单纯的运动分割或将不足以处理这类运动目标。而基于八叉树地图的地图点筛选方法依赖深度值变化,2种方法互相补充,能够应对更多的情况,因此能够进一步提高动态地图点的滤除效果,提升定位精度。
5.1.2 运行效率分析为了验证本文算法的快速性,对算法的运行效率进行分析,并与ORB-SLAM3算法、DS-SLAM算法进行对比。对于多线程架构的SLAM算法,实时跟踪相机位姿的跟踪线程的计算效率能够反映算法的整体运行效率。
对照实验在fr3/walking_xyz序列上进行,统计跟踪线程在每一帧上消耗的时间,如图 15所示。3种算法的耗时呈现显著带状分布,ORB-SLAM3算法与本文算法的耗时都集中在30~60 ms区间,DS-SLAM算法耗时集中在70~100 ms区间。本文算法耗时显著低于DS-SLAM算法,与ORB-SLAM3算法在同一水平,但ORB-SLAM3算法只能用于静态场景,不适用于动态场景。
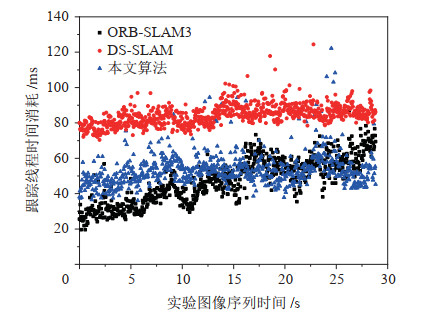
|
图 15 fr3/walking_xyz序列上的跟踪线程耗时 Fig.15 Time cost of tracking thread on fr3/walking_xyz sequence |
计算算法的平均耗时,由表 2可知,DS-SLAM算法耗时相对ORB-SLAM3算法超出78.07%,而本文算法相对ORB-SLAM3算法仅引入12.90% 的额外耗时。
|
|
表 2 fr3/walking_xyz序列上的跟踪线程平均耗时与相对ORB-SLAM3算法的耗时增幅 Tab. 2 Average time cost of the tracking thread and increase relative to ORB-SLAM3 method on fr3/walking_xyz sequence |
DS-SLAM算法的耗时主要来源于图像分割网络,且图像分割需要GPU硬件支持。本文采用的基于稀疏光流法设计的双向补偿光流法可以快速而有效地识别运动特征,因此具有很高的计算效率。
5.2 实际动态场景分割与建图实验为了验证算法,在实际的移动机器人平台上进行室内动态场景定位、建图的可行性分析,使用TurtleBot2移动机器人平台进行实验,如图 16所示。TurtleBot2搭载Kinect v1相机,在实验室动态场景中按照设定的路径移动,移动的同时运行本文SLAM算法进行实时的定位和在线八叉树建图。
|
图 16 TurtleBot2移动机器人与实验平台 Fig.16 TurtleBot2 mobile robot and experiment platform |
所设定的路径为以0.2 m/s的速度直线行驶1.75 m,向左旋转90
图 17为ORB-SLAM3算法与本文算法的定位轨迹,以及TurtleBot2机器人的设定运动轨迹。当走动的人进入相机视野时,ORB-SLAM3算法的轨迹随着人的运动发生了较大的漂移,而本文算法的轨迹未受到运动物体的显著影响。
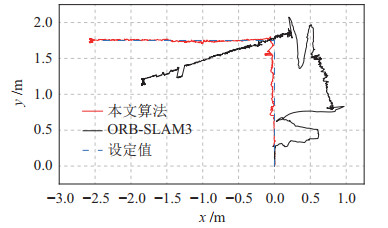
|
图 17 机器人行动轨迹 Fig.17 Robot motion trajectory |
在实验的图像序列中截取包含和不包含运动物体的画面,如图 18所示。下方为算法运动分割得到的动态区域掩模图像,上方为成功跟踪的特征点,其中红色为动态特征点,绿色为静态特征点。由图 18可以发现,动态区域掩模基本覆盖了画面中运动的人物,能够粗略分割物体轮廓,也能很好地区分特征点,较少将静态特征点判为动态的噪声,误判程度在合理范围内。

|
图 18 运动分割 Fig.18 Motion segmentation |
如图 19所示,由于位姿估计未受动态物体干扰,地图未出现扭曲,房间结构清晰,与实际环境一致。所得到的八叉树地图分辨率高,包含节点的颜色信息,还原了场景的原貌。图 19(b)中地图记录了多个关键帧上运动物体的信息,形成了“残影”现象。图 19(c)中地图根据运动分割和后续的观察更新有效地剔除了“残影”,仅包含场景中的静态要素,适用于移动机器人导航等。

|
图 19 八叉树建图结果 Fig.19 Octree mapping result |
为进一步验证八叉树建图在大场景中建图的稳定性,先后对大楼中的房间、走廊1、门厅、走廊2场景进行建图,如图 20所示。图 20为大场景地图与其中各个场景的八叉树地图。其中走廊宽度2.40 m,高度2.80 m,走廊1长度29.25 m,走廊2长度15.25 m。实验结果表明,实测结果与八叉树地图中数据非常吻合,房间场景中人物未产生重影,地图连续、完整,对场景结构还原到位,体现了本文算法在大场景中建图具有较强的稳定性。

|
图 20 大场景八叉树建图结果 Fig.20 Octree mapping result in big scenes |
提出了一种室内动态环境下基于网格分割与双地图耦合的RGB-D SLAM算法。算法首先引入单应运动补偿与根据光流理论设计的双向补偿光流法来发现图像中的动态特征点。将动态特征点的位置反映到网格图像中并根据几何连通性和深度值聚类结果优化分割结果,得到图像的网格化运动分割。通过提出的双向补偿光流法和网格化处理保障了运动分割的计算效率。之后利用静态区域中的特征点最小化重投影误差,得到相机的准确位姿估计。基于位姿估计,使用网格分割和光线遍历方法构建场景的静态八叉树地图,使地图中不包含动态物体的“残影”。此外,提出双地图耦合方法,同时利用网格化运动分割图像和八叉树地图光线遍历的方法剔除稀疏点云地图中的动态地图点,提升位姿估计精度。分别在TUM数据集和实际场景中对本文算法进行了验证。相比ORB-SLAM3算法,本文算法在动态场景中的定位进度和鲁棒性有了很大提升,相比其他适用于动态场景的SLAM算法,本文算法执行效率高,定位精度高,在大场景中建图稳定性强。
在下一步的工作当中,将讨论在室内动态环境下RGB-D SLAM中使用多目标追踪算法对动态物体进行持续跟踪。同时还将融入IMU(惯性测量单元)进一步提高SLAM系统的精度和鲁棒性。
| [1] |
Rosen D M, Doherty K J, Espinoza A T, et al. Advances in inference and representation for simultaneous localization and mapping[J]. Annual Review of Control, Robotics, and Autonomous Systems, 2021, 4: 215-242. DOI:10.1146/annurev-control-072720-082553 |
| [2] |
Saputra M R U, Markham A, Trigoni N. Visual SLAM and structure from motion in dynamic environments: A survey[J]. ACM Computing Surveys, 2018, 51(2): 1-36. |
| [3] |
Sun Y X, Liu M, Meng M Q H. Motion removal for reliable RGB-D SLAM in dynamic environments[J]. Robotics and Autonomous Systems, 2018, 108: 115-128. DOI:10.1016/j.robot.2018.07.002 |
| [4] |
Wang Y B, Huang S D. Towards dense moving object segmentation based robust dense RGB-D SLAM in dynamic scenarios[C]//13th International Conference on Control, Automation, Robotics&Vision. Piscataway, USA: IEEE, 2014. DOI: 10.1109/ICARCV.2014.7064596.
|
| [5] |
Lee S, Son C Y, Kim H J. Robust real-time RGB-D visual odometry in dynamic environments via rigid motion model[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2019. DOI: 10.1109/IROS40897.2019.8968208.
|
| [6] |
Sun Y X, Liu M, Meng M Q H. Improving RGB-D SLAM in dynamic environments: A motion removal approach[J]. Robotics and Autonomous Systems, 2017, 89: 110-122. DOI:10.1016/j.robot.2016.11.012 |
| [7] |
高成强, 张云洲, 王晓哲, 等. 面向室内动态环境的半直接法RGB-D SLAM算法[J]. 机器人, 2019, 41(3): 372-383. Gao C Q, Zhang Y Z, Wang X Z, et al. Semi-direct RGB-D SLAM algorithm for dynamic indoor environments[J]. Robot, 2019, 41(3): 372-383. |
| [8] |
魏彤, 李绪. 动态环境下基于动态区域剔除的双目视觉SLAM算法[J]. 机器人, 2020, 42(3): 336-345. Wei T, Li X. Binocular vision SLAM algorithm based on dynamic region elimination in dynamic environment[J]. Robot, 2020, 42(3): 336-345. |
| [9] |
张慧娟, 方灶军, 杨桂林. 动态环境下基于线特征的RGBD视觉里程计[J]. 机器人, 2019, 41(1): 75-82. Zhang H J, Fang Z J, Yang G L. RGB-D visual odometry in dynamic environments using line features[J]. Robot, 2019, 41(1): 75-82. |
| [10] |
艾青林, 刘刚江, 徐巧宁. 动态环境下基于改进几何与运动约束的机器人RGB-D SLAM算法[J]. 机器人, 2020, 43(2): 167-176. Ai Q L, Liu G J, Xu Q N. An RGB-D SLAM algorithm for robot based on the improved geometric and motion constraints in dynamic environment[J]. Robot, 2020, 43(2): 167-176. |
| [11] |
Bescos B, Facil J M, Civera J, et al. DynaSLAM: Tracking, mapping, and inpainting in dynamic scenes[J]. IEEE Robotics and Automation Letters, 2018, 3(4): 4076-4083. DOI:10.1109/LRA.2018.2860039 |
| [12] |
He K M, Gkioxari G, Dollár P, et al. Mask R-CNN[C]//IEEE International Conference on Computer Vision. Piscataway, USA: IEEE, 2017. DOI: 10.1109/ICCV.2017.322.
|
| [13] |
Yu C, Liu Z X, Liu X J, et al. DS-SLAM: A semantic visual SLAM towards dynamic environments[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2018. DOI: 10.1109/IROS.2018.8593691.
|
| [14] |
Badrinarayanan V, Kendall A, Cipolla R. SegNet: A deep convolutional encoder-decoder architecture for image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(12): 2481-2495. DOI:10.1109/TPAMI.2016.2644615 |
| [15] |
Zhong F W, Wang S, Zhang Z Q, et al. Detect-SLAM: Making object detection and SLAM mutually beneficial[C]//IEEE Winter Conference on Applications of Computer Vision. Piscataway, USA: IEEE, 2018. DOI: 10.1109/WACV.2018.00115.
|
| [16] |
Rother C, Kolmogorov V, Blake A. "GrabCut": Interactive foreground extraction using iterated graph cuts[J]. ACM Transactions on Graphics, 2004, 23(3): 309-314. DOI:10.1145/1015706.1015720 |
| [17] |
姚二亮, 张合新, 宋海涛, 等. 基于语义信息和边缘一致性的鲁棒SLAM算法[J]. 机器人, 2019, 41(6): 751-760. Yao E L, Zhang H X, Song H T, et al. Robust SLAM algorithm based on semantic information and edge consistency[J]. Robot, 2019, 41(6): 751-760. |
| [18] |
Redmon J, Farhadi A. YOLOv3: An incremental improvement[DB/OL]. (2018-04-08)[2020-03-21]. https://arxiv.org/abs/1804.02767v1.
|
| [19] |
Liu H J, Liu G L, Tian G H, et al. Visual SLAM based on dynamic object removal[C]//IEEE International Conference on Robotics and Biomimetics. Piscataway, USA: IEEE, 2019. DOI: 10.1109/ROBIO49542.2019.8961397.
|
| [20] |
Campos C, Elvira R, Rodríguez J J G, et al. ORB-SLAM3:An accurate open-source library for visual, visual-inertial and multi-map SLAM[J]. IEEE Transactions on Robotics, 2021, 37(6): 1874-1890. DOI:10.1109/TRO.2021.3075644 |
| [21] |
Rublee E, Rabaud V, Konolige K, et al. ORB: An efficient alternative to SIFT or SURF[C]//International Conference on Computer Vision. Piscataway, USA: IEEE, 2011. DOI: 10.1109/ICCV.2011.6126544.
|
| [22] |
Arthur D, Vassilvitskii S. K-means++: The advantages of careful seeding[C]//8th Annual ACM-SIAM Symposium on Discrete Algorithms. New York, USA: ACM, 2007: 1027-1035.
|
| [23] |
Khoshelham K, Elberink S O. Accuracy and resolution of Kinect depth data for indoor mapping applications[J]. Sensors, 2012, 12(2): 1437-1454. DOI:10.3390/s120201437 |
| [24] |
Zennaro S, Munaro M, Milani S, et al. Performance evaluation of the 1st and 2nd generation Kinect for multimedia applications[C]//IEEE International Conference on Multimedia and Expo. Piscataway, USA: IEEE, 2015. DOI: 10.1109/ICME.2015.7177380.
|
 2022, Vol. 44
2022, Vol. 44


