1 引言（Introduction）

多移动机器人系统凭借其良好的灵活性、可扩展性等特点被广泛应用在各种领域^[1]。在工业领域，通过控制多个机器人保持不同的队形以适应不同形状货物的搬运；在军事领域，多机器人系统被广泛应用于军事边防编队巡逻、地理资源勘测、侦察救援中。在多机器人系统问题中编队控制一直是研究的核心问题，编队控制不仅要实现多机器人系统的运动控制，还要利用编队算法使其保持期望的队形^[2]。对于机器人编队算法的研究已经开展了数十年，产生了以领导者—跟随者、虚拟结构法、基于行为法和人工势场法为代表的一系列成熟有效的编队策略^[3-6]。

但是受限于当前算法和机器人的智能程度，实现全自主机器人编队控制有很大的挑战性和不确定性^[7]。鉴于人类具备适应新环境并作出合理决策的能力，可以把人类操作员的控制意识集成到编队系统中^[8]。基于力反馈手控器的双边遥操作控制模式将人的认知以及决策能力引入到机器人编队系统的控制中^[9-10]。适当的力反馈可以帮助操作员充分理解机器人编队与周围环境的交互信息^[11-12]，例如主从跟踪误差^[13]、编队与障碍物之间的距离^[14]。但是使用力反馈手控器与机器人编队进行交互时，还存在一些不可避免的问题。文[13]研究了操作员与一组飞行器的交互，但是仅利用力反馈手控器末端关节的位置来控制飞行器系统的平均速度。文[15]中操作员把力反馈手控器末端关节的$ x $轴和$ y $轴的位置分别映射为机器人编队在$ x $轴和$ y $轴方向的速度，把$ z $轴的位置映射为编队队形大小的控制命令。由于受力反馈手控器的机械限制，操作人员向从端机器人编队发布遥操作命令时会受到一定程度的约束。文[16]提出了一种队形平滑切换方法，在编队系统切换队形以适应不同环境的过程中引入平滑过渡方法，为操作员提供稳定的反馈力。文[17]提出了具有时变拓扑的机器人编队双边遥操作系统，手控器控制编队的速度，接收到的反馈力表示从端编队系统对主端发布命令的跟踪情况。但是在一些复杂的任务场景里，如果改变编队系统的队形、尺寸和运动方向，基于力反馈手控器的单一输入模式会使控制操作变得复杂、控制效率降低。文[9]研究了操作人员利用双边遥操作协助机器人编队完成任务，把手控器末端关节在其中一个轴上的位置信息映射为队形改变命令。由于手控器位置信息和队形改变命令两者之间的高度不匹配，因此需要操作员事先记住两者的映射关系。所以当利用手控器发布一些抽象的命令时，基于手控器的手动输入是非常不直观的。

手控器提供的力反馈可减轻人机分离造成的感知缺失、提升操控沉浸感，但作为单模态输入与编队系统交互时，存在交互不直观、操作员负荷沉重等问题。由于视线信号可以用来识别操作员的意图、摆脱对肢体动作的要求、消除由于身体不便或者环境约束造成的输入障碍^[18]，利用视线信号作为新的输入模态来控制机器人也逐渐引起关注^[19-20]。英国诺丁汉特伦特大学提出一种基于视线跟踪的遥操作控制系统^[21]，使用视线跟踪算法计算操作员注视点在交互界面上的坐标，并将其转换为移动机器人的控制命令。荷兰特温特大学将视线信号与手控器信号相结合，开发了一种人机交互技术，视线信号被用来确定触摸点，操作员利用手控器进行触摸时可以感受到反馈力^[22]。目前利用视线信号遥操作控制的对象主要是单一智能体，针对多智能体的研究极少。本文将视线信号作为手控器输入模态的有力补充而非替代，不仅可以保留手控器输入模态的灵活性和可靠性，还可以增加对编队控制的自由度，提高与编队系统交互的直观性。

目前在双边遥操作机器人编队控制中，从端编队存在成员之间约束力不够、编队灵活性差等缺点。文[23]提出了一种基于分散估计控制和双边遥操作的机器人编队系统，编队成员之间通过无向连接图交换信息，该方案虽然有良好的可扩展性，但成员之间约束力不够。文[24]提出了一种基于遥操作和虚拟刚体的四旋翼飞行器协同避障方法，把四旋翼编队看成一个虚拟刚体，在四旋翼与障碍物之间建立矢量场以实现外部避障，在编队内部建立矢量场以实现内部避碰。国外针对机器人编队控制的研究开展较早，国内在编队控制领域的研究开展较晚，成果也相对较少。如文[25]采用虚拟结构法对无人机编队控制问题进行分析，实现了虚拟刚体坐标系下不同队形的切换，但其灵活性一般。

针对手控器单模态输入的移动机器人编队控制面临的上述问题，本文提出一种基于手眼双模态人机接口的编队共享控制方法。主端双模态人机接口的输入信号有操作员的手部输入信号和视线跟踪信号，两种信号被映射为不同的遥操作命令。从端编队基于虚拟结构和人工势场法构建，增加了编队的灵活性和约束力。遥操作控制器采用一种基于共享控制的框架实现。具体实现方式是操作员通过双模态人机接口发布遥操作命令，编队行进动作和队形切换动作由操作员远程控制完成，而外部避障、队形保持和内部避碰动作由从端编队自主完成。设计实验验证该方法的可行性，并通过对比实验证明该方法能提高控制效率、减轻操作人员负荷。

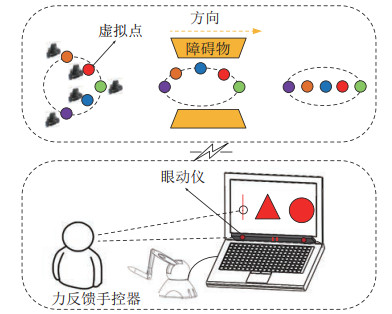
2 系统设计（System design）

图 1所示是基于双模态人机接口的编队系统示意图。主端包括操作人员、眼动仪、力反馈手控器和人机交互界面，从端包括由多个移动机器人组成的编队系统、监控摄像头和周围环境。主、从端之间通过局域网实现双向通信，操作人员控制手控器，将6自由度操作杆的位置和角度信息转换成编队运动的速度和方向命令。与此同时，眼动仪捕捉到的视线信号经过处理转换成编队的队形切换命令。在从端环境中，机器人编队被看成一个由虚拟点构成的虚拟刚体结构，编队中的每个成员被抽象为一个虚拟的点并跟随虚拟点的运动轨迹。在主端，操作人员可以通过人机交互界面看到实时的任务场景，力反馈手控器传递的临场力觉感能反映主端发布速度与从端实际速度的不匹配程度。

2.1 主端眼动仪命令函数设计

视线跟踪作为一种新型的人机交互方式，摆脱了对操作员肢体动作的束缚，能够很大程度上减轻操作人员的负荷。设计如图 1所示的人机交互界面，可以根据工作环境预先定义所需的编队形状图案。眼动仪根据操作者在人机交互界面上注视点的位置和注视持续时间来捕获操作者的意图，被操作人员视线注视的图案以固定的频率闪烁，告知操作人员主端的眼动仪正在把视线信号转换为队形切换命令，从端机器人编队可以根据该命令调整为相应的队形。眼动仪的命令函数可以描述为

$ \begin{equation} \begin{cases} {\mathit{\boldsymbol{X}}}_{\rm e} ={\mathit{\boldsymbol{f}}}_{\rm e} ({\mathit{\boldsymbol{q}}}_{\rm{ep}}, {\mathit{\boldsymbol{q}}}_{\rm{et}}) \\ {{\mathit{\boldsymbol{f}}}}_{\rm e} ({\mathit{\boldsymbol{q}}}_{\rm{ep}}, {\mathit{\boldsymbol{q}}}_{\rm{et}})=[{f_{{\rm e}1} (q_{{\rm{ep}}1}, q_{{\rm{et}}1}), \cdots, f_{{\rm e}m} (q_{{\rm{ep}}m}, q_{{\rm{et}}m})}]^{\rm T} \end{cases} \end{equation} $

(1)

$ {\mathit{\boldsymbol{X}}}_{\rm e} \in \mathbb{R}^{\rm l} $代表人工命令函数向量，$ f_{{\rm e}i} (q_{{\rm{ep}}i}, q_{{\rm{et}}i}) $（$ i=1, \cdots, m $）表示命令函数，由操作人员的注视点$ q_{{\rm{ep}}i} $和注视持续时间$ q_{{\rm{et}}i} $决定。$ m $表示眼动仪产生信号命令的个数，$ m=1 $时，眼动仪发布命令$ X_{{\rm e}1} $控制编队的队形切换。当$ m=2 $时，产生2种控制命令$ X_{{\rm e}1} $和$ X_{{\rm e}2} $，分别控制编队的队形切换和编队运动的目标位置。在本文中，假设$ m=1 $，则眼动仪的命令函数为

$ \begin{align} S_{\rm e} =f_{\rm{ep}} (q_{\rm{ep}})f_{\rm{et}} (q_{\rm{et}}) \end{align} $

(2)

$ S_{\rm e} $表示操作人员的意图即操作人员期望的编队形状。$ f_{\rm{ep}}, f_{\rm{et}} $分别和$ q_{\rm{ep}}, q_{\rm{et}} $对应，其对应关系为

$ \begin{equation} f_{\rm{ep}} (q_{\rm{ep}})=j\; (q_{\rm{ep}} =\varOmega_{j}), \; \; f_{\rm{et}} (q_{\rm{et}})= \begin{cases} 0, & q_{\rm{et}} \leqslant 1\:{\rm s} \\ 1, & q_{\rm{et}} >1\:{\rm s} \end{cases} \end{equation} $

(3)

其中，$ \varOmega_{j} $表示眼动仪注视的位置，$ j $表示图 1中视线焦点区域选择的图案，设置1 s的间隔时间是为了防止操作人员视线漂移造成误操作。

2.2 从端编队系统虚拟结构设计

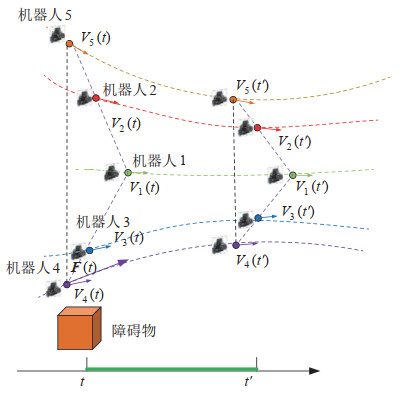
如图 2所示，从端编队系统被视为一个虚拟结构。虚拟结构由$ n $个虚拟点组成，其广义坐标可表示为$ {\mathit{\boldsymbol{q}}}_{\rm s} ={\rm{diag}} [{\mathit{\boldsymbol{q}}}_{{{\rm s}1}}^{\rm T}, \cdots , {\mathit{\boldsymbol{q}}}_{{{\rm s}n}}^{\rm T}] $，虚拟结构的任务空间可表示为

$ \begin{align} \begin{cases} {\mathit{\boldsymbol{X}}}_{\rm s} =\mathit{\boldsymbol{f}}_{\rm s} ({\mathit{\boldsymbol{q}}}_{\rm s}) \\ \dot{\mathit{\boldsymbol{X}}}_{\rm s} =\mathit{\boldsymbol{J}}_{\rm s} ({\mathit{\boldsymbol{q}}}_{\rm s})\dot{\mathit{\boldsymbol{q}}}_{\rm s} \end{cases} \end{align} $

(4)

$ {\mathit{\boldsymbol{X}}}_{\rm s} ({\mathit{\boldsymbol{q}}}_{\rm s})\in \mathbb{R}^{m+l} $表示主端向虚拟结构发布的遥操作任务，任务的总数为$ m+l $，其中$ l $个任务由力反馈手控器发布，眼动仪发布的任务个数是$ m $。

在微观层面上，每个编队成员都被抽象为虚拟点，图中灰色虚线表示虚拟点维持的编队形状。$ t $时刻虚拟结构维持一个三角形队形，到$ t^{\prime} $时刻，虚拟结构缩小尺寸。每个编队成员遵循其虚拟点的运动轨迹，并使用跟踪算法使跟踪误差降到最低^[26]。机器人的当前位置信息可以采用航位推算法计算出来，首先作离散化处理。图 3所示为航位推算法的示意图，已知初始位姿$ (x_{0}, y_{0}, \theta_{0}) $，则$ k $时刻机器人的位姿为

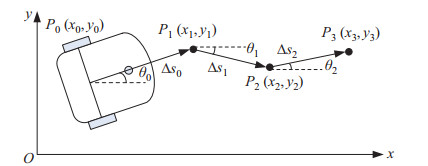
$ \begin{align} \begin{cases} x_{k} =x_{0} +\sum\limits_{i=1}^k {\Delta s_{i-1} \cos \theta_{i-1}} \\ y_{k} =y_{0} +\sum\limits_{i=1}^k {\Delta s_{i-1} \sin \theta_{i-1}} \\ \theta_{k} =\theta_{k-1} +\Delta \theta_{k} \end{cases} \end{align} $

(5)

3 共享控制框架（Shared control framework）

本文提出的共享控制框架由主端遥操作控制器和从端自主控制器组成，如图 4所示，主端双模态的输入信号包括力反馈手控器信号和视线信号。手控器把末端关节的位置信息转化为编队的控制命令，控制编队的线速度、角速度和尺寸。视线信号作为双模态的另一路输入信号，通过编队切换控制器转换为编队切换命令，发送给从端编队使其切换为期望队形，从端编队是基于虚拟结构和人工势场法构建的。

所谓共享概念可通过图 4中绿色框描述的主端遥操作控制和黄色框描述的从端自主控制展现出来。具体是指操作员利用主端双模态输入接口里的力反馈手控器和眼动仪分别控制编队系统的行进动作和队形切换动作，从端编队系统的队形保持、外部避障和内部避碰动作是由本地自主控制完成的。

3.1 主端遥操作控制分析

主端双模态输入信号可以映射为虚拟结构的运动特性，包括编队速度、编队尺寸和编队形状。力反馈手控器的$ x $轴和$ y $轴位置转化为虚拟结构的线速度和角速度：

$ \begin{align} \begin{cases} v_{v} =f_{v}^{\rm u} ({\mathit{\boldsymbol{q}}}_{\rm s})=\frac{1}{n}\sum\limits_{i=1}^n {v_{i}} \\ v_{w} =f_{w}^{\rm u} ({\mathit{\boldsymbol{q}}}_{\rm s})=\frac{1}{n}\sum\limits_{i=1}^n {w_{i}} \end{cases} \end{align} $

(6)

式中$ v_{i} $和$ w_{i} $分别表示$ i $第个虚拟点的线速度和角速度。当编队系统躲避障碍物时，距离障碍物最近的移动机器人速度会发生变化，从而产生一个反馈力$ {\mathit{\boldsymbol{F}}}_{\rm m} $，该反馈力表示编队实际速度和主端发布速度两者的差值，并把该力反馈给手控器：

$ \begin{align} \begin{cases} { {f}}_{{\rm m}x}\! =\! k_{{\rm m}x} (v_{v}^{\rm d} -f_{v}^{\rm u} ({\mathit{\boldsymbol{q}}}_{\rm s}))\! =\! k_{{\rm m}x} \left(v_{v}^{\rm d} -\frac{1}{n}\sum\limits_i^n {v_{i}}\right) \\ { {f}}_{{\rm m}y}\! =\! k_{{\rm m}y} (v_{w}^{\rm d} -f_{w}^{\rm u} ({\mathit{\boldsymbol{q}}}_{\rm s}))\! =\! k_{{\rm m}y} \left(v_{w}^{\rm d} -\frac{1}{n}\sum\limits_i^n {w_{i}}\right) \\ {\mathit{\boldsymbol{F}}}_{{\rm m}x} =[{ {f}}_{{\rm m}x}, 0, 0], \; \; {\mathit{\boldsymbol{F}}}_{{\rm m}y} =[{ {f}}_{{\rm m}y}, 0, 0]\\ {\mathit{\boldsymbol{F}}}_{\rm m} ={\mathit{\boldsymbol{F}}}_{{\rm m}x} +{\mathit{\boldsymbol{F}}}_{{\rm m}y} \end{cases} \end{align} $

(7)

其中，$ {\mathit{\boldsymbol{F}}}_{{\rm m}x} $和$ {\mathit{\boldsymbol{F}}}_{{\rm m}y} $分别表示反馈到手控器$ x $、$ y $轴的力。

在手控器的$ x $和$ y $轴控制编队保持某一队形向前运动的过程中，手控器的$ z $轴位置可以映射为此时编队的尺寸，$ z<0 $时保持正常尺寸，$ z>0 $时增大编队尺寸。每个虚拟点距离虚拟结构中心的平均距离定义为编队尺寸，可以表达为

$ \begin{align} f_{\rm s}^{\rm t} ({\mathit{\boldsymbol{q}}}_{\rm s} {\rm)=}\frac{1}{n}\sum\limits_{i=1}^n {\sqrt{(q_{{\rm s}ix} -f_{x}^{\rm t})^{2}+(q_{{\rm s}iy} -f_{y}^{\rm t})^{2}}} \end{align} $

(8)

其中，$ f_{x}^{\rm t} =\dfrac{1}{n}\sum\limits_{i=1}^n {q_{{\rm s}ix}} $，$ f_{y}^{\rm t} =\dfrac{1}{n}\sum\limits_{i=1}^n {q_{{\rm s}iy}} $，二者分别表示虚拟结构的中心在$ x $和$ y $轴的坐标值，则$ \sqrt{(q_{{\rm s}ix} -f_{x}^{\rm t})^{2}+(q_{{\rm s}iy} -f_{y}^{\rm t})^{2}} $表示第$ i $个虚拟点到虚拟结构中心的距离。

对于一些更复杂的场景，机器人编队系统必须能够自由切换队形以在最短的时间内到达目标点。如果再把手控器的位置信息映射为队形切换命令，则不仅造成映射关系的耦合，还会降低控制效率。把视线信号作为另一路输入信号，根据主端的眼动仪命令函数，通过操作人员的注视点$ q_{{\rm{ep}}i} $和注视持续时间$ q_{{\rm{et}}i} $来向从端编队发布队形切换命令。

遥操作编队行进控制原理如图 5所示，首先设置一个虚拟圆，圆心$ O $坐标为$ ( {x_{\rm c}, y_{\rm c}} $)，半径大小为$ r $，在收敛控制器的作用下，每个虚拟点被强行拉到虚拟圆内的点$ p_{i} $坐标$ ({x_{i}, y_{i}} $) 处。圆心$ O $和点$ p_{i} $之间的马氏距离可以表示为

$ \begin{align} d_{\rm M} ({\mathit{\boldsymbol{p}}}_{i}) & =\sqrt{({\mathit{\boldsymbol{p}}}_{i} -{\mathit{\boldsymbol{O}}}){\mathit{\boldsymbol{M}}}^{-1}({\mathit{\boldsymbol{p}}}_{i} -{\mathit{\boldsymbol{O}}})^{\rm T}} \end{align} $

(9)

$ \begin{align} {\mathit{\boldsymbol{M}}} & = \begin{bmatrix} r^{2} & 0 \\ 0 & r^{2} \end{bmatrix} \end{align} $

(10)

收敛控制器的输出$ u_{\rm GC}^{\rm i} =k_{\rm{gc}} \sum {g_{t} (i)} $表示驱动第$ i $个虚拟点到虚拟圆内，$ g_{t} (i) $可以表示为

$ \begin{align} g_{t} (i)= \begin{cases} d_{\rm M} ({\mathit{\boldsymbol{p}}}_{i, t}^{\rm d}), & d_{\rm M} ({\mathit{\boldsymbol{p}}}_{i, t}^{\rm d})\geqslant 1 \\ d_{\rm M} ({\mathit{\boldsymbol{p}}}_{i, t}^{\rm d})-1, & d_{\rm M} ({\mathit{\boldsymbol{p}}}_{i, t}^{\rm d})<1 \end{cases} \end{align} $

(11)

其中$ k_{\rm{gc}} $是收敛系数，$ {\mathit{\boldsymbol{p}}}_{i, t}^{\rm d} $表示第个虚拟点在$ t $时刻的期望位置。虚拟点在圆内形成一个三角形的虚拟结构，而且能够接收到主端发布的速度和队形切换命令，在虚拟结构向目标点$ {\mathit{\boldsymbol{T}}}=[x_{\rm g}, y_{\rm g} ] $移动的过程中，虚拟圆的运动特性可以描述为

$ \begin{align} \begin{bmatrix} x_{\rm c} \\ y_{\rm c} \\ v_{v} \\ \theta \\ r \end{bmatrix}_{t+1} = \begin{bmatrix} x_{\rm c} \\ y_{\rm c} \\ v_{v} \\ \theta \\ r \end{bmatrix}_{t} +{\rm d}t \begin{bmatrix} v_{v} \cdot \cos \theta_{t} \\ v_{v} \cdot \sin \theta_{t} \\ 0 \\ 0 \\ 0 \end{bmatrix}_{t} + \begin{bmatrix} 0 \\ 0 \\ v_{\rm{add}} \\ {\rm d}t\cdot v_{w} \\ 0 \end{bmatrix}_{t} \end{align} $

(12)

式中，$ v_{v} $和$ v_{w} $是编队行进速度，$ v_{\rm{add}} $表示编队速度$ v_{v} $的增量。

3.2 从端自主控制分析

主端双模态信号转换为从端虚拟结构的速度方向和队形切换命令之后，从端虚拟点之间的避碰、虚拟结构与外部环境之间的避障、虚拟结构的队形维持都是由本地自主完成。在虚拟结构的基础上设计3种人工势场函数：虚拟点—障碍物外部避障势场函数、虚拟点—虚拟点内部避碰势场函数、虚拟点—虚拟点队形保持势场函数。在人工势场函数的作用下，编队系统不仅能够完成上面3种自主任务，而且表现出像一个可变形的结构，具有较高的灵活性和可扩展性。

1) 外部避障势场函数

设计一种合适的外部避障势场函数能够减少编队系统任务完成时间、提高效率。本文设计的外部避障势场函数可以描述为

$ \begin{align} f_{{ o}_{ j}}^{\rm s} ({\mathit{\boldsymbol{q}}}_{\rm s})=\sum\limits_{i=1}^n { \left(\min \left\{{0, \frac{d(i, o_{j})^{2}-d_{{\rm R}_{\rm o}}^{2}}{d(i, o_{j})^{2}-d_{{\rm r}_{\rm o}}^{2}}} \right\}\right)}^{2} \end{align} $

(13)

式中，$ d(i, o_{j}) $表示第$ i $个虚拟点与第$ j $个障碍物之间的距离，$ d_{{\rm R}_{\rm o}} $表示避障距离，$ d_{{\rm r}_{\rm o}} $表示安全距离，且$ d_{{\rm R}_{\rm o}} >d_{{\rm r}_{\rm o}} $，在避障过程中需保证$ d(i, o_{j})>d_{{\rm r}_{\rm o}} $。

2) 内部避碰势场函数

考虑到虚拟点之间的摩擦，设计一种内部避碰势场函数：

$ \begin{align} f_{{ r}_{ j}}^{\rm s} ({\mathit{\boldsymbol{q}}}_{\rm s})=\sum\limits_{i=1}^n {\left(\min \left\{{0, \frac{d(i, {{ r}_{ j}})^{2}-d_{{\rm R}_{\rm r}}^{2}}{d(i, {{ r}_{ j}})^{2}-d_{{\rm r}_{\rm r}}^{2}}}\right\}\right)}^{2} \end{align} $

(14)

式中，$ d(i, j) $是第$ i $个虚拟点与第$ j $个虚拟点之间的距离，$ d_{{\rm R}_{\rm r}} $表示虚拟点之间的避碰距离，$ d_{{\rm r}_{\rm r}} $是最小安全距离，在内部避碰的过程中需保证$ d(i, {{ r}_{ j}}) $ $ > $ $ d_{{\rm r}_{\rm r}} $。

3) 队形保持势场函数

设计一种队形保持势场函数来维持队形形状，防止编队发散：

$ \begin{align} f_{\rm f}^{\rm s} ({\mathit{\boldsymbol{q}}}_{s})=\sum\limits_{i=1}^n {((q_{xi} -q_{xi}^{\rm d})^{2}+(q_{yi} -q_{yi}^{\rm d})^{2})} \end{align} $

(15)

式中，$ q_{xi}^{\rm d}, q_{yi}^{\rm d} $分别表示第$ i $个机器人期望位置的$ x $、$ y $位置坐标。

4 实验（Experiment） 4.1 实验平台

基于双模态人机接口的编队系统平台搭建如图 6所示。该系统由1台带有图形用户界面的上位机、1台力反馈手控器设备、1个眼动仪、1个操作员、5个移动机器人组成。图形用户界面包括队形选择区域以及视觉反馈区域。界面上的透明圆圈为操作员的视线焦点。当操作员盯着界面中的三角形时，眼动仪捕捉到操作员的视线信号，界面上的透明圆圈随之移动到三角形区域，此时界面中的三角形会以固定的频率闪烁，代表队形选择成功，将队形切换命令发送给从端编队系统。操作员通过界面下方的视觉反馈区域可以观察到从端实际队形变化情况。

4.2 单模态控制下避障及尺寸变化实验

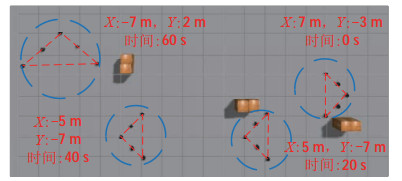
本实验在共享控制框架的基础上验证单模态控制下机器人编队的避障及尺寸变化。如图 7所示，主端的操作员通过力反馈手控器控制从端机器人编队的平均线速度和角速度，引导机器编队以默认的队形（三角形）前行，而且可以实时改变尺寸大小。

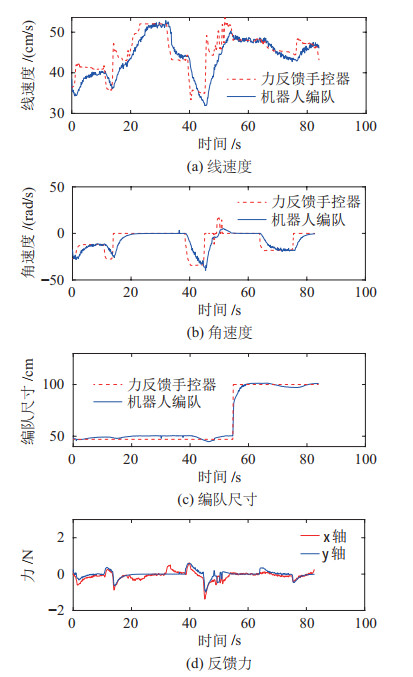
单模态控制下从端编队对主端命令的跟踪实验结果如图 8所示，在0~57 s，操作员操纵力反馈手控器使机器人编队以紧密的三角形队形前行。当机器人编队转弯时，线速度减小，角速度不再为0。在第一次转向后，操作员使力反馈手控器末端位置处于目标角速度的缓冲区，即目标角速度为0，并提高从端机器人编队的线速度。57 s左右操作员通过控制力反馈手控器的$ z $轴位置改变编队尺寸。在整个过程中，当期望的速度突然改变时，由于机器人编队需要时间来响应主端的命令，所以期望速度和实际速度并不匹配，如图 8(a)和图 8(b)所示。此时，主端操作员可以通过力反馈手控器感受不匹配程度，并及时作出相应的应对措施。

4.3 双模态控制下队形切换实验

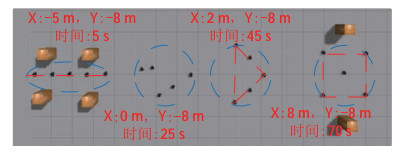
如图 9所示，主端操作员引导机器人编队系统通过一个特殊的长方形通道。本文预先定义了机器人编队的4种队形。编队命令和预定义队形之间的映射关系如表 1所示。这些队形的图案显示在图形用户界面上。操作员经过训练，可以通过眼动仪远程控制从端机器人编队的队形切换。

双模态控制下编队对主端命令的跟踪实验结果如图 10所示，在0~20 s时，操作者控制力反馈手控器引导机器人编队保持一定的速度和尺寸移动，保持编队形状为直线形。20 s后机器人编队安全通过通道。操作员盯着屏幕上的三角形队形持续1 s后，眼动仪识别出操作员的意图，机器人编队的形状变成三角形。与此同时操作人员将力反馈手控器的末端向上移动，扩大编队尺寸。在58 s时操作员盯着屏幕上的正方形持续1 s，从端编队系统切换队形为正方形，并通过力反馈手控器将队形尺寸降低到之前的尺寸。

4.4 单模态和双模态对比试验

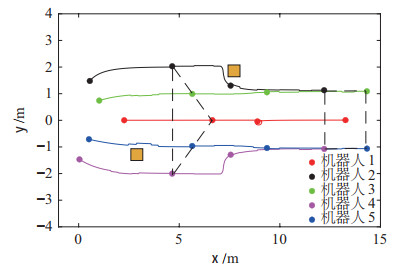
实验场景选为4 m$ \times $15 m的走廊，实验任务是证明相对于传统的单模态双边遥操作控制，融合视线跟踪的双模态编队控制能够降低操作负荷、提高控制效率。如图 11所示，前4张图片和后4张图片分别表示在单模态和双模态控制下编队系统在第0 s、25 s、34 s、53 s的状态，图 12表示编队的运动轨迹，在$ x= $ 2.5 m处避障，在$ x= $ 7.5 m处开始切换队形为正方形。

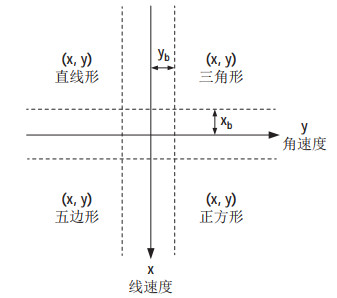
文中设计的3种势场算法在移动机器人搭载的微型单板计算机树莓派3B$ + $上运行，所以编队系统在行进过程中能够维持编队收敛，保持一个稳定队形。当遇到障碍物时也可以自主躲避障碍物，队形切换时执行内部避碰算法避免内部摩擦。双模态场景下，把手控器末端关节的$ x $轴和$ y $轴位置信息映射为编队系统的行进命令，眼动仪根据表 1映射关系向编队系统发布队形切换命令。单模态场景下，通过手控器向编队系统发布编队行进命令，在$ - y_{\rm b}<y<y_{\rm b} $区间内将$ x $轴位置信息映射为线速度，在$ - x_{\rm b}<x<x_{\rm b} $区间内将$ y $轴位置信息映射为角速度。如果$ x , y $坐标在图 13所示的虚线之外，则根据不同的位置信息可映射得到不同的队形切换命令，受限于手控器的机械特性，为防止命令映射关系耦合，编队行进命令和队形切换命令不能同时发布。

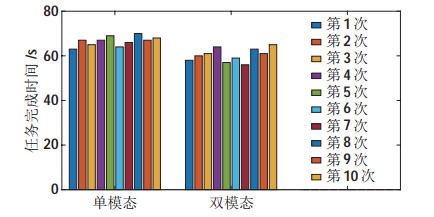
该实验分别在单模态控制和双模态控制下重复10次，每次实验从起点到终点的用时记录如图 14所示，单模态控制模式下平均用时66.6 s，双模态控制模式下平均用时60.4 s，控制效率提高了9.309%。基于这个结果提出一个假设，即随着场地的增大和任务时间的增加，双模态较单模态的控制效率提高更加明显。由于受实验室场地等限制，在Gazebo仿真环境里另外搭建3个场景，场景1的大小是4 m$ \times $20 m，场景2的大小是12 m $ \times $12 m，场景3的大小是16 m$ \times $16 m。单模态和双模态的任务完成时间和效率提升情况如表 2所示，符合提出的假设。

为了验证融合眼动仪的双模态控制能够减轻操作人员工作负荷，提供一个更加直观的控制方式，设计图 15所示的问卷，让10个志愿者在重复单模态和双模态对比实验之后对问卷上的8个问题进行评分。调查结果显示，参与者普遍认为融合眼动仪的双模态控制能够缓解操作员的精神紧张程度、减轻操作负荷、提高控制效率。

5 结论（Conclusion）

本文针对传统的基于手控器单模态人机接口的移动机器人编队控制系统中存在的复杂运动控制效果差的问题，提出了一种基于双模态人机接口的编队共享控制方法。将主端不同的输入模态映射为不同的遥操作命令，从端编队系统被视为由多个虚拟点组成的虚拟结构，结合人工势场函数实现自主控制。设计了避障及尺寸变化实验来验证手控器作为输入模态的可行性，设计了队形变化实验来验证眼动仪作为输入模态控制队形的可行性。最后设计了单模态和双模态对比试验，证明了双模态控制较单模态控制而言不仅能够减轻操作人员的工作负荷，还可以提高控制效率，4种场景下效率分别提升了9.309%、11.14%、15.098% 和17.42%，随着场地的增大和任务时间的增加，双模态较单模态的控制效率提升更加明显。