1 引言（Introduction）

近年来，随着科学技术的不断进步，机器人导航技术得到了充分的发展，而同时定位和地图构建（SLAM）作为机器人导航的核心技术，也得到了广泛的应用。尤其是基于相机的SLAM系统，因其可以直接利用相机提供的场景信息，实现对机器人的定位和场景地图的构建而受到重视。目前较为成熟的视觉SLAM系统有MonoSLAM（monocular SLAM）^[1]、PTAM（parallel tracking and mapping）^[2]、ORB-SLAM2^[3]、LSD-SLAM（large-scale direct-SLAM）^[4]、SVO（semi-direct monocular visual odometry）^[5]、DSO（direct sparse odometry）^[6]等。

现阶段多数的SLAM系统是在纹理丰富和静态环境的假设下提出的，然而，在实际环境中难以避免地存在运动物体，而运动物体的存在往往使得系统获得错误的数据关联，最终导致建图精度严重下降。因此，如何在实际场景中将正确的数据关联加入SLAM系统中、实现相机的精准定位和稠密地图的准确构建已经成为一个重要的研究方向。

动态场景下视觉SLAM算法往往采用动态区域剔除的方式消除相机姿态与地图点之间错误的数据关联，而根据是否将语义信息加入算法，动态区域剔除分为深度学习和几何算法两种方式。

深度学习方式是利用深度学习网络检测语义动态目标，如Bescos等^[7]提出的DynaSLAM算法利用Mask R-CNN^[8]进行语义动态物体识别，并结合多视几何一致性检测运动目标，但该算法只能用于数据集的动态分割，无法满足实际场景下实时性的要求。FlowFusion算法^[9]在StaticFusion算法^[10]的基础上进行动态点云的识别与分割，该算法使用PWC-Net网络^[11]实现对动态物体从2维到3维的场景流识别与移除，并通过最小化空间和强度误差获得动态移除后的相机位姿。

在采用几何算法的研究方法中，Tan等^[12]提出的RDSLAM（robust monocular SLAM）算法基于先验的自适应的RANSAC（random sample consensus）算法^[13]，可以有效地去除场景中孤立的动态点，并提出了在线关键帧更新的机制，替换掉运动物体比重过大的关键帧，但是当动态场景像素点数量超过静态场景像素点时，RANSAC算法难以将动态场景剔除，降低了系统定位的精度。Li等^[14]采用一种关键帧深度边缘点静态权重的算法检测和剔除动态目标，而后通过IAICP（intensity assisted ICP）算法^[15]和静态权重减弱动态物体对静态点云地图的影响。Zhou等^[16]使用双目视觉实现相邻图像帧之间的特征点匹配，而后根据全局图像运动流（global image motion flow，GIMF）和测量光流（measured optical flow，MOF）^[17]计算残余图像运动流（residual image motion flow，RIMF）^[18]，判定当前像素是否运动，从而完成动态区域的分割，然而在相机做三轴旋转运动时，光流计算易于受到噪声的影响，动态物体的判定不够完整，降低了系统的精度。

本文在ORB-SLAM2算法^[3]与稠密直接法的基础上，提出一种动态环境下的RGB-D SLAM算法^[19-21]。首先，利用语义动态补全算法实现语义动态物体的完整检测，然后利用高斯－牛顿算法结合动态耦合分数值完成对相机位姿的解算，并添加空间数据关联算法优化相机姿态。最后，在相机姿态和地图点的基础上，构建可以实时更新的静态八叉树地图。与现有的开源算法ORB-SLAM2和DS-SLAM作对比，本文算法能完整地移除动态区域，因此，具有更高的定位和建图精度。

2 SLAM算法的流程（Process of the SLAM algorithm） 2.1 算法框架

算法的整体流程如图 1所示，包括语义动态补全、稠密直接法、特征点法和地图构建4个模块。在语义动态补全环节，首先根据SegNet语义网络^[22]获得初始语义动静态区域，然后利用相邻语义判定法获得当前像素点的语义状态信息$ W_{\rm c}(\mathit{\boldsymbol{x}}) $，最后，通过边缘轮廓判定，进一步完善语义动态物体信息。在稠密直接法模块，利用几何误差和语义误差作为最小能量函数，并结合空间平面一致性判据判断、动态区域剔除和深度信息筛选等操作获得的动态耦合分数值，实现不同语义类别的分类处理，完成对相机位姿的解算。在相机姿态的基础上，采用空间数据关联算法获得相机姿态的置信度，即利用3D地图点集与当前帧特征点匹配的数目完成对相机位姿的置信度评估，进而判定是否采用特征点法对相机位姿进行优化。在特征点法环节，通过相机姿态实现3D地图点的实时更新，并利用局部BA（bundle adjustment）法和闭环优化线程获得更为准确的地图点和相机姿态。最后，在相机姿态和3D地图点的基础上，结合语义动态物体，实现从2维到3维的动态区域剔除，从而构建不包含动态信息的八叉树稠密地图。

2.2 语义动态补全

首先使用SegNet语义网络^[22]对彩色图像进行处理，获取图像语义信息。根据语义识别结果，将图像像素点划分为语义动态物体$ D_{\rm f} $、语义静态物体$ S_{\rm j} $以及其他区域$ S_{\text{else}} $。其中语义动态物体是以人和动物为代表的具有潜在运动可能性的物体，语义静态物体是以显示屏、桌子为主的不具有主动运动趋势的物体，而其他物体则是语义分割网络不能识别的场景区域。

然而，当图像出现运动模糊且相机出现三轴旋转运动时，语义分割网络难以实现对语义动静态物体的完整检测（如图 2(b)所示，行人无法被检测完整）。如果在动态区域剔除环节中将语义动态物体作为唯一动态物体进行剔除，则动态区域无法被完整移除，导致相机定位精度严重下降，因此，需要进一步对语义动态区域进行细分。

当同时提取边缘特征和语义信息时，可以发现，行人的轮廓内部信息既包含了初始语义图像中行人的信息，也涵盖了语义网络漏检的行人信息（如图 2(c)和2(b)所示），即行人的轮廓内部区域是完整的语义动态区域。在此基础上，可以通过对初始语义动态物体的深度信息和边缘轮廓分析，实现完整语义动态物体的检测。

具体地，对存在的RGB图像，首先需要对图像进行类型转化，将其转化为灰度图像，然后，在拉普拉斯算子提取图像边缘特征的基础上（见图 2(c)），利用OpenCV软件库中的findContours() 函数获得与每个边缘轮廓相对应的轮廓内部的角点数组。在此基础上，利用相邻语义判定获得像素点语义状态信息$ W_{\rm c}(\mathit{\boldsymbol{x}}) $，实现对当前像素点语义状态的判定，并且根据状态信息完成对每个轮廓的筛选，进而实现对未知区域的扩展和孤立区域的移除，最后完成对补充和移除区域像素点$ W_{\rm c}(\mathit{\boldsymbol{x}}) $的重置。

假设$ \mathit{\boldsymbol{x}} $为图像帧上的2维图像坐标，当前图像帧每个像素点既有深度信息$ Z_{\rm c}(\mathit{\boldsymbol{x}}) $，也包含参考关键帧语义状态信息$ W_{\rm k}(\mathit{\boldsymbol{x}}) $，两者是一一对应的。因此，可以利用$ Z_{\rm c}(\mathit{\boldsymbol{x}}) $和$ W_{\rm k}(\mathit{\boldsymbol{x}}) $判断当前像素点是否属于语义动态物体$ D_{\rm f} $。首先计算初始语义动态物体$ D_{\rm f} $的平均深度$ \bar Z_{\rm f} $：

$ \begin{align} \bar Z_{\rm f} = \left(\sum\limits_{x \in N_{\rm ini}} {Z_{\rm c}(\mathit{\boldsymbol{x}})}\right)\Big/{\rm nums}(N_{\rm ini}) \end{align} $

(1)

其中$ N_{\rm ini} $为初始语义动态信息像素点集合，函数$ {\rm nums}(N_{\rm ini}) $为求集合$ N_{\rm ini} $中点的数目。相邻语义判定是根据初始语义动态物体的深度信息，对当前像素点语义状态$ W_{\rm c}(\mathit{\boldsymbol{x}} $) 进行判断，也就是说，当前像素点的深度值与$ \bar Z_{\rm f} $越接近，则与$ \bar Z_{\rm f} $为同种类型的可能性越大，但基于深度信息的$ W_{\rm c}(\mathit{\boldsymbol{x}}) $不能有效地利用语义动态信息，造成系统对语义信息甄别不完整。因此，$ W_{\rm c}(\mathit{\boldsymbol{x}}) $增加了参考关键帧中的状态信息$ W_{\rm k}(\mathit{\boldsymbol{x}}) $用以调整当前像素点与$ \bar Z_{\rm f} $之间的深度差值$ Z_{\rm r}(\mathit{\boldsymbol{x}}) $。$ W_{\rm c}(\mathit{\boldsymbol{x}}) $计算公式如下：

$ \begin{align} W_{\rm c}(\mathit{\boldsymbol{x}}) & = Z_{\rm r}(\mathit{\boldsymbol{x}}) [1+ (W_{\rm k}(\mathit{\boldsymbol{x}}) - W_{\text{th}})/{\text{exp}}({Z_{\rm k}^{\rm c}(\mathit{\boldsymbol{x}})})\rbrack \end{align} $

(2)

$ \begin{align} Z_{\rm r}(\mathit{\boldsymbol{x}}) & = |Z_{\rm c}(\mathit{\boldsymbol{x}}) - \bar{Z}_{\rm f}| \end{align} $

(3)

其中，将参考关键帧标注为k，$ W_{\text{th}} $是用作判定语义状态的阈值，$ Z_{\rm k}^{\rm c}(\mathit{\boldsymbol{x}}) $表示参考关键帧与当前图像帧深度差值的绝对值，$ 1+ (W_{\rm k}(\mathit{\boldsymbol{x}}) - W_{\text{th}} )/{\rm e}^{Z_{\rm k}^{\rm c}(\mathit{\boldsymbol{x}})} $为参考关键帧语义调整值。在这里，$ Z_{\rm k}^{\rm c}(\mathit{\boldsymbol{x}}) $越大，代表当前像素点状态$ W_{\rm c}(\mathit{\boldsymbol{x}}) $对参考关键帧像素点状态$ W_{\rm k}(\mathit{\boldsymbol{x}}) $依赖越小。当$ W_{\rm c}(\mathit{\boldsymbol{x}}) $小于$ W_{\text{th}} $时，表示该点处于语义动态物体区域。

经过上述处理，已经获得了像素点的状态值$ W_{\rm c}(\mathit{\boldsymbol{x}}) $，但是，新增的语义动态物体往往存在被错误判断的像素点，难以实现准确检测语义动态物体的目标。为了得到完整的语义动态物体，利用轮廓信息对语义动态像素点进行分析，进而获得语义动态物体的完整轮廓。

具体地，若轮廓内部的语义动态角点数目大于参考阈值，则将该轮廓判定为语义动态轮廓，并将轮廓内部所有角点作为语义动态像素点；否则，移除当前轮廓。最后完成对移除和扩展区域像素点的$ W_{\rm c}(\mathit{\boldsymbol{x}}) $的重置。公式如下：

$ \begin{align} W_{\rm c} (\mathit{\boldsymbol{x}}) = \begin{cases} W_{\text{th}} - a, & {\mathit{\boldsymbol{x}}} \; 位于扩展区域 \\ W_{\text{th}} + a, & {\mathit{\boldsymbol{x}}} \; 位于移除区域 \\ W_{\rm c}(\mathit{\boldsymbol{x}}), & \text{其他} \end{cases} \end{align} $

(4)

其中，$ a $为静态增量常数。

如图 2(d)中蓝色的掩模代表的是初始语义动态信息像素，而绿色的像素点则代表补充的语义信息。

2.3 基于动态耦合的相机位姿估计

在相机位姿解算部分，首先，本文通过动态耦合分数值对图像进行运动分割，实现语义物体的分类处理；然后，在几何误差和语义误差的基础上，利用稠密直接法估计相机的初始位姿。

2.3.1 稠密直接法计算位姿

通过投影函数$ \mathit{\boldsymbol{\pi}}({\rm R}^{3} \to {\rm R}^{2}) $与当前帧和参考关键帧之间的位姿变换矩阵$ \mathit{\boldsymbol{T}}_{\rm c}^{\rm k} $，可以构建函数$ \mathit{\boldsymbol{\tau}}(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{T}}_{\rm c}^{\rm k}) $实现前后图像帧之间像素坐标的转化：

$ \begin{align} \mathit{\boldsymbol{x}}' = \mathit{\boldsymbol{\tau}}(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{T}}_{\rm c}^{\rm k}) = \pi ({\mathit{\boldsymbol{T}}}^{\rm k}_{\rm c} \pi^{-1}({\mathit{\boldsymbol{x}}}, Z_{\rm c}({\mathit{\boldsymbol{x}}}))) \end{align} $

(5)

式中$ \mathit{\boldsymbol{x}} $和$ \mathit{\boldsymbol{x}}' $为当前图像帧像素坐标和参考关键帧的像素坐标，而$ \mathit{\boldsymbol{\pi}}^{- 1}(\mathit{\boldsymbol{x}}, Z_{\rm c}(\mathit{\boldsymbol{x}})) $为逆投影函数，实现2维坐标向3维坐标的转换。稠密直接法是通过最小化强度误差$ r_{\rm I} $和深度误差$ r_{\rm z} $实现对相机姿态的估计。其中，$ r_{\rm I}(\mathit{\boldsymbol{x}}) $和$ r_{\rm z}(\mathit{\boldsymbol{x}}) $几何误差定义为

$ \begin{align} r_{\rm I}(\mathit{\boldsymbol{x}}) & = I_{\rm k}(\mathit{\boldsymbol{\tau}}(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{T}}_{\rm c}^{\rm k})) - I_{\rm c}(\mathit{\boldsymbol{x}}) \end{align} $

(6)

$ \begin{align} r_{\rm z}(\mathit{\boldsymbol{x}}) & = Z_{\rm k}(\mathit{\boldsymbol{\tau}}(\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{T}}_{\rm c}^{\rm k})) - | \mathit{\boldsymbol{T}}_{\rm c}^{\rm k}\mathit{\boldsymbol{\pi}}^{- 1}(\mathit{\boldsymbol{x}}, Z_{\rm c}(\mathit{\boldsymbol{x}})) |_{\rm z} \end{align} $

(7)

$ Z_{\rm k}(\mathit{\boldsymbol{x}}) $和$ I_{\rm k}(\mathit{\boldsymbol{x}}) $为当前像素点在参考关键帧图像中的深度和强度值，$ | \cdot |_{\rm z} $为求当前3维点的深度值。

$ h_{\rm c}(\mathit{\boldsymbol{x}}) $为当前像素点的语义类别，参数$ p_{\rm y}(\mathit{\boldsymbol{x}}) $为当前图像帧的语义权重：

$ \begin{align} p_{\rm y}(\mathit{\boldsymbol{x}}) = \begin{cases} 1, & h_{\rm c}(\mathit{\boldsymbol{x}}) \in D_{\rm f} \\ 0.5, & h_{\rm c}(\mathit{\boldsymbol{x}}) \in S_{\rm j} \\ 0, & h_{\rm c}(\mathit{\boldsymbol{x}}) \in S_{\text{else}} \end{cases} \end{align} $

(8)

其中，$ D_{\rm f} $、$ S_{\rm j} $和$ S_{\text{else}} $依次为语义动态物体、语义静态物体和其他物体。

在几何误差的基础上，本文增加了语义误差$ R_{\rm y}(\mathit{\boldsymbol{x}}) $用以加强相机位姿与场景的数据关联。语义误差$ R_{\rm y}(\mathit{\boldsymbol{x}}) $为

$ \begin{align} R_{\rm y}(\mathit{\boldsymbol{x}}) = p_{\rm y}(\mathit{\boldsymbol{x}}) \times \frac{\sum\limits_{x_{h} \in N_{\rm arc}}{\dfrac{1}{W_{\rm k}(\mathit{\boldsymbol{\tau}} (\mathit{\boldsymbol{x}}_{h}, \mathit{\boldsymbol{T}}_{\rm c}^{\rm k}))}}}{{\rm nums}(N_{\rm arc})} \end{align} $

(9)

在当前帧中以$ \mathit{\boldsymbol{x}} $为圆心、1为半径做圆，$ N_{\rm arc} $为在圆弧上选取的像素点的集合，$ \mathit{\boldsymbol{x}}_{h} $为第$ h $个选取点的坐标。$ R_{\rm y}(\mathit{\boldsymbol{x}}) $是由参考关键帧中选取像素点的语义状态均值和语义权重$ p_{\rm y}(\mathit{\boldsymbol{x}}) $组成的。相机位姿解算如式(10) 所示，是采用误差项完成对相机姿态$ \mathit{\boldsymbol{T}}_{\rm c}^{\rm k} $的估计，并利用动态耦合分数值$ b(\mathit{\boldsymbol{x}}) $确保场景中语义静态和其他物体的误差项具有较高的权重。

$ \begin{align} \mathit{\boldsymbol{T}}_{\rm c}^{\rm k} =\;& \mathop{\text{arg min}}\limits_{\mathit{\boldsymbol{T}}_{\rm c}^{\rm k}} \sum\limits_{x_p \in N_{\text{all}}} \lbrack b(\mathit{\boldsymbol{x}})(F(\omega_{\rm D}r_{\rm Z}(\mathit{\boldsymbol{x}}_{p}))+ \\ & F(\alpha_{\rm I}\omega_{\rm I}r_{\rm I}(\mathit{\boldsymbol{x}}_{p})) + \alpha_{\rm Y}R_{\rm y}(\mathit{\boldsymbol{x}}_{p})) \rbrack \end{align} $

(10)

其中，$ N_{\text{all}} $为像素点集合，$ x_{p} $为集合中的第$ p $个点。参数$ \alpha_{\rm I} $和$ \alpha_{\rm Y} $分别为强度误差和语义误差的转化值，为语义误差和强度误差调整缩放比例，使其具有与深度误差项相同的作用。$ \omega_{\rm D} $和$ \omega_{\rm I} $分别为每个像素点在深度和强度的导数梯度，是在控制外界噪声的情况下，在时间和空间上加权了$ r_{\rm Z} $和$ r_{\rm I} $。而$ F(r) $函数为柯西核函数：

$ \begin{align} F(r) = \frac{c^{2}}{2}\ln \left[1 + \left(\frac{r}{c}\right)^{2}\right] \end{align} $

(11)

其中$ c $表示$ F(r) $的拐点，用来控制较大残差的抑制程度。柯西核函数的引入，是为了消除具有较大几何误差的像素点对SLAM系统的影响。

在$ \mathit{\boldsymbol{T}}_{\rm c}^{\rm k} $和参考关键帧相机姿态$ \mathit{\boldsymbol{T}}_{\rm k}^{\rm w} $的基础上，计算得到当前相机坐标系与世界坐标系的旋转位姿$ \mathit{\boldsymbol{T}}_{\rm c}^{\rm w} $：

$ \begin{align} \mathit{\boldsymbol{T}}_{\rm c}^{\rm w} = \mathit{\boldsymbol{T}}_{\rm c}^{\rm k} \times \mathit{\boldsymbol{T}}_{\rm k}^{\rm w} \end{align} $

(12)

2.3.2 动态耦合

为了完整地消除动态物体的影响，提高相机旋转矩阵求解的准确度，在计算动态耦合分数值$ b(\mathit{\boldsymbol{x}}) $时，选择了以语义类别为基础，分类处理的方式，而非传统的语义动态区域剔除。本文算法在语义动态区域剔除的基础上，增加了对语义静态物体的运动判定及其他物体深度信息的筛选，在一定程度上提升了位姿解算的准确度。

在场景中，根据语义标签信息依次使用动态区域剔除、空间平面一致性判据判断和深度信息筛选的方式计算动态耦合分数值。

动态区域剔除是通过对语义动态区域$ b(\mathit{\boldsymbol{x}}) $的置零，完成对语义动态物体$ D_{\rm f} $的移除，如式(19) 所示。

空间平面一致性是对语义静态物体运动可能性的判定。它分成2个部分，一是空间权重$ p_{\rm s}(\mathit{\boldsymbol{x}}) $，是从3维空间角度出发，利用$ D_{\rm f} $和当前像素点所属类别之间的深度差值作为衡量运动可能性的权重值，二是平面权重$ p_{\rm l}(\mathit{\boldsymbol{x}}) $，是以2维平面为基础，利用当前像素点与$ D_{\rm f} $之间的欧氏距离作为动态物体的判断基准。

空间权重$ p_{\rm s}(\mathit{\boldsymbol{x}}) $是根据语义静态物体$ S_{\rm j} $和语义动态物体$ D_{\rm f} $间的深度差值$ Z_{\rm j}^{\rm f}(\mathit{\boldsymbol{x}}) $计算得到的。$ p_{\rm s}(\mathit{\boldsymbol{x}}) $和$ Z_{\rm j}^{\rm f}(\mathit{\boldsymbol{x}}) $成正相关，即$ Z_{\rm j}^{\rm f}(\mathit{\boldsymbol{x}}) $越大，$ p_{\rm s}(\mathit{\boldsymbol{x}}) $越大。

$ \begin{align} Z_{\rm j}^{\rm f}(\mathit{\boldsymbol{x}}) & = \sum\limits_{x_h \in N_{\rm j}}\dfrac{Z_{\rm j}(\mathit{\boldsymbol{x}}_h) - \bar{Z}_{\rm f}}{{\rm nums}(N_{\rm j})} \end{align} $

(13)

$ \begin{align} p_{\rm s}(\mathit{\boldsymbol{x}}) & = \begin{cases} \dfrac{Z_{\rm j}^{\rm f}(\mathit{\boldsymbol{x}})}{Z_{\text{th2}}}, & Z_{\rm j}^{\rm f}(\mathit{\boldsymbol{x}}_{h}) \in (Z_{\text{th1}}, Z_{\text{th2}}) \\ 0, & \text{其他} \end{cases} \end{align} $

(14)

其中，$ Z_{\rm j}(\mathit{\boldsymbol{x}}_{h}) $为当前像素点所属语义静态类的深度信息存储点集，$ N_{\rm j} $为当前静态类像素点集合，$ x_{h} $为第$ h $个静态像素点，$ \bar{Z}_{\rm f} $为动态物体深度均值。$ Z_{\text{th2}} $和$ Z_{\text{th1}} $为深度信息的上、下阈值，只计算阈值内部的像素点的空间权值$ p_{\rm s}(\mathit{\boldsymbol{x}}) $。根据RGB-D摄像头信息设置参数为$ Z_{\text{th2}} = 5 $，$ Z_{\text{th1}} = 0.3 $。

最后，根据物体运动规律分析，当场景中语义动静态物体一起运动时，运动的语义静态物体$ S_{\rm j} $通常集中在语义动态物体$ D_{\rm f} $周围区域出现。因此，像素点平面权重$ p_{\rm l}(\mathit{\boldsymbol{x}}) $和当前像素点与语义动态物体之间的欧氏距离$ d_{\rm f}(\mathit{\boldsymbol{x}}) $成正相关。$ p_{\rm l}(\mathit{\boldsymbol{x}}) $公式如下：

$ \begin{align} p_{\rm l}(\mathit{\boldsymbol{x}}) & \propto d_{\rm f}(\mathit{\boldsymbol{x}}) \end{align} $

(15)

$ \begin{align} p_{\rm l}(\mathit{\boldsymbol{x}}) & = {\rm {exp}}({- \frac{\alpha^{2}}{{d_{\rm f}(\mathit{\boldsymbol{x}})}^{2}}}) \end{align} $

(16)

其中$ \alpha $为距离转化常数。语义静态物体的动态耦合分数值$ b_{\rm j}(\mathit{\boldsymbol{x}}) $是由空间权重$ p_{\rm s}(\mathit{\boldsymbol{x}}) $、语义权重$ p_{\rm y}(\mathit{\boldsymbol{x}}) $和像素点平面权重$ p_{\rm l}(\mathit{\boldsymbol{x}}) $组成的。深度误差$ Z_{\rm j}^{\rm f}(\mathit{\boldsymbol{x}}) $和欧氏距离$ d_{\rm f}(\mathit{\boldsymbol{x}}) $越大，表示当前像素点与语义动态物体之间存在缓冲区域，因此，当前像素点的运动可能性越低，而动态耦合分数值$ b(\mathit{\boldsymbol{x}}) $越大。故语义静态物体的动态耦合分数值$ b_{\rm j}(\mathit{\boldsymbol{x}}) $与$ p_{\rm s}(\mathit{\boldsymbol{x}}) $和$ p_{\rm l}(\mathit{\boldsymbol{x}}) $成正相关，公式如下：

$ \begin{align} b_{\rm j}(\mathit{\boldsymbol{x}}) = (1 - p_{\rm y}(\mathit{\boldsymbol{x}}))p_{\rm s}(\mathit{\boldsymbol{x}})p_{\rm l}(\mathit{\boldsymbol{x}}) + h \end{align} $

(17)

其中$ h= 0.3 $是设定好的常数，表示阈值基准值。

对于SegNet网络不能识别的区域$ S_\text{else} $，利用深度信息筛选的方式获得分数值$ b_{\text{else}}(\mathit{\boldsymbol{x}}) $，即使用阈值完成对深度信息的判定。若超出阈值，则采用较小的分数值。分数值$ b_{\text{else}}(\mathit{\boldsymbol{x}}) $如下：

$ \begin{align} b_{\text{else}} (\mathit{\boldsymbol{x}}) = \begin{cases} 0.4, & Z_{\text{else}}(\mathit{\boldsymbol{x}}) \in (Z_{\text{th1}}, Z_{\text{th2}}) \\ 0.1, & \text{其他} \end{cases} \end{align} $

(18)

而$ b_{\text{else}}(\mathit{\boldsymbol{x}}) $和$ b_{\rm j}(\mathit{\boldsymbol{x}}) $构成了动态耦合分数值$ b(\mathit{\boldsymbol{x}}) $：

$ \begin{align} b(\mathit{\boldsymbol{x}}) = \begin{cases} 0, & {p}_{\rm y} (\mathit{\boldsymbol{x}}) = 1 \\ b_{\text{else}} (\mathit{\boldsymbol{x}}), & {p}_{\rm y}(\mathit{\boldsymbol{x}}) = 0 \\ b_{\rm j}(\mathit{\boldsymbol{x}}), & \text{其他} \end{cases} \end{align} $

(19)

$ b(\mathit{\boldsymbol{x}}) $越大，表示像素点在相机姿态估计环节的贡献越大，此时运动物体对于SLAM系统的影响减弱。

2.4 空间数据关联

空间数据关联是通过相机位姿$ \mathit{\boldsymbol{T}}_{\rm c}^{\rm w} $置信度$ W $将特征点法和直接法结合在一起的。空间数据关联一方面加强了相机姿态与地图点集$ K = \{k_{1}, \cdots, $ $ k_{n - 1}, k_{n}\} $之间的数据关联，另一方面，可以判定是否采用特征点法对当前相机姿态$ \mathit{\boldsymbol{T}}_{\rm c}^{\rm w} $进行优化，减小了系统的累积漂移误差。本文姿态置信度$ W $的计算满足以下几个规则：

(1) 第1帧置信度$ W $的值为0。

(2) 置信度$ W $的获取如式(20) 所示，是在地图点集$ K $和当前姿态$ \mathit{\boldsymbol{T}}_{\rm c}^{\rm w} $的基础上，利用当前帧特征点与地图点之间的匹配数目$ t $完成的。若$ t $大于阈值，则$ W $置1，输出相机位姿；否则，采用特征点法优化当前相机姿态。

$ \begin{align} W = \begin{cases} 1, & t > t_{\text{th}} \\ 0, & \text{其他} \end{cases} \end{align} $

(20)

特征点法位姿优化分成3个部分，地图点创建、局部BA和闭环优化进程，如图 1所示。首先，在特征点匹配的基础上，利用相机姿态实时更新3D地图点集$ K $，构建局部地图。然后，使用局部BA算法，将当前帧与地图点集$ K $相匹配，获得重投影误差，进而实现对离群的地图点的剔除和相机姿态的优化，最后，采用闭环优化进程，消除视觉里程计产生的累积漂移误差。空间数据关联结构如图 3所示。

2.5 静态地图构建

为了获得更加准确和详细的地图，本文选择构建八叉树稠密地图^[23]，相比于稀疏地图，它可以确保移动机器人在不同场景下的工作更加高效。基于八叉树模型的地图将2维像素点转化为3维八叉树节点，每个八叉树节点保存当前节点的占据状况。由于语义分割的精度有限，因此在八叉树地图中，采用log分数值结合节点权重值$ p(\mathit{\boldsymbol{x}}) $的方法，减小动态对象带来的影响。像素点被占用的概率为$ i $，$ y $则代表当前概率的对数分数值，可以通过logit变换计算而来：

$ \begin{align} y = \text{logit}(i) = \ln\frac{i}{1 - i} \end{align} $

(21)

本文在计算$ y $的基础上，添加节点权重值$ p(\mathit{\boldsymbol{x}}) $用以移除动态地图点。通过语义动态物体的深度均值$ \bar{Z}_{\rm f} $和当前节点的深度$ Z_{1}(\mathit{\boldsymbol{x}}) $，实现节点权重值$ p(\mathit{\boldsymbol{x}}) $的计算，公式如下：

$ \begin{align} Z_{\rm s}(\mathit{\boldsymbol{x}}) & = |\bar Z_{\rm f} - Z_{1}(\mathit{\boldsymbol{x}})| \end{align} $

(22)

$ \begin{align} p(\mathit{\boldsymbol{x}}) & = \begin{cases} 0, & Z_{\rm s}(\mathit{\boldsymbol{x}}) < Z_{\text{th}} \\ 1, & \text{其他} \end{cases} \end{align} $

(23)

其中，$ Z_{\text{th}} $为深度阈值，$ Z_{\rm s}(\mathit{\boldsymbol{x}}) $为节点深度差值，$ x $为节点2维坐标。当权重值$ p(\mathit{\boldsymbol{x}}) $置0时，该节点占据状况被清除；当其为1时，当前节点被占据。在保存足够$ S_{\rm j} $节点的前提下，减小了动态物体对地图精度的影响。

3 实验分析（Experiment analysis）

本节从语义动态信息补全、视觉里程计评估、SLAM定位评估和静态地图构建等4个方面对算法进行检验，并与ORB-SLAM2^[3]、DS-SLAM^[24]、ReFusion^[25]和无空间平面一致性SLAM算法等4种算法在TUM数据集上进行实验对比。

另外，本文算法运行的硬件环境包括：Intel i5-8250U四核1.6 GHz处理器、英伟达Geforce MX110（2 GB）显卡、16 GB内存、1 T硬盘、Ubuntu16.04系统。

3.1 语义动态信息补全

在TUM数据集中动态场景的实验过程如图 4所示。图 4(1)为利用拉普拉斯算子提取的边缘图像，白色线段为图像的边缘信息，黑色区域为轮廓内部区域。图 4(2)是根据SegNet网络获得的语义图像，蓝色区域为语义动态区域，可以发现，语义动态物体并没有被检测完整。因此，为了实现对语义动态物体的完整移除，本文算法在相邻语义判定的基础上，选取图像中语义动态角点大于阈值的边缘轮廓作为语义动态物体的扩展区域，否则排除该区域。最终的检测结果如图 4(3)所示，绿色的像素点是经过边缘轮廓补偿的像素点，可以明显地检测出丢失的部分肢体，实现了语义动态物体对未知区域的扩展。

3.2 视觉里程计评估

为了验证视觉里程计在动态环境下的鲁棒性，使用TUM数据集中RGB-D SLAM数据集作为实验数据，将相对位姿误差（RPE）作为评价指标，而RPE的估计是通过均方根误差（RMSE）的计算获得的，实验结果如表 1所示。

表 1中，将本文算法与ReFusion算法、ORB-SLAM2算法、DS-SLAM算法和无空间平面一致性SLAM算法进行对比，并将TUM数据集根据动态区域的多寡划分为静态、低动态和高动态数据集。ORB-SLAM2算法得益于RANSAC算法对小部分离群动态点的剔除能力，对于低动态和静态场景可以获得精准的相机姿态。ReFusion算法仅通过SDF（signed distance field）算法的表面深度误差实现对动态区域的检测与移除，在运动模糊较为严重的情况下，有可能将部分动态区域当作静态场景处理。因此该算法在高动态环境下性能大幅下降。DS-SLAM算法在ORB-SLAM2系统的基础上，选取语义分割线程和运动一致性方法减小动态物体对相机位姿精度的影响，但是在高动态数据集中，仍然存在语义分割精度较低的问题。对比于本文算法，无空间平面一致性SLAM算法可根据柯西核函数和语义动态区域剔除算法减小动态物体的影响，确保系统在低动态环境下仍有较好的表现。

如表 1所示，在绝大多数的低动态和高动态数据集中，本文算法的误差精度均优于对比算法。其中，在运动场景较为模糊的“fr3/w_r”序列中，当前算法相比于DS-SLAM算法，保持60% 以上的精度提升，而与ReFusion算法和无空间平面一致性算法相比，相机的姿态准确度分别提升了80%和55%以上。

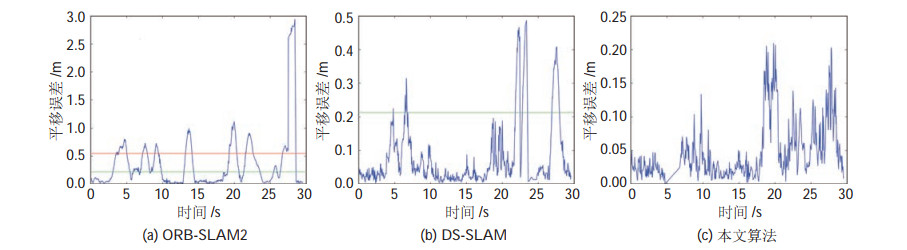
图 5为本文算法、DS-SLAM算法和ORB-SLAM2算法在“fr3/w_r”图像序列上的平移RMSE指标变化曲线，其中红色和绿色的线条分别为DS-SLAM算法和本文算法的最大偏移距离。对比(a)(b)(c) 三条曲线，ORB-SLAM2和DS-SLAM算法的相机位姿在当前序列上产生了严重的漂移，最大的平移误差达到0.98 m和0.49 m，而本文算法最大平移误差只有0.22 m，由此可见，本文算法的稳定性和鲁棒性均优于对比算法。

3.3 定位精确性检验

与视觉里程计的评估不同，SLAM系统的定位精确性与轨迹的漂移程度成负相关，即漂移程度越高，定位精度越低。因此，使用绝对轨迹误差（ATE）检测SLAM系统的定位精度。表 2对比了本文算法与ORB-SLAM2、DS-SLAM、ReFusion和无空间平面一致性SLAM算法。其中，DS-SLAM算法在对比算法中表现最好，但在“fr3/w_r”序列中，由于场景中图像存在运动模糊，因此语义分割网络识别精度降低，动态区域移除不完整，进而造成轨迹漂移严重。本文算法在“fr3/w_r”序列上，绝对轨迹误差比DS-SLAM算法降低了88%，系统精度提升明显。相比较于对比算法中精度最高的算法，本文算法在低动态环境下的绝对轨迹误差平均降低了33.4%，在高动态环境下降低了47.6%。

如图 6所示，将ORB-SLAM2算法、DS-SLAM算法和本文算法的运动轨迹和参考值之间绝对轨迹误差使用红色线段表示，红色线段长度越长，代表绝对轨迹误差越大，而本文算法的红色线段长度短于对比算法，因此，在动态图像序列上，本文算法的定位精度提升最为明显。

3.4 静态地图构建

采用本文算法和DS-SLAM算法对TUM数据集动态模糊最为严重的场景进行静态八叉树地图构建实验。

图 7(a)是DS-SLAM算法的建图结果，其中，红色线段内部区域的八叉树节点为动态地图点，而动态地图点的多少取决于语义分割网络的精度。本文算法在语义分割网络的基础上，根据动态耦合分数值对于动静态物体的处理，以及添加节点权重值$ p(\mathit{\boldsymbol{x}}) $的地图构建，实现了从平面到空间的动态地图点的移除，效果如7(b) 所示。动态物体得到了有效的剔除，进而得到较为准确的静态地图。

4 结论（Conclusion）

提出了一种基于动态耦合与空间数据关联的新型RGB-D SLAM算法。本算法利用空间数据关联将特征点法和稠密直接法作为SLAM前端来计算相机姿态，并且融入语义动态补全算法，实现对场景中语义动态物体的完整检测。在稠密直接法中，根据动态耦合分数值，获得补全后的动态物体，从而消除动态物体对位姿估计的影响。在特征点法中，采用局部BA和闭环优化线程实现了对相机姿态和地图点集的优化和更新。通过TUM数据集实验表明，本文算法在相机姿态和定位精度方面提高明显，但算法采用像素级分割网络，对计算资源占用较大，如何进一步提升运算效率，是下一步的重点。