2. 中国科学院机器人与智能制造创新研究院,辽宁 沈阳 110169;
3. 中国科学院大学,北京 100049
2. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
灾害现场废墟环境抢险救援任务紧迫,传统的轮式或履带式移动机器人难以胜任狭窄空间废墟环境救援任务[1],而蛇形机器人具备细长仿生结构和灵活多变的运动关节,更适合在狭窄空间运动[2]。现有蛇形机器人按照关节结构和运动机理可分为主动关节摩擦运动、主动关节被动轮运动、主动关节主动轮(履)运动和被动关节主动轮(履)运动4种情况[3]。实际用于灾害现场救援的蛇形机器人目前多以搜索任务为主,研究的热点集中在自适应结构设计以及自主控制方法[4-5]。由于基于摩擦运动机理的主动关节被动轮式蛇形机器人在灾难现场环境运动困难,最大推力和推进速度难以应用于实际搜救行动[6-7],因此主动轮或履带式蛇形机器人逐渐成为研究重点,这类机器人也可称作超移动机器人(hypermobile robot)[8]。例如,为了解决在狭窄和非结构化环境中进行探测的问题,日本东京工业大学广濑实验室提出了主动轮式蛇形机器人ACM-R4.1[9],该机器人每个关节集成了扭矩传感器和驱动电机,通过模块化结构解决了防尘防水、过载保护问题,提高了机器人的可维护性,但这种机器人在崎岖路面会产生打滑现象。针对此问题,广濑实验室研制了履带驱动的Souryu系列蛇形机器人[10],解决了蛇形机器人崎岖地面运动性能不足的问题,然而该系列的蛇形机器人容易倾翻。针对倾翻问题,美国密歇根大学和德国汉堡大学分别研制出履带式可重构蛇形机器人OT-4[11] 和JL-I[12],两种机器人均采用对称履带驱动结构,但都存在重量和尺寸大、不便携带的问题。综上,现有实际用于狭窄空间灾害现场的蛇形机器人功能仅限于搜索,缺少机器人化救援能力;此外功能上还不够灵活便携、环境适应能力不够强。这类机器人化装备研制难点是机器人的自适应结构设计以及机器人化救援装备集成,因为在移动平台上加装救援装备后机器人整体结构会更复杂,传统设计方法难以兼顾各模块结构对运动性能的影响,无法达到最优化设计要求[13]。由于此类设计问题具有多个待优化目标,且各目标之间往往互相矛盾,因此这类优化设计的解为Pareto最优[14]。Deb提出的基于支配关系的NSGA-II[15] 和张青富提出的基于分解的MOEA/D[16] 是两种较为成熟的进化多目标优化算法,算法可在非线性约束条件下全局搜索多维非线性目标函数的极值,且允许目标函数在目标空间离散、多峰或非凸,近年来逐渐被应用于结构优化设计领域。如Zhang等[17] 针对传统的遥控潜水器(ROV)在深海操作困难且价格昂贵的问题,设计了一种小型、可重构的履带式模块化深海探测车ROV(R-ROV)。为了获得机器人的机构参数,提出了一种考虑水下环境的R-ROV机构参数优化的方法,提高了机器人的适应性和运动性。实验表明该R-ROV可在3000 m深的海底作业,验证了基于遗传算法的多目标优化设计方法的有效性。
在对主动关节履带式蛇形机器人研究的基础之上,本文提出了一种新型的搭载有急救注射装置的主动关节履带式蛇形救援机器人,用于在废墟搜索幸存者以及执行肌肉注射操作。机器人各模块几何参数直接影响其在灾害现场危楼内部狭窄空间的机动性和能耗,由于这些性能之间存在互相制约的关系,因此片面突出某单一性能可能会导致其他性能的降低[18],进而导致急救任务的失败。为了探求最优结构参数,以机器人履带模块结构参数作为决策变量,以机器人模块的几何参数和运动过程中模块与非结构环境交互的运动学、动力学机理为约束条件,构建机器人不同环境运动性能结构参数与运动性能的数学模型。分别利用多目标遗传算法NSGA-II和MOEA/D搜索综合最优性能Pareto解,得出满足不同运动性能的机器人最优结构参数,从而指导机器人样机结构参数的设计。
2 结构设计(Structure design)鉴于灾难现场废墟环境的复杂性以及伤员急救的专业性,参考文[19] 提出的地面废墟搜救机器人通用技术条件,主动关节履带式蛇形机器人在设计时需要满足以下技术要求:
(1) 通行入口尺寸:约0.4 m(宽)
(2) 爬楼梯能力:住宅共用楼梯,最小宽度0.26 m、最大高度0.175 m。
(3) 跨越沟壑能力:沟壑宽度不小于0.3 m。
(4) 转向性能:灵活且能耗低,转向阻力矩小。
(5) 具有通过交叠瓦砾的能力。
针对上述要求,初步设计了注射急救装置以及蛇形机器人本体结构方案,为后续结构参数优化数学模型的建立以及综合性能指标与结构参数之间映射关系的构建提供分析依据。
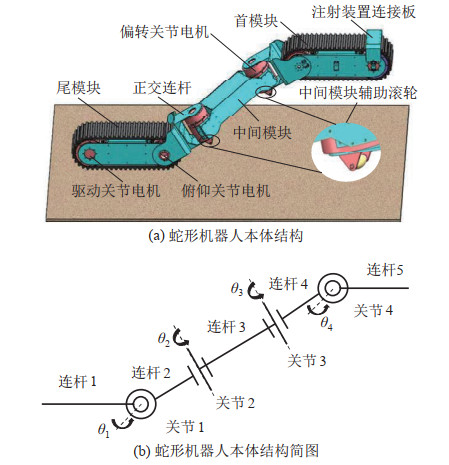
2.1 蛇形机器人本体设计蛇形救援机器人本体采用模块化设计思想,具体结构简图如图 1所示。
|
图 1 蛇形机器人本体结构简图 Fig.1 Structural sketch of the snake-like robot body |
机器人本体主要由3个模块组成,如图 1(a) 所示,其中首、尾模块采用单履带驱动,远离关节侧为驱动电机,靠近关节侧为俯仰电机。中间模块装有电源及控制系统,模块两侧为偏转电机。为了防止机器人越障时中间模块遇到“卡死”现象,在中间模块下方安装有辅助滚轮。首尾驱动模块与中间模块之间通过正交连杆连接,故关节具有俯仰和偏转2个自由度。蛇形机器人本体可用图 1(b) 结构简图表示,该结构是由5个连杆和4个旋转关节组成,其中关节1和4是俯仰关节,关节2和3是偏转关节。
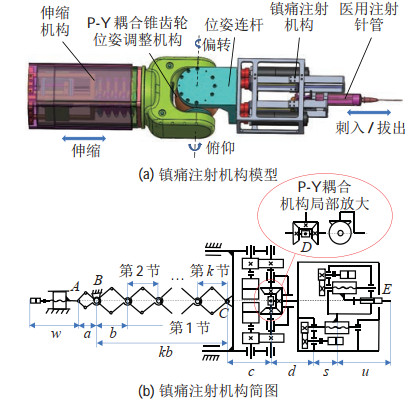
蛇形机器人在首模块上端安装有肌肉注射装置,其结构模型和机构简图如图 2所示。注射装置主要由伸缩机构、末端位姿调整机构和肌肉注射机构组成。医用注射针管内部是镇痛专用药物,注射机构主要用来确定针头末端的位姿。
|
图 2 急救注射机构结构简图 Fig.2 Structural sketch of an emergency injection mechanism |
(1) 伸缩机构
伸缩机构主要由曲柄滑块连杆机构串联而成,机构的输入是滑块的前后伸缩运动,输出是
(2) 位姿调整机构
位姿调整机构采用耦合锥齿轮结构,机构的输入是2个大扭矩舵机,利用圆柱齿轮将舵机的扭矩传动到俯仰轴两侧锥齿轮上。如图 2(b) 中P-Y耦合机构局部放大视图所示,俯仰轴上的两锥齿轮同向转动可实现偏转轴上输出锥齿轮的俯仰运动,反向转动可实现输出锥齿轮的偏转运动。输出锥齿轮轴与位姿连杆相连,将俯仰和偏转运动传递到注射机构。耦合齿轮机构中心点
(3) 注射机构
注射机构采用二级丝杠滑块结构,第1级滑块将注射针头刺入,第2级滑块将镇痛药剂推入伤员体内。利用一级圆柱齿轮将直流伺服电机动力传递到各自一级的丝杠上。针头
根据狭小废墟非结构环境机器人技术要求,蛇形救援机器人需要有非结构环境适应能力以及伤员镇痛功能。通过分析机器人构形演变机理、变结构自适应运动机理以及注射操作机理来说明机器人废墟救援功能如何实现,如图 3所示。

|
图 3 蛇形救援机器人构形演变机理与运动功能示意图 Fig.3 Configuration evolution mechanism and motion function diagrams of the snake-like rescue robot |
(1) 链式构形演变机理
本文的蛇形救援机器人采用链式结构,主要因为以下几个原因:①横截面积较小,重心低,纵向稳定性好,可通过狭小的空间;②单位地面接触面积上的接地比压小,使其能够在沼泽或者沙地等松软地面上爬行;③身体的各个部位均可与地面接触产生驱动力进行运动牵引,使得链式结构具有较强的通过能力,可以在崎岖地面上运动,也可翻越较大的沟壑、较高的垂直障碍等;④链式结构具有多于运动空间的自由度,具有较强的灵活性来实现多种步态和形态的切换来适应环境和地面。
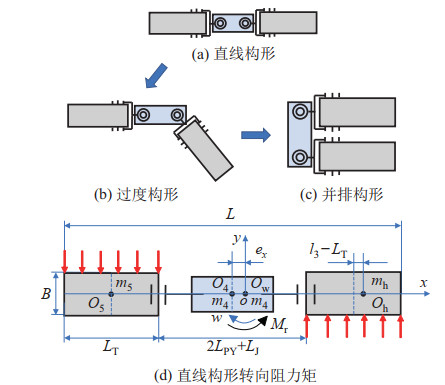
蛇形救援机器人构形有3种,分别为直线构形、过渡构形和并排构形,如图 3(a) 所示。直线构形下机器人能够通过狭窄空间、爬坡、跨越台阶和跨越沟壑,且该构形可完成肌肉注射操作,如图 3(b)(d) 所示。过渡和并排构形可分别实现铰接转向和滑移转向2种转向功能,如图 3(c) 所示。各构形之间的演变通过控制关节2、3的偏转角度(如图 1(b) 所示)来实现。
(2) 越障机理
机器人越障形式主要取决于废墟环境,根据文[19] 提出的地面废墟搜救机器人通用技术条件,机器人应能穿过狭窄空间、爬斜坡、跨沟壑、爬楼梯。考虑到废墟环境多为交叠瓦砾环境,所以机器人除了满足上述通用功能,还应该具有适应交叠瓦砾环境的能力。通过图 1(b) 所示的关节1、4的俯仰角度实现机器人的“抬头”和“弓腰”等动作,这些动作配合偏转关节2、3联合控制即可实现基本的越障功能。
(3) 转向机理
机器人的转向运动是平面直线运动和旋转运动2种运动的合成。它既与机器人的结构、动力、转向机构有关,又与地面条件有关。对于链式主动关节履带式结构,机器人主要有2种转向方式,滑移转向和铰接转向,如图 3(c) 所示。滑移转向可以实现原地360
(4) 精准注射机理
注射装置可替代救援人员实现机器人化救援操作。结合现代医学注射机理,按药物注入部位的由浅入深依次分为皮内注射、静脉注射、皮下注射以及肌肉注射。其中,肌肉注射通常是为了将药液注射到肌肉组织内,达到治病、防疫或镇痛等作用,例如疫苗注射、镇痛注射等。在机理上肌肉注射方法比皮下注射更适合地震现场废墟救援任务需求,故蛇形救援机器人的镇痛注射机构设计参考了肌肉注射。注射机构主要由伸缩机构、末端位姿调整机构和镇痛注射机构组成,整个机构的自由度为4。为了模仿医护人员拿起针头后靠近、调整和扎入的过程,机器人应该具有至少6个自由度,因此需要如图 3(d) 所示的常规镇痛和联合镇痛2种肌肉注射形式。常规镇痛,指的是在灾害现场受困者的身体与机器人处于同一平面的情况下,机器人不需要抬头、转身等动作即可将针头扎入受困者手臂肌肉中,此时机器人仅靠4个自由度调整好位置直接刺入针头即可。联合镇痛,则是指当受困人员被压在废墟交叠瓦砾下身体与机器人不处于同一平面时,机器人需要通过抬头、转身来实现注射装置和本体模块的联合控制。这时机器人的操作原理更像是以尾模块为基座的6自由度工业机器人,而注射机构则为操作手,进而实现精准注射。
3 多目标优化模型建立(Multi-objective optimization modeling)多目标优化问题一般可表示为如下数学模型[20]:
| $ \begin{align} &\min {\mathit{\boldsymbol{ F }}}(\mathit{\boldsymbol{x}})=[ f_{1}(\mathit{\boldsymbol{x}}), f_{2}(\mathit{\boldsymbol{x}}), \cdots, f_{m}(\mathit{\boldsymbol{x}})]^{\mathrm{T}}\\ &\rm {s.t.} \begin{cases} g_{i}(\mathit{\boldsymbol{x}}) \leq 0, & i= 1, \cdots, p \\ h_{j}(\mathit{\boldsymbol{x}})= 0, & j= 1, \cdots, q \\ l_{k} \leq x_{k} \leq u_{k}, & k= 1, \cdots, n \end{cases} \end{align} $ | (1) |
式中,
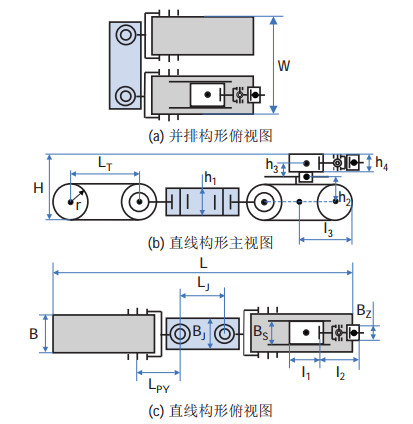
图 4为蛇形救援机器人结构参数示意图,机器人的各模块结构参数见表 1。在设计注射装置结构时,使注射装置总长
| $ \begin{align} L_{\mathrm{T}}=\min(l_{1} +l_{2}) \end{align} $ | (2) |
|
图 4 蛇形救援机器人结构参数示意图 Fig.4 Schematic diagram of the structural parameters of the snake-like rescue robot |
|
|
表 1 document Tab. 1 Table of structural parameters of the snake-like rescue robot |
| $ \begin{align} \begin{cases} l_{1}=w+a+k \beta a=(1+k \beta) a+w \\ l_{2}=s+c+d+u \end{cases} \end{align} $ | (3) |
式中
| $ \begin{align} L_{\mathrm{T}} = (1+k \beta) a_{\min }+w+c+d+u \end{align} $ | (4) |
此外注射机构质心到首模块质心的距离
| $ \begin{align} l_{3}= k \beta(a-a_{\min})+\frac{l_{2}}{2}-L_{\mathrm{T}} \end{align} $ | (5) |
联立式(3)~(5) 可得
| $ \begin{align} l_{3}&= f(a, s) \\ &= k \beta a+\frac{s}{2}-a_{\min }-\frac{c+d+u}{2}-w \end{align} $ | (6) |
可见
| $ \begin{align} \mathit{\boldsymbol{x}}= (&B, B_{\mathrm{J}}, B_{\mathrm{S}}, B_{\mathrm{Z}}, L_{\mathrm{T}}, L_{\mathrm{J}}, L_{\mathrm{PY}}, r, a, w, c, s, d, u, \\ &h_{2}, h_{3}, h_{4}, \theta_{1}, \theta_{4}) \end{align} $ | (7) |
首先根据设计经验并参考现有机器人样机,估计机器人各机构参数最优解可能出现的范围[18]。再根据设计要求以及运动性能要求,将设计变量约束条件分为几何约束和功能约束。
3.2.1 几何约束机器人几何约束是指各结构参数的初始估计范围,该范围能有效减少算法优化时间,提高效率。根据国内外现有主动关节履带式蛇形机器人样机的结构参数,给定机器人初始几何约束为
| $ \begin{align} \begin{cases} r_{\min } \leq r \leq r_{\max } , & B_{\min } \leq B \leq B_{\max } \\ B_{\mathrm{J} \min } \leq B_{\mathrm{J}} \leq B_{\mathrm{J} \max }, & B_{\mathrm{S}\min} \leq B_{\mathrm{S}} \leq B_{\mathrm{S}\max} \\ B_{\mathrm{Z} \min } \leq B_{\mathrm{Z}} \leq B_{\mathrm{Z} \max }, & L_{\mathrm{T} \min } \leq L_{\mathrm{T}} \leq L_{\mathrm{T} \max } \\ L_{\mathrm{PY} \min } \leq L_{\mathrm{PY}} \leq L_{\mathrm{PY} \max }, \kern-6pt & L_{\mathrm{J} \min } \leq L_{\mathrm{J}} \leq L_{\mathrm{J} \max } \\ h_{2 \min } \leq h_{2} \leq h_{2 \max }, & h_{3 \min } \leq h_{3} \leq h_{3 \max } \\ h_{4 \min } \leq h_{4} \leq h_{4 \max }, & \\ a_{\min } \leq a \leq a_{\max }, & w_{\min } \leq w \leq w_{\max } \\ c_{\min } \leq c \leq c_{\max }, & s_{\min } \leq s \leq s_{\max } \\ d_{\min } \leq d \leq d_{\max }, & u_{\min } \leq u \leq u_{\max } \\ \theta_{1 \min } \leq \theta_{1} \leq \theta_{1 \max }, & \theta_{4 \min } \leq \theta_{4} \leq \theta_{4 \max } \end{cases} \end{align} $ | (8) |
式中
(1) 空间通过性约束。机器人直线和并排构形下的总体几何尺寸影响着机器人的运动通过性能,因此存在几何约束
| $ \begin{align} \begin{cases} L = 2\left(L_{\mathrm{T}}+r\right)+2 L_{\mathrm{PY}}+L_{\mathrm{J}} \leq L_{\max } \\ W = B+L_{\mathrm{J}} \leq W_{\max } \\ H = r+h_{2}+h_{3}+\dfrac{h_{4}}{2} \leq H_{\max } \end{cases} \end{align} $ | (9) |
式中
(2) 质量约束。机器人依靠变形完成狭小空间自适应作业任务,各模块质量影响着机器人的变形性能,因此机器人总质量
| $ \begin{align} m_{\rm w}\le m_{\min} \end{align} $ | (10) |
根据蛇形救援机器人的设计要求,其应具有跨越台阶、沟壑以及快速稳定的转向性能,下面分别针对这些性能进行分析并建立结构参数与相应性能的目标函数。
3.3.1 跨越台阶性能在城市建筑物中,楼梯是楼层间的垂直交通枢纽,是楼房的重要构件。对履带式移动机器人而言,楼梯爬行难度随着坡度、踏步尺寸的增大而增加,合理地设计机器人的外形尺寸非常重要[21]。
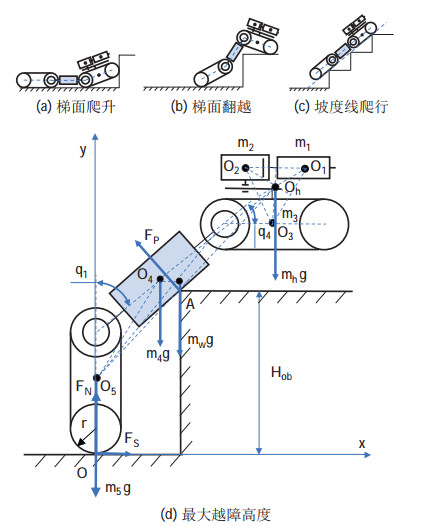
如图 5(a)~(c) 所示,机器人在楼梯上的运动过程可以分为梯面爬升、梯面翻越、坡度线爬行3个阶段。考虑机器人可作主动关节变形越障,因此这里仅分析梯面翻越过程的最大越障高度,如图 5(d) 所示。机器人可分成5个模块,将注射与位姿调整机构作为模块1,伸缩机构为模块2,机器人本体首尾驱动单元作为模块3和模块5,中间单元作为模块4。假设各模块质量均匀,质心位于几何中心,记
| $ \begin{align} \begin{cases} x_{\mathrm{m}}= \frac{1}{m_{\mathrm{w}}} \sum\limits_{i= 1}^{5} m_{i} x_{i} \\[14pt] y_{\mathrm{m}}= \frac{1}{m_{\mathrm{w}}} \sum\limits_{i= 1}^{5} m_{i} y_{i} \end{cases} \end{align} $ | (11) |
|
图 5 机器人最大越障高度分析 Fig.5 Analysis on the robot's maximum obstacle-surmounting height |
其中:
| $ \begin{align} \begin{cases} m_{1}= \rho \sigma_{1} l_{2} B_{\rm Z}\\ m_{2}= \rho \sigma_{2} l_{1} B_{\mathrm{S}} \\ m_{3}= \rho \sigma_{3} B(L_{\mathrm{T}}+2 r) \\ m_{4}= \rho \sigma_{4} B_{\mathrm{J}}(L_{\mathrm{J}}+L_{\mathrm{PY}}) \\ m_{5}= \rho \sigma_{5} B(L_{\mathrm{T}}+2 r) \\[3pt] m_{\mathrm{w}}= m_{0}+\sum\limits_{i = 1}^{5} m_{i} \end{cases} \end{align} $ | (12) |
此外,综合质量
式(11) 中
| $ \begin{align} &\left\{\begin{aligned} x_{1} & = \Big(l_{3}+\frac{L_{\mathrm{T}}}{2}\Big) \sin (\theta_{1}+\theta_{4})+ (2 L_{\mathrm{PY}}+L_{\mathrm{J}}) \sin \theta_{1} \kern -50pt \\[5pt] x_{2} & = \Big(l_{3}-\frac{l_{1}+l_{2}}{2}+\frac{L_{\mathrm{T}}}{2}\Big) \sin (\theta_{1}+\theta_{4})+ \\ &\quad (2 L_{\mathrm{PY}}+L_{\mathrm{J}}) \sin \theta_{1} \\[5pt] x_{3} & = \frac{L_{\mathrm{T}}}{2} \sin (\theta_{1}+\theta_{4})+(2 L_{\mathrm{PY}}+L_{\mathrm{J}}) \sin \theta_{1} \\[5pt] x_{4} & = \frac{(2 L_{\mathrm{PY}}+L_{\mathrm{J}}) \sin \theta_{1}}{2} \\ x_{5} & = 0 \end{aligned}\right. \end{align} $ | (13) |
| $ \begin{align} &\left\{\begin{aligned} y_{1} & = (h_{2}+h_{3}) \sin (\theta_{1}+\theta_{4})+L_{\mathrm{T}}+r+ \Big(l_{3}+\frac{L_{\mathrm{T}}}{2}\Big) \times \\ &\quad \cos (\theta_{1}+\theta_{4})+(2 L_{\mathrm{PY}}+L_{\mathrm{J}}) \cos \theta_{1} \\ y_{2} & = (h_{2}+h_{3}) \sin (\theta_{1}+\theta_{4})+L_{\mathrm{T}}+r+ \Big(l_{3}-\frac{l_{1}+l_{2}}{2}+ \\ &\quad \frac{L_{\mathrm{T}}}{2}\Big) \cos (\theta_{1}+\theta_{4})+ (2 L_{\mathrm{PY}}+L_{\mathrm{J}}) \cos \theta_{1} \\ y_{3} & = (2 L_{\mathrm{PY}}+L_{\mathrm{J}}) \cos \theta_{1}+\frac{L_{\mathrm{T}}}{2} \cos (\theta_{1}+\theta_{4})+L_{\mathrm{T}}+r \\[5pt] y_{4} & = L_{\mathrm{T}}+r+\frac{(2 L_{\mathrm{PY}}+L_{\mathrm{J}}) \cos \theta_{1}}{2} \\[5pt] y_{5} & = \frac{L_{\mathrm{T}}}{2}+r \end{aligned}\right. \end{align} $ | (14) |
当机器人整体重心
| $ \begin{align} H_{\mathrm{ob}}= \frac{F_{\mathrm{N}} x_{\mathrm{m}}}{F_{\mathrm{S}}}= \frac{x_{\mathrm{m}}}{\mu_{x}} \end{align} $ | (15) |
式中
此外,根据几何分析可得到障碍的最大高度为
| $ \begin{align} H_{\mathrm{ob}}= x_{\mathrm{m}} \cot \theta_{1}+L_{\mathrm{T}}+r-\frac{r}{\sin \theta_{1}} \end{align} $ | (16) |
联立式(11)~(16) 可得到当障碍达到可跨越的最大高度时,越障中的机器人尾模块俯仰关节角
| $ \begin{align} \min f_{1}(\mathit{\boldsymbol{x}})= \frac{1}{H_{\mathrm{ob}}} \end{align} $ | (17) |
沟壑跨越爬行有动力爬行和静力爬行2种方式,其中动力爬行多用于高速形式的装甲车辆。考虑到蛇形救援机器人的运动速度和加速度通常较小,这里仅考虑静力爬行。按照沟壑障碍坡度可以将沟壑分为平地沟壑和斜面沟壑2种,如图 6(a)(b) 所示,图中
| $ \begin{align} W_{\mathrm{ob}}= \min \{x_{\mathrm{m}}, L-x_{\mathrm{m}}\} \end{align} $ | (18) |

|
图 6 机器人最大越障宽度分析 Fig.6 Analysis on the robot's maximum obstacle-surmounting width |
因此,蛇形救援机器人跨越沟壑性能的目标函数为
| $ \begin{align} \min f_{2}(\mathit{\boldsymbol{x}}) = \frac{1}{W_{\mathrm{ob}}} \end{align} $ | (19) |
常健等[22] 针对废墟狭小环境中可变形机器人AMOEBA-I在直线构形下难以进行转向的问题提出了评价链式履带可变形机器人转向性能优劣的指标,其本质是对AMOEBA-I直线构形的转向过程中各项性能的线性加权。对于本文设计的蛇形救援机器人,其转向构形为直线构形和并排构形。如图 7(a)~(c) 所示,机器人从直线构形到并排构形需要改变图 1(b) 中偏转关节的偏转角度
|
图 7 机器人直线构形转向阻力矩分析 Fig.7 Analysis on the steering resistance torque of robot in the linear configuration |
以机器人整体重心
| $ \begin{align} &m_{5} \left(\frac{L_{\mathrm{T}}+2 L_{\mathrm{PY}}+L_{\mathrm{J}}}{2}+e_{x}\right)+m_{4} e_{x} \\ =&m_{\mathrm{h}} \left(\frac{2 L_{\mathrm{PY}}+L_{\mathrm{J}}+L_{\mathrm{T}}}{2}-e_{x}+l_{3}-L_{\mathrm{T}}\right) \end{align} $ | (20) |
联立式(6)(20) 可求出机器人直线构形下转向的接地比压中心偏移为
| $ \begin{align} e_{x}= &\frac{1}{m_{5}+m_{4}+m_{\mathrm{h}}} \Big(\frac{m_{\mathrm{h}}-m_{5}}{2} L_{\mathrm{J}}+\\ &(m_{\mathrm{h}}-m_{5}) L_{\mathrm{PY}}-\frac{m_{\mathrm{h}}+m_{5}}{2} L_{\mathrm{T}}+\\ &m_{\mathrm{h}} \Big(k \beta a+\frac{1}{2} s-a_{\min }-\frac{c+d+u}{2}-w\Big)\Big) \end{align} $ | (21) |
因此,机器人直线构形下转向阻力矩为
| $ \begin{align} M_{\mathrm{r}}= \int_{-l_{4}}^{-l_{5}} \mu_{y} \frac{m_{5} g}{L_{\mathrm{T}}} x \mathrm{ d} x+\int_{+l_{6}}^{+l_7} \mu_{y} \frac{m_{\mathrm{h}} g}{L_{\mathrm{T}}} x \mathrm{ d} x \end{align} $ | (22) |
式中,积分上下限
| $ \begin{align} \begin{cases} l_{4}= \dfrac{1}{2}(2 L_{\mathrm{PY}}+L_{\mathrm{J}})+e_{x}+L_{\mathrm{T}} \\[9pt] l_{5}= \dfrac{1}{2}(2 L_{\mathrm{PY}}+L_{\mathrm{J}})+e_{x} \\[9pt] l_{6}= \dfrac{1}{2}(2 L_{\mathrm{PY}}+L_{\mathrm{J}})-e_{x} \\[9pt] l_{7}= \dfrac{1}{2}(2 L_{\mathrm{PY}}+L_{\mathrm{J}})-e_{x}+L_{\mathrm{T}} \end{cases} \end{align} $ | (23) |
联立式(22)(23) 可求出机器人直线构形转向阻力矩为
| $ \begin{align} M_{\mathrm{r}}= & \frac{\mu_{y} g}{2}(L_{\mathrm{T}}+2 L_{\mathrm{PY}}+L_{\mathrm{J}})(m_{5}+m_{\mathrm{h}})+ \\ &\mu_{y} g(m_{5}-m_{\mathrm{h}}) e_{x} \end{align} $ | (24) |
式中
由于机器人转向阻力矩影响着机器人驱动电机的最小输出力矩,因此,机器人的转向性能目标函数为
| $ \begin{align} \min f_{3}({\mathit{\boldsymbol{ x }}})= M_{\mathrm{r}} \end{align} $ | (25) |
基于第3节建立的多目标优化模型,利用文[23] 多目标优化平台PlatEMO,笔者对蛇形机器人结构参数优化问题进行多目标优化。PlatEMO版本是v3.2,Matlab版本是R2020b。首先在求解之前给出各设计变量和约束条件的范围,如表 2所示。
|
|
表 2 变量及其约束条件 Tab. 2 Variables and their constraint conditions |
此外,还需要给出非优化结构参数和相关常量的取值,如表 3所示。
|
|
表 3 非优化结构参数(常量取值) Tab. 3 Non-optimized structural parameters (constant values) |
本文使用的计算机配置为CPU:R7-4800H,GPU:RTX2060,内存16G。种群大小
对于NSGA-II算法,编码方式为实数编码,适应度评价函数为

|
图 8 NSGA-II优化结果图 Fig.8 NSGA-II optimization result |
对于MOEA-D算法,编码方式为实数编码,通过二层边界交叉方法生成权重向量,采用基于惩罚的边界交叉方法生成种群解,惩罚因子取为5。优化结果如图 9所示。
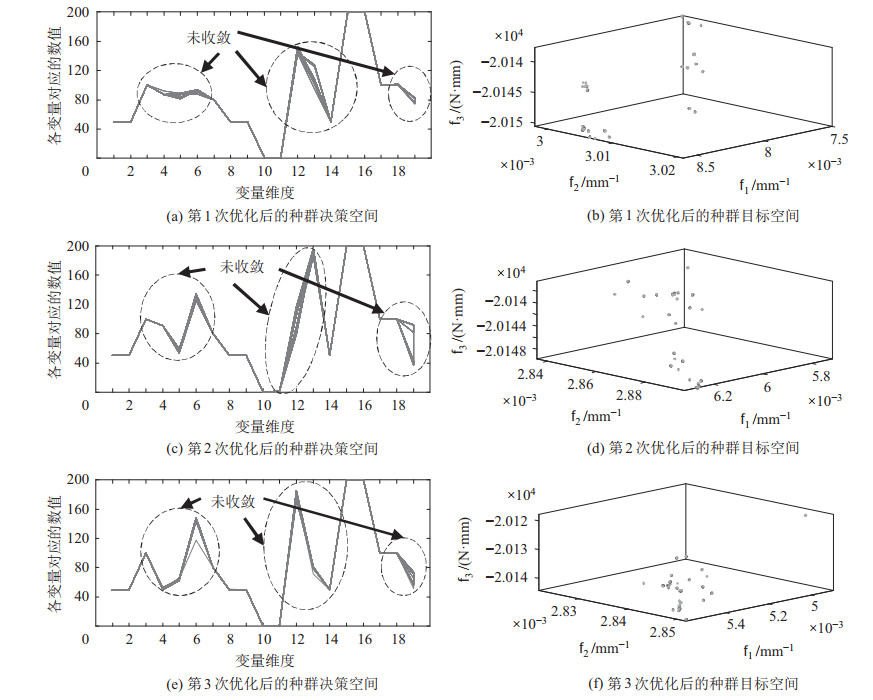
|
图 9 MOEA-D优化结果图 Fig.9 MOEA-D optimization result |
从图 8可看出,种群大小为100的群体,在10 000次进化后,前2次优化中每个决策变量都收敛,仅在第3次优化中存在1处未收敛的部分。可见NSGA-II算法在求解本文的多目标模型时大概率有效。利用NSGA-II算法求解时平均计算时间为0.747 s。3次运算总共获得273个最优解。
从图 9可以看出,种群大小为100的群体,在10 000次进化后,3次优化设计变量最终都存在3处明显的不收敛现象,主要集中在第5、6、12、13、19个设计变量的多解情况。因此MOEA-D算法在求解模型上存在少数设计变量无法收敛情况,难以胜任本文的多目标优化模型。此外,利用NSGA-II算法求解的平均计算时间为1.9 s。3次运算总共获得82个最优解。
通过对比NSGA-II和MOEA-D(图 8和图 9)两种算法的求解结果可知,NSGA-II算法能够有效求解本文建立的多目标优化模型,且在运算时间上较MOEA-D算法更短。
考虑到NSGA-II算法的优化结果有273个Pareto集,MOEA-D算法的优化结果有82个Pareto集,为了从中优选出一个最优解,这里采用平均值法处理相应的数据。优化结果如表 4和表 5所示。通过对比可知,利用NSGA-II算法优化的蛇形救援机器人结构参数在越障高度
|
|
表 4 NSGA-II算法优化结果表 Tab. 4 Table of NSGA-II optimization result |
|
|
表 5 MOEA-D算法优化结果表 Tab. 5 Table of MOEA-D optimization result |
为了验证NSGA-II算法的优化结果(表 4)是否满足第2节讨论的蛇形救援机器人技术要求,按照最优结构参数研制机器人样机,理论上机器人最大跨越台阶高度
为了验证机器人样机的台阶翻越性能,搭建如图 10所示的机器人越障高度测定试验平台。利用红砖搭建机器人台阶越障高度实验场地,改变实验用红砖尺寸进而改变总体障碍的高度。如图 10所示,机器人爬台阶过程主要有4个阶段:(1) 靠近台阶后抬头,便于搭上梯面与踏面交界线;(2) 低头后弓腰爬上台阶;(3) 首尾模块同时驱动,让尾模块靠近台阶;(4) 尾模块搭上台阶梯面与踏面边界后抬起,完成翻越。重复上述(1)~(4) 爬台阶过程6次,实验结果表明,当4块红砖尺寸均为210 mm

|
图 10 机器人台阶翻越高度实验 Fig.10 Experiment on the step surmounting height of the robot |
蛇形救援机器人在废墟环境中,除了会遇到斜坡、楼梯、台阶等结构化环境,还会遇到沟壑、狭窄入口交叠瓦砾等非结构环境。为了验证蛇形救援机器人样机的跨越沟壑能力,利用红砖搭建实验场地,如图 11所示。

|
图 11 机器人沟壑跨越宽度实验 Fig.11 Experiment on the gully crossing width of the robot |
实验中通过改变沟壑近端和远端之间的红砖距离进而改变沟壑宽度。如图 11所示,机器人样机采用直线构形完成整个沟壑跨越过程。该过程可分为2个阶段:(1) 机器人首尾模块驱动其向前推进,在靠近沟壑近端时降低速度,并在始终保持构形不变的条件下首模块跨出沟壑近端并搭上沟壑远端;(2) 继续保持原有姿态和运动状态,当尾模块也跨出沟壑近端并搭上沟壑远端时,继续前进即可顺利跨越沟壑。重复上述(1)(2) 跨越沟壑过程6次,实验结果表明,当沟壑宽度为0.4 m时达到机器人沟壑跨越极限。因此,机器人跨越沟壑最大宽度的实验值为0.4 m,优于优化后的理论计算结果。理论上,如果机器人整体质量分布均匀,机器人可以跨越小于自身长度一半的沟壑。但是,对于本文的主动关节履带式蛇形机器人,机器人各模块之间利用俯仰和偏转关节电机相连,当首模块重心离开沟壑近端时,机器人整体可等效为悬臂梁结构。此时关节伸出部分将产生较大的挠度,从而对于机器人整体结构造成较大的压力而导致重心偏移。所以,一般情况下,为保护关节电机和机器人的连接构件,该型机器人所能跨越的沟壑宽度应小于理论值,即小于
| $ \begin{align*} E_{\rm{r沟}} =\dfrac{W_{{\rm{ob实}}} -W_{{\rm{ob}}}} {W_{{\rm{ob实}}}} \times 100\% =2.3\% \end{align*} $ |
根据式(24),在直线构形下蛇形救援机器人转向时的地面阻力矩主要取决于系统质量、履带接地面长度和地面摩擦系数等。首先搭建直线构形转向阻力矩测定实验平台,如图 12所示。
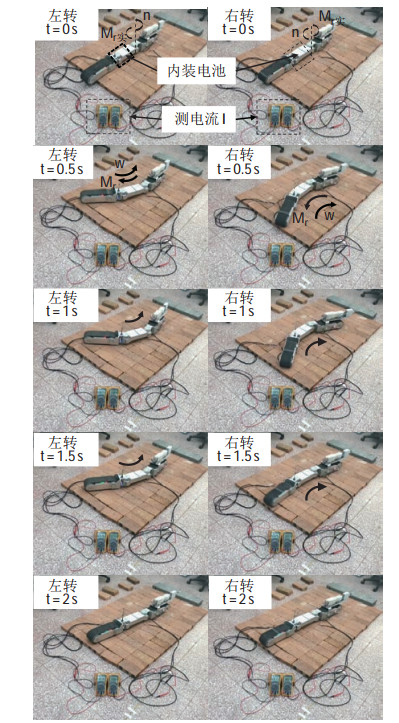
|
图 12 机器人转向阻力矩测定实验截图 Fig.12 Experiment snapshots of measuring the steering resistance torque of the robot |
当机器人在直线构形下想要以
| $ \begin{align*} E_{\rm{r转}} =\dfrac{M_{\rm{r实}} -M_{\rm r}} {M_{\rm{r实}}} \times 100\% =11.2\% \end{align*} $ |
|
|
表 6 机器人转向阻力矩测定实验记录 Tab. 6 Experimental record of measuring the steering resistance torque of the robot |
通过5.1~5.3节的实验,得到了蛇形救援机器人样机的台阶翻越高度、沟壑跨越宽度、直线构形转向阻力矩等性能指标。为了更直观地展现其性能特点,将国内外现有的相同模块数且驱动方式相似的蛇形机器人与本文的蛇形救援机器人进行比较,如表 7所示,数据取自文[2, 8]。通过表 7可以看出,本文的搭载注射装置的蛇形机器人最大越障高度较其他机器人小,但具有更快的行进速度和较小的截面尺寸,更适合快速通过窄入口。
|
|
表 7 现有蛇形机器人与本文样机性能对比表 Tab. 7 Performances comparison between the existing snake-like robots and the prototype in this paper |
在对现有地震灾害救援机器人样机结构和性能开展研究的基础上,设计了一种带有急救注射功能的主动关节履带式蛇形机器人。在结构设计之初建立机器人各模块结构参数和废墟运动性能之间的函数关系,利用多目标遗传算法NSGA-II和MOEA-D搜索函数的全局最优值,通过优化结果可知NSGA-II算法在搜索效果上明显优于MOEA-D算法。根据优化结果研制机器人样机,并通过实验验证机器人台阶越障高度、沟壑越障宽度、直线构形平地转向阻力矩等性能,结果表明基于NSGA-II优化的多目标遗传算法在求解机器人的结构参数上具有可行性,可用于指导机器人结构设计。
后续的研究工作主要有:(1) 针对NSGA-II算法在收敛性上的不足,探究适合3维甚至更高维目标函数的多目标求解算法,使优化结果更接近真实情况;(2) 继续研究机器人样机的楼梯越障性能、爬坡越障性能和防倾翻稳定性能,同时优化机器人结构参数,探求机器人最优结构参数设计方法;(3) 建模时考虑废墟环境存在的干扰,如地震余震、管道漏水湿滑、废墟瓦砾松动等对机器人运动的影响。
| [1] |
董炳艳, 张自强, 徐兰军, 等. 智能应急救援装备研究现状与发展趋势[J]. 机械工程学报, 2020, 56(11): 1-25. Dong B Y, Zhang Z Q, Xu L J, et al. Research status and development trend of intelligent emergency rescue equipment[J]. Journal of Mechanical Engineering, 2020, 56(11): 1-25. |
| [2] |
Murphy R R, Tadokoro S, Kleiner A. Disaster robotics[M]// Springer Handbooks. Berlin, Germany: Springer, 2016: 1577-1604.
|
| [3] |
Liu J D, Tong Y C, Liu J G. Review of snake robots in constrained environments[J]. Robotics and Autonomous Systems, 2021, 141. DOI:10.1016/j.robot.2021.103785 |
| [4] |
张丹凤. 基于路径边沿引导策略的蛇形机器人路径跟踪方法[J]. 机器人, 2021, 43(1): 36-43. Zhang D F. A path tracking method for the snake robot based on the path edge guidance strategy[J]. Robot, 2021, 43(1): 36-43. |
| [5] |
Pransky J. The Pransky interview: Dr Howie Choset, CTO, advanced robotics for manufacturing institute; Professor, Carnegie Mellon; Snake robotics inventor and entrepreneur[J]. Industrial Robot, 2017, 44(5): 571-574. DOI:10.1108/IR-06-2017-0113 |
| [6] |
Tang W B, Ma S G. Analysis of rectilinear motion of a threesegment snake robot under action of dry friction[C]//IEEE International Conference on Robotics and Automation. Piscataway, USA: IEEE, 2015: 3723-3728.
|
| [7] |
Ariizumi R, Matsuno F. Dynamic analysis of three snake robot gaits[J]. IEEE Transactions on Robotics, 2017, 33(5): 1075-1087. DOI:10.1109/TRO.2017.2704581 |
| [8] |
Granosik G. Hypermobile robots – The survey[J]. Journal of Intelligent & Robotic Systems, 2014, 75: 147-169. |
| [9] |
Takaoka S, Yamada H, Hirose S. Snake-like active wheel robot ACM-R4.1 with joint torque sensor and limiter[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2011: 1081-1086.
|
| [10] |
Suzuki K, Nakano A, Endo G, et al. Development of multiwheeled snake-like rescue robots with active elastic trunk[C]// IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2012: 4602-4607.
|
| [11] |
Borenstein J, Hansen M, Borrell A. The OmniTread OT-4 serpentine robot – Design and performance[J]. Journal of Field Robotics, 2007, 24(7): 601-621. DOI:10.1002/rob.20196 |
| [12] |
Zhang H, Wang W, Deng Z, et al. A novel reconfigurable robot for urban search and rescue[J]. International Journal of Advanced Robotic Systems, 2006, 3(4): 359-366. |
| [13] |
Kim J, Kim J, Lee D. Mobile robot with passively articulated driving tracks for high terrainability and maneuverability on unstructured rough terrain: Design, analysis, and performance evaluation[J]. Journal of Mechanical Science and Technology, 2018, 32: 5389-5400. DOI:10.1007/s12206-018-1037-4 |
| [14] |
宁伟康. 进化多目标优化算法研究及其应用[D]. 西安: 西安电子科技大学, 2018. Ning W K. Research on evolutionary multi-objective optimization algorithm and its application[D]. Xi'an: Xidian University, 2018. |
| [15] |
Deb K, Pratap A, Agarwal S, et al. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ[J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197. |
| [16] |
Zhang Q F, Li H. MOEA/D: A multiobjective evolutionary algorithm based on decomposition[J]. IEEE Transactions on Evolutionary Computation, 2007, 11(6): 712-731. DOI:10.1109/TEVC.2007.892759 |
| [17] |
Zhang Y X, Zhang Q F, Zhang A Q, et al. Mechanismparameters optimization of a reconfigurable tracked mobile modular deep-sea rover ROV[C]//OCEANS. Piscataway, USA: IEEE, 2018. DOI: 10.1109/OCEANSKOBE.2018.8559331.
|
| [18] |
Li N, Ma S G, Wang M H, et al. An optimization design method for the mechanism parameters of an amphibious transformable robot[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2012: 2282-2288.
|
| [19] |
国家市场监督管理总局, 中国国家标准化管理委员会. 地面废墟搜救机器人通用技术条件: GB/T 37703-2019[S]. 北京: 中国标准出版社, 2019. State Administration for Market Regulation, Standardization Administration. General specifications of ground robots for search and rescue in ruins: GB/T 37703-2019[S]. Beijing: Standards Press of China, 2019. |
| [20] |
郑金华, 邹娟. 多目标进化优化[M]. 北京: 科学出版社, 2017. Zheng J H, Zou J. Multi-objective evolutionary optimization[M]. Beijing: Science Press, 2017. |
| [21] |
朱岩, 王明辉, 李斌, 等. 履带可变形机器人越障性能研究[J]. 机器人, 2015, 37(6): 693-701. Zhu Y, Wang M H, Li B, et al. On obstacle-surmounting performance for a transformable tracked robot[J]. Robot, 2015, 37(6): 693-701. |
| [22] |
常健, 吴成东, 李斌. 可变形机器人直线构形滑移转向方法[J]. 机械工程学报, 2012, 48(7): 9-15. Chang J, Wu C D, Li B. Shape-shifting robot skid-turning with line configuration[J]. Journal of Mechanical Engineering, 2012, 48(7): 9-15. |
| [23] |
Tian Y, Cheng R, Zhang X Y, et al. PlatEMO: A Matlab platform for evolutionary multi-objective optimization[J]. IEEE Computational Intelligence Magazine, 2017, 12(4): 73-87. |
 2022, Vol. 44
2022, Vol. 44


