2. 中国北方车辆研究所,北京 100072
2. China North Vehicle Research Institute, Beijing 100072, China
自然界中的许多动物能在崎岖复杂的环境中高效运动,比如:猎豹能在草原上急速奔跑;岩羊能在乱石间自由穿梭,也能攀登悬崖峭壁。动物的运动机理对机器人设计具有很大的启发作用,从仿生学角度设计出像动物般运动灵活、适应性强的四足仿生机器人,一直是机器人领域的研究热点。
很多生物学家对四足动物的奔跑运动进行研究以探索动物高速运动的机理。如Hildebrand[1-2] 对马和猎豹的奔跑影像资料进行对比分析,发现猎豹在高速奔跑时步幅可达腿长的8.5 ~11.5倍或身长的5.25~6.25倍,而马的步幅仅为腿长的4.5~5倍或身长的3.5~4倍;猎豹奔跑时脊柱会发生大幅的屈伸运动,而马的脊柱的运动幅度明显小于猎豹。由此,他提出脊柱运动对动物高速奔跑具有重要作用。类似的,Gambaryan[3] 通过分析5种小型哺乳动物自由奔跑时的影像,发现脊柱与腿部的运动存在严格的协调关系,脊柱的弯曲及伸展极限发生在后腿触地前及离地后的极短的时间内。Schilling[4] 还提出动物骨盆的运动主要依靠脊柱的运动而产生的观点。Alexander[5] 通过对鹿和灰狗的解剖,分析其躯干肌肉、肌腱以及脊椎的力学性能,发现鹿在奔跑时躯干弯曲会储存约50% 的能量,灰狗的这一数值更是达到了70%,进而提出四足动物在奔跑时会发生腿部动能与背部势能相互转化的观点。Gray[6] 发现猎豹在高速奔跑时腿部肌肉不足以提供足够的爆发能量,而背部肌肉的收缩会产生强大的机械力来增强腿部的力量,以满足动物高速奔跑时的巨大能量需求。这些生物学方面的研究都表明:脊柱无论从运动学还是力学上对于动物奔跑都具有极其重要的作用。
目前世界上知名的四足机器人研究更关注腿部的结构设计,而忽略了脊柱对运动的作用,如意大利技术研究院的HyQ[7]、HyQ2 Max[8],苏黎世联邦理工学院的ANYmal[9],MIT(麻省理工学院)的Cheetah 2[10]、Cheetah 3[11]、Cheetah Mini[12],波士顿动力公司的Spot、SpotMini[13],山东大学的SCalf[14-15],宇树科技公司的Laikago[16]、Aliengo[17],杭州云深处科技公司的“绝影”[18] 等。这些机器人尽管能够实现稳定运动,但运动速度与其仿生对象相比仍有很大差距。国内外也有一些包含脊柱的四足机器人,如波士顿动力公司的液压机器人Cheetah,躯干含有一个主动铰接式关节,在跑步机上奔跑速度可达48 km/h,而它的“无缆版”四足机器人WildCat含有三段式液压驱动主动脊柱,室外奔跑速度可达32 km/h[13]。MIT的Kim团队[19-20] 的Cheetah 1四足机器人,含有模仿动物脊柱设计的差分驱动式脊柱,由刚性的椎骨和环状聚氨酯橡胶制成的柔性椎间盘串联,通过钢丝绳将脊柱运动与后腿运动差分耦合,实现了22 km/h的奔跑速度。瑞士苏黎世大学的赵倩等[21] 设计了由气动肌肉驱动的9自由度四足机器人Renny,研究了脊柱形态以及脊柱—腿部的协调关系对四足机器人奔跑性能的影响。本课题组之前也设计了一款四叶草变刚度被动脊柱,由弹性模量较大的ABS工程塑料制成的椎骨与弹性模量较小的聚氨酯弹性体制成的椎间盘经由钢丝绳串联而成,通过调节钢丝绳张紧程度来改变脊柱的刚度,实验发现脊柱刚度对机器人运动效果具有调节作用[22]。
脊柱运动与腿部运动的协调也是一个需要解决的重要问题。MIT的Kim团队[19] 开发的Cheetah 1机器人通过被动机构实现脊柱与腿运动的耦合;上海交通大学的王石刚等[23] 使用线性函数主动控制脊柱运动,实现了机器人的稳定运动;华中科技大学聂华[24] 使用近似正弦函数控制脊柱运动;本课题组曾采用CPG(中枢模式发生器)神经元振荡器将脊柱的运动与腿部运动进行耦合,实现了机器人的稳定运动[25]。这些控制方法虽然实现了脊柱的主动控制,但是对四足机器人整体动力学特性以及脊柱运动轨迹的动力学影响考虑不足,无法解释或证明脊柱对高速运动的重要作用。
本文根据仿生学原理设计了四足机器人的铰接式仿生脊柱,分析了仿生脊柱对于提高机器人运动速度的作用机理。
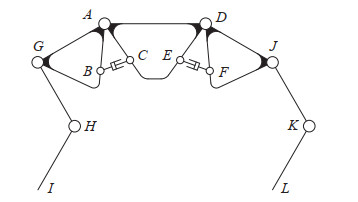
2 仿猎豹四足机器人机构设计(Mechanism design of a cheetah-mimicking quadruped robot)猎豹高速运动时的骨骼形态见图 1,可见猎豹的脊柱在奔跑时具有明显的屈伸运动。脊柱由大量椎骨组成,椎骨通过多组肌肉驱动实现整体屈伸运动。脊柱的复杂结构使其神经控制非常复杂,如果直接按照脊柱形态进行四足机器人脊柱的仿生设计,将导致机器人的控制系统过于复杂,不适合高速奔跑运动。因此,本文对脊柱进行分区简化,根据运动灵活度,将脊柱划分为胸、腹、髋3个区域,胸、腹之间设计一个俯仰方向胸关节,腹、髋之间设计一个俯仰方向腰关节,由此构成三段铰接式躯干。胸关节和腰关节通过四杆机构实现主动控制,由液压缸驱动,通过改变胸部和髋部相对于腹部的姿态来模仿动物脊柱的屈伸运动。机器人每条腿有髋关节和膝关节2个俯仰自由度,结构如图 2所示,各部分具体参数见表 1。

|
图 1 猎豹奔跑时的骨骼形态图 Fig.1 Skeletal morphology of a running cheetah |
|
图 2 仿猎豹四足机器人机构 Fig.2 Mechanism of a cheetah-mimicking quadruped robot |
|
|
表 1 四足机器人物理参数 Tab. 1 Physical parameters of the quadruped robot |
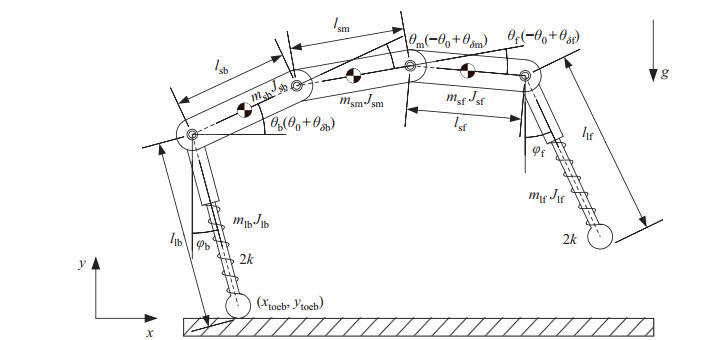
四足机器人奔跑时腿部采用跳跃步态,为了研究脊柱关节对腿部的动力学影响以及脊柱驱动力矩的变化规律,对四足机器人进行动力学建模。见图 3,将机器人前后腿分别简化为一根弹簧杆[26],建立后腿触地状态下的机构模型,运动方向为
|
图 3 机器人跳跃步态后腿触地状态 Fig.3 The stance state of hind legs of robot in bound gait |
设定机器人各构件为杆模型,各杆质心位于几何中心,采用拉格朗日方法进行动力学建模。如图 3所示,当机器人以跳跃步态奔跑时,后腿触地瞬间,前腿腾空,前腿弹簧处于初始长度,四足机器人运动状态由
| $ \begin{align} \mathit{\boldsymbol{q}}=[l_{{\rm{lb}}}, \varphi_{\rm b}, \theta_{{\rm{ \delta b}}}, \theta_{{\rm{ \delta m}}}, \theta_{{\rm{ \delta f}}}, \varphi_{\rm f}]^{\rm T} \end{align} $ | (1) |
在世界坐标系中描述各杆质心的位置,其中,后腿质心坐标值为
| $ \begin{align} \begin{cases} {x_{{\rm{lb}}} =x_{{\rm{toeb}}} -\dfrac{1}{2}l_{{\rm{lb}}} \sin \varphi_{\rm b}} \\ {y_{{\rm{lb}}} =\dfrac{1}{2}l_{{\rm{lb}}} \cos \varphi_{\rm b}} \end{cases} \end{align} $ | (2) |
髋部质心坐标值为
| $ \begin{align} \begin{cases} {x_{{\rm{sb}}} =x_{{\rm{toeb}}} -l_{{\rm{lb}}} \sin \varphi_{\rm b} +\dfrac{1}{2}l_{{\rm{sb}}} \cos \theta_{\rm b}} \\ {y_{{\rm{sb}}} =l_{{\rm{lb}}} \cos \varphi_{\rm b} +\dfrac{1}{2}l_{{\rm{sb}}} \sin \theta_{\rm b}} \end{cases} \end{align} $ | (3) |
同样,得到腹部质心位置
| $ \begin{align} E_{{\rm k} i} =\frac{1}{2}m_{i} (\dot{x}_{i}^{2} +\dot{y}_{i}^{2})+\frac{1}{2}J_{i} \omega_{i}^{2} \end{align} $ | (4) |
式中,
各杆势能由式(5) 求得,其中,后腿由于弹簧的存在,还含有弹性势能:
| $ \begin{align} E_{{\rm p} i} =\begin{cases} {m_{i} gy_{i}}, & i={\rm{lf, sf, sm, sb}} \\ {m_{i} gy_{i} +\dfrac{1}{2}(2k)(l_{0} -l_{i})^{2}}, & i={\rm{lb}} \end{cases} \end{align} $ | (5) |
根据拉格朗日方程(6) 求得各关节力矩:
| $ \begin{align} \tau_{i} =\frac{\rm d}{{\rm d}t}(\frac{\partial L}{\partial \dot{q}_{i}})-\frac{\partial L}{\partial q_{i}}, \quad i=1, 2, \cdots, 6 \end{align} $ | (6) |
其中
| $ \begin{align} \begin{bmatrix} \tau_{l_{{\rm{lb}}}} \\ \tau_{\varphi_{\rm b}} \\ \tau_{\theta_{{\rm{ \delta b}}}} \\ \tau_{\theta_{{\rm{ \delta m}}}} \\ \tau_{\theta_{{\rm{ \delta f}}}} \\ \tau_{\varphi_{\rm f}} \end{bmatrix}\!\!\!= \;& \mathit{\boldsymbol{M}}(q)\begin{bmatrix} \ddot{l}_{{\rm{lb}}} \\ \ddot{\varphi}_{\rm b} \\ \ddot{\theta}_{{\rm{ \delta b}}} \\ \ddot{\theta}_{{\rm{ \delta m}}} \\ \ddot{\theta}_{{\rm{ \delta f}}} \\ \ddot{\varphi}_{\rm f} \end{bmatrix}\!\!\!+\!\mathit{\boldsymbol{C}}(q)\!\!\begin{bmatrix} \dot{l}_{{\rm{lb}}}^{2} \\ \dot{\varphi}_{\rm b}^{2} \\ \dot{\theta}_{{\rm{ \delta b}}}^{2} \\ \dot{\theta}_{{\rm{ \delta m}}}^{2} \\ \dot{\theta}_{{\rm{ \delta f}}}^{2} \\ \dot{\varphi}_{\rm f}^{2} \end{bmatrix}\!\!\!+\!\mathit{\boldsymbol{B}}(q)\!\!\begin{bmatrix} \dot{l}_{{\rm{lb}}} \dot{\varphi}_{\rm b} \\ \dot{\theta}_{{\rm{ \delta b}}} \dot{\theta}_{{\rm{ \delta m}}} \\ \dot{\theta}_{{\rm{ \delta b}}} \dot{\theta}_{{\rm{ \delta f}}} \\ \dot{\theta}_{{\rm{ \delta b}}} \dot{\varphi}_{\rm f} \\ \dot{\theta}_{{\rm{ \delta m}}} \dot{\theta}_{{\rm{ \delta f}}} \\ \dot{\theta}_{{\rm{ \delta m}}} \dot{\varphi}_{\rm f} \\ \dot{\theta}_{{\rm{ \delta f}}} \dot{\varphi}_{\rm f} \end{bmatrix}\!\!\!+ \\ & \mathit{\boldsymbol{G}}(q) \end{align} $ | (7) |
式中,
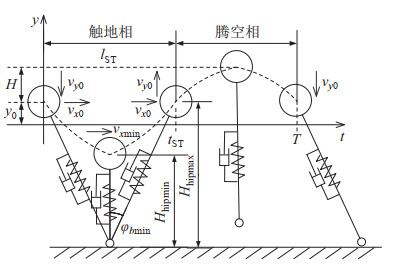
将四足机器人的腿简化为带弹簧和阻尼的虚拟腿,在Raibert提出的SLIP模型[27-28] 的基础上,建立带阻尼的SLIP模型(D-SLIP),分析四足机器人的奔跑运动过程,如图 4所示。
|
图 4 触地相虚拟腿运动过程 Fig.4 The virtual leg movement process in stance phase |
对图 4中D-SLIP模型在竖直方向的运动进行分析,等同于质量为
| $ \begin{align} y(t)=A{\rm e}^{-\zeta \omega_{\rm n} t}\cos (\omega_{\rm d} t+\varphi) \end{align} $ | (8) |
式中,
弹簧力为
| $ \begin{align} F_{\rm ST} (t)=ky_{0} -ky-C\dot{y} \end{align} $ | (9) |
式中
| $ \begin{align} ky_{0} -Cv_{y\max} =mg \end{align} $ | (10) |
式中
当
| $ \begin{align} y_{0} &=y(0) \end{align} $ | (11) |
| $ \begin{align} v_{y0} &=\dot{y}(0) \end{align} $ | (12) |
当小球加速度为0时,速度达到最大,有:
| $ \begin{align} y(t)=0 \end{align} $ | (13) |
当
| $ \begin{align} v_{y\max} =A{\rm e}^{-\zeta \omega_{\rm n} t}\sqrt{(\zeta \omega_{\rm n})^{2}+\omega_{\rm d}^{2}} \end{align} $ | (14) |
联立式(9)~(14) 可求得弹簧振动曲线参数
图 4中腾空相小球做加速度为
| $ \begin{align} \int_0^{t_{\rm ST}} {F_{\rm ST}} {\rm d}t+m( {-\dot{y}(0)-\dot{y}(t_{\rm ST})})=mgT \end{align} $ | (15) |
式中
采用抛物线近似描述水平方向上小球速度的变化过程:
| $ \begin{align} \dot{x}(t)=at^{2}+c \end{align} $ | (16) |
式中
当
| $ \begin{align} \begin{cases} \dot{x}(t)=v_{x0} \\ x=l_{\rm ST} \end{cases} \end{align} $ | (17) |
式中
设机器人的最大奔跑速度为
| $ \begin{align} l_{\rm ST} =v_{\max} t_{\rm ST} \end{align} $ | (18) |
联立式(16)~(18) 可解得小球水平方向上的运动轨迹
由此可求得四足机器人腿长随时间的变化为
| $ \begin{align} l_{{\rm{lb}}} =H_{{{\rm{hip}}}\min} +y_{0} -y \end{align} $ | (19) |
四足机器人腿的摆动幅值为虚拟腿与竖直方向的夹角,即:
| $ \begin{align} \varphi_{\rm b} =\arctan \frac{x}{l_{{\rm{lb}}}} \end{align} $ | (20) |
由图 1可知,猎豹奔跑时脊柱关节与腿关节具有特定的相位关系,在后腿触地时脊柱发生最大弯曲,随着腿的摆动,脊柱逐渐伸展,在后腿即将离地时脊柱伸展达到最大;前腿触地时,脊柱关节有类似的运动规律。依据猎豹奔跑时脊柱与腿的运动关系对四足机器人腿—脊柱之间的协调运动进行规划。
图 5所示为机器人一个奔跑周期的运动示意图,腿部触地过程用黑色表示,离地过程用灰色表示,虚线为机器人前后腿髋关节的运动轨迹。将机器人后腿触地过程分为3个状态:状态Ⅰ至状态Ⅱ,脊柱屈曲;状态Ⅱ为中间状态,设定此时胸关节和腰关节之间的夹角为相同的初始夹角
| $ \begin{align} \theta_{{\rm{ \delta b}}} & =-\theta_{{\rm{ \delta m}}} \end{align} $ | (21) |
| $ \begin{align} \theta_{{\rm{ \delta m}}} & =\theta_{{\rm{ \delta f}}} \end{align} $ | (22) |

|
图 5 机器人奔跑中脊柱—腿协调运动示意图 Fig.5 Schematic diagram of spine-leg coordinated motion in robot running |
机器人形成稳定的匀速运动,有:
| $ \begin{align} \varphi_{{\rm{freal}}} =\varphi_{{\rm{ftheory}}} -\theta_{{\rm{ \delta f}}} \end{align} $ | (23) |
式中
依据以上约束,将脊柱关节运动与腿部运动耦合,实现脊柱—腿协调运动规划:
| $ \begin{align} \begin{cases} {l_{{\rm{lb}}} =l_{{\rm{lb}}} (t)} \\ {\varphi_{\rm b} =\varphi_{\rm b} (t)} \\ {\theta_{\rm \delta b} =-\theta_{\rm \delta m} (t)} \\ {\theta_{\rm \delta m} =\theta_{\rm \delta m} (t)} \\ {\theta_{\rm \delta f} =\theta_{\rm \delta m} (t)} \\ {\varphi_{\rm f} =\varphi_{{\rm{ftheory}}} (t)-\theta_{\rm \delta f} (t)} \end{cases} \end{align} $ | (24) |
式中,
| $ \begin{align} \dot{\theta}_{\min} & \leqslant \dot{\theta}_{0} \leqslant \dot{\theta}_{\max} \end{align} $ | (25) |
| $ \begin{align} \dot{\theta}_{\min} & =\frac{\theta_{\rm e} -\theta_{\rm s}} {T/2}, \quad \dot{\theta}_{\max} =\frac{2(\theta_{\rm e} -\theta_{\rm s})}{T/2} \end{align} $ | (26) |
式中,
为了充分发挥脊柱运动对腿部运动的增强作用,希望脊柱关节的运动范围和运动速度尽可能大。但是,脊柱关节速度的提高必然导致驱动力矩增大,因此,需要根据实际驱动源性能约束,对脊柱关节传动机构的尺寸和运动轨迹控制参数进行综合考虑,开展多目标优化设计。
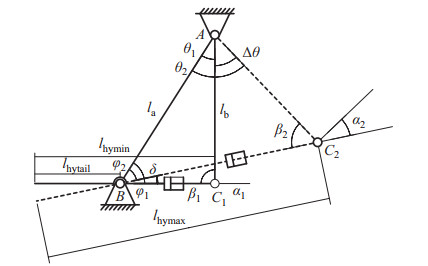
5.1 传动机构的优化目标与约束条件仿猎豹四足机器人脊柱关节采用液压缸驱动的四杆机构,图 6为驱动机构简图,
|
图 6 脊柱关节传动机构示意图 Fig.6 Schematic diagram of the spine joint transmission mechanism |
以脊柱关节运动范围为优化目标对机构尺寸进行优化,根据传动机构几何关系有:
| $ \begin{align} \theta_{i} & =\arccos \frac{l_{\rm a}^{2}+l_{\rm b}^{2}-(l_{{\rm{hy}}j} -l_{{\rm{hytail}}})^{2}}{2l_{\rm a} l_{\rm b}} \end{align} $ | (27) |
| $ \begin{align} \varphi_{i} & =\arcsin \frac{l_{\rm b} \sin \theta_{i}} {l_{{{\rm{hy}}} j} -l_{{\rm{hytail}}}} \end{align} $ | (28) |
| $ \begin{align} \beta_{i} & =\arcsin \frac{l_{\rm a} \sin \theta_{i}} {l_{{\rm{hy}}j} -l_{{\rm{hytail}}}} \end{align} $ | (29) |
| $ \begin{align} \alpha_{i} & =| {\beta_{i} -{\pi } /2} | \end{align} $ | (30) |
式(27)~(30) 中,
取设计变量为
| $ \begin{align} {\mathit{\boldsymbol{ X }}}_{1} =[{l_{\rm a}, l_{\rm b}, l_{{\rm{hytail}}}}]^{\rm T} \end{align} $ | (31) |
以脊柱关节可调节范围最大为优化目标:
| $ \begin{align} \min f({\mathit{\boldsymbol{ X }}}_{1})=-\Delta \theta \end{align} $ | (32) |
根据几何条件确定约束有:
| $ \begin{align} \begin{cases} 0<l_{{{\rm{hy}}}\max} -l_{{{\rm{hy}}}\min} <\max \Delta l_{{\rm{hy}}} \\ l_{{{\rm{hytail}}}\min} <l_{{\rm{hytail}}} <l_{{{\rm{hytail}}}\max} \\ 0<| {l_{\rm a} -l_{\rm b}} |<l_{{{\rm{hy}}}\min} \\ l_{{{\rm{hy}}}\max} <l_{\rm a} +l_{\rm b} \end{cases} \end{align} $ | (33) |
根据力学条件确定约束有:
| $ \begin{align} \begin{cases} \alpha_{\min} \leqslant \alpha \leqslant \alpha_{\max} \\ \tau_{\max} \leqslant F_{{{\rm{hy}}}\max} l_{\rm b} \cos \alpha_{\tau_{\max}} \end{cases} \end{align} $ | (34) |
式中,
关节轨迹的不同直接影响关节驱动力矩的大小,因此需要对关节轨迹控制参数进行优化。针对脊柱关节以及腿部髋关节的运动轨迹,取最大关节速度为设计变量:
| $ \begin{align} {\mathit{\boldsymbol{ X }}}_{2} =[{\dot{\theta}_{{\rm{spine}}}, \dot{\theta}_{{\rm{fleg}}}} ]^{\rm T} \end{align} $ | (35) |
式中
以所需最大关节驱动力矩为优化目标:
| $ \begin{align} \min f({\mathit{\boldsymbol{ X }}}_{2})=\tau_{\max} \end{align} $ | (36) |
根据前文的脊柱关节抛物线运动轨迹,确定约束条件为
| $ \begin{align} \dot{\theta}_{i\min} \leqslant \dot{\theta}_{i} \leqslant \dot{\theta}_{i\max}, \quad i={\rm{spine, fleg}} \end{align} $ | (37) |
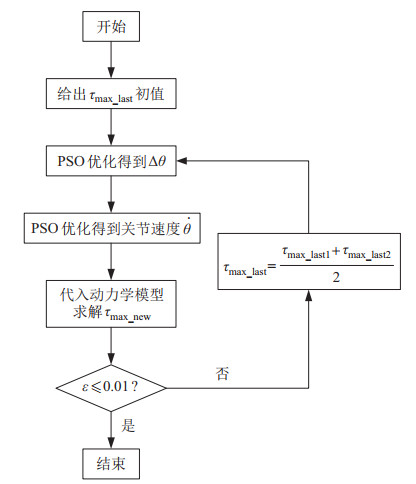
四足机器人的脊柱关节驱动机构的尺寸与其运动轨迹控制参数存在耦合关系,二者均受原动件驱动能力的制约,且2组设计变量相关的优化目标具有互斥关系,因此无法分别优化,本文采用嵌套PSO算法对驱动机构尺寸与运动轨迹进行联合优化,步骤如下:
(1) 首先给出一个初始的最大关节驱动力矩
(2) 将
(3) 将得到的关节轨迹代入动力学模型求出最大关节力矩
由于
|
图 7 传动机构联合优化流程图 Fig.7 Flow chart of the joint optimization of transmission mechanism |
|
|
表 4 脊柱关节驱动机构的尺寸与控制参数优化结果 Tab. 4 Optimization results of the size and control parameters of spine joint actuation mechanism |
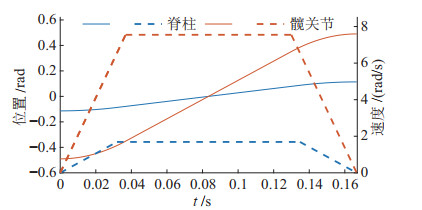
图 8为脊柱关节和腿部运动轨迹,脊柱关节运动范围为0.23 rad,最大速度为1.7 rad/s,腿部髋关节运动范围为0.98 rad,最大速度为7.55 rad/s。
|
图 8 关节轨迹优化结果(图中实线为关节位置曲线,虚线为关节速度曲线) Fig.8 Joint trajectory optimization results (the solid line is the joint position curve, and the dashed line is the joint velocity curve) |
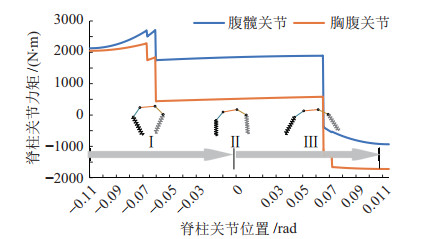
将图 8中脊柱和腿的运动代入四足机器人动力学方程,在运动范围内,求得脊柱关节力矩随脊柱关节角的变化曲线,如图 9所示。与图 5中的3个阶段对应,在状态Ⅰ,脊柱从
|
图 9 奔跑运动中脊柱关节驱动力矩 Fig.9 Spinal joint torque in running |
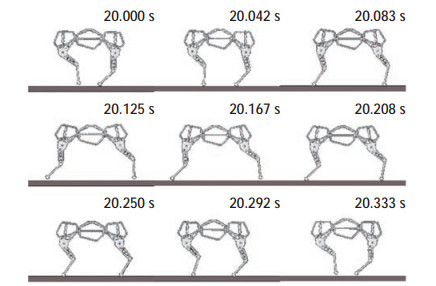
在ADAMS软件中建立仿猎豹四足机器人的虚拟样机模型,分别进行有脊柱跳跃步态奔跑运动及无脊柱跳跃步态奔跑运动仿真,对比分析脊柱对四足机器人运动的影响。
仿真得到一个运动周期的视频截图,见图 10。结果表明:脊柱关节和腿关节的协调控制可以使四足机器人实现稳定的跳跃步态奔跑,其运动模式类似猎豹,胸关节、腰关节角呈周期性变化,躯干与步态对应屈曲伸展,机器人出现四腿离地的腾空相状态。
|
图 10 四足机器人奔跑运动过程 Fig.10 Running process of the quadruped robot |
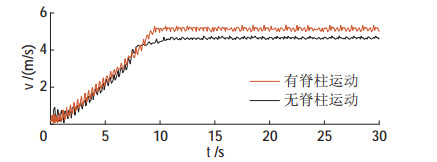
对机器人奔跑时的质心速度及跨步长进行分析,如图 11、图 12所示。机器人从静止开始加速,在15 s时实现稳定运动,有脊柱关节时机器人平均步幅为1.49 m,约等于2.48倍腿长,质心运动速度达到5.15 m/s;无脊柱关节时机器人平均步幅为1.37 m,约等于2.28倍腿长,运动速度为4.68 m/s。对于本文规划的跳跃步态,脊柱运动使机器人步幅增加了8.8%,速度提高了10%,说明脊柱关节与腿部的协调运动可以有效地增大步幅,进而提高机器人的奔跑速度。
|
图 11 机器人奔跑时的质心速度 Fig.11 The speed of the center of mass of the robot in running |
|
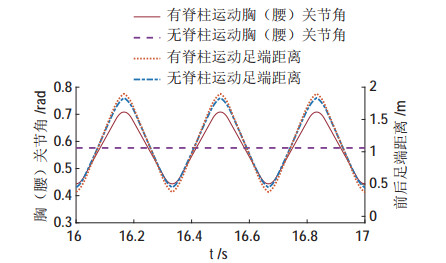
图 12 有、无脊柱条件下运动时脊柱关节角与足端距离对比 Fig.12 Spinal joint angle and foot distance when moving with or without a spine |
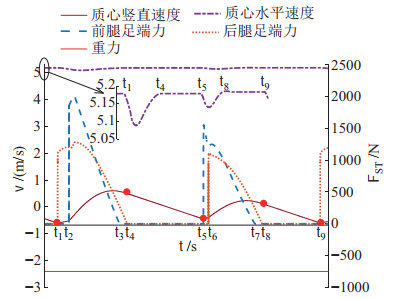
对质心速度及足底地面接触反作用力及脊柱关节力矩进行分析,见图 13,
| $ \begin{align} &\int_{t_{1}}^{t_{4}} F_{{\rm{STH}}} {\rm d}t+\int_{t_{2}}^{t_{3}} F_{\rm{STF}} {\rm d}t+\int_{t_{5}}^{t_{7}} F_{\rm{STF}} {\rm d}t+\int_{t_{6}}^{t_{8}} F_{\rm{STH}} {\rm d}t \\ =& mg(t_{9} -t_{1}) \end{align} $ | (38) |
|
图 13 机器人运动与足端力变化曲线 Fig.13 The robot motion and plantar force curve |
满足式(15) 的四足机器人所受合力冲量为0的条件,因此,机器人可以实现周期性的等速奔跑。
对图 13中腾空相的运动状态进行分析,腾空相的总时长占整个运动周期的47%,腾空相中机器人质心水平速度稳定在5.18 m/s,明显高于其触地相的质心速度,说明腾空相对于维持机器人奔跑速度具有重要作用。
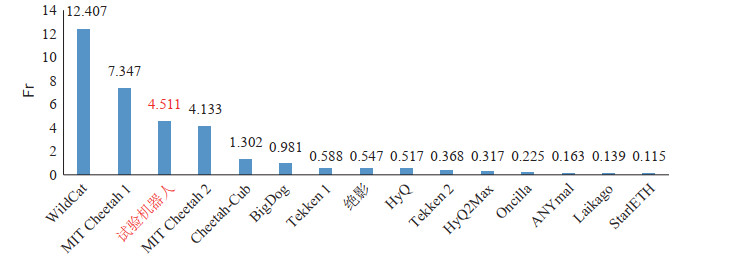
利用式(39) 中定义的弗劳德数(Froude number)[29] 对机器人运动速度进行归一化比较,如图 14所示。
| $ \begin{align} Fr=\frac{\bar{v}^{2}}{gh} \end{align} $ | (39) |
|
图 14 各机器人 |
式中
可以看到,本文的仿猎豹四足机器人(图中实验机器人)的弗劳德数低于WildCat和MIT Cheetah1机器人,高于其他机器人。实验机器人与WildCat和MIT Cheetah1机器人均具有柔性脊柱或主动驱动躯干,而其他机器人为刚性躯干,说明脊柱运动对于提高四足机器人运动速度具有重要作用。
7 结论(Conclusion)本文提出了一种具有2自由度铰接式躯干的仿猎豹四足奔跑机器人,建立了四足机器人跳跃步态动力学模型,对脊柱与腿的协调运动进行了轨迹规划。利用改进的PSO迭代算法解决了目标互斥的脊柱关节驱动机构尺寸和关节轨迹控制参数的嵌套优化问题。对四足机器人跳跃奔跑运动进行动力学仿真,结果表明机器人可以实现稳定的奔跑运动,脊柱运动使腿部运动步幅增大8.8%,使机器人运动速度提高10%。机器人运动过程中出现明显腾空相,腾空相时长占整个运动周期的47%,揭示了腾空相对高速运动的重要作用。具有脊柱关节的四足机器人的形态及运动方式更接近动物本源,具有更大的运动潜力,本文的研究结果对于探索如何将仿生学机理应用于机器人,促进四足机器人技术的发展具有理论意义和应用价值。
| [1] |
Hildebrand M. Motions of the running cheetah and horse[J]. Journal of Mammalogy, 1959, 40(4): 481-495. DOI:10.2307/1376265 |
| [2] |
Hildebrand M. Further studies on locomotion of the cheetah[J]. Journal of Mammalogy, 1961, 42(1): 84-91. DOI:10.2307/1377246 |
| [3] |
Gambaryan P P. How mammals run: Anatomical adaptations[J]. BioScience, 1975, 25(8): 520. |
| [4] |
Schilling N, Hackert R. Sagittal spine movements of small therian mammals during asymmetrical gaits[J]. Journal of Experimental Biology, 2006, 209(19): 3925-3939. DOI:10.1242/jeb.02400 |
| [5] |
Alexander R M, Dimery N J, Ker R F. Elastic structures in the back and their role in galloping in some mammals[J]. Journal of Zoology, 1985, 207(4): 467-482. DOI:10.1111/j.1469-7998.1985.tb04944.x |
| [6] |
Gray J. How animals move[M]. Cambridge, UK: Cambridge University Press, 1953.
|
| [7] |
Semini C, Tsagarakis N G, Guglielmino E, et al. Design of HyQ - A hydraulically and electrically actuated quadruped robot[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2011, 225(I6): 831-849. |
| [8] |
Semini C, Barasuol V, Goldsmith J, et al. Design of the hydraulically actuated, torque-controlled quadruped robot HyQ2Max[J]. IEEE/ASME Transactions on Mechatronics, 2017, 22(2): 635-646. DOI:10.1109/TMECH.2016.2616284 |
| [9] |
Hutter M, Gehring C, Jud D, et al. ANYmal - A highly mobile and dynamic quadrupedal robot[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2016: 38-44.
|
| [10] |
Park H W, Park S, Kim S. Variable-speed quadrupedal bounding using impulse planning: Untethered high-speed 3D running of MIT Cheetah 2[C]//IEEE International Conference on Robotics and Automation. Piscataway, USA: IEEE, 2015: 5163-5170.
|
| [11] |
Bledt G, Powell M J, Katz B G, et al. MIT Cheetah 3: Design and control of a robust, dynamic quadruped robot[C]//IEEE/RSJ International Conference of Intelligent Robots and Systems. Piscataway, USA: IEEE, 2018: 2245-2252.
|
| [12] |
Katz B G. A low cost modular actuator for dynamic robots[D]. Boston, USA: MIT, 2018.
|
| [13] |
刘京运. 从Big Dog到Spot Mini: 波士顿动力四足机器人进化史[J]. 机器人产业, 2018(2): 109-116. Liu J Y. From Big Dog to Spot Mini: Evolution history of Boston Dynamics quadruped robot[J]. Robot Industry, 2018(2): 109-116. |
| [14] |
荣学文. SCalf液压驱动四足机器人的机构设计与运动分析[D]. 济南: 山东大学, 2013. Rong X W. Mechanism design and kinematics analysis of a hydraulically actuated quadruped robot SCalf[D]. Jinan: Shandong University, 2013. |
| [15] |
柴汇, 孟健, 荣学文, 等. 高性能液压驱动四足机器人SCalf的设计与实现[J]. 机器人, 2014, 36(4): 385-391. Chai H, Meng J, Rong X W, et al. Design and implementation of SCalf, an advanced hydraulic quadruped robot[J]. Robot, 2014, 36(4): 385-391. |
| [16] |
Unitree. Laikago[EB/OL]. (2017-10-14)[2021-03-01]. http://www.unitree.cc/cn/e/action/ShowInfo.php?classid=6&id=1.
|
| [17] |
Unitree. Aliengo[EB/OL]. (2021-02-11)[2021-03-01]. http://www.unitree.cc/cn/e/action/ShowInfo.php?classid=6&id=359.
|
| [18] |
朱秋国. "绝影"机器人助力智慧安防[J]. 中国测绘, 2019(3): 31-33. Zhu Q G. "Jue Ying" robot helps intelligent security[J]. China Surveying and Mapping, 2019(3): 31-33. |
| [19] |
Seok S, Wang A, Chuah M Y, et al. Design principles for highly efficient quadrupeds and implementation on the MIT Cheetah robot[C]//IEEE International Conference on Robotics and Automation. Piscataway, USA: IEEE, 2013: 3307-3312.
|
| [20] |
Seok S, Wang A, Chuah M Y, et al. Design principles for energy-efficient legged locomotion and implementation on the MIT cheetah robot[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(3): 1117-1129. DOI:10.1109/TMECH.2014.2339013 |
| [21] |
Zhao Q, Ellenberger B, Sumioka H, et al. The effect of spine actuation and stiffness on a pneumatically-driven quadruped robot for cheetah-like locomotion[C]//IEEE International Conference on Robotics and Biomimetics. Piscataway, USA: IEEE, 2013: 1807-1812.
|
| [22] |
吴海波. 具有可变刚度的四足机器人仿生脊柱设计与应用研究[D]. 北京: 北京交通大学, 2016. Wu H B. Design of a bionic variable stiffness spine and its application to quadruped robot[D]. Beijing: Beijing Jiaotong University, 2016. |
| [23] |
Wang C L, Wang S G. Bionic control of cheetah bounding with a segmented spine[J]. Applied Bionics and Biomechanics, 2016. DOI:10.1155/2016/5031586 |
| [24] |
聂华. 具柔性脊柱的四足机器人结构优化与控制[D]. 武汉: 华中科技大学, 2016. Nie H. Research on structure optimization and control of quadruped robot with flexible spine[D]. Wuhan: Huazhong University of Science and Technology, 2016. |
| [25] |
谭小康. 具有主动脊柱的四足机器人结构设计与仿生控制研究[D]. 北京: 北京交通大学, 2018. Tan X K. Structural design and bionic control of a quadruped robot with actuated spine[D]. Beijing: Beijing Jiaotong University, 2018. |
| [26] |
Raibert M H, Brown H B, Chepponis M Jr. Experiments in balance with a 3D one-legged hopping machine[J]. International Journal of Robotics Research, 1984, 3(2): 75-92. DOI:10.1177/027836498400300207 |
| [27] |
Raibert M H. Trotting, pacing and bounding by a quadruped robot[J]. Journal of Biomechanics, 1990, 23(1): 79-81, 83-98. |
| [28] |
Raibert M. H. Legged robots that balance[M]. Boston, USA: MIT Press, 1986.
|
| [29] |
Eckert P. Towards agility: Definition, benchmark and design considerations for small, quadrupedal robots[D]. Lausanne, Switzerland: Swiss Federal Institute of Technology in Lausanne, 2018.
|
 2022, Vol. 44
2022, Vol. 44


