2. 中国科学院沈阳自动化研究所机器人学国家重点实验室, 辽宁 沈阳 110016;
3. 中国科学院机器人与智能制造创新研究院, 辽宁 沈阳 110169;
4. 辽宁省水下机器人重点实验室, 辽宁 沈阳 110016
2. State Key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences, Shengyang 110016, China;
3. Institutes for Robotics and Intelligent Manufacturing, Chinese Academy of Sciences, Shenyang 110169, China;
4. Key Laboratory of Marine Robotics, Liaoning Province, Shenyang 110016, China
AUV一直是智能装备领域的研究热点,已经在海洋科学研究、海洋资源调查和海洋安全保障等方面得到广泛的应用[1-2]。近年来,研究人员将AUV作为观测器用于对鲸鱼、海豚等海洋生物生活习性的调查,这些海洋生物的运动速度较快,要求AUV尽快与目标汇合并保持跟踪[3]。在此,本文将这些海洋生物称作“运动目标”。
AUV在对水下运动目标进行追踪时,通常依靠自身携带的声学测量系统,基于被动接收到的运动目标的方位和距离信息,对运动目标的航行参数进行在线估算,这种方法一般称为方位—距离平差法[4]。
在方位—距离平差法的基本框架下,采用经典最小二乘算法对目标运动参数进行分析时,基于全部采样数据完成一次迭代处理。随着时间的推移,累积采样的数据越来越多,采用这种一次完成迭代过程的算法需要存储所有的数据,严重耗费微处理器的内存资源,不能满足目标运动参数实时解算的要求[5]。
为了解决该问题,本文提出了一种迭代优化算法,该算法利用渐消记忆递推最小二乘(FMRLS)算法对运动目标的航行参数进行解算,AUV每取得一个目标方位和距离数据,就根据新数据对目标运动参数估计量进行修正,从而得到改善后的新的目标运动参数估计量[6-8];同时为了解决FMRLS算法有时带来的数值不稳定问题,将平方根算法与FMRLS算法相结合。这种新的迭代优化算法既能保证数据的快速收敛,又能确保数值的稳定性。
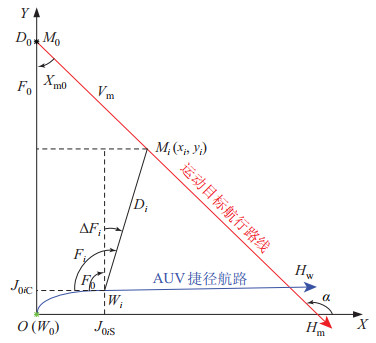
2 方位—距离平差法的计算模型(Calculation model of the bearing-distance adjustment method)如图 1所示,在运动目标等速直航的假定条件下,其航向线为一条直线,该直线方程的表示可分2种情况进行讨论。
|
图 1 AUV与运动目标之间的几何关系 Fig.1 Geometric relationship between the AUV and the moving target |
(1) 一般情况,即直线的斜率存在。此时,可用斜截式直线方程
(2) 特殊情况,即直线的斜率不存在。此时,可用一般的直线方程
先考虑一般情况,以AUV初始位置点
| $ \begin{align} \begin{cases} {x_{i} =J_{{0i{\rm S}}} +D_{i} \sin \Delta F_{i}} \\ {y_{i} =J_{{0i{\rm C}}} +D_{i} \cos \Delta F_{i}} \end{cases} \end{align} $ | (1) |
其中
声学系统测量及采样输入的运动目标方位和距离信息必然存在误差;同样,AUV根据其导航设备推算出的横向位移和纵向位移也存在一定的误差。直线的斜截式方程
| $ \begin{align} J_{0i{\rm C}} +D_{i} \cos \Delta F_{i} -K(J_{ 0i\rm S} +D_{i} \sin \Delta F_{i})-D_{0} =\varepsilon_{i} \end{align} $ | (2) |
根据递推最小二乘算法的基本原理,以及AUV采集到的实时运动目标方位和距离信息,对方程式(2) 进行系统辨识,得到直线的斜率
在解算得到
| $ \begin{align} \begin{cases} \alpha ={\rm{\pi }} -\arctan K\; (K>0)\\ \qquad {\rm{或 }}\;\alpha ={\rm{\pi }} +\arctan K\; (K<0) \\ X_{\rm m0} =\alpha -90^{{\circ}} \\ H_{\rm m} =F_{0} +180^{{\circ}}-X_{\rm m0} \\ V_{\rm m} =\dfrac{(D_{0} -J_{0i\rm C})\sin \Delta F_{i} +J_{0i\rm S} \cos \Delta F_{i}} {t_{0i} \sin (X_{\rm m0} +\Delta F_{i})} \end{cases} \end{align} $ | (3) |
对于非特殊情况(
令
| $ \begin{align} y(i)={\mathit{\boldsymbol{\varphi}}}_{i}^{\rm T} {\mathit{\boldsymbol{\theta}}} +\varepsilon_{i} \end{align} $ | (4) |
依照FMRLS算法对方程式(4) 进行辨识,实时递推公式可表示成
| $ \begin{align} \hat{\mathit{\boldsymbol{\theta}}}_{N+1}=\;&\hat{\mathit{\boldsymbol{\theta}}}_{N} +\frac{{\mathit{\boldsymbol{P}}}_{N} \mathit{\boldsymbol{\varphi}}_{N+1}} {\mathit{\boldsymbol{\varphi}}_{N+{1}}^{\rm T} {\mathit{\boldsymbol{P}}}_{N} {\mathit{\boldsymbol{\varphi}}}_{N+1} +\rho}\times\\ &[y(N+1)-{\mathit{\boldsymbol{\varphi}}}_{N+1}^{\rm T} \hat{\mathit{\boldsymbol{\theta}}}_{N}] \end{align} $ | (5) |
| $ \begin{align} {\mathit{\boldsymbol{P}}}_{N+1} =\;&{\mathit{\boldsymbol{P}}}_{N} -\frac{{\mathit{\boldsymbol{P}}}_{N} {\mathit{\boldsymbol{\varphi}}}_{N+1} {\mathit{\boldsymbol{\varphi}}}_{N+1}^{\rm T} {\mathit{\boldsymbol{P}}}_{N}} {{\mathit{\boldsymbol{\varphi}}}_{N+1}^{\rm T} {\mathit{\boldsymbol{P}}}_{N} {\mathit{\boldsymbol{\varphi}}}_{N+1} +\rho} \end{align} $ | (6) |
其中常数
| $ \begin{align} y_{k} &=J_{0k\rm C} +D_{k} \cos \Delta F_{k} \end{align} $ | (7) |
| $ \begin{align} {\mathit{\boldsymbol{X}}}_{k} &=[J_{0k\rm S} +D_{k} \sin \Delta F_{k}, 1]^{\rm T} \end{align} $ | (8) |
| $ \begin{align} {\mathit{\boldsymbol{K}}}(k+1)&={\mathit{\boldsymbol{P}}}(k){\mathit{\boldsymbol{\varphi}}}_{k+1} /\big(\rho +{\mathit{\boldsymbol{\varphi}}}_{k+1}^{\rm T} {\mathit{\boldsymbol{P}}}(k){\mathit{\boldsymbol{\varphi}}}_{k+1}\big) \end{align} $ | (9) |
| $ \begin{align} {\mathit{\boldsymbol{\theta}}} (k+1)&={\mathit{\boldsymbol{\theta}}} (k)+{\mathit{\boldsymbol{K}}}(k+1)\big(y_{k+1} -{\mathit{\boldsymbol{\varphi}}}_{k+1}^{\rm T} {\mathit{\boldsymbol{\theta}}} (k)\big) \end{align} $ | (10) |
| $ \begin{align} {\mathit{\boldsymbol{P}}}(k+1)&=\big({\mathit{\boldsymbol{P}}}(k)-{\mathit{\boldsymbol{K}}}(k+1){\mathit{\boldsymbol{\varphi}}}_{k+1}^{\rm T} {\mathit{\boldsymbol{P}}}(k)\big)/\rho \end{align} $ | (11) |
矩阵
(1) 给定初始值
(2) 进行第
(3) 计算预测误差
(4) 依据式(9) 计算增益
(5) 根据方程式(10) 修正估计值
(6) 按照方程式(11) 计算协方差
(7)
在对目标运动参数进行估算时,递推参数估计是由字长有限的微处理器来实现的,需要进行上万次的迭代运算,而在迭代运算过程中,并不是每种递推算法都能保证数值的稳定性。同理,在本文的FMRLS算法中,也存在数值不稳定的问题,下面来给予证明。
证明 在本文所考虑的有2个参数的运动目标航行参数估计的解算模型中,依据方程式(10) 可以得到以下参数估计误差方程:
| $ \begin{align} \Delta {\mathit{\boldsymbol{\theta}}} (k\!+\!1) \! &={\mathit{\boldsymbol{\theta}}} -{\mathit{\boldsymbol{\theta}}}(k+1) \\ &={\mathit{\boldsymbol{\theta}}} -{\mathit{\boldsymbol{\theta}}} (k)-{\mathit{\boldsymbol{K}}}(k+1)\big(y_{k+1} -{\mathit{\boldsymbol{\varphi}}}_{k+1}^{\rm T} {\mathit{\boldsymbol{\theta}}} (k)\big) \\ &=\Delta {\mathit{\boldsymbol{\theta}}} (k)-{\mathit{\boldsymbol{K}}}(k\!+\!1)y_{k+1} +{\mathit{\boldsymbol{K}}}(k\!+\!1){\mathit{\boldsymbol{\varphi}}}_{k+1}^{\rm T} {\mathit{\boldsymbol{\theta}}} (k) \\ &=\big({\mathit{\boldsymbol{I}}}-{\mathit{\boldsymbol{K}}}(k+1){\mathit{\boldsymbol{\varphi}}}_{k+1}^{\rm T} \big)\Delta {\mathit{\boldsymbol{\theta}}} (k)-{\mathit{\boldsymbol{K}}}(k+1)\varepsilon_{k+1} \end{align} $ | (12) |
这是一个随机误差方程,其中
由增益的递推公式,可得:
| $ \begin{align} {\mathit{\boldsymbol{K}}}(k+1){\mathit{\boldsymbol{\varphi}}}_{k+1}^{\rm T} =\frac{{\mathit{\boldsymbol{P}}}(k){\mathit{\boldsymbol{\varphi}}}_{k+1} {\mathit{\boldsymbol{\varphi}}}_{k+1}^{\rm T}} {\rho +{\mathit{\boldsymbol{\varphi}}}_{k+1}^{\rm T} {\mathit{\boldsymbol{P}}}(k){\mathit{\boldsymbol{\varphi}}}_{_{k+1}}} \end{align} $ | (13) |
而方阵
| $ \begin{align} \begin{cases} {{\mathit{\boldsymbol{P}}}(k)\rm{\; 的特征根都小于}\; 0} \\ {|{\mathit{\boldsymbol{\varphi}}}_{k+1}^{\rm T} {\mathit{\boldsymbol{P}}}(k){\mathit{\boldsymbol{\varphi}}}_{k+1} |<\rho} \end{cases} \end{align} $ | (14) |
这就是说,一旦方阵
为了避免上述问题的产生,防止在递推过程中方阵
在方程式(4) 的基础上,定义以下公式:
| $ \begin{align} &{{\mathit{\boldsymbol{f}}}}_{k+1} ={{{\mathit{\boldsymbol{S}}}}^{\rm T}}(k+1){\mathit{\boldsymbol{\varphi}}}_{k+1} \end{align} $ | (15) |
| $ \begin{align} &\beta_{k+1} =\rho +{{\mathit{\boldsymbol{f}}}}_{k+1}^{\rm T} {{\mathit{\boldsymbol{f}}}}_{k+1} \end{align} $ | (16) |
| $ \begin{align} &\alpha_{k+1} =1/{(\beta_{k+1} +\sqrt{\rho \beta_{k+1}})} \end{align} $ | (17) |
| $ \begin{align} &{\mathit{\boldsymbol{Q}}}(k+1)={\mathit{\boldsymbol{S}}}(k+1){{\mathit{\boldsymbol{f}}}}_{k+1} /\beta_{k+1} \end{align} $ | (18) |
| $ \begin{align} &{\mathit{\boldsymbol{\theta}}} (k+1)={\mathit{\boldsymbol{\theta}}} (k)+{\mathit{\boldsymbol{Q}}}(k+1)\big(y_{k+1} -{\mathit{\boldsymbol{\varphi}}}_{k+1}^{\rm T} {\mathit{\boldsymbol{\theta}}} (k)\big) \end{align} $ | (19) |
| $ \begin{align} &{\mathit{\boldsymbol{S}}}(k+1)=1/{\sqrt{\rho}} \big({{\mathit{\boldsymbol{I}}}-\alpha_{k+1} \beta_{k+1} {\mathit{\boldsymbol{Q}}}(k+1){\mathit{\boldsymbol{\varphi}}}_{k+1}^{\rm T}}\big){\mathit{\boldsymbol{S}}}(k) \end{align} $ | (20) |
其中
(1) 给定初始值
(2) 进行第
(3) 计算预测误差
(4) 依据式(18) 计算增益
(5) 根据方程式(19) 修正估计值
(6) 按照方程式(20) 计算协方差
(7)
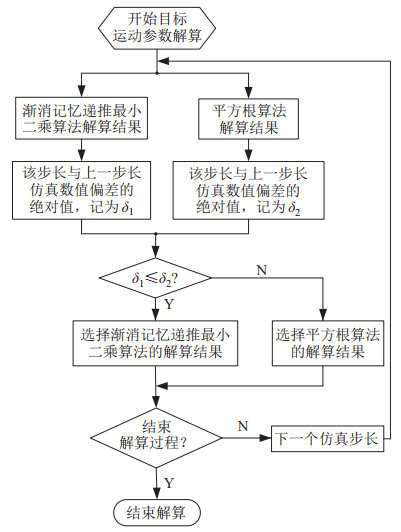
在目标运动参数实时解算过程中,并行利用FMRLS算法和平方根算法,并在2种算法内部比较相邻2个仿真步长解算出的数值偏差,依据偏差来选择最优的目标运动参数。该算法的计算流程如图 2所示。
|
图 2 迭代优化算法的计算流程 Fig.2 Calculation process of the iterative optimization algorithm |
在AUV利用方位—距离平差法对目标运动参数进行解算的过程中,根据目标航行直线的斜率及其速度符号可以确定目标的运动方向,但目标运动速度的解算是最难收敛的,也最易受其他变量的扰动影响。由式(3) 可以看出:目标运动速度跟多个变量有关,既跟初始距离、初始舷角有关,又跟目标方位的变化量、AUV的横向和纵向位移有关,任何一个变量发生变化,都会使目标速度信息发生改变。因此,对各个变量的变化范围有一个明确的定义是正确进行目标运动参数解算的前提。
根据运动目标与AUV之间的相对运动状态,可将目标分为以下4种情况:目标处于AUV坐标系的第一、第二、第三以及第四象限,具体情形如图 3所示。

|
图 3 种情况下移动目标与AUV之间的相对运动状态图 Fig.3 Relative motion states between the moving target and the AUV in the 4 situations |
由图 3可以看出,运动目标方位变化量的正切函数可表示为
| $ \begin{align} {\rm{tan}}\Delta F_{i} =\frac{t_{0i} V_{\rm m} \sin X_{\rm m0} -J_{0i\rm S}} {D_{0} -t_{0i} V_{\rm m} \cos X_{\rm m0} -J_{0i\rm C}} =\frac{\sin \Delta F_{i}} {\cos \Delta F_{i}} \end{align} $ | (21) |
由式(16) 可推导出此时的目标运动速度为
| $ \begin{align} V_{\rm m} =\frac{(D_{0} -J_{0i\rm C})\sin \Delta F_{i} +J_{0i\rm S} \cos \Delta F_{i}} {t_{0i} \sin (X_{\rm m0} +\Delta F_{i})} \end{align} $ | (22) |
依据方程式(22) 中各个变量的取值范围,可以推导出以上4种情况下目标运动速度的符号及其量值,具体如表 1所示。
|
|
表 1 4种情况下变量的取值范围及目标速度的符号 Tab. 1 Value ranges of the variables and signs of the target speed in the 4 situations |
因FMRLS算法以及平方根算法中均含有遗忘因子
在此,给定一种具体情形:目标与AUV之间的初始距离为1200 m、目标航向角为
设定

|
图 4 AUV与运动目标之间的相对运动状态 Fig.4 Relative motion state between the AUV and the moving target |
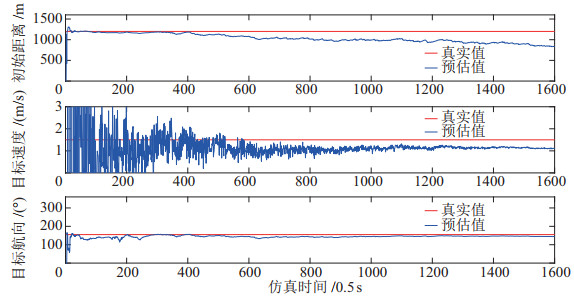
|
图 5 遗忘因子为0.99时的目标运动参数解算结果 Fig.5 Calculation result of the target motion parameters when the forgetting factor is 0.99 |

|
图 6 遗忘因子分别为0.999、0.9999和1.0时的目标运动参数解算结果 Fig.6 Calculation results of the target motion parameters when the forgetting factor is 0.999, 0.9999 and 1.0 respectively |
从仿真结果可以看出,在800 s的仿真时间内,遗忘因子小于或等于0.99时,方位—距离平差法解算出来的目标运动参数都是发散的,遗忘因子数值越接近1.0;目标运动参数解算收敛的时间越短,解算的效果也越好。在此,我们选择的遗忘因子数值为0.999(解算精度已满足实际需求)。
6.2 各种场景下的目标航行参数分析 6.2.1 基本假设为了充分证明迭代优化算法在运动目标航行参数解算中的有效性,设计了6种典型场景,具体见表 2。场景1~场景4为AUV匀速直线航行,运动目标分别处于AUV坐标系的第一、第二、第三和第四象限;场景5为AUV悬停,运动目标从AUV坐标系的第一象限向第四象限穿越,场景6为AUV悬停,运动目标从AUV坐标系的第二象限向第三象限穿越。
|
|
表 2 6种场景下的参数设置 Tab. 2 Parameters setting in the 6 situations |
在仿真实验中,设定运动目标的方位测量误差为
(1) 当AUV匀速直航时
场景1~场景4运动目标航行参数的解算结果如图 7所示,解算的参数主要包括运动目标的初始距离、运动速度和航向角。

|
图 7 AUV匀速直航时的目标运动参数解算结果 Fig.7 Calculation results of target motion parameters when AUV sails in a straight line at a constant speed |
从图 7可看出,在给定的运动目标距离和方位测量误差下,迭代优化算法能快速解算出运动目标的初始距离、航向角及运动方向,数值收敛时间约3 min,目标速度信息也能够在5 min左右收敛,并且目标的初始距离越近,数值收敛的速度越快。
(2) 当AUV悬停时
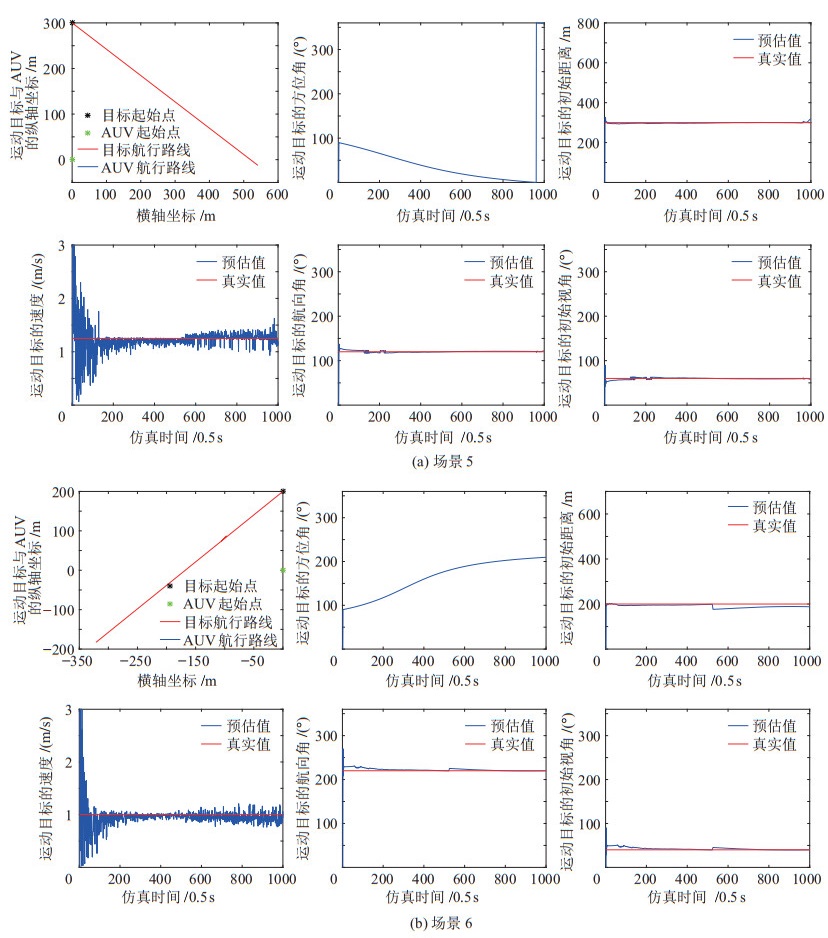
场景5和场景6这2种情况下,运动目标的航行参数解算结果如图 8所示。解算的参数包括运动目标的初始距离、方位角、运动速度、航向角以及初始视角。
|
图 8 AUV悬停时的目标运动参数解算结果 Fig.8 Calculation results of target motion parameters when AUV is hovering |
从仿真结果可以看出,当运动目标与AUV之间的相对运动状态发生象限穿越,甚至当运动目标的相对方位发生360°突变时,迭代优化算法解算出来的目标运动参数还能继续保持收敛。
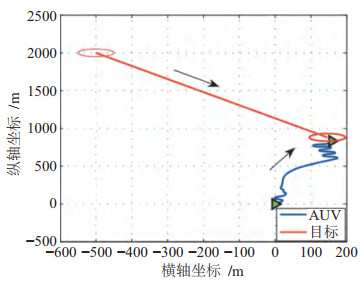
6.3 与纯方位目标跟踪算法的对比分析为了进一步验证迭代优化算法相较于其他算法的优越性,选用场景1,利用纯方位目标跟踪算法[11-12]对目标的航行参数进行解算,解算结果如图 9所示。
|
图 9 AUV纯方位目标跟踪解算结果 Fig.9 Calculation results of bearing-only target tracking |
由图 9可以看出,当采用纯方位目标跟踪算法时,为了确保目标运动参数的解算数据趋于收敛,AUV必须做机动航行,这对于AUV的机动性能提出了更高的要求,对其机载电池容量也是一个不小的挑战。
7 结论(Conclusion)本文依据AUV采样输入的运动目标方位和距离信息,采用方位—距离平差法对目标航行参数进行解算,针对经典最小二乘算法难以满足目标运动参数实时解算要求这一问题,在给出渐消记忆递推最小二乘(FMRLS)算法以及该算法可能带来的数值不稳定性证明的基础上,提出一种将FMRLS算法与平方根算法相结合的迭代优化算法,以保证数据的快速收敛和数值的稳定性。多种场景下的计算机仿真结果证明,该迭代优化算法的鲁棒性好,无需AUV作任何机动航行,甚至可以悬停,适合应用于AUV对水下运动目标进行追踪,为这一工程实际问题提供了一种有效解决办法。
| [1] |
徐会希, 姜成林. 基于USV与AUV异构平台协同海洋探测系统研究综述[J]. 中国科学院大学学报, 2021, 38(2): 145-159. Xu H X, Jiang C L. Heterogeneous oceanographic exploration system based on USV and AUV: A survey of developments and challenges[J]. Journal of University of Chinese Academy of Sciences, 2021, 38(2): 145-159. |
| [2] |
李一平, 李硕, 张艾群. 自主/遥控水下机器人研究现状[J]. 工程研究, 2016, 8(2): 217-222. Li Y P, Li S, Zhang A Q. Research status of autonomous & remotely operated vehicle[J]. Journal of Engineering Studies, 2016, 8(2): 217-222. |
| [3] |
王艳艳, 刘开周, 封锡盛. AUV纯方位目标跟踪轨迹优化方法[J]. 机器人, 2014, 36(2): 179-184. Wang Y Y, Liu K Z, Feng X S. Optimal AUV trajectories for bearings-only tracking[J]. Robot, 2014, 36(2): 179-184. |
| [4] |
董志荣. 主动声呐浮标目标运动分析数学模型[J]. 电光与控制, 2007, 14(1): 5-9. Dong Z R. Mathematical models for target moving analysis through active sonobuoy[J]. Electronics Optics & Control, 2007, 14(1): 5-9. DOI:10.3969/j.issn.1671-637X.2007.01.002 |
| [5] |
Zhang S, Zheng W X. Performance analysis of compressive diffusion normalized LMS algorithm with link noises[C]//IEEE Internatioanl Symposium on Circuits and Systems. Piscataway, USA: IEEE, 2021. DOI: 10.1109/ISCAS51556.2021.9401635.
|
| [6] |
方桂花, 王鹤川, 高旭. 基于动态遗忘因子递推最小二乘法的永磁同步电机参数辨识算法[J]. 计算机应用与软件, 2021, 38(1): 280-283. Fang G H, Wang H C, Gao X. Parameter identification algorithm of permanent magnet synchronous motor based on dynamic forgetting factor recursive least square method[J]. Computer Applications and Software, 2021, 38(1): 280-283. DOI:10.3969/j.issn.1000-386x.2021.01.047 |
| [7] |
钱虹, 江诚, 潘岳凯, 等. 基于自适应遗忘因子RLS算法的稳压器模型在线辨识[J]. 核动力工程, 2019, 40(6): 124-129. Qian H, Jiang C, Pan Y K, et al. Online identification of regulator model based on adaptive forgetting factor RLS algorithm[J]. Nuclear Power Engineering, 2019, 40(6): 124-129. |
| [8] |
冀大雄, 封锡盛, 刘开周, 等. 综合权值递推最小二乘法估计从UUV航行参数[C]//中国仪器仪表与测控技术报告大会论文集. 2008: 310-312. Ji D X, Feng X S, Liu K Z, et. al. Slave-UUV motion analysis using RLS algorithm with synthetical weight[C]//Proceedings of China Instrumentation and Measurement and Control Technology Report Conference. 2008: 310-312. |
| [9] |
韩曾晋. 自适应控制[M]. 北京: 清华大学出版社, 1995. Han Z J. Adaptive control[M]. Beijing: Tsinghua University Press, 1995. |
| [10] |
张树春, 胡广大. 平方根滤波及其在目标跟踪方面的应用[J]. 哈尔滨工业大学学报, 2008, 40(5): 700-704. Zhang S C, Hu G D. Square root filtering and its application in target tracking[J]. Journal of Harbin Institute of Technology, 2008, 40(5): 700-704. DOI:10.3321/j.issn:0367-6234.2008.05.007 |
| [11] |
Alexandri T, Diamant R. A reverse bearings only target motion analysis for autonomous underwater vehicle navigation[J]. IEEE Transactions on Mobile Computing, 2019, 18(3): 494-506. DOI:10.1109/TMC.2018.2840997 |
| [12] |
Clavard J, Pillon D, Pignol A C, et al. Bearings-only target motion analysis of a source in a circular constant speed motion from a non-manueuvering platform[C]//14th International Conference on Information Fusion. Piscataway, USA: IEEE, 2011.
|
 2022, Vol. 44
2022, Vol. 44


