2. 浙江省种植装备技术重点实验室, 浙江 杭州 310018
2. Key Laboratory of Transplanting Equipment and Technology of Zhejiang Province, Hangzhou 310018, China
目前,农业智能化生产(例如果蔬智能采摘)和危险环境的特种检测(例如石油化工厂的泄漏检测)中也需要大量应用机械臂。由于这些机械臂均是安装在移动小车上,且工作在半结构化或非结构化环境中,因此要求机械臂具备低功耗和高安全性特征。传统的工业机械臂虽然精度高、功能齐全,但是较大的重量和转动惯量导致能耗大,大刚度使其安全性较差,这些缺点限制了其在非工业领域的应用。而绳驱动机械臂采用柔性绳索作为传动介质,可以实现远距离传动,这样方便将驱动电机放于基座或腰部,大大减小了机械臂的重量和惯量,从而减小了功耗。而且绳索具有一定的柔顺性,在安全性方面也具有很大的优势。
因此,绳驱动机器人也成为了国内外许多学者们的研究热点并被应用在众多领域,比如外骨骼机器人[1]。Perry等[2]设计了一种具有低惯性、高刚度、零间隙、可反向驱动的绳驱动外骨骼康复机器人。Kirchhoff团队[3-4]研制了一款绳索与弹簧组合驱动的拟肌腱驱动机械臂BioRob,其优点是使机械结构更节能、更安全,可防止操作人员与机器人碰撞造成损伤[5]。陈伟海等[6-8]设计了一种用于外骨骼康复的7自由度绳驱动的串并混联拟人臂机器人。
然而,由于绳驱动机械臂的电机放于基座,后端关节的驱动绳索在穿过前端关节时会发生运动耦合现象,因此有必要设计合适的绳轮机构以实现关节间的运动解耦。美国麻省理工学院Townsend团队[9]经过多年研究,开发了一款利用差速轮原理实现关节运动解耦的绳驱动机械臂WAM,具有良好的交互性和柔顺性,在医疗康复方面得到广泛的应用[10]。Zhao等[11]设计的一种绳驱动医疗手术夹钳,利用行星齿轮的转动特点解决了关节间的运动耦合问题。南京航空航天大学机器人研究团队[12-13]设计了2种模块化解耦结构,可实现多关节间的运动解耦。Kim[14]应用滚动接触关节研制了一种低惯量、高刚度、高速的7自由度拟人机械臂,该机械臂包含一个运动解耦的3自由度并联手腕[15]。Scarcia等[16]等设计了一种绳索通过手腕旋转中心的机构,从而实现手指和手腕的运动解耦。Lee等[17]设计了一款BTDSM机械臂,该机械臂提出了3种不同的解耦结构用以实现不同关节间的运动解耦。Shah等[18]应用运动滑轮思想设计了一种保证固定部件和移动部件之间绳索长度恒定的结构,从而实现各个关节间的运动解耦。
以上结构虽然可以实现关节间的运动解耦或近似解耦,但机械结构和绳索的预紧方式均较为复杂,导致关节笨重,且对零部件的机械加工精度要求高。此外,绳驱动机械臂在运动过程中,绳索的弹性形变对机械臂的运动也会产生一定的影响,使机械臂的关节转角发生偏移。针对上述问题,本文借鉴滑轮运动的思想,提出了一种简单的利用动滑轮实现绳驱动关节运动解耦的方法。在此基础上,进一步分析机械臂因绳索弹性形变而产生的关节转角偏移现象,为机械臂的精确运动控制提供理论基础。
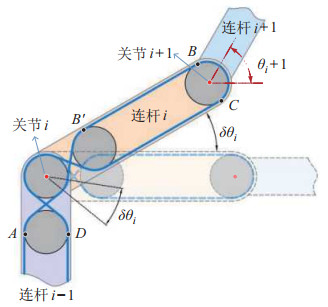
2 绳驱动关节运动解耦方法(Motion decoupling method for cable-driven joints) 2.1 绳驱动关节运动耦合现象图 1显示了绳驱动机械臂的一部分结构,其中包含2个关节、3根连杆。如图 1所示,驱动关节
|
图 1 关节运动耦合现象 Fig.1 Description of the joint motion coupling |
假设连杆
为便于叙述,将绳索未绕在绳轮上的部分称为自由段,如图 1中的
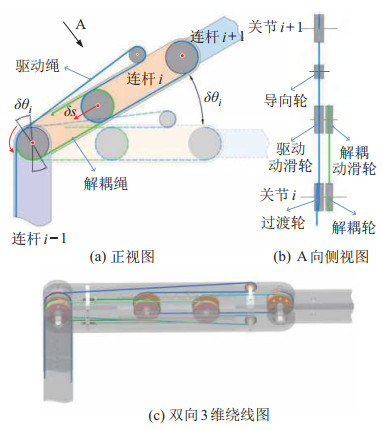
根据该思路,本文设计了一种解耦机构,其绕线方式和解耦原理如图 2所示。图 2(a)(b)中仅描述关节
|
图 2 解耦机构的原理图及绕线方式 Fig.2 Principle of the decoupling mechanism and its winding way |
根据几何关系可知,各个绳轮的位置及半径会影响关节的解耦效果。实现关节运动解耦的充分条件为:
(1) 关节
(2) 所有绕经动滑轮的自由段绳索都必须相互平行。
如图 2所示,仅当关节
提出的解耦机构相对于非解耦机构主要增加了可移动的动滑轮和固定在基座上的解耦轮,其结构相对简单。若要实现跨多关节的运动解耦,则在跨越的所有关节上增加相应的解耦机构即可。而当两关节旋转轴线垂直时,可利用导向轮改变驱动绳的走线方式[9],再应用该解耦机构便可实现垂直关节间的运动解耦。
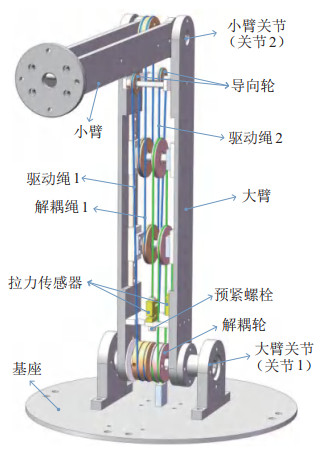
3 2自由度绳驱动机械臂的设计与分析(Design and analysis on the 2-DOF cable-driven manipulator) 3.1 结构设计为验证上述解耦方法的可行性,设计了一个2自由度绳驱动机械臂,其3维模型如图 3所示。由于在2自由度机械臂中,大臂的驱动形式不影响系统的耦合关系,所以为简化模型,大臂关节(关节1)直接用电机驱动。小臂关节(关节2)由2根绳索驱动,分别为驱动绳1和驱动绳2。解耦绳的一端固定在解耦轮上(该解耦轮与基座固连),另一端连接拉力传感器。导向轮的半径是其余轮半径的一半,其余轮的半径均相等。
|
图 3 2自由度绳驱动解耦机械臂模型 Fig.3 Model of the 2-DOF cable-driven decoupling manipulator |
绳驱动机械臂需要在初始状态时预紧绳索。根据该机械臂的力传递特点可知,所有绳索的受力都是相关的,因此只需预紧其中一根绳索,即可实现该关节所有绳索的预紧。针对图 3设计的结构,选择在解耦绳索上加入预紧结构是最简单的预紧方式。在解耦绳自由段的末端连上一个螺栓,通过转动螺栓即可调节绳索的松紧。由于该解耦绳的存在,可以很方便地安装拉力传感器以测量绳索的拉力。相比于其他解耦机构,提出的解耦结构和预紧方式更简单、有效。
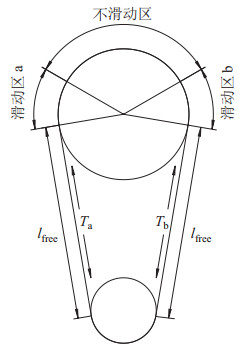
3.2 关节转角偏移分析在绳驱动机械臂的运动过程中,由于绳索的弹性形变会使机械臂关节产生一定的转角偏移和振动,从而影响关节的解耦效果,因此有必要对该转角偏移现象进行分析。由绞盘传动理论可知绳索在自由段的形变为线性弹性形变[19];而包络在绳轮上的绳索因为受到摩擦力的作用,其弹性形变为非线性的。如图 4所示,绕在绳轮上的绳索可以分为3个区域:滑动区a、滑动区b和不滑动区。假设滑动区a为紧边,其拉力大于预紧力(
|
图 4 绳索受力、形变图 Fig.4 Force and deformation of the cable |
令滑动区的形变量为
| $ \begin{equation} {\rm \Delta} l=\frac{ \left({T_{i} -T_{\rm p}} \right)l_{{\rm free}} }{E}, \; \; i={\rm a}, {\rm b} \end{equation} $ | (1) |
滑动区a的形变量为
| $ \begin{equation} {\Delta} s_{{\rm a}} =\frac{r}{E\mu} \left({T_{{\rm a}} -T_{\rm p} -T_{\rm p} \ln \frac{T_{{\rm a}}} {T_{\rm p}}} \right) \end{equation} $ | (2) |
滑动区b的形变量为
| $ \begin{align} {\rm \Delta} s_{{\rm b}} =\frac{r}{E\mu} \left({T_{\rm p} -T_{{\rm b}} +T_{\rm p} \ln \frac{T_{{\rm b}}} {T_{\rm p}}} \right) \end{align} $ | (3) |
其中
由上述理论可根据绳索的拉力计算得到解耦机构中各段绳索的弹性形变量。如图 2所示(为便于解释,图中只显示1对绳索),解耦绳绕在2个绳轮上,共有3个滑动区,驱动绳索绕在4个绳轮上,共有6个滑动区。令导向轮的半径为
| $ \begin{align} {\Delta} l_{{\rm da}} =3{\rm \Delta} s_{{\rm a}} +\frac{T_{{\rm a}} \left({l_{{\rm da}} +\delta s} \right)-T_{\rm p} l_{{\rm da}}} {E} \end{align} $ | (4) |
松边解耦绳的总形变量为
| $ \begin{equation} {\rm \Delta} l_{{\rm db}} =3{\rm \Delta} s_{{\rm b}} +\frac{T_{{\rm b}} \left({l_{{\rm db}} -\delta s} \right)-T_{\rm p} l_{{\rm db}}} {E} \end{equation} $ | (5) |
紧边驱动绳的总形变量为
| $ \begin{equation} \Delta l_{{\rm qa}} =5{\rm \Delta} s_{{\rm a}} +\frac{T_{{\rm a}} \left( {l_{{\rm qa}} -\delta s} \right)-T_{\rm p} l_{{\rm qa}}} {E} \end{equation} $ | (6) |
松边驱动绳的形变量为
| $ \begin{equation} \Delta l_{{\rm qb}} =5{\rm \Delta} s_{{\rm b}} +\frac{T_{{\rm b}} \left( {l_{{\rm qb}} +\delta s} \right)-T_{\rm p} l_{{\rm qb}}} {E} \end{equation} $ | (7) |
根据该解耦结构的传动特点可知,解耦绳索的形变也会导致驱动绳索自由段的长度改变,但是该长度的改变量很小,对绳索自由段形变的影响可忽略不计。所以关节2弧长偏移量为解耦绳和驱动绳的形变量之和。由此,分别得到关节2弧长紧边和松边的总形变量
| $ \begin{align} {\Delta} L_{{\rm a}}& =\Delta l_{{\rm da}} +{\rm \Delta} l_{{\rm qa}} =8{\rm \Delta} s_{{\rm a}} +\frac{ \left({T_{{\rm a}} -T_{\rm p}} \right)L}{E} \end{align} $ | (8) |
| $ \begin{align} {\Delta} L_{{\rm b}} &=\Delta l_{{\rm db}} +{\rm \Delta} l_{{\rm qb}} =8{\rm \Delta} s_{{\rm b}} +\frac{ \left({T_{{\rm b}} -T_{\rm p}} \right)L}{E} \end{align} $ | (9) |
其中
| $ \begin{equation} {\rm \Delta} L_{{\rm a}} +{\rm \Delta} L_{{\rm b}} =0 \end{equation} $ | (10) |
这样,关节2由于绳索的弹性形变而产生的转角偏移量分别可以由紧边或松边的总形变量计算得到:
| $ \begin{align} \Delta \theta_{2} &=\frac{{\rm \Delta} L_{{\rm a}}} {r}\\ &=\frac{8}{E\mu } \left({T_{{\rm a}} -T_{\rm p} -T_{\rm p} \ln \frac{T_{{\rm a}} }{T_{\rm p}}} \right)+\frac{ \left({T_{{\rm a}} -T_{\rm p}} \right)L}{Er} \end{align} $ | (11) |
或
| $ \begin{align} \Delta \theta_{2}& =\frac{{\rm \Delta} L_{{\rm b}}} {r}\\ &=-\frac{8}{E\mu } \left({T_{\rm p} -T_{{\rm b}} +T_{\rm p} \ln \frac{T_{{\rm b}} }{T_{\rm p}}} \right)-\frac{ \left({T_{{\rm b}} -T_{\rm p}} \right)L}{Er} \end{align} $ | (12) |
根据上述理论可知,在不考虑系统其他摩擦力的影响时,小臂因绳索的弹性形变而产生的转角偏移量与关节1的转角无关,而与绳索的拉力、绳索刚度、绳轮半径以及绳索与绳轮的摩擦系数有关。因此可以通过测量绳索的拉力来准确估计关节的转角偏移量,以提高控制精度[20]。
根据机械臂的传动特点可知,在平衡状态时,忽略系统内其他摩擦力的影响,驱动绳1和解耦绳1的自由段张力均为
假设初始位形下大、小臂为竖直状态(如图 5所示),
| $ \begin{equation} \left({T_{1} -T_{2}} \right)r=GL_{2} \cos \theta_{2} \end{equation} $ | (13) |
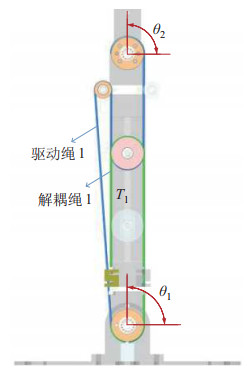
|
图 5 机械臂初始位形示意图 Fig.5 Illustration of the initial configuration of the manipulator |
考虑到关节2的弹性形变,有
| $ \begin{equation} \theta_{2} =q_{1} +q_{2} +\Delta \theta_{2} \end{equation} $ | (14) |
绳索的松边和紧边取决于
| $ \begin{equation} \begin{aligned} T_{{\rm a}}&=\max (T_{1}, T_{2}) \\ T_{{\rm b}}& =\min (T_{1}, T_{2}) \end{aligned} \end{equation} $ | (15) |
综上所述,将式(11) 或式(12) 与式(13)~(15) 联立,已知2根解耦绳的拉力
为验证该解耦机构的解耦效果,研制了2自由度绳驱动机械臂样机,如图 6所示。驱动系统包括直流无刷电动机(Deson motor 400276、Deson motor 360323,均含配套减速器)和电机驱动器(Copley Accelnet ACJ-090-12),关节2上装有17位绝对值编码器(多摩川TS5700 N8501),2根解耦绳均连接拉力传感器(LCLY-108 300N,精度0.03%)。机械臂所用的绳索为直径0.8 mm的不锈钢绳,导向轮直径为17 mm,其余绳轮直径均为34 mm,2对绳索自由段的总长度均为747.5 mm。

|
图 6 2自由度绳驱动机械臂样机 Fig.6 Prototype of the 2-DOF cable-driven manipulator |
为验证模型的正确性,首先需要辨识参数
| $ \begin{equation} \Delta \theta =\frac{1}{E\mu} \left({T-T_{\rm p} -T_{\rm p} \ln \frac{T}{T_{\rm p}}} \right)+\frac{ \left({T-T_{\rm p}} \right)l_{{\rm free}}} {Er} \end{equation} $ | (16) |
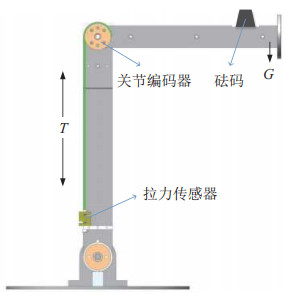
|
图 7 参数测量方法示意图 Fig.7 Illustration of the measurement of parameters |
式中绳轮半径
在本试验中去掉小臂,这样关节2就不受任何外力矩的作用,避免绳索弹性形变所产生的关节转角偏移。试验时的起始位形
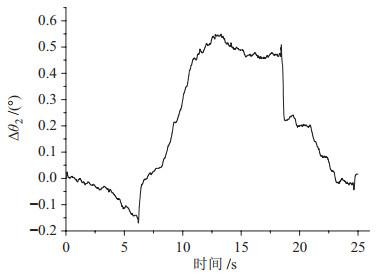
|
图 8 无外力矩时的关节解耦效果 Fig.8 Result of joint decoupling effect without external torque |
从图中可以看出,在此运动过程中关节2的转角偏移量变化比较小,变化幅值小于0.72°。从2.1节耦合现象的分析中可知,若未加入该解耦机构,关节2的耦合角度范围为
为证明解耦关节转角偏移模型的准确性,将机械臂调节至图 7所示位形,在小臂上增加砝码以调整关节2的外力矩,从而改变两端绳索的拉力,测量此时绳索的拉力与关节2的转角偏移量。总共测量3组试验,预紧力分别为30.97 N、38.32 N和41.75 N。试验时每次通过增加砝码改变的拉力大小为4.9 N。由于小臂的自重导致难以确定关节2力矩为0时编码器的数值,所以每组实验均以第1个数据为基准,设此时编码器数值为0。将紧边拉力
图 9显示3组初始预紧力下,紧边拉力
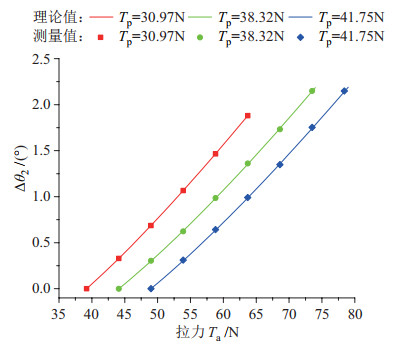
|
图 9 关节2的转角偏移试验结果 Fig.9 Experimental results of the angle offset of joint-2 |
本试验中大臂和小臂在初始位置下均为水平状态,关节1按梯形速度做0°—180° — 0°之间的往复运动,其中加减速时间均为4 s,匀速阶段的速度为17.70
观察图 10可以发现:
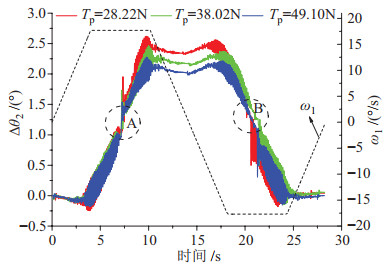
|
图 10 关节2动态解耦效果 Fig.10 Results of the dynamic decoupling effect of joint-2 |
(1) 机械臂关节1运动过程中关节2的转角偏移量会发生明显的变化,但是偏移量不超过3.0
(2) 关节2的转角偏移量会发生周期性的抖动,尤其是匀速运行阶段,这是由于关节2的动态弹性形变导致的;
(3) 随着预紧力增大,机械臂关节2的转角偏移量减小;
(4) 在A、B区域,关节2的转角偏移量发生明显突变,此时对应的
根据上述试验结果可知,提出的解耦方法的解耦效果良好,也验证了关节转角偏移模型的准确性。通过测量绳索拉力,并结合关节转角偏移模型,不仅可以准确估计关节的转角偏移量,同时也可以得到关节所受力矩,因此在精度要求不高的应用场合中可以不使用关节编码器和扭矩传感器。
为了实现机械臂精确的运动控制,获得理想的定位精度,则需要更换高性能减速器,同时应用鲁棒的减振控制算法消除抖动。
5 结论(Conclusion)(1) 本文对绳驱动机械臂关节运动耦合现象进行了分析,提出了一种采用通过动滑轮补偿关节运动耦合量,从而实现绳驱动关节运动解耦的方法。
(2) 基于解耦原理,研制了一种2自由度绳驱动机械臂。进而分析了绳索的弹性形变对关节解耦效果的影响,建立了关节转角偏移理论模型。
(3) 通过试验验证了提出的解耦机构的有效性,以及关节转角偏移模型的准确性,同时显示关节转角偏移量同紧边拉力
(4) 机械臂的动态测试试验结果表明机械臂关节的动态解耦性能良好,但为了实现高精度定位,后续需要应用鲁棒的减振控制算法。
| [1] |
Grosu S, de Rijcke L, Grosu V, et al. Driving robotic exoskeletons using cable-based transmissions: A qualitative analysis and overview[J]. Applied Mechanics Reviews, 2018, 70(6). DOI:10.1115/1.4042399 |
| [2] |
Perry J C, Rosen J, Burns S. Upper-limb powered exoskeleton design[J]. IEEE/ASME Transactions on Mechatronics, 2007, 12(4): 408-417. DOI:10.1109/TMECH.2007.901934 |
| [3] |
Kirchhoff J. Towards dependability of ultra lightweight tendon driven series elastic robots[D]. Darmstadt, Germany: The Technical University of Darmstadt, 2018.
|
| [4] |
Kirchhoff J, Stryk O V. Velocity estimation for ultra lightweight tendon driven series elastic robots[J]. IEEE Robotics and Automation Letters, 2018, 3(2): 664-671. DOI:10.1109/LRA.2017.2729663 |
| [5] |
Lens T, Kunz J, Stryk O V, et al. BioRob-arm: A quickly deployable and intrinsically safe, light-weight robot arm for service robotics applications[C]//41st International Symposium on Robotics and 6th German Conference on Robotics. Piscataway, USA: IEEE, 2010: 1-6.
|
| [6] |
陈伟海, 游贤强, 崔翔, 等. 绳驱动拟人臂机器人的动力学建模及张力分析[J]. 北京航空航天大学学报, 2013, 39(3): 335-339. Chen W H, You X Q, Cui X, et al. Dynamics modeling and tension analysis for a cable-driven humanoid-arm robot[J]. Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(3): 335-339. |
| [7] |
陈伟海, 陈竞圆, 崔翔, 等. 绳驱动拟人臂机器人的刚度分析和优化[J]. 华中科技大学学报: 自然科学版, 2013, 41(2): 12-16. Chen W H, Chen J Y, Cui X, et al. Stiffness analysis and optimization of a novel cable driven anthropomorphic-arm manipulator[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2013, 41(2): 12-16. |
| [8] |
王建华, 刘素庆, 陈伟海. 具有关节角反馈的绳驱动仿人肩关节的张力优化与控制[J]. 机器人, 2011, 33(3): 324-331. Wang J H, Liu S Q, Chen W H. Tension optimization and control of a cable-driven humanoid shoulder with joint angle feedback[J]. Robot, 2011, 33(3): 324-331. |
| [9] |
Townsend W T, Guertin J A. Teleoperator slave-WAM design methodology[J]. Industrial Robot, 1999, 26(3): 167-177. DOI:10.1108/01439919910266820 |
| [10] |
Lioulemes A, Theofanidis M, Kanal V, et al. MAGNI dynamics: A vision-based kinematic and dynamic upper-limb model for intelligent robotic rehabilitation[J]. International Journal of Biomedical and Biological Engineering, 2017, 11(4): 158-167. |
| [11] |
Zhao B L, Nelson C A. Decoupled cable-driven grasper design based on planetary gear theory[J]. Journal of Medical Devices, 2013, 7(2). DOI:10.1115/1.4024329 |
| [12] |
蒋素荣. 绳驱动机械臂解耦方法与鲁棒控制研究[D]. 南京: 南京航空航天大学, 2018. Jiang S R. Research on motion-decoupling methods and robust control of cable-driven manipulator system[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2018. |
| [13] |
Jiang S R, Hua D R, Wang Y Y, et al. Design and modeling of motion-decoupling mechanism for cable-driven joints[J]. Advances in Mechanical Engineering, 2018, 10(5). DOI:10.1177/1687814018777428 |
| [14] |
Kim Y J. Anthropomorphic low-inertia high-stiffness manipulator for high-speed safe interaction[J]. IEEE Transactions on Robotics, 2017, 33(6): 1358-1374. |
| [15] |
Kim Y J, Kim J I, Jang W. Quaternion joint: Dexterous 3-DOF joint representing quaternion motion for high-speed safe interaction[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2018: 935-942.
|
| [16] |
Scarcia U, Melchiorri C, Palli G. Towards simplicity: On the design of a 2-DOFs wrist mechanism for tendon-driven robotic hands[C]//IEEE International Conference on Robotics and Biomimetics. Piscataway, USA: IEEE, 2015: 1317-1322.
|
| [17] |
Lee J K, Choi C H, Yoon K H, et al. Design of a servo manipulator with tendon transmission[C]//International Conference on Control, Automation and Systems. Piscataway, USA: IEEE, 2008: 1653-1656.
|
| [18] |
Shah D, Parmiggiani A, Kim Y J. Constant length tendon routing mechanism through axial joint[C]//IEEE/ASME International Conference on Advanced Intelligent Mechatronics. Piscataway, USA: IEEE, 2020: 753-758.
|
| [19] |
Baser O, Konukseven E I. Theoretical and experimental determination of capstan drive slip error[J]. Mechanism and Machine Theory, 2010, 45(6): 815-827. DOI:10.1016/j.mechmachtheory.2009.10.013 |
| [20] |
Chen L, Wang X S, Xu W L. Inverse transmission model and compensation control of a single-tendon-sheath actuator[J]. IEEE Transactions on Industrial Electronics, 2014, 61(3): 1424-1433. |
 2022, Vol. 44
2022, Vol. 44


