1 引言（Introduction）

可变形移动机器人具有特殊的结构设计，可以根据需要改变自身构形，从而在非结构化场景中完成一些复杂的作业任务，例如外星探测、人员救援、危险废弃物清理等^[1-3]。典型的可变形移动机器人包括哈尔滨工业大学研发的UBot^[4]，瑞士仿生机器人实验室研发的Roombots^[5]以及英国谢菲尔德大学研发的HyMod^[6]等。目前，相关研究主要集中在机器人系统开发。该类机器人虽已具有构形变换的潜能，但是普遍缺乏改变构形的依据和规划方法。

构形变换是机器人从当前构形变换至目标构形的过程，其关键问题之一就是选择合适的目标构形，因而需采用合理的指标对机器人不同构形进行评价，将评价结果作为选择的依据。文[7]研究和对比了不同构形的地面移动机器人的运行性能，主要讨论了运行特性（动力性指标：平均速度、加速度；平稳性指标：最大和最小加速度差）和通过性（能否通过某一给定路段）两类指标，不涉及机器人构形的变化。文[8]针对地震辅助救援四足机器人提出了生存能力、运动能力、作业能力以及环境交互能力几项指标，通过分析评价数据指出了四足机器人在设计上的一些不足。文[9]定量分析和对比了可变形机器人不同构形的转向能力，但未对其他指标进行研究。从环境适应性角度来看，目标构形优选是基于评价结果从构形集合中选择与环境特征最匹配的构形。由于缺乏合理的构形评价指标及结果作为依据，目前还没有关于移动机器人构形优选的相关研究。

构形之间的变换路径规划也是机器人构形变换的关键问题之一。Zhao等^[10]以构形相似度作为机器人构形变换规划的搜索驱动函数，提出了以较少变换步骤为目标的路径搜索方法。以4个可重构模块组成的地面移动清洁机器人为对象，文[11]研究并绘制了机器人7种构形之间重构变换的能耗矩阵，通过仿真与实验验证了在机器人清扫地板过程中考虑构形重构能耗的意义。构形变换路径规划既要考虑运动约束下的变换可行性，也要考虑变换空间、能耗和效率等综合指标。

综上所述，目前构形可变移动机器人缺乏构形评价参考依据，构形优选难以开展，构形变换路径规划方法也有所欠缺。针对上述不足，本文提出一种适用于构形可变轮式移动机器人的构形评价、优选和变换路径规划方法。首先，列举构形可变移动机器人Mobot-VC（modular wheeled mobile robot with variable configurations）的主要构形，提出构形的分类方法和评价指标；然后构建多目标优化模型，实现根据环境特征优选合适的构形；再建立以构形为节点、变换可行性为边、变换能耗为权的构形变换网络图，将构形变换路径规划转化为网络路径搜索问题，从而求解任意两构形间耗能最少的变换路径。最后，通过实验验证本文方法的合理性和有效性。研究方法及结果可为此类构形可变轮式移动机器人的设计分析和运动规划提供指导或参考。

2 机器人及其运动学模型（The robot and its kinematic model) 2.1 机器人系统

如图 1所示，本文研究对象为一种车体构形、轮距和轮向可变的新型轮式移动机器人Mobot-VC。该机器人采用模块化方法搭建，由6个关节模块、2个轮子模块和1个小脚轮构成。关节模块包括I型（回转）关节和T型（摆转）关节2种。其中I型关节的关节轴线与转动轴重合，T型关节的关节轴线则与转动轴垂直。具体而言，机器人躯体中部的4个T型关节的关节轴线互相平行，用于改变车体构形、轮距和轮向；两端各布置一个I型关节，作为轮子模块的驱动单元；小脚轮固定安装于机器人车体中间连杆中点的下方，用于支撑机器人的躯体，使之不直接触地。

Mobot-VC机器人的主控制器为工控机，操作系统为ROS（robot operation system）。上述每个关节模块均集成了电机、编码器和伺服控制器。机器人控制采用分布式架构，主控制器通过USB-to-CAN方式与每个关节模块的伺服控制器通信，实现每个关节模块的运动伺服控制^[12]。本文构形优选和变换路径规划算法在机器人主控制器中运行。

2.2 运动建模

由于小脚轮为被动轮，且其运动在理论上对机器人变构形运动不产生影响，因此在运动分析过程中可忽略小脚轮的运动。如图 2所示，在机器人车体中间连杆中心（小脚轮处）建立坐标系。图中$ q_{i} $（$ i=1, 2, \cdots, 6 $）为各关节角，$ l_{0} $、$ l_{1} $ 和$ l_{2} $ 为各连杆长度，$ {{\mathit{\boldsymbol{u}}}}_{j} $（$ j=1, 2 $）为轮子模块的位姿。由机器人运动学推导公式可得轮子模块的位姿^[13]为

$ \begin{align} {{\mathit{\boldsymbol{u}}}}_{j} =\begin{bmatrix} {x_{j}} \\ {y_{j}} \\ {\theta_{j}} \end{bmatrix} =\begin{bmatrix} {l_{1} \cos {q_{2j+1}}+l_{2} \cos ({q_{2j+1} +q_{2j+2}})} \\ {\dfrac{l_{0}} {2}\!+\!l_{1} \sin {q_{2j+1}}\!+\!l_{2} \sin ( {q_{2j+1} \!+\!q_{2j+2}})} \\ {q_{2j+1} +q_{2j+2} +\dfrac{\rm{\pi }} {2}} \end{bmatrix} \end{align} $

(1)

式中，$ {{\mathit{\boldsymbol{u}}}}_{1} $ 和$ {{\mathit{\boldsymbol{u}}}}_{2} $ 分别是关于$ q_{3} $、$ q_{4} $ 及$ q_{5} $、$ q_{6} $ 的函数。

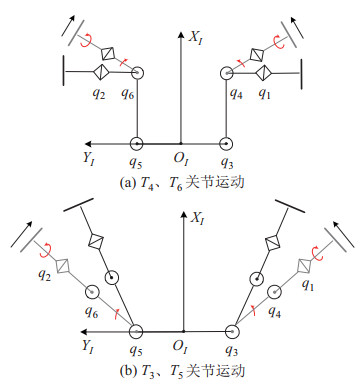
当机器人4个T型关节的角度发生改变，车体形状、相应的轮距（两轮子模块中心点之间距离）和轮向（轮子模块的方位）均会发生变化。而轮式移动机器人运动必须满足非完整约束，即轮子与地面之间只有纯滚动而没有相对滑动。因此，如图 3所示，图 3(a)中关节运动应满足以下速度约束：

$ \begin{align} \begin{cases} \dot{q}_{3} =0, &\dot{q}_{4} \cdot l_{2} =\dot{q}_{1} \cdot r_{\rm w} \\ \dot{q}_{5} =0, &\dot{q}_{6} \cdot l_{2} =\dot{q}_{2} \cdot r_{\rm w} \end{cases} \end{align} $

(2)

图 3(b)中关节运动应满足：

$ \begin{align} \begin{cases} q_{4} =0, &\dot{q}_{3} \cdot ({l_{1} +l_{2}})=\dot{q}_{1} \cdot r_{\rm w} \\ q_{6} =0, &\dot{q}_{5} \cdot ({l_{1} +l_{2}})=\dot{q}_{2} \cdot r_{\rm w} \end{cases} \end{align} $

(3)

其中，$ r_{\rm w} $ 为轮子模块半径。

2.3 构形分类

记机器人某一构形为$ c_{i} $，则其构形集合可表示为$ C=\{{c_{i} |i=1, 2, 3, \cdots, m} \} $。本文将所研究的机器人构形依据两轮子模块轴线的几何关系划分为3大类：轮轴共线$ C_{\rm Co} $、轮轴平行$ C_{\rm Pa} $ 以及轮轴相交$ C_{\rm In} $。设两轮子模块的轴线方程分别为$ a_{1} x+b_{1} y+n_{1} =0 $ 及$ a_{2} x+b_{2} y+n_{2} =0 $，则构形分类条件为

$ \begin{align} c_{i} \in \begin{cases} C_{\rm Co}, & D\ne 0 \\ C_{\rm Pa}, & D=0, D_{\rm x} \ne 0\rm{ 或}\; D=0, D_{\rm y} \ne 0 \\ C_{\rm In}, & D=D_{\rm x} =D_{\rm y} =0 \end{cases} \end{align} $

(4)

式中，

$ \begin{align*} D=\begin{vmatrix} {a_{1}} & {b_{1}} \\ {a_{2}} & {b_{2}} \end{vmatrix}, \; D_{\rm x} =\begin{vmatrix} {-n_{1}} & {b_{1}} \\ {-n_{2}} & {b_{2}} \end{vmatrix}, \; D_{\rm y} =\begin{vmatrix} {a_{1}} & {-n_{1}} \\ {a_{2}} & {-n_{2}} \end{vmatrix} \end{align*} $

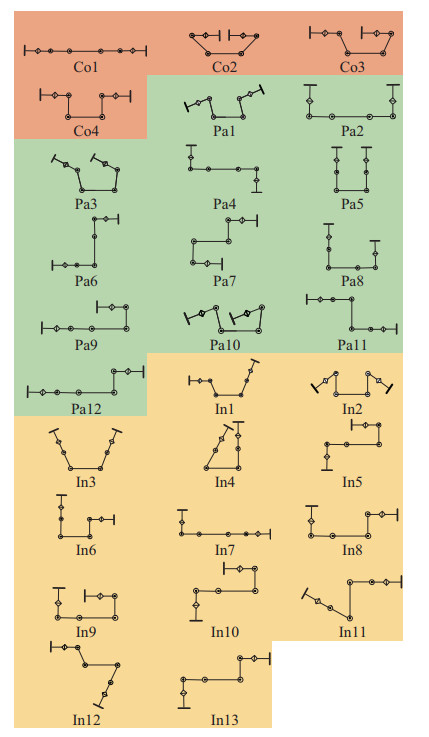
在上述三大类构形基础上还可细分出更多的构形。根据T型关节角取值分别为$ 0^{\circ} $、$ \pm 45^{\circ} $、$ \pm 90^{\circ} $ 和$ \pm 135^{\circ} $，可列举机器人的构形集合，去掉对称以及形态相同的构形后，机器人Mobot-VC的主要构形如图 4所示。由非完整运动约束可知，轮轴共线类构形的机器人可直行或转向，轮轴平行类构形的机器人只可直行，而轮轴相交类构形的机器人只可转向。

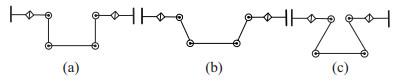
此外，如图 5所示，同一种构形下，机器人的轮距和轮向可以不相同。

3 构形评价（Configuration evaluation）

不同构形的机器人具有不同的移动性和稳定性，本文采用3个指标进行分析和评价：1) 转弯所需半径$ r $，决定机器人移动的灵活性；2) 宽度$ h $，决定机器人可否通过给定的通道；3) 稳定角$ \phi $，决定机器人在移动过程中的稳定性。

3.1 转弯所需半径

移动机器人转弯时需要一定的空间大小，如图 6所示，机器人转弯时可视为绕某个点整体转动。其中旋转中心的坐标$ ({x_{A}, y_{A}} $) 可通过联立两轮子模块轴线方程计算交点获得。而两轮子模块的坐标由式(1) 可得，其到旋转中心的距离为

$ \begin{align} d_{j} =\sqrt{({x_{j} -x_{ A}})^{2}+({y_{j} -y_{ A}})^{2}}, \; \; {j=1, 2} \end{align} $

(5)

式中，不同构形情况下旋转中心的坐标取值分别为

$ \begin{align*} \begin{cases} (\infty, \infty), & \; c_{i} \in C_{\rm Pa} \\ ({x_{j}, 0}), & \; c_{i} \in C_{\rm Co} \\ ({x_{ A}, y_{ A}}), &\; c_{i} \in C_{\rm In} \end{cases} \end{align*} $

取两轮子模块到旋转中心更远的距离作为机器人转弯所需的半径：

$ \begin{align} r=\max \{d_{1}, d_{2}\} \end{align} $

(6)

3.2 通过宽度

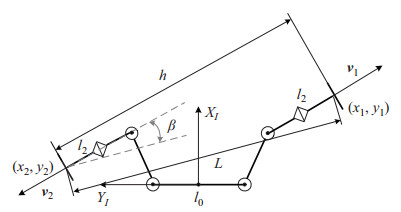
根据图 7可知，最小通过宽度的计算公式为

$ \begin{align} h=L\cos\beta +\sigma l_{2} \end{align} $

(7)

式中，$ L=\sqrt{({y_{2} -y_{1}})^{2}+({x_{2} -x_{1}})^{2}} $ 为机器人轮子模块中心点的连线长度；$ \beta \in [0, 90^{\circ}] $ 为轮子模块中心点的连线与通道截面的夹角；$ \sigma $ 为不同构形的轮距系数，取

$ \sigma= \begin{cases}1, & \boldsymbol{v}_{1}=\boldsymbol{v}_{2} \text { 且 } \boldsymbol{v}_{1} \cdot \boldsymbol{v}_{2}>0 \\ 2, & \boldsymbol{v}_{1}=\boldsymbol{v}_{2} \text { 且 } \boldsymbol{v}_{1} \cdot \boldsymbol{v}_{2} < 0 \text { 且 } L < l_{0} \\ 0, & \text { 其他 }\end{cases}$

(8)

式中，$ {\mathit{\boldsymbol{v}}}_{1} $ 和$ {\mathit{\boldsymbol{v}}}_{2} $ 为轮轴轴线的单位方向向量。

3.3 稳定角

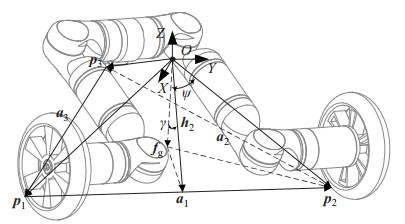
本文采用稳定锥方法^[14-15]分析机器人沿边线、角点倾翻的临界角（简称稳定角），以此评价机器人在移动过程中的稳定性。如图 8所示，取轮子与地面的接触点为稳定锥底面的角点，并记其坐标为$ {\mathit{\boldsymbol{p}}}_{i} $（$ i=1, 2, 3 $）；取机器人质心为稳定锥的顶点，并在顶点建立如图 8所示的坐标系，记重心向量为$ {\mathit{\boldsymbol{f}}}_{\rm g} $。则稳定锥底面边线为

$ \begin{align} {\mathit{\boldsymbol{a}}}_{i} =\begin{cases} {{\mathit{\boldsymbol{p}}}_{i+1} -{\mathit{\boldsymbol{p}}}_{i}, } & {i=1, 2} \\ {{\mathit{\boldsymbol{p}}}_{1} -{\mathit{\boldsymbol{p}}}_{i}, } & {i=3} \end{cases} \end{align} $

(9)

过重心且与稳定锥底面边线垂直的向量为

$ \begin{align} \mathit{\boldsymbol{h}}_{i} =(1-\overset\frown{\mathit{\boldsymbol{a}}}_{i} \cdot \overset\frown{\mathit{\boldsymbol{a}}}_{i}^{\rm T}) \mathit{\boldsymbol{p}}_{i+1} \end{align} $

(10)

式中，$ \overset\frown{\mathit{\boldsymbol{a}}}_{i} =\mathit{\boldsymbol{a}}_{i} /\| \mathit{\boldsymbol{a}}_{i} \| $。则与边线对应的倾翻角为

$ \begin{align} \gamma_{i} = \lambda_{i} \arccos(\overset\frown{\mathit{\boldsymbol{f}}}_{ \rm g} \cdot \overset\frown{\mathit{\boldsymbol{h}}}_{i}), \quad i=1, 2, 3 \end{align} $

(11)

式中，$ \lambda_{i} =\begin{cases} {+1, } & (\overset\frown{\mathit{\boldsymbol{f}}}_{\rm g} \times \overset\frown{\mathit{\boldsymbol{h}}}_{i})\cdot \overset\frown{\mathit{\boldsymbol{a}}}_{i} < 0 \\ {-1, } & \rm{其他} \end{cases} $。

同理，与角点对应的倾翻角为

$ \begin{align} \psi_{i} = \varepsilon_{i} \arccos(\overset\frown{\mathit{\boldsymbol{f}}}_{\rm g} \cdot \overset\frown{\mathit{\boldsymbol{p}}}_{i}), \quad i=1, 2, 3 \end{align} $

(12)

式中，

$ \begin{align} \varepsilon_{i} =\begin{cases} {+1, } & (\overset\frown{\mathit{\boldsymbol{f}}}_{\rm g} \!\times\! \overset\frown{\mathit{\boldsymbol{h}}}_{i})\cdot \overset\frown{\mathit{\boldsymbol{a}}}_{i} <0 \rm{ 或}\; (\overset\frown{\mathit{\boldsymbol{f}}}_{\rm g} \!\times\! \overset\frown{\mathit{\boldsymbol{h}}}_{i+1})\cdot \overset\frown{\mathit{\boldsymbol{a}}}_{i+1} <0 \\ {-1, } & \rm{其他} \end{cases} \end{align} $

(13)

考虑机器人的全局稳定性，取稳定锥边线或角点所对应的倾翻临界角最小值作为稳定角，即有：

$ \begin{align} \phi =\min (\psi_{i}, \gamma_{i}), \; \; {i=1, 2, 3} \end{align} $

(14)

4 构形优选（Configuration selection）

将每个机器人构形与上述3个指标评价结果关联，可得构形元组$ \{{c_{i}, h, r, \phi} \} $，其中$ h $ 代表根据式(7) 计算的通过宽度，$ r $ 代表根据式(6) 获得的转弯所需半径，$ \phi $ 代表根据式(14) 获得的稳定角。

若给定环境信息，如过道宽度$ H $、无障碍空间半径$ R $ 以及路面倾角$ \alpha $，运用多目标优化模型，即可选择与环境匹配的机器人构形。利用权系数法建立多目标优化模型：

$ \begin{align} &\min F=\omega_{1} (-h)+\omega_{2} r+\omega_{3} (-\phi) \end{align} $

(15)

$ \begin{align} &\rm{s.t.}\; \begin{cases} {0<h<H} \\ {\dfrac{H}{2}<r<R} \\ {\alpha <\phi <90^{\circ}} \end{cases} \end{align} $

(16)

式中，$ \omega_{j} $ 为权重，$ \sum\limits_{j=1}^3 {\omega_{j} =1} $，可采用熵权法^[16]来确定。各评价指标的信息熵可表示为

$ \begin{align} e_{j} =-\frac{1}{\ln m}\sum\limits_{i=1}^m {p_{ij} \ln p_{ij}} \end{align} $

(17)

式中，$ p_{ij} =x_{ij} \Bigm/ \sum\limits_{i=1}^m {x_{ij}} $，$ m $ 为构形个数，$ x_{ij} $ 为采用最小—最大规范化方法处理后的评价结果。进而，各指标权重为

$ \begin{align} \omega_{j} =\frac{1-e_{j}} { \sum\limits_{k=1}^3 {({1-e_{k}})}} \end{align} $

(18)

5 构形变换规划（Configuration transformation planning）

一方面，由于轮子模块存在纯滚动约束，机器人并不能实现任意两构形间的直接变换，过程中可能需要经过一些中间过渡构形。另一方面，两构形间变换也可能存在多种中间过渡构形可供选择的情况。为解决上述问题，本节提出一种基于加权网络模型的构形变换规划方法。

5.1 加权网络模型的构建

为将构形变换规划转化为网络路径搜索问题，构建以构形为节点、变换可行性为边、变换能耗为权的网络模型$ G $^[17]：

$ \begin{align} G&=({C, E}) \end{align} $

(19)

$ \begin{align} \mathit{\boldsymbol{W}} &=\begin{bmatrix} {w_{11}} & {w_{12}} & \cdots & {w_{1m}} \\ {w_{21}} & {w_{22}} & \cdots & {w_{2m}} \\ \vdots & \vdots & \ddots & \vdots \\ {w_{m1}} & {w_{m2}} & \cdots & {w_{mm}} \end{bmatrix} \end{align} $

(20)

$ \begin{align} w_{ij} &=\begin{cases} {0, } & {i=j} \\ {T_{ij}, } & i\ne j \rm{ 且}\; (c_{i}, c_{j})\in E \\ {\infty, } & i\ne j \rm{ 且}\; (c_{i}, c_{j})\notin E \end{cases} \end{align} $

(21)

式中，$ C=\{{c_{1}, c_{2}, \cdots, c_{m}} \} $ 为构形集合，$ E $ 为边的集合；$ \mathit{\boldsymbol{W}} $ 为能耗矩阵，其元素$ w_{ij} $ 表示边$ (c_{i}, c_{j} $) 的权，$ T_{ij} $ 为从构形$ c_{i} $ 变换到构形$ c_{j} $ 所需的能耗。

5.2 构形变化的能耗

构形可变移动机器人的构形由4个T型关节决定。因此，分析构形变换所需能耗时只计算4个T型关节的能耗。机器人的动力学方程一般形式为

$ \begin{align} {\mathit{\boldsymbol{\tau}}} ={\mathit{\boldsymbol{H}}}({\mathit{\boldsymbol{q}}})\mathit{\boldsymbol{\ddot{q}}}+{\mathit{\boldsymbol{C}}}({\mathit{\boldsymbol{q}}}, \mathit{\boldsymbol{\dot{q}}})\mathit{\boldsymbol{\dot{q}}}+{\mathit{\boldsymbol{G}}}({\mathit{\boldsymbol{q}}}) \end{align} $

(22)

式中，$ {\mathit{\boldsymbol{q}}} $、$ \mathit{\boldsymbol{\dot{q}}} $、$ \mathit{\boldsymbol{\ddot{q}}} $ 分别为关节角度、角速度和角加速度向量；$ {\mathit{\boldsymbol{H}}}({\mathit{\boldsymbol{q}}} $) 为惯性矩阵，$ {\mathit{\boldsymbol{C}}}({\mathit{\boldsymbol{q}}}, \mathit{\boldsymbol{\dot{q}}} $) 为哥氏力和离心力矩阵，$ {\mathit{\boldsymbol{G}}}({\mathit{\boldsymbol{q}}} $) 为重力矢量。

机器人在构形变换过程中所消耗的能量为^[18]

$ \begin{align} T=\sum\limits_{i=3}^6 \int_{t_{0}}^{t'} {\tau_{i}^{2}} {\rm d} t \end{align} $

(23)

式中，$ \tau_{i} $ 表示$ i $ 关节的关节力矩（关节序号与图 2对应），$ t_{0} $ 和$ {t}' $ 分别表示$ i $ 关节运动的起始时间和结束时间。

5.3 基于能耗最小的构形变换规划

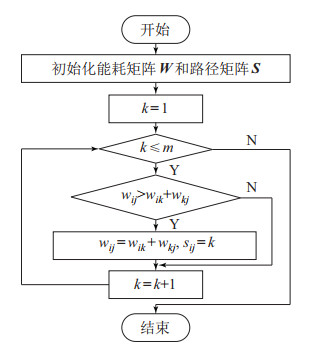
对于有权网络模型任意两节点间最短路径的搜索问题，可以采用Floyd算法^[19]（又称为插点法）一次性获得任意起点到任意终点的最短路径集合。算法流程如图 9所示。其主要步骤为：

(1) 根据式(20) 和式(21) 构造有权网络模型的能耗矩阵$ \mathit{\boldsymbol{W}}=[w_{ij}]_{m\times m} $ 和路径矩阵$ \mathit{\boldsymbol{S}}=[s_{ij}]_{m\times m} $，并初始化$ s_{ij} =j $。

(2) 尝试把节点$ k $ 插入到节点$ i $ 和节点$ j $ 之间；若插入节点后构形变换能耗更少，则更新能耗矩阵元素$ w_{ij} =w_{ik} +w_{kj} $ 和路径矩阵元素$ s_{ij} =k $。

(3) 遍历所有节点（$ k=1, \cdots, m $，$ i=1, \cdots, m $，$ j $ $ = $ $ 1, \cdots, m $），重复执行步骤(2)，得到路径矩阵$ \mathit{\boldsymbol{S}} $ 及对应的能耗矩阵$ \mathit{\boldsymbol{W}} $。任意两节点间能耗最少的变换路径即可通过查询$ \mathit{\boldsymbol{S}} $ 和$ \mathit{\boldsymbol{W}} $ 获得。

6 实验与分析（Experiments and analysis） 6.1 构形评价分析

本文选取图 4中12种构形作为评价分析的示例，评价结果如表 1所示。将各指标计算结果进行最小—最大规范化后绘制出不同构形的性能雷达图，如图 10所示。

根据图 10(a)~(c)可知，轮轴共线构形的综合性能（雷达图面积）排名为：Co4 $ > $ Co3 $ > $ Co2 $ > $ Co1；轮轴平行构形的综合性能排名为：Pa2 $ > $ Pa3 $ > $ Pa1 $ > $ Pa4；而轮轴相交构形的综合性能排名为：In4 $ > $ In1 $ > $ In2 $ > $ In3。将各类别构形中综合性能最好的评价结果绘于一个雷达图中，得到图 10(d)。分析图 10(d)结果可得：

(1) 构形In4相较其他2种构形稳定性好，而另外2种指标性能较差。该类构形可实现绕任意点稳定地做回转运动。

(2) 构形Pa2的通过宽度最小，稳定性较好，可通过较窄环境。

(3) 构形Co4转弯所需半径最小，不仅综合性能最优，同时拥有灵活多变的运动方式。

6.2 构形变换能耗实验

为验证能耗计算模型的正确性，采集机器人按照指定构形进行变换时的各关节电流、电压以及所用时间，通过式(24) 计算实施该构形变换所消耗的能量：

$ \begin{align} {T}'=\sum\limits_{i=3}^6 {| {UI_{i} t_{i}} |} \end{align} $

(24)

式中，$ U $ 为电压，$ I_{i} $ 和$ t_{i} $ 分别为$ i $ 关节的电机电流及运动时间（关节序号与图 2对应）。

本文组织了4组实验。每组随机选取2种构形，通过式(23) 计算变换所需的理论能耗，并在实验中通过式(24) 获取变换的实际能耗，结果如表 2所示。4组实验中，构形变换对应的能耗误差约为$ - $10{%}。误差主要来源于理论计算时忽略了摩擦以及地形高低等影响。该实验说明式(23) 可作为构形变换规划所需能耗的计算依据。

6.3 构形优选及变换规划仿真

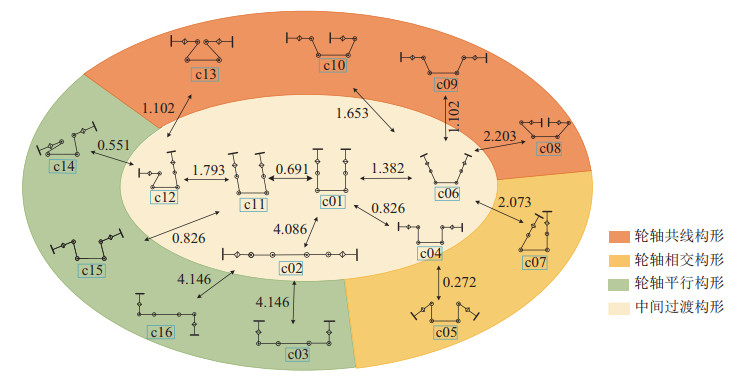
从图 4中选取部分代表构形，根据非完整运动约束增加必要的中间过渡构形，绘制了如图 11所示的构形变换网络图。图 11中，节点为机器人的构形，节点间边的连通性表示两构形可相互变换，边的权值为构形变换的理论能耗；内圈为中间过渡构形，外圈按轮轴共线、轮轴平行和轮轴相交划分为3个区域，分别用不同颜色标识。图中的任意2个构形都可利用构形变换规划算法得到构形之间变换的过渡路径，且图中任意一个构形都可作为构形规划的起始构形或目标构形。

本文利用Matlab编写了算法及其界面，用于机器人的构形优选及变换规划，如图 12所示。图 12(a)为将环境信息$ (135, \; 60, \; 0) $ 输入构形优选算法界面，得到对应的优选构形c04；图 12(b)为输入2个构形$ (c4, \; c3) $ 至构形变换规划界面，得到构形间变换能耗最小的路径为c04 $ \to $ c01 $ \to $ c02 $ \to $ c03。

6.4 构形优选及变换规划实验

为展示Mobot-VC机器人在本文方法的支持下能够通过改变构形提升其环境适应性，搭建了如图 13所示的测试环境。该实验环境划分为A~D四部分（见图 13中不同颜色的阴影线），各部分的结构参数见表 3。为获取机器人运动的实际轨迹，在机器人躯体中心、两端I型关节模块（非旋转部分）分别安装标记，利用运动捕捉系统（OpticTrack，工作范围8 m$ \times $7 m$ \times $3 m，名义追踪精度0.1 mm）进行多标记点追踪。

实验开始前给定环境信息，采用传统机器人路径规划算法获得从A区到D区的运动路径；然后根据环境结构参数通过构形优选，得到机器人在各段路径中的匹配构形；再采用构形变换规划方法分别获得两两构形之间的变换路径；最后一一插补满足式(2) 和式(3) 的构形变换运动，从而获得机器人从A区到D区的整段运动轨迹。

图 14为机器人在构形优选及变换规划运动实验中的视频截图，从图中可知，机器人能根据给定的环境结构参数优选出合适构形，例如通过C区狭窄通道、爬上D区斜坡时保持稳定性等。若不变换构形，机器人将无法通过C区狭窄通道。图 15所示为机器人各部分的运动轨迹，从图中可见，机器人进行了4次构形变换，以适应各区域的环境；机器人躯体中心实际运动轨迹与规划相符，但存在明显的误差累积现象。累积误差的主要原因：机器人两端重量不对称导致两轮子模块与地面摩擦不一致，小脚轮的万向调节功能欠佳导致非轮向摩擦。该实验说明机器人能够使用优选的构形及规划的构形变换运动安全、无碰地通过给定环境。

7 总结（Conclusion）

构形可变是本文所研究的机器人系统的特色和优点之一。根据环境结构优选构形并进行构形变换规划，是提升该类机器人环境适应性的有效途径。

本文从构形评价、构形优选及构形变换规划3个方面进行了分析和研究，提出了适用于构形可变移动机器人的构形变换规划方法。计算分析表明，轮轴共线构形Co4在示例的构形当中综合性能最好；仿真和实验验证了可结合环境特征和构形评价结果进行构形优选，且将构形变换路径规划问题转换为网络路径搜索来解决是可行的；所提出的评价指标和构形变换规划方法可用于这类移动机器人的设计分析和运动规划，提升其环境适应性。

由于篇幅所限，本文仅给出了3个构形评价指标，但所提分析思路、构形优选及变换规划方法易于增加更多评价指标，例如瞬时加速性能、制动性能和爬坡性能等^[20]。下一步将为机器人增加环境传感器，研究机器人在线感知环境及同时进行构形变换规划和移动路径规划的问题。