1 引言（Introduction）

近年来可穿戴式设备受到世界各研究机构的重视并得到广泛研究，为了提高其人机相容性及安全性，各研究机构开始采用气动人工肌肉作为可穿戴式设备的驱动器^[1]。与传统的刚性驱动器相比，气动人工肌肉驱动器通过改变自身形状进行收缩或伸长，具有结构简单、质量轻、功率密度大、动作平滑、安全等突出优势^[2]，这些优点使其在穿戴式设备中具有广泛的应用前景^[3]。

20世纪中叶美国医生McKibben最早提出了气动人工肌肉的概念，发明了最早的McKibben气动人工肌肉^[4]。随着材料技术、制造工艺的发展，各研究机构研发了各种类型的人工肌肉驱动器，如采用新型编织工艺的气动人工肌肉^[5-11]、Peano扁平气动人工肌肉^[12-16]、真空驱动的气动人工肌肉^[16-19]、“菱形”气动人工肌肉^[20-21]以及采用新材料技术的Peano电致伸缩驱动器^[22]等。

比较典型的采用新型编织工艺的气动人工肌肉有：褶皱型气动人工肌肉^[5]、改进编织工艺的McKibben气动人工肌肉^[6]、扁平状的纤维硅胶复合气动人工肌肉^[7]、编织型的“18Weave”气动人工肌肉^[8]、采用激光切割的“缝隙管”气动人工肌肉^[9-10]。这类气动人工肌肉通过采用各种新型的编织工艺以及新型制造工艺来制造约束纤维或约束层。但是驱动部件仍然是以橡胶和硅胶为代表的传统的弹性驱动器。新编织工艺在一定程度上改善了气动人工肌肉的收缩特性，然而未能有效提高其收缩率。

比较典型的Peano气动人工肌肉是将2层薄膜焊接在一起^[23]，形成一个具有多腔室的“气袋”，通过向气袋内充入压缩气体实现气动人工肌肉的收缩。这类气动人工肌肉的结构简单，并且部分Peano气动人工肌肉采用了纤维增强，因此具有较大的收缩力，但是其收缩率较低。

为了提高收缩率，部分学者提出了采用波纹管结构^{[17, 24]}或折纸结构^[18-19]的真空收缩气动人工肌肉。通过采用真空泵在气动人工肌肉内部形成接近真空的负压，在大气压的驱动下，气动人工肌肉可沿着长度方向收缩，从而获得极高的收缩率。然而，气动人工肌肉的内外压差无法超过标准大气压力，因此收缩力受到一定限制。为了提高驱动能力，往往采用增大气动人工肌肉截面面积的方法，但这会增大气动人工肌肉的体积。

“菱形”气动人工肌肉通常由约束层（包括约束线^[20]和约束布^[21]）和伸长型驱动器组成。约束层呈菱形布置，可将伸长型驱动器的伸长转化为整个气动人工肌肉的收缩，从而获得较高的收缩率和较大的收缩力。然而这类气动人工肌肉的尺寸很大、结构复杂、制造难度大，并且伸长型驱动器存在被压弯的风险。

随着新材料和新技术的发展，还出现了一种Peano电致伸缩驱动器^[22]。这种驱动器外形类似Peano气动人工肌肉，但是其2层可导电薄膜之间的空腔内部充满电介质液体，通过在薄膜上施加高压电来驱动肌肉收缩。该驱动器具有很快的响应速度，但是收缩率低且收缩力小。并且驱动电压极高，已接近材料的击穿电压，存在一定安全风险。

此外，以上气动人工肌肉大部分存在刚性零部件，这也限制了这类气动人工肌肉在可穿戴式设备上的应用。

为了解决上述问题，本文通过将平面收缩层、约束层和扁平气囊正交编织后形成了一种新型的扁平气动人工肌肉（以下简称扁肌）。此方法的优点在于只需要通过简单的制造和装配技术便可制造出性能优良的气动人工肌肉。整个扁肌无刚性零部件，具有良好的柔性和适应性。扁肌的收缩率也远高于传统的McKibben气动人工肌肉。并且由于扁肌自身重量非常轻，使得扁肌具有很大的驱动力重量比。更进一步地，扁肌的各主要部件均采用激光切割工艺制造，与传统的气动人工肌肉制造工艺相比，扁肌的制造工艺更加简单、制造效率更高。以上优点使得其具有广阔的应用前景。

2 结构设计（Structural design）

本文设计的扁肌的结构组成如图 1所示，主要由收缩层、约束层和扁平气囊组成。沿着扁肌收缩层上的长度方向切割有若干沟槽，因此在收缩层上形成了若干与沟槽等宽的细长收缩带，如图 1(a)所示。与此类似，约束层上同样设置有等宽的沟槽和约束带，如图 1(b)所示。约束带上等间距设置若干小孔，通过这些小孔，采用凯夫拉线将2个完全相同的约束层编织在一起，如图 1(c)所示。2层约束层编织的同时，将收缩层按照图 1(c)中的编织方法编入约束层中。编织完成后收缩层和约束层形成了一种双层扁平笼状结构。

由于气动人工肌肉的收缩率在一定程度上取决于气囊的膨胀率，为了增大充气前后气囊的厚度差，本设计采用无弹性的扁平气囊驱动扁肌收缩。扁平气囊具有多个气囊手指，如图 1(d)所示。在未充气状态下将2个扁平气囊的所有气囊手指插入扁平笼状结构中，形成完整的扁肌，如图 1(e)所示。

当扁平气囊充气后，气囊手指沿着其厚度方向膨胀，因此约束层的每根扁带呈S形交替包裹在气囊手指的外壁。在现有的编织工艺下，每个扁平气囊只受各自约束层的约束。同时，收缩层的所有收缩带均以S形交替包裹在所有气囊手指的外侧表面。由于约束层和收缩层拟采用高抗拉强度、低弯曲刚度的薄膜材料制造，可认为每根收缩带和约束带的长度保持不变。因此，扁平气囊膨胀后扁肌可沿着其长度方向收缩，但是其宽度方向的尺寸保持不变。

气囊手指的膨胀可引起约束层和收缩层的收缩。气囊手指膨胀迫使约束层弯曲变形，从而引起约束层产生直接收缩。另一方面，收缩层以S形绕在气囊手指外表面，从而导致收缩层在气囊手指表面产生较大滑移，外在效果表现为收缩层两端的距离显著减小，即扁肌产生显著收缩。

3 建模和仿真（Modeling and simulation） 3.1 扁肌收缩模型

采用图 1中的编织方式还可将扁肌扩展成由1层收缩层、$ n_{1} $层约束层和$ n_{1} $层扁平气囊编织而成的结构，其结构原理及变形后的结构如图 2(a)所示。因此，本小节将建立扁肌的通用收缩模型（扁平气囊和约束层的数量不限于2层）来描述其收缩性能。

由于扁肌的充气收缩过程较为复杂，为了简化分析，做出如下假设：1) 气囊手指膨胀后其外形轮廓为标准的圆弧形状；2) 忽略气囊手指和约束层、收缩层之间的摩擦；3) 忽略气囊材料、约束层和收缩层材料的拉伸变形；4) 扁肌收缩过程无能量损失；5) 忽略扁平气囊、约束层和收缩层的厚度。扁肌收缩后的总长度为$ X $，如图 2(a)所示。其中，单个气囊手指及其对应的部分约束层的变形如图 2(b)所示。由于约束层的原始节距$ L_{0} $（见图 1(b)）比气囊手指的原始宽度$ l_{0} $稍大，因此气囊手指充气变形后约束层并未与气囊手指完全贴合。根据假设，两者贴合的部分视为圆弧形（图 2(b)中的$ \overset\frown{AB} $），点$ A $和$ B $为圆弧的切点。约束层未与气囊手指贴合的部分仍然为直线形。因此，根据几何关系可得：

$ \begin{align} L&=\dfrac{2l_{0}} {\alpha} \left({\frac{1}{\sin \dfrac{\beta} {2}}-\cos \frac{\alpha} {2}\cot \frac{\beta} {2}} \right) \end{align} $

(1)

$ \begin{align} l&=\dfrac{2l_{0}} {\alpha} \sin \frac{\alpha}{2} \end{align} $

(2)

$ \begin{align} { h}&=\dfrac{2l_{0}} {\alpha} \left({1-\cos \frac{\alpha} {2}} \right) \end{align} $

(3)

其中$ L $为约束层收缩后的节距，$ \alpha $为气囊手指圆弧轮廓的圆心角，$ \beta $为$ \overset\frown{AB} $对应的圆心角，$ l $为气囊手指膨胀后的宽度，$ h $为气囊手指的膨胀高度。

$ \alpha $和$ \beta $满足下列几何关系：

$ \begin{align} \frac{1}{2} \left({L_{0} -\frac{l_{0}} {\alpha} \beta} \right)\sin \frac{\beta} {2}=\frac{l_{0}} {\alpha} \left({\cos \frac{\beta} {2}-\cos\frac{\alpha} {2}} \right) \end{align} $

(4)

因此，根据几何关系可计算整个扁平气囊的内腔体积$ V $和扁肌总厚度$ H $：

$ \begin{align} V&=n_{1} n_{2} bl_{0}^{2} \left({\frac{1}{\alpha} -\frac{\sin \alpha}{\alpha^{2}}} \right) \end{align} $

(5)

$ \begin{align} H&=n_{1} h \end{align} $

(6)

其中$ n_{1} $为扁平气囊的层数，$ n_{2} $为单个扁平气囊分割后气囊手指的数量，$ b $为气囊手指的长度。

整个扁肌收缩后的长度可表示为

$ \begin{align} X=&\{[{S_{0} \!-\!n_{2} l_{0} \!-\! ({n_{2} \!-\!1} )\sqrt{ ({n_{1} \!-\!1} )^{2}h^{2}\!+ \!({L{-l}} )^{2}}} ]^{2}\!- \\ &\!({n_{1} \!-\!1} )^{2}{h}^{2} \}^{-\frac{1}{2}}+({n_{2} -1} )L+l \end{align} $

(7)

其中$ S_{0} $为收缩层的原始长度。

因此扁肌的收缩率$ \varepsilon $可表示为

$ \begin{align} \varepsilon = \left({S_{0} -X} \right)/S_{0} \end{align} $

(8)

气动人工肌肉建模方法可分为受力分析法和虚功原理法，由于气动人工肌肉一般由软体材料构成，导致受力分析较为复杂，因此采用虚功原理对扁肌进行分析。在某一平衡状态下扁肌内部气压为$ P $，外力为$ F $，给扁肌一个虚位移d$ X $，根据虚功原理可得：

$ \begin{align} \left\{ \begin{aligned} {\rm d}W_{{\rm i}}& =P{\rm d}V \\ {\rm d}W_{{\rm o}}& =-F{\rm d}X \\ \end{aligned} \right. \end{align} $

(9)

其中$ {\rm d}W_{{\rm o}} $为输出功，$ {\rm d}W_{{\rm i}} $为输入功。

根据假设可知，扁肌工作过程中无能量损耗和存储，由能量守恒原理可得：

$ \begin{align} {\rm d}W_{{\rm o}} ={\rm d}W_{{\rm i}} \end{align} $

(10)

由式(9) 和式(10) 可得：

$ \begin{align} F=-P\frac{{\rm d}V \left(\alpha \right)}{{\rm d}X \left(\alpha \right)}=-P\frac{{\rm d}V/{\rm d}\alpha} {{\rm d}X/{\rm d}\alpha} \end{align} $

(11)

通过将式(1)~式(8) 代入式(11)，并消去$ \alpha $、$ \beta $等中间变量，理论上可以获得扁肌的收缩力与收缩率及气压之间的关系。由于公式比较复杂，无法直接通过化简得到收缩力的解析解。但是从上述公式的结构形式可以推测扁肌的收缩力方程在结构形式上可表示为

$ \begin{align} F=Pb\frac{l_{0}^{2}}{L_{0}} f \left(\varepsilon \right) \end{align} $

(12)

其中$ f \left(\varepsilon \right) $为与收缩率$ \varepsilon $有关的函数。

3.2 扁肌收缩仿真

为了模拟扁肌的结构特性和收缩特性，本文根据建立的理论模型进行了仿真分析，仿真使用的结构参数见表 1。

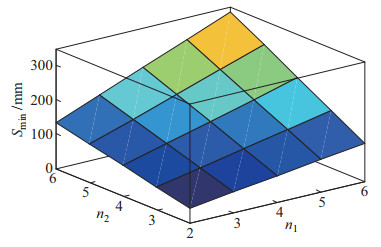
由扁肌的编织结构可知，当气囊手指的外形轮廓变为完整的圆形时（即$ \alpha = {\rm{ \mathsf{ π} }}$），扁肌的收缩率达到最大。但是气囊手指的膨胀受到收缩层的限制，当气囊手指宽度$ l_{0} $和约束层节距$ L_{0} $确定后，收缩层的长度$ S_{0} $存在最小值$ S_{\min} $，当$ S_{0}=S_{\min} $、$ \alpha = {\rm{ \mathsf{ π} }} $时，图 2中的$ \varphi = {\rm{ \mathsf{ π} }/2} $。根据几何关系可得$ S_{\min} $的解，见式(13)。$ S_{\min} $的仿真结果如图 3所示。从图中可知$ S_{\min} $随着$ n_{1} $和$ n_{2} $的增大而线性增大。当$ S_{0}>S_{\min} $后，继续增大$ S_{0} $会降低扁肌的收缩率（增大的收缩层长度不参与收缩），以下分析中各约束层长度$ S_{0} $均取该计算结果中的$ S_{\min} $。

$ \begin{align} S_{\min} &=\frac{2 \left({n_{2} -1} \right)l_{0}} {\rm{ \mathsf{ π}}} \sqrt{ \left({n_{1} -1} \right)^{2}+ \left(\sin^{-1}\frac{\beta} {2}-1 \right)^{2}}+\\[6pt] &\quad\; \left({\frac{2 \left({n_{1} -1} \right)}{\rm{ \mathsf{ π}}} +n_{2}} \right)l_{0} \end{align} $

(13)

其中$ \beta $满足关系：$ \tan \dfrac{\beta} {2}=\dfrac{2l_{0}} {{\mathsf{ π}} L_{0} -\beta l_{0}} $。

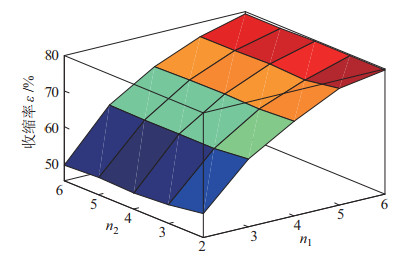
求解式(7) 和式(8) 可得不同结构扁肌的最大收缩率，如图 4所示。从计算结果可知，增大手指数量$ n_{2} $并不能增大扁肌的收缩率。而扁肌的最大收缩率随着扁平气囊层数$ n_{1} $逐渐增加。当扁平气囊层数为6时，扁肌的最大收缩率能达到80%，这远超过传统McKibben气动人工肌肉的收缩率。

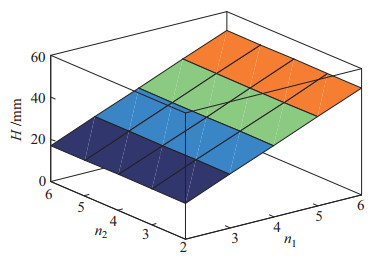
求解式(3) 和式(6) 可得扁肌收缩后的最大厚度$ H $，如图 5所示。从图 5中可知，气囊手指的数量$ n_{2} $对扁肌的厚度$ H $没有影响。扁肌的厚度$ H $会随着扁平气囊层数$ n_{1} $的增加而线性增大。当扁平气囊层数为6时，扁平气囊充气膨胀后，整个扁肌的最大厚度达到52 mm。由于扁肌厚度过大会使扁肌外形臃肿，影响扁肌的安装，因此实际应用中需要根据使用需求选择合适结构的扁肌。为了简化研究，本文将着重研究具有2层扁平气囊结构的扁肌。

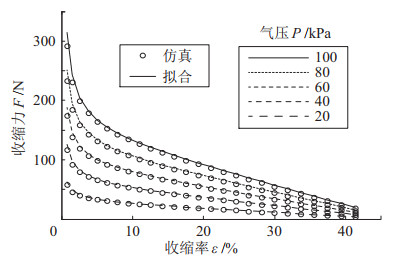
3.2节中建立的各方程较为复杂，很难获得扁肌的收缩力、收缩率及气压之间的显函数表达式。为了预测扁肌的收缩力特性，本文根据式(1)~式(12)，采用Matlab进行数值求解，获得了不同收缩率下扁肌的收缩力，仿真结果如图 6中的数据点所示。该仿真中扁平气囊层数为2，气囊手指数量为6，其余结构参数见表 1。从仿真结果可以看出，扁肌的收缩力曲线接近有理函数曲线，因此采用有理函数对仿真结果进行拟合，拟合曲线的表达式见式(14)。拟合曲线的系数见表 2。因此，拟合得到的式(14) 可作为扁肌收缩力的近似解析解。

$ \begin{align} F=Pb\frac{l_{0}^{2}}{L_{0}} {\frac{p_{1} \varepsilon ^{2}+p_{2} \varepsilon +p_{3}} {\varepsilon +q_{1}}} \end{align} $

(14)

4 样机研制与实验（Prototype development and experiments） 4.1 样机研制

为了保证收缩层和约束层的柔性和抗拉强度，本文采用0.15 mm厚的PET（涤纶树脂）膜来制造收缩层和约束层，并且两者均直接采用激光切割成型。PET膜具有很高的拉伸强度，从而保证扁肌能够承载较大的负载。

根据扁肌的工作特性可知，用于制造扁平气囊的材料需同时满足薄、密封性能好、低弹性、拉伸强度高、摩擦系数低等条件。相关文献采用了激光焊接工艺制造TPU（热塑性聚氨酯）气囊^[25]，但是由于薄膜TPU制作的气囊耐压有限，并且摩擦系数高，因此TPU气囊在此处并不适用。本文选用拉伸强度更高、表面摩擦系数更小的铝塑膜作为扁平气囊材料。铝塑膜由3层材料组成：PE（聚乙烯）内层、铝膜中间层、PET外层。PE内层能起到良好的密封作用，铝膜中间层赋予了整个膜较高的抗拉强度，外层PET材料增大了整个铝塑膜的耐磨特性，降低了摩擦系数。整个铝塑膜厚度仅0.09 mm。因此铝塑膜是制造扁平气囊的理想材料。

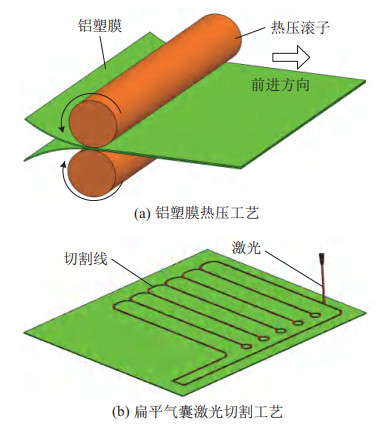
扁平气囊的制造工艺如图 7所示，主要分为2步：滚压和切割成型。如图 7(a)所示，将2层铝塑膜的PE内层相贴，采用热压的方式将2层膜临时压合在一起。本文选用的工艺参数为：加热温度为100$ {^\circ} $C，压膜的线速度为18 mm/s。在此工艺参数下压合的双层铝塑膜既能够比较好地贴合在一起，又能顺利地分开。如图 7(b)所示，采用激光切割工艺将双层铝塑膜切割成设计的形状，激光切割的切缝处2层膜的内层PE能够很好地融合粘接，起到密封和连接的作用。因此激光切割形状即为最终的扁平气囊成型形状。扁平气囊的激光切割工艺参数为：激光功率20%（CO$ _{2} $激光器额定功率130 W），切割速度50 mm/s，光斑尺寸1 mm。采用该工艺参数制作的扁平气囊耐压能力能达到300 kPa。

将PET收缩层、约束层与扁平气囊采用图 1中的编织方法编织成扁肌，如图 8(a)所示。该扁肌中扁平气囊层数为2，气囊手指数量为6，收缩层长度$ S_{0}= $ 136 mm，其余结构参数见表 1。整个扁肌质量仅有8.1 g，充气前的厚度仅有1.2 mm。从进气口向扁平气囊内部充入压缩空气后贴合在一起的2层铝塑膜分离，使得扁平气囊膨胀。扁平气囊膨胀会引起扁肌在长度方向产生收缩，如图 8(b)所示。

4.2 扁肌静态收缩实验

为了测试扁肌的收缩性能，本文搭建了实验平台进行了实验研究，如图 9所示。后续的动态收缩实验均在此平台上完成。用于实验的扁肌即为4.1节中制造的扁肌样机。

在扁肌静态收缩实验中，通过限位块限制扁肌的收缩率，采用高速比例阀（Festo VPPM-6L-L-1-G18-0L6H-V1N）控制扁肌的输入气压，通过拉力传感器（DYMH-103）测量不同气压下扁肌的收缩力，通过机架顶部的激光位移传感器（Keyence IL-1000）测量扁肌的收缩位移。扁肌的静态收缩实验结果如图 10中的数据点所示。使用最小二乘法，根据实验数据对上文建立的扁肌收缩力模型（见式(14)）中的参数进行辨识，获得的参数见表 3。根据辨识得到的参数计算得到扁肌的理论收缩特性数据，如图 10中的各曲线所示。从实验和计算结果可以看出，随着扁肌收缩率的增加，其收缩力逐渐减小，并且这种减缓趋势逐渐放缓。当收缩率超过15% 后，扁肌的收缩力基本上呈现线性减小的趋势，这更有利于后期研究中扁肌的控制。当收缩率为5%、驱动气压为200 kPa时，扁肌的收缩力达到280 N，是其自身重量的3 527倍，说明该扁肌具有极高的收缩力重量比。

由于本文在建模时作了相应的简化，而实际实验中气囊手指的轮廓形状与标准圆弧之间存在差异，摩擦和材料的弹性变形等因素也会对扁肌的收缩力产生影响。而不同气压下各因素的影响程度不同，因此模型参数便与气压产生了关联。为了建立模型参数与气压之间的关系，本文采用多项式拟合的方法获得各模型参数的表达式，见式(15)。结合式(14) 即可对各气压下的扁肌收缩性能进行预测，为后期研究扁肌的精密控制提供理论基础。

$ \begin{align} \begin{cases} p_{1} = \\ \dfrac{-3.01\times 10^{-5}P^{3}+0.01325P^{2}-4.334P+61.23}{P-7.599} \\[2pt] p_{2} = \\ \dfrac{1.896\times 10^{-5}P^{3}-0.007143P^{2}+1.941P-29.37}{P-6.07} \\[2pt] p_{3} = \\ \dfrac{-5.775\!\times\! 10^{-6}P^{3}\!+\!0.00192P^{2}\!-\!0.2251P\!+\!5.523}{P+23} \\[2pt] q_{1} = \\ \dfrac{- 4.808\!\times\! 10^{-6}P^{3} \!+ \!0.001578P^{2} \!- \!0.1919P \!+ \!3.395}{P+50.74} \\ \end{cases} \end{align} $

(15)

4.3 扁肌动态收缩实验

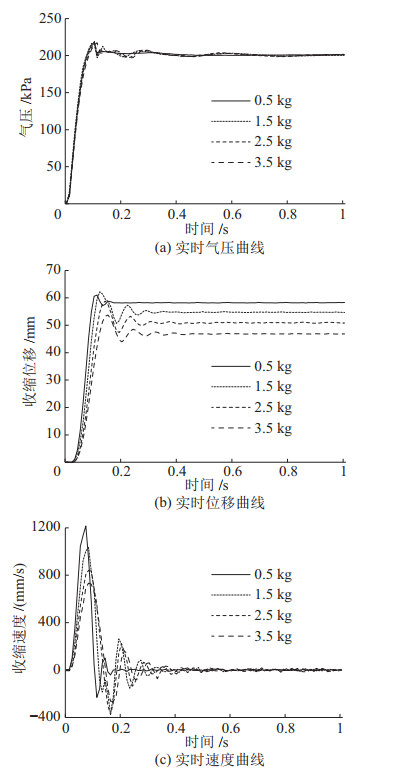
为了评价扁肌的动态收缩性能，首先进行扁肌对阶跃气压响应特性的测试。该实验中，在图 9中的滑块上加载恒定重量的负载，通过高速比例阀产生阶跃气压驱动扁肌收缩，高速比例阀内置的气压传感器可检测比例阀的实时输出气压（可近似认为扁肌内的气压与该气压相等）。本实验共测试了4种恒定负载下扁肌的阶跃响应特性。实验中所采用的阶跃气压为200 kPa，4种负载下扁肌的实时气压如图 11(a)所示。从11(a) 中可以看出，不同负载下扁肌均能在0.15 s内达到最大气压。这是因为在充气前扁肌中的扁平气囊的内腔体积接近0，从而使得扁肌具有较快的充气速度。不同负载下扁肌的实时气压变化特性基本相似，这是因为气压变化特性主要取决于比例阀的结构参数。

在上述阶跃气压的驱动下，扁肌的实时收缩位移和收缩速度如图 11(b)(c) 所示。与充气速度相对应，0.15 s内不同负载下的扁肌均能达到最大收缩位移，并且在0.5 s后扁肌的收缩位移基本稳定。随着负载的增大，扁肌的稳定收缩位移逐渐减小。当负载为0.5 kg时，扁肌的稳定收缩位移达到58.3 mm，对应的收缩率为42.8%。远大于传统的McKibben气动人工肌肉的最大收缩率（20% 左右）。从图 11(c)中的扁肌实时收缩速度可以看出，扁肌的收缩速度也随着负载的增大而降低。负载为0.5 kg时，扁肌的最大收缩速度达到1 216.2 mm/s。以上实验结果说明本文的扁肌兼具高收缩率和高收缩速度的特性。

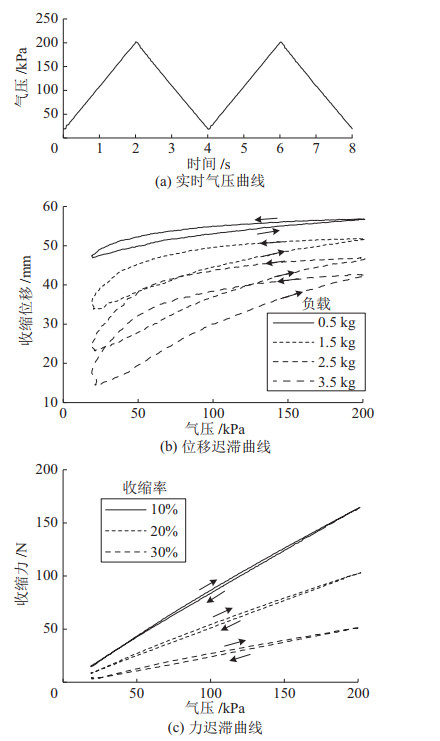
扁肌收缩时收缩层与扁平气囊之间存在较大滑移，由于两者之间存在摩擦，扁肌和其他气动人工肌肉一样存在迟滞现象。本文采用实验测量了扁肌的收缩位移迟滞和收缩力迟滞。在2项实验中，均采用如图 12(a)所示的按照三角波规律周期性变化的气压驱动扁肌收缩。并在扁肌上加载和阶跃实验中相同的4种重力负载，通过激光位移传感器测量扁肌的动态收缩位移，实验结果如图 12(b)所示。4种负载下扁肌的最大位移迟滞分别为2.4 mm、7.0 mm、10.0 mm和12.4 mm。扁肌的这种位移迟滞特性是由收缩层和扁平气囊之间的滑动摩擦造成的。扁肌收缩和伸长时的滑动摩擦力方向相反，因此负载越大，摩擦力越大，位移迟滞越严重。后期研究中将对扁肌的迟滞特性进行建模，从而使扁肌的收缩模型更加准确。

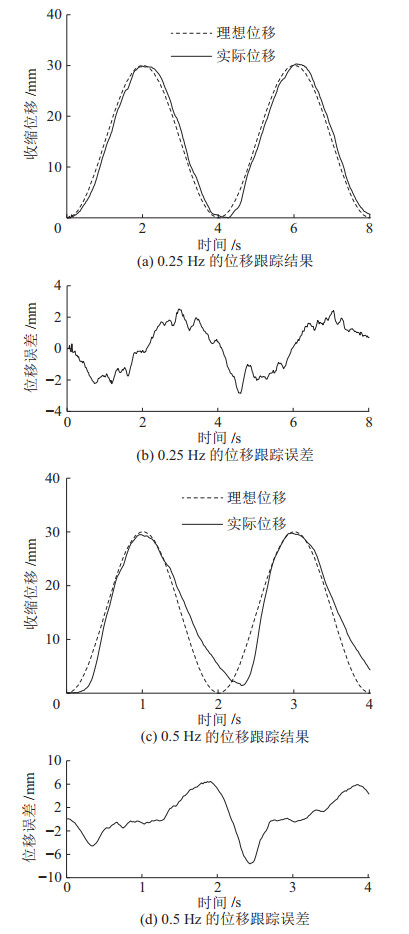
为了测试扁肌的位置跟踪性能，本文利用图 9中的实验平台进行了扁肌对正弦位置曲线的跟踪实验。实验中将激光位移传感器测量的扁肌实时收缩位移反馈给控制器，控制器采用PID控制算法控制比例阀对扁肌进行充放气，从而控制扁肌按照正弦规律进行收缩和伸长，实验结果如图 13(a)所示。从实验结果可以看出，扁肌对0.25 Hz的正弦曲线具有很好的跟踪效果。其误差曲线如图 13(b)所示，最大位移误差为2.5 mm，说明扁肌在该运动频率下位置跟踪精度较高。

从图 13(c)中的实验结果可以看出，扁肌以0.5 Hz的频率运动时存在一定延迟。尤其是在扁肌放气伸长阶段，其位移延迟更为严重。位移误差曲线如图 13(d)所示，最大位移误差6.5 mm。扁肌在该频率下运动存在较大位移误差的原因是：扁肌中的扁平气囊的材料不可拉伸，充气后气囊材料未储存弹性势能，从而造成其放气速度较慢，影响了扁肌的放气伸长速度。同时，由于扁肌存在固有的迟滞特性，造成扁肌在较高频率下的运动存在较大延迟。后期研究中可以通过拮抗布置扁肌来降低扁肌放气伸长的位置延迟误差。

5 结论（Conclusion）

本文提出了一种新型扁平气动人工肌肉的结构及其制造方法。采用正交编织工艺将约束层、收缩层与扁平气囊相互编织成一体形成整个扁肌，通过建模分析了扁肌的收缩层最小长度、扁肌的收缩率以及扁肌收缩后的最大厚度与扁平气囊的层数及气囊手指数量之间的关系，采用有理函数拟合法建立了扁肌收缩力的近似解析解，从而确定了实验所采用的扁肌的结构参数。通过简单的激光切割工艺切割出PET材料的约束层和收缩层，并结合热压工艺切割出铝塑膜材料的扁平气囊。编织完成的扁肌质量仅8.1 g，厚1.2 mm。

扁肌的收缩实验结果显示扁肌的最大收缩力达280 N，最大收缩率达42.8%。采用参数辨识方法对扁肌收缩力模型中的各模型参数进行了辨识，从而得到了扁肌收缩力的近似解析解。阶跃收缩实验表明扁肌具有良好的收缩性能以及快速响应性能。迟滞实验结果显示扁肌的力迟滞很小，不同负载下扁肌的力迟滞差异也并不明显。动态位置跟踪实验结果显示，扁肌对0.25 Hz的正弦信号具有良好的位置跟踪能力，最大位移误差为2.5 mm。

通过实验也暴露出扁肌存在的缺陷，如扁肌存在较大的位移迟滞，并且随着负载的增加，位移迟滞现象更加严重。在动态跟踪实验中，增大动态跟踪频率，扁肌也存在较大的位移延迟。针对存在的问题，未来将对扁肌的模型进一步优化，并加入迟滞现象对扁肌收缩位移的影响，实现位移迟滞的补偿。此外，通过结构优化提高扁平气囊的放气速度，从而提高扁肌的高频运动性能。进一步地，拟将扁肌实际应用于可穿戴式设备，并测试其使用性能，以便根据使用效果进一步优化扁肌结构。