空间机器人装有机械臂和末端执行器,可以完成空间救援、加油和飞船维修等复杂的空间任务。执行任务时,空间机器人需要具有自适应跟踪捕获目标的能力,而这种能力是空间操作的基础。当空间机器人开始捕获目标时,系统的喷气装置会关闭。在这种情况下,末端执行器的接近、跟踪运动将干扰不受控的基座[1]。此外,动力学方程的耦合、非线性和参数变化也会导致末端执行器跟踪精度变差,这严重影响了空间机器人的精细操作[2]。因此,在这些情况下,空间机器人实现末端执行器的高性能跟踪成为一个挑战性的课题。此外,空间机器人的机械臂能耗问题也被广泛关注。因此,在设计自适应跟踪控制器时,需要同时考虑以上这些问题。
空间机器人的控制具有2个难点。一个难点是空间机器人的动力学耦合问题。对于空间机器人动力学方程来说,飞行器和机械臂的运动既取决于动力学方程,也取决于运动学方程,这种互相关联、互相影响被称为动力学耦合[3]。这种动力学耦合将导致机械臂与飞行器的运动不协调。为了解决这种不协调问题,可采用卡尔曼滤波器去预测目标的运动状态,利用预测结果来规划机械臂的轨迹[4-5]。这种方法忽视了动力学建模,只规划末端执行器的运动轨迹。滑模控制和模型预测控制是处理耦合问题的常用方法,它们可以在一定程度上减少航天器姿态和机械臂运动之间的耦合带来的不利影响[6]。然而,这些方法都需要一个精确的、解耦的动力学模型。为了分析和量化动力学耦合程度,一些文献提出了动态耦合因子、耦合椭球面和可操作度等指标[7]。这些指标量化了动力学参数、连杆长度和关节变量对空间机器人耦合的影响,可用于机器人捕获目标的优化问题中。
另一个难点是空间机器人动力学模型的非线性。从动力学方程分析,这主要是关节力矩既存在于等号右边的输入项中,又存在于等号左边的偏置力项中,导致其无法成为独立项。对此,文[8]提出一种自适应变结构控制器来处理模型的这些非线性参数,但这种控制策略会产生抖振效应。采用最小二乘法估计了动力学回归方程的系数矩阵,把动力学方程近似为一组物理参数的线性方程。然而,这种方法对于复杂构形或多关节机器人来说,很难实现,复杂度极高[9]。动力学方程线性化之所以重要,是因为它被用在状态方程中,包括扩展卡尔曼滤波器[5]或神经网络中的状态估计器[10]。然而,由于动力学方程的系数矩阵是时变的,状态估计器很难获得满意的精度,特别是在采样时间较长的情况下。以往大多数关于动力学非线性的研究都是基于运动学层面的控制,当考虑到电机扰动、关节摩擦的影响时,动力学的非线性将变得更强。为了解决这个问题,可采用自适应模糊系统将动力学方程非线性项近似为关节角、速度和力矩的函数。通过这种方式,也可以处理电机和关节的扰动[11]。不幸的是,这种基于自适应模糊系统的控制器输出的转矩依然会导致抖振现象。这种抖振问题可以通过在切换表面周围引入边界层来缓解,但跟踪性能会恶化[12]。还有方法将模型参数化为机械臂质量、惯量和长度的函数,但该方法存在严重的不确定性,无法应用于复杂条件和多关节机器人[13]。
动力学不确定性也可能严重破坏基于模型的控制方案的跟踪精度,甚至导致闭环机器人系统的不稳定行为[14]。这种不确定性的原因是多方面的,包括优化误差、测量误差带来的不确定性,此外还有外界未知扰动、本体参数变化等不确定性。总的来说,在动力学方程的线性化方面,以往的研究大多倾向于采用智能算法对一些关键参数进行学习、拟合和近似,或者研究可以直接导出符号公式的简单构形机器人。为了避免动力学方程的复杂推导,一些研究人员基于动量守恒和速度雅可比矩阵[15-20]来研究动力学。这些方法难以应用于空间机器人和复杂构形机器人。许多研究者同样认为动力学模型的线性化和解耦对于现代控制理论是至关重要的[9]。然而,关于空间机器人的显式线性解耦方程的研究成果却较少。
空间机器人控制策略除了考虑非线性、耦合和不确定性对跟踪精度造成的影响外,还需要同时考虑机械手的能耗问题。在太空中,航天器推进器储备的能量是有限的。驱动机械臂运动是需要消耗能量的。通过比较几种控制方法的能耗,得出飘浮飞行器比受控飞行器能耗低的结论[21]。文[22]对机械臂的能耗优化进行了研究和分析。遗憾的是,在能源消耗方面,这只是基于最优积分滑模控制的一种改进方法,较少的能源消耗只是一个附属结论。此外,一些研究将机械臂能耗表述为约束最优控制问题,利用逆雅可比矩阵离线粗略计算输入关节力矩[23-24]。这种离线粗略估计,会给系统带来不确定性和奇异性,导致跟踪误差较大。
针对上述问题,本文提出一种空间机器人自适应跟踪控制策略。该方法将空间机器人跟踪动力学方程线性化并解耦为显式方程,提高了控制方法的效率和精度。该控制器避免了加速度规划和速度测量,直接计算末端执行器的未来速度,具有工程意义。本文除了考虑控制器的跟踪精度外,还考虑了控制器的能耗。因此,还研究了自适应跟踪控制器设计中的能量效率问题。本文的主要贡献如下:
1) 将系统动力学线性化并解耦,得到显式状态方程。状态方程将关节力矩从动力学中解耦,并描述了力矩与末端执行器速度之间的线性相关关系。
2) 在耦合、非线性、不确定性和任务约束条件下,提出了一种自适应跟踪控制策略。该方法可以实现避碰,避免了对目标加速度和速度的测量,对实际工程项目具有一定的指导意义。用李雅普诺夫函数证明了该控制策略的收敛性。
3) 将空间机器人的能耗问题视为一个约束最优控制问题,提出了一种具有相同跟踪性能但能耗较少的最优控制器。
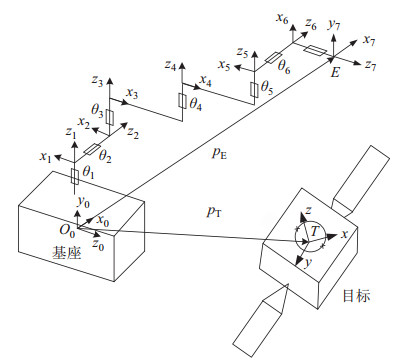
2 运动学与动力学模型(Kinematic and dynamic models)目前,大部分空间机器人都装有简单构形的机械臂,如平面机械臂和少关节机械臂。对于这些机械臂,很容易建立数学模型并进行验证。对于复杂构形操作机,一般会采用迭代法推导出耦合和非线性的动力学模型。为了避免推导动力学模型,许多研究人员基于动量守恒和速度雅可比矩阵等方法推导了动力学模型,但误差的不确定性将导致控制器不准确。本文对动力学方程中包含的所有力矩项求导,然后将关节力矩解耦为独立项,并从动态方程中解耦出来,得到了末端执行器速度与关节力矩之间的动力学线性方程。
2.1 运动学本文将研究一个具有7关节机械臂的空间机器人。飞行器基座、机械臂各主体和末端执行器依次连接。基座编号0,机械臂机构编号从1到

|
图 1 空间机器人的几何模型 Fig.1 The geometric model of the space robot |
这里采用一种紧凑的符号来研究刚体运动学:
| $ \begin{align} {\mathit{\boldsymbol{v}}} = \left[ {\begin{array}{*{20}{c}} \underline{\mathit{\boldsymbol{\omega}}}\\ \underline{\mathit{\boldsymbol{v}}} \end{array}} \right], \; \; \; {\mathit{\boldsymbol{f}}} = \left[ {\begin{array}{*{20}{c}} \underline{\mathit{\boldsymbol{n}}}\\ \underline{\mathit{\boldsymbol{f}}} \end{array}} \right], \; \; \; {\mathit{\boldsymbol{a}}} = \left[ {\begin{array}{*{20}{c}} \underline{\dot{\mathit{\boldsymbol{\omega}}}}\\ \underline{\dot{\mathit{\boldsymbol{v}}}} - \underline{\mathit{\boldsymbol{\omega}}} \underline{\times} \underline{\mathit{\boldsymbol{v}}} \end{array}} \right] \in \mathbb{R}^{6 \times 1} \end{align} $ | (1) |
其中
本文采用铰接体算法[25]推导了空间机器人的动力学方程。这种方程可以保持欧拉方程形式:
| $ \begin{align} {\mathit{\boldsymbol{f}}_i} = {\mathit{\boldsymbol{I}}}_i^{\rm A}{{\mathit{\boldsymbol{a}}}_i} + \mathit{\boldsymbol{p}}_i^{\rm A} \end{align} $ | (2) |
其中
| $ \begin{align*} {\mathit{\boldsymbol{I}}}_{i}^{\rm A} =\;& {\mathit{\boldsymbol{I}}}_{i} +{}^{i}{\mathit{\boldsymbol{X}}}_{c(i)}^{*} ({{\mathit{\boldsymbol{I}}}_{c(i)}^{\rm A} -{\mathit{\boldsymbol{I}}}_{c(i)}^{\rm A} {\mathit{\boldsymbol{S}}}_{c(i)}} ({{\mathit{\boldsymbol{S}}}_{c(i)}^{\rm T} {\mathit{\boldsymbol{I}}}_{c(i)}^{\rm A} {\mathit{\boldsymbol{S}}}_{c(i)}})^{-1}\times \\ & {\mathit{\boldsymbol{S}}}_{c(i)}^{\rm T} {\mathit{\boldsymbol{I}}}_{c(i)}^{\rm A})^{c(i)}{\mathit{\boldsymbol{X}}}_{i} \\ {\mathit{\boldsymbol{p}}}_{i}^{\rm A} =\;& {\mathit{\boldsymbol{p}}}_{i} +{}^{i}{\mathit{\boldsymbol{X}}}_{c(i)}^{*} ({{\mathit{\boldsymbol{p}}}_{c(i)}^{\rm a} +{\mathit{\boldsymbol{I}}}_{c(i)}^{\rm A} {\mathit{\boldsymbol{S}}}_{c(i)}} ({{\mathit{\boldsymbol{S}}}_{c(i)}^{\rm T} {\mathit{\boldsymbol{I}}}_{c(i)}^{\rm A} {\mathit{\boldsymbol{S}}}_{c(i)}})^{-1} \times\\ & ({\tau_{i} -{\mathit{\boldsymbol{S}}}_{c(i)}^{\rm T} {\mathit{\boldsymbol{p}}}_{c(i)}^{\rm A}})) \\ {\mathit{\boldsymbol{p}}}_{i} =\;& {\mathit{\boldsymbol{v}}}_{i} \times^{*} {\mathit{\boldsymbol{I}}}_{i} {\mathit{\boldsymbol{v}}}_{i} \end{align*} $ |
| $ \begin{align} \tau _i = {\mathit{\boldsymbol{S}}}_i^{\rm T} {\mathit{\boldsymbol{f}}_i} \end{align} $ | (3) |
| $ \begin{align} \ddot{\mathit{\boldsymbol{\theta}}}= \mathit{\boldsymbol{M}}_{\tau} {\mathit{\boldsymbol{\tau}}} + ({\mathit{\boldsymbol{U}}_0} - {\mathit{\boldsymbol{M}}^{- 1}}\mathit{\boldsymbol{C}}\dot {\bm\theta}) \end{align} $ | (4) |
由式(2)(3) 可知,
| $ \begin{align} \frac{\partial {\ddot{\theta}}}{\partial {\mathit{\boldsymbol{\tau}}}}= \frac{\partial} {{\partial {\mathit{\boldsymbol{\tau}}}}}{\mathit{\boldsymbol{M}}^{- 1}}({{\mathit{\boldsymbol{\tau}}} - {\mathit{\boldsymbol{U}}_{\rm g}} - \mathit{\boldsymbol{C}}\dot{\bm\theta}}) \end{align} $ | (5) |
将式(4) 代入式(5) 可得
| $ \begin{align} \frac{{\partial {\mathit{\boldsymbol{M}}^{- 1}}}}{{\partial {\mathit{\boldsymbol{\tau}}}}}= {\mathit{\boldsymbol{0}}}, \quad \frac{\partial} {{\partial {\mathit{\boldsymbol{\tau}}}}}({{\mathit{\boldsymbol{C\dot \theta}}}})= {\mathit{\boldsymbol{0}}}, \quad \frac{{\partial {\mathit{\boldsymbol{\tau}}}}}{{\partial {\mathit{\boldsymbol{\tau}}}}}= {\mathit{\boldsymbol{E}}} \end{align} $ | (6) |
和
| $ \begin{align} \frac{{\partial {\mathit{\boldsymbol{U}}_{\rm g}}}}{{\partial {\mathit{\boldsymbol{\tau}}}}}= {\mathit{\boldsymbol{I}}}_0^{\rm J}{({{\mathit{\boldsymbol{I}}}_0^{\rm A}})^{- 1}}\frac{{\partial \mathit{\boldsymbol{p}}_0^{\rm A}}}{{\partial {\mathit{\boldsymbol{\tau}}}}} + \frac{\partial} {{\partial {\mathit{\boldsymbol{\tau}}}}} [{\mathit{\boldsymbol{p}}_1^{\rm A} \cdots \mathit{\boldsymbol{p}}_N^{\rm A}}]^{\rm T} {{\mathit{\boldsymbol{S}}}_i} \end{align} $ | (7) |
其中
| $ \begin{align} \frac{{\partial \mathit{\boldsymbol{p}}_{p(i)}^{\rm A}}}{{\partial {\mathit{\boldsymbol{\tau}}}}}= {\mathit{\boldsymbol{F}}}_i^\tau + {\mathit{\boldsymbol{F}}}_i^{\mathit{\boldsymbol{p}}}\frac{{\partial \mathit{\boldsymbol{p}}_i^{\rm A}}}{{\partial {\mathit{\boldsymbol{\tau}}}}} \end{align} $ | (8) |
其中,
| $ \begin{align} & \frac{{\partial \mathit{\boldsymbol{p}}_0^{\rm A}}}{\partial {\mathit{\boldsymbol{\tau}}}}= \left[{\mathit{\boldsymbol{F}}}_1^{\mathit{\boldsymbol{\tau}}}, {\mathit{\boldsymbol{F}}}_1^{\mathit{\boldsymbol{p}}}{\mathit{\boldsymbol{F}}}_2^{\mathit{\boldsymbol{\tau}}}, {\mathit{\boldsymbol{F}}}_1^{\mathit{\boldsymbol{p}}}{\mathit{\boldsymbol{F}}}_2^{\mathit{\boldsymbol{p}}}{\mathit{\boldsymbol{F}}}_3^{\mathit{\boldsymbol{\tau}}}, \cdots, \left({ \prod _{i = 1}^{N - 1} {\mathit{\boldsymbol{F}}}_i^{\mathit{\boldsymbol{p}}}}\right) \mathit{\boldsymbol{F}}_N^{\mathit{\boldsymbol{\tau}}} \right] \end{align} $ | (9a) |
| $ \begin{align} & {\mathit{\boldsymbol{S}}}_F \triangleq \frac{\partial} {{\partial {\mathit{\boldsymbol{\tau}}}}}{[{\mathit{\boldsymbol{p}}_1^{\rm A} \cdots \mathit{\boldsymbol{p}}_N^{\rm A}}]^{\rm T}}{{\mathit{\boldsymbol{S}}}_i} \\ &= \left[ {\begin{array}{*{20}{c}} 0 & {{\mathit{\boldsymbol{S}}}_2^{\rm T}{\mathit{\boldsymbol{F}}}_2^{\mathit{\boldsymbol{\tau}}}} & {{\mathit{\boldsymbol{S}}}_2^{\rm T}{\mathit{\boldsymbol{F}}}_2^{\mathit{\boldsymbol{p}}}{\mathit{\boldsymbol{F}}}_3^{\mathit{\boldsymbol{\tau}}} \cdots} & {{\mathit{\boldsymbol{S}}}_2^{\rm T} \left({ \prod \limits_{i = 2}^{N - 1} {\mathit{\boldsymbol{F}}}_i^{\mathit{\boldsymbol{p}}}}\right) {\mathit{\boldsymbol{F}}}_N^{\mathit{\boldsymbol{\tau}}}}\\ 0 & 0 & {{\mathit{\boldsymbol{S}}}_3^{\rm T}{\mathit{\boldsymbol{F}}}_3^{\mathit{\boldsymbol{\tau}}} \cdots} & {{\mathit{\boldsymbol{S}}}_3^{\rm T} \left({ \prod \limits_{i = 3}^{N - 1} {\mathit{\boldsymbol{F}}}_i^{\mathit{\boldsymbol{p}}}}\right) {\mathit{\boldsymbol{F}}}_N^{\mathit{\boldsymbol{\tau}}}}\\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {\mathit{\boldsymbol{S}}_N^{\rm T}{\mathit{\boldsymbol{F}}}_N^{\mathit{\boldsymbol{\tau}}}}\\ 0 & 0 & \cdots & 0 \end{array}} \right] \end{align} $ | (9b) |
式(9b) 中
| $ \begin{align} {\mathit{\boldsymbol{M}}_{\mathit{\boldsymbol{\tau}}}}= {\mathit{\boldsymbol{M}}^{- 1}} - {\mathit{\boldsymbol{M}}^{- 1}}{\mathit{\boldsymbol{M}}_0} \end{align} $ | (10) |
其中
| $ \begin{align} {\mathit{\boldsymbol{U}}_0}= {\mathit{\boldsymbol{M}}^{- 1}}{\mathit{\boldsymbol{M}}_0}{\mathit{\boldsymbol{\tau}}} - {\mathit{\boldsymbol{M}}^{- 1}}{\mathit{\boldsymbol{U}}_{\rm g}} \end{align} $ | (11) |
上式中与
| $ \begin{align} {\mathit{\boldsymbol{\tau}}}= \mathit{\boldsymbol{M}}_{\tau}^{- 1}({{\ddot{\theta}} - {\mathit{\boldsymbol{U}}_0} + {\mathit{\boldsymbol{M}}^{- 1}} \mathit{\boldsymbol{C}}\dot{\theta}}) \end{align} $ | (12) |
这样,力矩就从动力学方程解耦,并得到关节加速度和力矩的线性方程。采用线性时变系统状态方程离散化方法,得到一个动态的离散状态方程。离散时间状态方程采用系统输入和输出信号的当前和过去值来更新状态。离散时间状态方程可离散为
| $ \begin{align} \dot{\mathit{\boldsymbol{\theta}}}_{k + 1} = {\mathit{\boldsymbol{A}}}{{\dot{\theta}}_k} + {\mathit{\boldsymbol{B}}}{\mathit{\boldsymbol{\tau}}_k} + {\mathit{\boldsymbol{w}}} \end{align} $ | (13) |
其中
| $ \begin{align} \ddot{\mathit{\boldsymbol{\theta}}}_k\delta t = \dot{\mathit{\boldsymbol{\theta}}}_{k+1}-\dot{\mathit{\boldsymbol{\theta}}}_k \end{align} $ | (14) |
动力学离散状态方程直接给出了关节扭矩和关节速度之间的关系。
控制器的目的是驱动末端执行器从初始构形开始执行期望的轨迹。基于速度的控制方案在协调操作[23]、避碰[24]、预测控制[9]和轨迹规划[25]中得到了广泛的应用。如图 2所示,本文研究的空间机器人系统由自由飘浮飞行器基座与SSRMS型机械臂组成。文中假设基座和机械臂都是刚体。
|
图 2 自由飘浮空间机器人捕获目标的原理图 Fig.2 Schematic of the free-floating space robot capturing a target |
在操作场景中,目标在惯性空间中不受外力并已失效。末端执行器坐标系
| $ \begin{align} {\mathit{\boldsymbol{p}}_E}({{t_{\rm f}}})= {\mathit{\boldsymbol{p}}_T}({{t_{\rm f}}}) \end{align} $ | (15) |
假设由耦合扰动引起的基座飘移不会使捕获点逃离机械手工作空间。位姿误差为
| $ \begin{align} {\mathit{\boldsymbol{e}}} = {\mathit{\boldsymbol{p}}_T} - {\mathit{\boldsymbol{p}}_E} \end{align} $ | (16) |
其中
| $ \begin{align} {\mathit{\boldsymbol{v}}_{\rm d}}= [ \dot{\underline{\mathit{\boldsymbol{\varPsi}}}}_{\rm d}, \underline{\mathit{\boldsymbol{v}}}_{\rm d}]^{\rm T} = \mathit{\boldsymbol{v}}_{\rm e} + {\hat{{\mathit{\boldsymbol{v}}}}}_T \end{align} $ | (17) |
其中
| $ \begin{align} \mathit{\boldsymbol{v}}_{\rm e} = k(t){\mathit{\boldsymbol{e}}} \end{align} $ | (18) |
估计速度的自适应速率为
| $ \begin{align} \dot{\hat{{\mathit{\boldsymbol{v}}}}}_T = {\mathit{\boldsymbol{K}}_{\rm e}} {\mathit{\boldsymbol{e}}} + {\mathit{\boldsymbol{K}}_{\rm B}} {\tilde{\mathit{\boldsymbol{v}}}_T} \end{align} $ | (19) |
其中
| $ \begin{align} {{\tilde{{\mathit{\boldsymbol{v}}}}}_T}= {\mathit{\boldsymbol{v}}_T} - {\hat{{\mathit{\boldsymbol{v}}}}}_T \end{align} $ | (20) |
关节限速
| $ \begin{align} k(t) = \begin{cases} \dfrac{{| {{\mathit{\boldsymbol{v}}_{\rm{elim}}}} |}}{{| {\mathit{\boldsymbol{e}}} |}}, & \dfrac{| {{\mathit{\boldsymbol{v}}_{\rm{elim}}}} |}{| {\mathit{\boldsymbol{e}}} |} < k_0\\ k_0, & \dfrac{{| {{\mathit{\boldsymbol{v}}_{\rm{elim}}}} |}}{{| {\mathit{\boldsymbol{e}}} |}} \geqslant k_0 \end{cases} \end{align} $ | (21) |
其中
| $ \begin{align} {{\hat{{\mathit{\boldsymbol{v}}}}}_T} = \int_0^{t} {\mathit{\boldsymbol{K}}_{\rm e}} {\mathit{\boldsymbol{e}}}{\rm d}t + {\mathit{\boldsymbol{K}}_{\rm B}} \left({{\mathit{\boldsymbol{p}}_T} - {\mathit{\boldsymbol{p}}_{T0}} - \int_0^{t} \hat{{\mathit{\boldsymbol{v}}}}_T {\rm d}t}\right) \end{align} $ | (22) |
其中
| $ \begin{align} & \min \limits_{\mathit{\boldsymbol{\tau}}} \; {\mathit{\boldsymbol{\varGamma}}}({{{\left\| {{\varGamma_{{\rm v}}} ({{\mathit{\boldsymbol{v}}_E} - {\mathit{\boldsymbol{v}}_{\rm d}}})} \right\|}^2} + {{\left\| {{\varGamma _{\rm p}}{\dot{\theta} \bm\tau}} \right\|}^2}}) \\ & {\rm{s.t.}}\; {\mathit{\boldsymbol{v}}_E}({{t_{{\rm f}}}})= {\mathit{\boldsymbol{v}}_{T}}({{t_{{\rm f}}}}), \quad {\mathit{\boldsymbol{v}}_E}({{t_0}}) = 0 \\ & \phantom{{\rm{s.t.}}\; }\mathit{\boldsymbol{p}}_E ({{t_{{\rm f}}}})= {\mathit{\boldsymbol{p}}_{T}}({{t_{{\rm f}}}}), \quad {\mathit{\boldsymbol{p}}_E}({{t_0}})= {\mathit{\boldsymbol{p}}_{E0}} \end{align} $ | (23) |
其中
| $ \begin{align} \rho = \mathit{\boldsymbol{\varPsi}}_{\tau}^{\rm T} \bm\tau + {\mathit{\boldsymbol{b}}} \end{align} $ | (24) |
其中
| $ \begin{align*} {\mathit{\boldsymbol{\varPsi}}}_{\tau} =\left[ {\begin{array}{*{20}{c}} {-\varGamma_{\rm v} {\mathit{\boldsymbol{S}}}_{\rm 0J} {\mathit{\boldsymbol{B}}}} \\ {\varGamma_{\rm p} \dot{\mathit{\boldsymbol{\theta}}}} \end{array}} \right], \quad {\mathit{\boldsymbol{b}}} =\left[ {\begin{array}{*{20}{c}} {\varGamma_{\rm v} ({{\mathit{\boldsymbol{v}}}_{E} -{\mathit{\boldsymbol{S}}}_{\rm 0J} \mathit{\boldsymbol{A\dot{\theta}}}-{\mathit{\boldsymbol{S}}}_{\rm 0J} {\mathit{\boldsymbol{w}}}})} \\ 0 \end{array}} \right] \end{align*} $ |
那么,优化目标函数可以表达成
| $ \begin{align} \min\limits_{\mathit{\boldsymbol{\tau}}} {\mathit{\boldsymbol{\varGamma}}}= \min \limits_{\mathit{\boldsymbol{\tau}}} {\rho^{\rm T}} \rho \end{align} $ | (25) |
式(25) 的极值条件是
| $ \begin{align} \frac{{{\rm d}{\rho^{\rm T}} \rho}}{{{\rm d}{\mathit{\boldsymbol{\tau}}}}}{\rm{= 2}}\frac{{{\rm d}{\rho^{\rm T}}}}{{{\rm d}{\mathit{\boldsymbol{\tau}}}}}\rho = 2\mathit{\boldsymbol{\varPsi}}_{\tau}^{\rm T} \rho = 0 \end{align} $ | (26) |
在初始条件约束下,可以得到式(23) 的最优控制力矩
| $ \begin{align} {\mathit{\boldsymbol{\tau}}}= ({\mathit{\boldsymbol{\varPsi}}_{\tau}^{\rm T} {\mathit{\boldsymbol{\varPsi}}_{\tau}}})^{- 1} \mathit{\boldsymbol{\varPsi}}_{\tau}^{\rm T} {\mathit{\boldsymbol{b}}} \end{align} $ | (27) |
控制器不仅需要跟踪期望轨迹,还需要满足避障、关节限制等一系列约束条件,同时优化误差和速度不可测带来的不确定性,也会影响控制器精度。因此在考虑以上约束与补偿后,控制模型变成了非线性、非凸的优化问题。
3.2 不确定性真实的在轨任务中,通过视觉传感器精确测量抓捕点速度
| $ \begin{align} | {{\mathit{\boldsymbol{v}}_T}} | \leqslant {\rho_{\rm a1}} , \quad | {{{{\dot{{\mathit{\boldsymbol{v}}}}}}_T}} | \leqslant {\rho_{\rm a2}} \end{align} $ | (28) |
其中
| $ \begin{align} | {{\mathit{\boldsymbol{\varDelta}}_{\rm p}}} |= | {{\mathit{\boldsymbol{v}}_E} - {\mathit{\boldsymbol{v}}_{\rm d}}} | \leqslant {\rho _{\rm p}} \end{align} $ | (29) |
| $ \begin{align} {\mathit{\boldsymbol{v}}_E}= {\mathit{\boldsymbol{v}}_{\rm d}} + {\mathit{\boldsymbol{\varDelta}}_{\rm p}} \end{align} $ | (30) |
| $ \begin{align} {\mathit{\boldsymbol{v}}_{\rm d}} = {\mathit{\boldsymbol{v}}_{\rm e}} + {{\hat{{\mathit{\boldsymbol{v}}}}}_T} - \int_0^{t} {\rm{sgn}} \overset\frown{\boldsymbol{v}} _{T} \left({{\rho_{\rm a}} + \frac{{2{\rho_{\rm p}}}}{{\delta t}}}\right){\rm d}t \end{align} $ | (31) |
其中
| $ \begin{align} {{\tilde{{\mathit{\boldsymbol{v}}}}}_T}= {\mathit{\boldsymbol{v}}_T} - \overset\frown{\boldsymbol{v}} _{T} \end{align} $ | (32) |
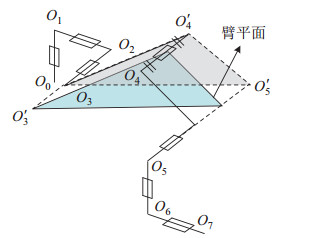
图 2中展示了SSRMS机械臂,不难发现碰撞总是发生在肘关节
| $ \begin{align} \varepsilon ^3 ({{\mathit{\boldsymbol{p}}}^{{\rm b}}}, \bm\varUpsilon) \end{align} $ | (33) |
其中
| $ \begin{align} {\mathit{\boldsymbol{d}}}({\bm\theta (\varphi)}) \geqslant {\mathit{\boldsymbol{d}}_{\rm s}}, \quad {\dot{{\mathit{\boldsymbol{d}}}}}({\dot {\bm\theta} (\varphi)}) \leqslant {\overline{\mathit{\boldsymbol{d}}}_{\rm s}} \end{align} $ | (34) |
|
图 3 避碰中机械臂简化模型与臂平面 Fig.3 The arm plane and the simplified manipulator model in collision avoidance |
|
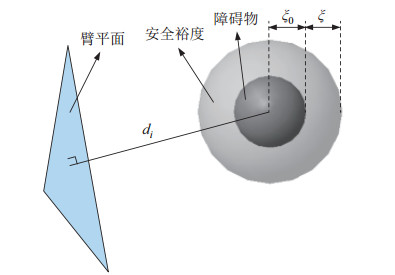
图 4 机械臂避障模型 Fig.4 Obstacle avoidance model of the manipulator |
关节不仅有角度和速度限制,而且有扭矩限制。机械臂关节需要满足
| $ \begin{gather} \underline{\mathit{\boldsymbol{\tau}}} \leqslant {\mathit{\boldsymbol{\tau}}} \leqslant {\overline{\tau}} \end{gather} $ | (35) |
| $ \begin{gather} \underline{\mathit{\boldsymbol{\theta}}} \leqslant \bm\theta (\varphi) \leqslant \overline{\theta}, \quad \underline{\dot{\theta}} \leqslant \dot{\theta} (\varphi) \leqslant \overline{\dot{\bm\theta}} \end{gather} $ | (36) |
综上所述,空间机器人跟踪目标的最优控制问题可以表述为带有线性等式和不等式约束的二次规划问题,其在
| $ \begin{align} & \min \limits_{{\mathit{\boldsymbol{\tau}}_k}} {\mathit{\boldsymbol{\varGamma}}} \left({{{\left\| {{\varGamma_{{\rm v}}} ({{\mathit{\boldsymbol{v}}_{Ek}} - {\mathit{\boldsymbol{v}}_{{{\rm d}} k}}})} \right\|}^2} + {{\left\| {{\varGamma_{\rm p}} {{{\dot{\theta}}}_k}{\mathit{\boldsymbol{\tau}}_k}} \right\|}^2}}\right) \\ & {\rm{s.t. }} {\mathit{\boldsymbol{v}}_{{{\rm d}} k}}= {\mathit{\boldsymbol{v}}_{{\rm e} k}} + {\hat{{\mathit{\boldsymbol{v}}}}_{Tk}} - \sum\limits_{i = 0}^k {\rm{sgn}} \overset\frown{\boldsymbol{v}} _{Tk} \left({{\rho_{\rm a}} + \frac{{2{\rho_{\rm p}}}}{{\delta t}}}\right) \delta t \\ & \phantom{{\rm{s.t. }}} {\mathit{\boldsymbol{v}}_E}({{k_{{\rm f}}}})= {\mathit{\boldsymbol{v}}_T}({{k_{{\rm f}}}}), \; \; {\mathit{\boldsymbol{v}}_E}(0)= 0 \\ & \phantom{{\rm{s.t. }}} {\mathit{\boldsymbol{p}}_E}({{k_{{\rm f}}}})= {\mathit{\boldsymbol{p}}_T}({{k_{{\rm f}}}}), \; \; {\mathit{\boldsymbol{p}}_E}(0)= {\mathit{\boldsymbol{p}}_{E0}} \\ & \phantom{{\rm{s.t. }}} {\mathit{\boldsymbol{d}}}({\bm\theta ({{\varphi _k}})}) \geqslant {\mathit{\boldsymbol{d}}_{\rm s}}, \; \; {\dot{{\mathit{\boldsymbol{d}}}}}({\dot {\bm\theta} ({{\varphi _k}})}) \leqslant {{{\overline{{\mathit{\boldsymbol{d}}}}}}_{\rm s}} \\ & \phantom{{\rm{s.t. }}} \underline{\theta} \leqslant \mathit{\boldsymbol{\theta}}_k \leqslant \overline{\theta}, \; \; \dot{\underline{\theta}} \leqslant {{\dot {\bm\theta}} _k} \leqslant \overline{\dot{\theta}} \\ & \phantom{{\rm{s.t. }}} | {{\mathit{\boldsymbol{v}}_{Ek}} - {\mathit{\boldsymbol{v}}_{{\rm d} k}}} | \leqslant {\rho _\rho} \\ & \phantom{{\rm{s.t. }}} \underline{\mathit{\boldsymbol{\tau}}} \leqslant \mathit{\boldsymbol{\tau}}_k \leqslant \overline{\tau} \end{align} $ | (37) |
序列凸规划法在对式(37) 最优控制的解算中取得了一定的成功。但是,这种方法每次迭代都要计算代价函数,在复杂约束条件下寻求最优解,计算效率较低。为了克服这一点,本文提出一种新的分段优化方法。
第1阶段优化主要是对运动学进行优化,实现避障、关节运动限制和末端执行器速度要求,其分别对应式(34)(36)(30)。这部分优化可以得到一些中间变量,例如
| $ \begin{align} & \min \limits_{{\mathit{\boldsymbol{\tau}}_k}} {\mathit{\boldsymbol{\varGamma}}}({{{\left\| {{\varGamma_{{\rm v}}} ({{\mathit{\boldsymbol{v}}_{Ek}} - {\mathit{\boldsymbol{v}}_{{{\rm d}} k}}})} \right\|}_2} + {{\left\| {{\varGamma_{\rm p}} {{{\dot{\theta}}}_k}{\mathit{\boldsymbol{\tau}}_k}} \right\|}_2}}) \\ & {\rm{s.t. }}\; \underline{\tau} \leqslant {\mathit{\boldsymbol{\tau}}_k} \leqslant {\overline{\tau}} \end{align} $ | (38) |
这样只有当式(27) 中求得的
|
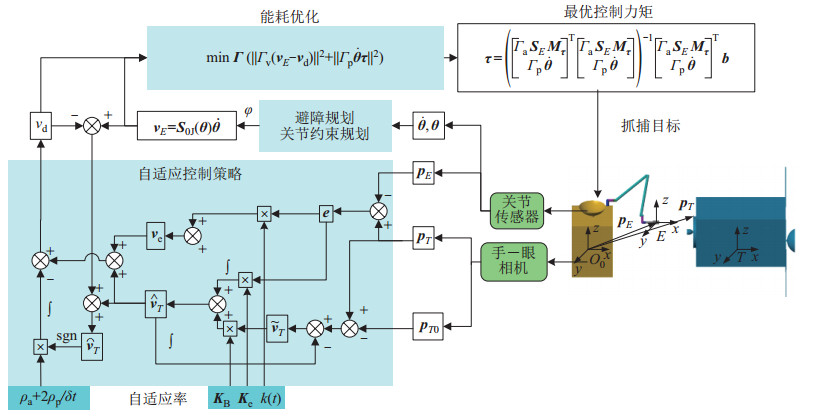
图 5 在最优能耗条件下实现目标捕获的自适应跟踪控制策略图 Fig.5 Block diagram of the adaptive control strategy for target capturing with optimal energy-consumption |
空间机器人动力学线性化的贡献在于用同一个解析表达式同时实现了对正、逆动力学的解算,具有准确的模型,不会对收敛性、稳定性产生影响。空间机器人跟踪目标的稳定性和收敛性取决于在一定约束条件下的最优问题式(37)。现给出了控制器的候选李雅普诺夫函数:
| $ \begin{align} V = \frac{1}{2}{\mathit{\boldsymbol{e}}^{\rm T}} {\mathit{\boldsymbol{e}}} + \frac{1}{2}{\tilde{{\mathit{\boldsymbol{v}}}}}_{{\rm f}}^{{\rm T}} {\mathit{\boldsymbol{K}}}_{{\rm e}}^{- 1} {{\tilde{{\mathit{\boldsymbol{v}}}}}_{{\rm f}}} \end{align} $ | (39) |
显然
| $ \begin{align} \dot V = {\mathit{\boldsymbol{e}}^{\rm T}} {\dot{{\mathit{\boldsymbol{e}}}}} + {\tilde{{\mathit{\boldsymbol{v}}}}}_T^{{\rm T}} {\mathit{\boldsymbol{K}}}_{{\rm e}}^{- 1}{\dot{\tilde{{\mathit{\boldsymbol{v}}}}}_T} \end{align} $ | (40) |
根据式(19)(31),末端执行器的最优速度为
| $ \begin{align} {{\mathit{\boldsymbol{v}}}_E} = k(t){\mathit{\boldsymbol{e}}} + \overset\frown{\boldsymbol{v}} _T \end{align} $ | (41) |
位姿误差导数和速度估计偏差导数分别为
| $ \begin{align} {\dot{{\mathit{\boldsymbol{e}}}}} &= {\mathit{\boldsymbol{v}}_T} - k(t){\mathit{\boldsymbol{e}}} - \overset\frown{\boldsymbol{v}} _{T} \end{align} $ | (42a) |
| $ \begin{align} {\dot{\tilde{{\mathit{\boldsymbol{v}}}}}_T} &= {{\dot{{\mathit{\boldsymbol{v}}}}}_T} - {{\dot{\hat{{\mathit{\boldsymbol{v}}}}}}_T} + {\rm{sgn}} \overset\frown{\boldsymbol{v}} _{T} \left({{\rho_{\rm a}} + \frac{{2{\rho_{\rm p}}}}{{\delta t}}}\right) - {\dot{\varDelta}_{\rm p}} \end{align} $ | (42b) |
将式(42) 代入式(40) 可得
| $ \begin{align} \dot V =\;& {\mathit{\boldsymbol{e}}^{\rm T}} ({{\mathit{\boldsymbol{v}}_T} - k(t){\mathit{\boldsymbol{e}}} - \overset\frown{\boldsymbol{v}} _{T}}) + \\ & {\tilde{{\mathit{\boldsymbol{v}}}}}_T^{\rm T} \mathit{\boldsymbol{K}}_{\rm e}^{- 1} \left[{{{{\dot{{\mathit{\boldsymbol{v}}}}}}_T} - {\dot{\hat{{\mathit{\boldsymbol{v}}}}}}_T+ {\rm{sgn}} \overset\frown{\boldsymbol{v}} _{T} \left({{\rho_{\rm a}} + \frac{{2{\rho_{\rm p}}}}{{\delta t}}}\right) - {{{\dot{\varDelta}}}_{\rm p}}}\right] \\ =\;& - k(t){\mathit{\boldsymbol{e}}^{\rm T}} {\mathit{\boldsymbol{e}}} - {\tilde{{\mathit{\boldsymbol{v}}}}}_T^{\rm T} \mathit{\boldsymbol{K}}_{\rm e}^{- 1}{\mathit{\boldsymbol{K}}_{\rm B}} {{{\tilde{{\mathit{\boldsymbol{v}}}}}}_T}+ \\ & {\tilde{{\mathit{\boldsymbol{v}}}}}_T^{\rm T} \mathit{\boldsymbol{K}}_{\rm e}^{- 1} \left[{{{{\dot{{\mathit{\boldsymbol{v}}}}}}_T} - {{{\dot{\varDelta}}}_{\rm p}} + {\rm{sgn}} \overset\frown{\boldsymbol{v}} _{T} \left({{\rho_{\rm a}} + \frac{{2{\rho_{\rm p}}}}{{\delta t}}}\right)}\right] \end{align} $ | (43) |
根据式(29),可得
| $ \begin{align} | {{\dot{\varDelta}_{\rm p}}} |= \frac{{{\rm d}| {{\mathit{\boldsymbol{v}}_E} - {\mathit{\boldsymbol{v}}_{\rm d}}} |}}{{{\rm d}t}} \leqslant \frac{{2{\rho_{\rm p}}}}{{\delta t}} \end{align} $ | (44) |
显然,
| $ \begin{align} \overset\frown{\boldsymbol{v}} _{T}^{\rm T} ({{\dot{{\mathit{\boldsymbol{v}}}}_T} + {\rm{sgn}} \overset\frown{\boldsymbol{v}} _{T}{\rho_{\rm a}}}) & = | { \overset\frown{\boldsymbol{v}} _{T}^{\rm T}} || {{{{\dot{{\mathit{\boldsymbol{v}}}}}}_T} + {\rm{sgn}} \overset\frown{\boldsymbol{v}} _{T}{\rho_{\rm a}}} | \end{align} $ | (45) |
| $ \begin{align} \overset\frown{\boldsymbol{v}} _{T}^{\rm T} \left({{\rm{sgn}} \overset\frown{\boldsymbol{v}} _{T}\frac{{2{\rho_{\rm p}}}}{{\delta t}} - {\dot{\varDelta}_{\rm p}}}\right) & = | { \overset\frown{\boldsymbol{v}} _{T}^{\rm T}} | \left| {\rm{sgn}} \overset\frown{\boldsymbol{v}} _{T}\frac{{2{\rho_{\rm p}}}}{{\delta t}} - {{{\dot{\varDelta}}}_{\rm p}} \right| \end{align} $ | (46) |
将式(45)(46) 代入式(43) 可得
| $ \begin{align} \dot V=& - k(t){\mathit{\boldsymbol{e}}^{\rm T}} {\mathit{\boldsymbol{e}}} - {\tilde{{\mathit{\boldsymbol{v}}}}}_T^{\rm T} \mathit{\boldsymbol{K}}_{\rm e}^{- 1}{\mathit{\boldsymbol{K}}_{\rm B}} {{{\tilde{{\mathit{\boldsymbol{v}}}}}}_T}- \\ & | { \overset\frown{\boldsymbol{v}} _{T}^{\rm T}} |\mathit{\boldsymbol{K}}_{\rm e}^{- 1} \left| - {{{\dot{\varDelta}}}_{\rm p}} + {\rm{sgn}} \overset\frown{\boldsymbol{v}} _{T}\frac{{2{\rho_{\rm p}}}}{{\delta t}} \right| - \\ & | { \overset\frown{\boldsymbol{v}} _{T}^{\rm T}} |\mathit{\boldsymbol{K}}_{\rm e}^{- 1}| {{{{\dot{{\mathit{\boldsymbol{v}}}}}}_T}+ {\rm{sgn}} \overset\frown{\boldsymbol{v}} _{T}{\rho_{\rm a}}} | + o({\mathit{\boldsymbol{v}}_T}) \end{align} $ | (47) |
其中
本研究旨在控制机械臂在各种约束条件下以最小的能耗、最小的误差跟踪期望轨迹,实现对目标的捕获。本文从精度、效率和能耗等方面分析了该控制器的性能,通过数值仿真研究了利用带有SSRMS型机械臂的空间机器人捕获失效目标时的控制器性能。所有的案例研究均采用软件进行,采样周期为0.1 s。在如下3种假设下进行仿真:1) 有外部干扰(如重力梯度);2) 机械臂与底座均为刚体;3) 末端执行器捕获目标后机械臂无碰撞地连接目标。假设目标的姿态可以通过手眼视觉系统获得。图 6展示了空间机器人和目标在接近阶段的初始状态。

|
图 6 空间机器人捕获失效目标时的初始状态 Fig.6 state of the space robot capturing a defunct target |
空间机器人飞行器坐标系
|
|
表 1 空间机器人的运动学和动力学参数 Tab. 1 Kinematic and dynamic parameters of the space robot |
式(21) 参数选定为
| $ \begin{align} {\mathit{\boldsymbol{k}}_v}(t)& = [{{k_v}(t)} \; \; {{k_\omega}(t)}]\\ {k_v}(t) & = \begin{cases} \dfrac{{| {{\underline{\mathit{\boldsymbol{v}}}_{{{\rm e}} v}}} |}}{{| {\mathit{\boldsymbol{e}}} |}}, & \dfrac{{| {{\underline{\mathit{\boldsymbol{v}}}_{{{\rm e}} v}}} |}}{{| {\mathit{\boldsymbol{e}}} |}} < \dfrac{{{r_{\rm e}}}}{{| {\mathit{\boldsymbol{e}}} |}}\\ 0.6, & \dfrac{{| {{\underline{\mathit{\boldsymbol{v}}}_{{{\rm e}} v}}} |}}{{| {\mathit{\boldsymbol{e}}} |}} \geqslant \dfrac{{{r_{\rm e}}}}{{| {\mathit{\boldsymbol{e}}} |}} \end{cases} \\ {k_\omega} (t) & = \begin{cases} \dfrac{{| {{\underline{\mathit{\boldsymbol{v}}}_{{{\rm e}} \omega}}} |}}{{| {\mathit{\boldsymbol{e}}} |}}, & \dfrac{{| {{\underline{\mathit{\boldsymbol{v}}}_{{{\rm e}} \omega}}} |}}{{| {\mathit{\boldsymbol{e}}} |}} < \dfrac{{{\theta_{\rm e}}}}{{| {\mathit{\boldsymbol{e}}} |}} \\ 0.5, & \dfrac{{| {{\underline{\mathit{\boldsymbol{v}}}_{{{\rm e}} \omega}}} |}}{{| {\mathit{\boldsymbol{e}}} |}} \geqslant \dfrac{{{r_{\rm e}}}}{{| {\mathit{\boldsymbol{e}}} |}} \end{cases} \end{align} $ | (48) |
其中
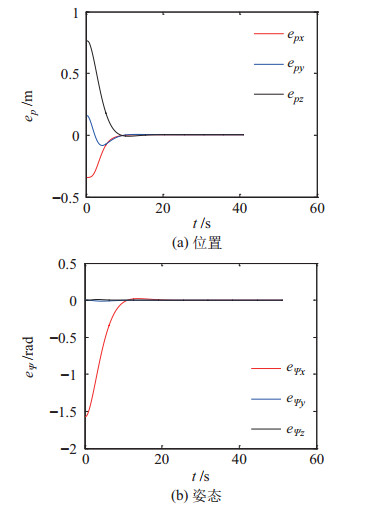
工况1的抵达时间
|
图 7 工况1:末端执行器与目标静态捕获点之间的跟踪误差 Fig.7 Case 1: the tracking error between the end-effector and the static capturing point of the target |
|
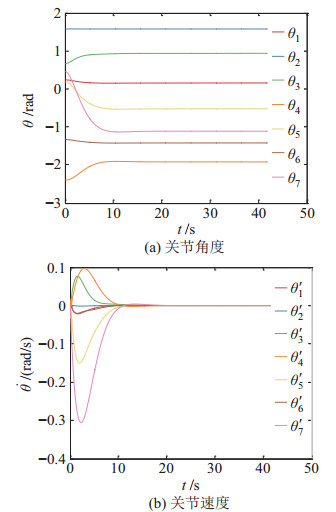
图 8 工况1:关节角度和速度的时间历程 Fig.8 Case 1: time histories of the joint angles and velocities |
|
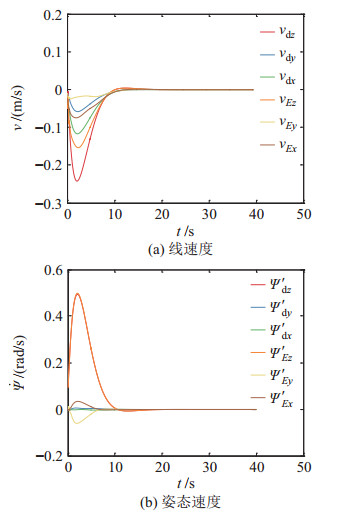
图 9 工况1:经本文控制器调节后末端执行器速度的时间历程和期望速度 Fig.9 Case 1: time histories of the end-effector velocity regulated by the proposed controller and the desired velocity |
|
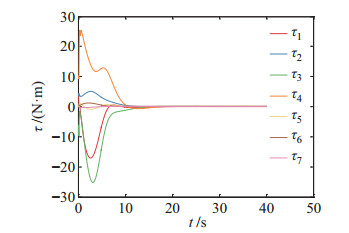
图 10 工况1:控制器优化后的关节力矩 Fig.10 Case 1: joint torques optimized by the controller |
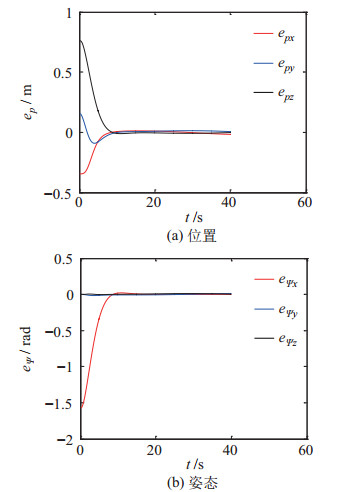
工况2的抵达时间
|
图 11 工况2:末端执行器与目标动态捕获点之间的跟踪误差 Fig.11 Case 2: the tracking error between the end-effector and the dynamic capturing point of the target |
关节角度和关节速度变化过程如图 12所示,关节轨迹平滑,关节速度稳定。图 13对比了末端执行器速度

|
图 12 工况2:关节角度和速度的变化历程 Fig.12 Case 2: time histories of the joint angles and velocities |
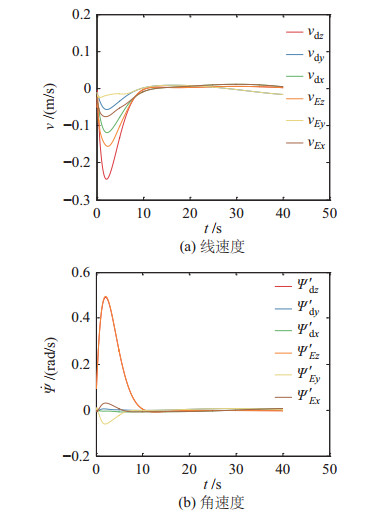
|
图 13 工况2:末端执行器速度的时间历程和期望速度 Fig.13 Case 2: time histories of the end-effector velocity and the desired velocity |
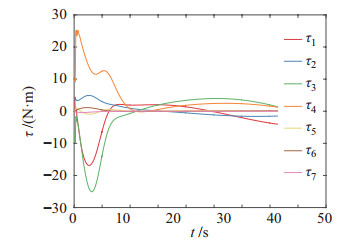
|
图 14 工况2:最优关节力矩 Fig.14 Case 2: optimal joint torques |
从这些图中可以看出,规划轨迹和约束都得以实现。图 15给出了采用所设计的控制策略后机械臂在避障和接近动态抓捕点的过程中每一个时刻的构形。它直观地说明了空间机器人末端执行器可到达捕获点并避免碰撞。图 15(b)隐藏了飞行器和目标,以便清晰地展示接近和跟踪阶段的构形。

|
图 15 工况2的接近和跟踪阶段 Fig.15 The approaching and tracking phases for Case 2 |
工况1的计算代码是在Win10操作系统上执行的,系统采用主频为2.30 GHz的Intel® Core
为了验证该控制器在控制器优化问题中的求解效率优势,将该方法与2个方法进行了比较,分别是文[27]提出的基于凸优化的轨迹规划方案(COTP)和文[22]提出的改进的最优积分滑模控制(OISMC)。COTP方法使用关节速度作为决策变量,产生的轨迹规划问题用凸二次规划法求解。OISMC方法是一种能耗效率高、计算复杂度低的控制方法。在捕获阶段,控制器执行400次优化,平均每次优化计算时间为14.1 ms。表 2比较了上述3种方法在每次优化迭代中的计算效率。以上分析通过比较各优化算法的平均解算时间来说明各控制算法的计算复杂度。
|
|
表 2 3种方法的计算效率对比 Tab. 2 Computation time of the three methods |
采用能耗模型直观地反映了其优化的效果。这里提出一个测量能耗的方法:
| $ \begin{align} f= \int_0^{{t_{\rm f}}} \dot{\theta}{}^{\rm T} \mathit{\boldsymbol{\tau}} {\rm d}t \end{align} $ | (49) |
以工况1为例,其能耗结果如图 16所示。结果表明,在未进行优化的情况下,所提控制策略的能耗要小于采用相同控制策略但不优化能耗的方法,能量效率提高75%。
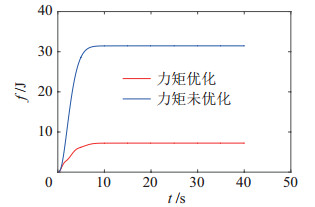
|
图 16 对工况1进行能耗优化和不进行能耗优化情况下所设计控制器的能耗 Fig.16 Energy consumption of the proposed controller with and without energy optimization for Case 1 |
实验中空间机器人基座固定在平台上,机械臂和目标星模拟器均位于气浮台上,抓捕运动、目标星模拟器运动均处于同一平面,通过零重力气浮装置支撑在气浮台上,保证实现空间无重力情况的等效模拟。机械臂关节3、关节4、关节5可以运动。目标星的运动模拟了空间章动在气浮台平面的投影轨迹,进行了抓捕的等效实验。空间机器人在最优能耗条件下进行目标捕获的地面等效实验的布局如图 17所示。目标星做摆动角为12

|
图 17 空间机器人在最优能耗条件下进行目标捕获的地面等效实验 Fig.17 Ground equivalent experiment of the space robot capturing the target with optimal energy-consumption |
利用本文提出的控制策略,空间机器人能够以最优的能耗有效地跟踪目标,如图 18所示。前70 s是接近跟踪过程,之后机械臂与目标星发生接触、形成复合体,产生了力矩的波动。从图 19~图 21可以看出,在接近跟踪过程,即前70 s,本文方法的跟踪精度可以达到0.75
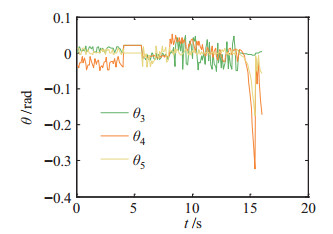
|
图 18 基于最优能耗的自适应跟踪控制策略下关节3~5的角度跟踪误差 Fig.18 Angle tracking errors of the 3rd |
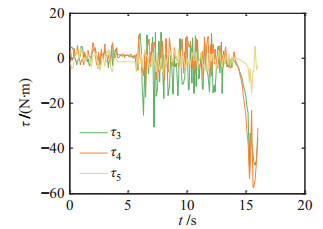
|
图 19 基于最优能耗的自适应跟踪控制策略下关节3~5的力矩 Fig.19 Torques of the 3rd |

|
图 20 自适应跟踪控制策略下关节3~5的角度跟踪误差 Fig.20 Angle tracking errors of the 3rd |
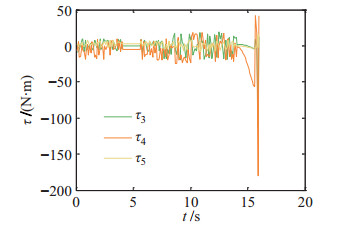
|
图 21 自适应跟踪控制策略下关节3~5的力矩 Fig.21 Torques of the 3rd~5th joints in the adaptive tracking control strategy |
提出了一种可以优化能耗的自适应跟踪控制器,可以在耦合、非线性、不确定性、障碍和一系列关节限制等约束下实现目标跟踪和捕获。该控制方法在关节空间中转化为具有线性等式和不等式约束的二次规划问题。引入了方位角
| [1] |
Shan M H, Guo J, Gill E. Review and comparison of active space debris capturing and removal methods[J]. Progress in Aerospace Sciences, 2016, 80: 18-32. DOI:10.1016/j.paerosci.2015.11.001 |
| [2] |
May G, Barletta I, Stahl B, et al. Energy management in production: A novel method to develop key performance indicators for improving energy efficiency[J]. Applied Energy, 2015, 149: 46-61. DOI:10.1016/j.apenergy.2015.03.065 |
| [3] |
Zhou Y Q, Luo J J, Wang M M. Dynamic coupling analysis of multi-arm space robot[J]. Acta Astronautica, 2019, 160: 583-593. DOI:10.1016/j.actaastro.2019.02.017 |
| [4] |
Aghili F, Parsa K. An adaptive vision system for guidance of a robotic manipulator to capture a tumbling satellite with unknown dynamics[C]//IEEE/RSJ International Conference on Intelligent Robots and Systems. Piscataway, USA: IEEE, 2008: 3064-3071.
|
| [5] |
Aghili F, Parsa K. An adaptive Kalman filter for motion esitmation/prediction of a free-falling space object using laser-vision data with uncertain inertial and noise characteristics[C]//AIAA Guidance, Navigation and Control Conference and Exhibit. Reston, USA: AIAA, 2008. DOI: 10.2514/6.2008-7317.
|
| [6] |
Shi L L, Kayastha S, Katupitiya J. Robust coordinated control of a dual-arm space robot[J]. Acta Astronautica, 2017, 138: 475-489. DOI:10.1016/j.actaastro.2017.06.009 |
| [7] |
Zhang B, Liang B, Wang X, et al. Manipulability measure of dual-arm space robot and its application to design an optimal configuration[J]. Acta Astronautica, 2016, 128: 322-329. DOI:10.1016/j.actaastro.2016.07.040 |
| [8] |
Shi L L, Jayakody H, Katupitiya J, et al. Coordinated control of a dual-arm space robot: Novel models and simulations for robotic control methods[J]. IEEE Robotics & Automation Magazine, 2018, 25(4): 86-95. |
| [9] |
Wang H L, Xie Y C. Prediction error based adaptive Jacobian tracking for free-floating space manipulators[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 3207-3221. DOI:10.1109/TAES.2012.6324694 |
| [10] |
Talebi H A, Khorasani K, Tafazoli S. A recurrent neuralnetwork-based sensor and actuator fault detection and isolation for nonlinear systems with application to the satellite's attitude control subsystem[J]. IEEE Transactions on Neural Networks, 2009, 20(1): 45-60. DOI:10.1109/TNN.2008.2004373 |
| [11] |
Zhang Y Y, Chen S Y, Li S, et al. Adaptive projection neural network for kinematic control of redundant manipulators with unknown physical parameters[J]. IEEE Transactions on Industrial Electronics, 2018, 65(6): 4909-4920. DOI:10.1109/TIE.2017.2774720 |
| [12] |
Zhou Z-G, Zhang Y-A, Zhou D. Robust prescribed performance tracking control for free-floating space manipulators with kinematic and dynamic uncertainty[J]. Aerospace Science and Technology, 2017, 71: 568-579. DOI:10.1016/j.ast.2017.10.013 |
| [13] |
Wang H S, Guo D J, Xu H, et al. Eye-in-hand tracking control of a free-floating space manipulator[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(4): 1855-1865. DOI:10.1109/TAES.2017.2674218 |
| [14] |
董楸煌, 陈力. 柔性空间机械臂捕获卫星过程的鲁棒镇定与自适应抑振复合控制[J]. 机器人, 2014, 36(3): 342-348. Dong Q H, Chen L. Composite control of robust stabilization and adaptive vibration suppression of flexible space manipulator capturing a satellite[J]. Robot, 2014, 36(3): 342-348. |
| [15] |
张博, 梁斌, 王学谦, 等. 双臂空间机器人可操作度分析及其构型优化[J]. 宇航学报, 2016, 37(10): 1207-1214. Zhang B, Liang B, Wang X Q, et al. Manipulability measure of a dual-arm space robot and its application to configuration optimization[J]. Journal of Astronautics, 2016, 37(10): 1207-1214. DOI:10.3873/j.issn.1000-1328.2016.10.008 |
| [16] |
Giordano A M, Ott C, Albu-Schaffer A. Coordinated control of spacecraft's attitude and end-effector for space robots[J]. IEEE Robotics and Automation Letters, 2019, 4(2): 2108-2115. DOI:10.1109/LRA.2019.2899433 |
| [17] |
Nanos K, Papadopoulos E. Avoiding dynamic singularities in Cartesian motions of free-floating manipulators[J]. IEEE Transactions on Aerospace and Electronic Systems, 2015, 51(3): 2305-2318. DOI:10.1109/TAES.2015.140343 |
| [18] |
Leigsnering M, Ahmad F, Amin M G, et al. Parametric dictionary learning for sparsity-based TWRI in multipath environ ments[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(2): 532-547. |
| [19] |
Pisculli A, Felicetti L, Gasoverlineri P, et al. A reaction-null/Jacobian transpose control strategy with gravity gradient compensation for on-orbit space manipulators[J]. Aerospace Science and Technology, 2014, 38: 30-40. DOI:10.1016/j.ast.2014.07.012 |
| [20] |
Peng J Q, Xu W F, Pan E Z, et al. Dual-arm coordinated capturing of an unknown tumbling target based on efficient parameters estimation[J]. Acta Astronautica, 2019, 162: 589-607. |
| [21] |
Zhang B, Liang B, Wang Z W, et al. Coordinated stabilization for space robot after capturing a noncooperative target with large inertia[J]. Acta Astronautica, 2017, 134: 75-84. |
| [22] |
Norsahperi N M H, Danapalasingam K A. An improved optimal integral sliding mode control for uncertain robotic manipulators with reduced tracking error, chattering, and energy consumption[J]. Mechanical Systems and Signal Processing, 2020, 142. DOI:10.1016/j.ymssp.2020.106747 |
| [23] |
de Stefano M, Mishra H, Balachandran R, et al. Multi-rate tracking control for a space robot on a controlled satellite: A passivity-based strategy[J]. IEEE Robotics and Automation Letters, 2019, 4(2): 1319-1326. |
| [24] |
Jin M H, Liu Q, Wang B, et al. An efficient and accurate inverse kinematics for 7-DOF redundant manipulators based on a hybrid of analytical and numerical method[J]. IEEE Access, 2020, 8: 16316-16330. |
| [25] |
Jia Y H, Misra A K. Robust trajectory tracking control of a dualarm space robot actuated by control moment gyroscopes[J]. Acta Astronautica, 2017, 137: 287-301. |
| [26] |
Rimon E, Boyd S P. Obstacle collision detection using best ellipsoid fit[J]. Journal of Intelligent and Robotic Systems, 1997, 18(2): 105-126. |
| [27] |
Yang S J, Wen H, Jin D P. Trajectory planning of dual-arm space robots for target capturing and base manoeuvring[J]. Acta Astronautica, 2019, 164: 142-151. |
 2022, Vol. 44
2022, Vol. 44


