2. 西北工业大学航天飞行力学技术重点实验室, 陕西 西安 710072
2. National Key Laboratory of Aerospace Flight Dynamics, Northwestern Polytechnical University, Xi'an 710072, China
空间绳系系统(space tethered system,STS)是指借助柔性系绳将2个或2个以上的空间卫星/机器人连接在一起的刚柔耦合群体系统。作为一种新型航天器,STS在灵活性、生命周期和功能拓展性等方面优势显著[1-2],成为近年来国内外航天领域的研究热点。其在空间垃圾清除[3]、空间观测[4]以及太空电梯[5]等方面具有广阔的应用前景。
STS动力学建模的难点在于柔性系绳的建模,常用的有杆模型[6]、珠点模型[7]和连续体模型[8]等。研究者利用以上3种模型开展了大量研究。黄攀峰等[9-12]提出了一种空间绳系机器人,其可看作由柔性系绳将抓捕器与空间平台相连组成的二体STS,可广泛应用于空间在轨维护、在轨加注和空间碎片清除等任务中,并对系统的动力学建模和稳定控制等方面展开了深入研究。Yousefian等[13]针对二体STS的摆动抑制问题,采用扩展卡尔曼滤波算法估计系绳的实时摆角用于控制器的状态反馈。Chung[14]针对NASA(美国国家航空航天局)的宇宙结构进化亚毫米深空探测器工程提出了三体STS,并设计了相对状态感知器用于实时反馈受控系统的相对位姿状态。Misra[15]、Li[16]、史格非[17]、王振坤[18]等针对空间天梯系统存在单个或多个攀爬器时系统的动力学特性和摆动控制进行了研究。Netzer等[19]针对直链式多体STS设计了降阶观测器用于估计相邻系绳单元之间的曲率角。方国涛等[20]针对双金字塔STS在状态保持阶段的状态估计问题,提出了一种最少传感器布局下的状态估计方法。
精确的运动状态测量与估计是空间系统导航、控制与应用的前提。目前有关STS的研究主要集中于系统的动力学分析和稳定控制方面,而关于STS状态估计的研究相对较少。柔性系绳连接的存在,造就了不同于传统空间编队系统的全新状态估计问题。一方面,柔性系绳连接能够提供系统运动状态之间有价值的耦合约束关系,如何充分利用系绳-卫星之间的耦合约束关系,增强系统状态感知效能,优化系统传感器布局以降低成本[21],是STS状态感知亟待解决的难题,而现有研究[13-14, 19]均未考虑柔性系绳连接约束。另一方面,STS是一个多维、大尺度、刚柔耦合的能量耗散系统,系统的应用涉及系绳的伸展、收回等复杂过程,并且由于卫星之间存在柔性系绳约束,因此STS的轨道运动与系统姿态运动存在耦合关系[22-23],这为系统的高精度状态估计带来挑战。
针对含约束的系统状态估计,国内外学者已开展了大量的研究。目前处理含有等式约束信息的状态估计的方法主要有伪测量法[24]、投影法[25]以及降维法[26]等。其中,伪测量法将系统的状态约束视为“精确”测量值,然后将该测量值与同时刻的量测方程放在一起进行扩维,得到一个新的观测方程,从而将约束系统转变为一个无约束动态方程,最后应用卡尔曼滤波进行状态估计。该方法因简单有效已被广泛应用于目标跟踪、经济模型等领域。但扩维后的新噪声协方差为奇异矩阵,在进行滤波时会引起数值发散问题[27-28]。
本文针对一类直链式
本文研究的直链式

|
图 1 直链式N体空间绳系系统模型示意图 Fig.1 Model diagram of linear N-body space tethered system |
(1) 相对于系绳长度,卫星大小可忽略,因此所有卫星均假设为质点;
(2) 空间系绳假设为无质量刚性杆;
(3) 系统运行于圆形开普勒轨道,除了地球引力,其他外界干扰均忽略。
2.2 基于Udwadia-Kalaba方法的STS动力学建模STS是多参数耦合的约束系统,一般的系统建模方法有牛顿法、拉格朗日法和凯恩法等。其中,牛顿法推导简单,但未知数和方程数目多,当刚体个数较多时,解耦过程困难;其他方法均需要在建模过程中引入中间变量,计算复杂。为此,本文基于Udwadia-Kalaba方法建立直链式
基于Udwadia-Kalaba方法的系统动力学建模一般遵循以下3个步骤:
步骤1:通过牛顿-欧拉法或拉格朗日法建立无约束多体系统方程
本文采用拉格朗日法对无约束直链式
| $ \begin{align} E_{\rm k} =\sum\limits_{i=1}^N {\frac{1}{2}m_{i} | {\dot{{\mathit{\boldsymbol{r}}}}_{i}} |^{2}} \end{align} $ | (1) |
式中,
同样,系统的势能可表示为
| $ \begin{align} E_{\rm p} =-\sum _{i=1}^N {GM_{\rm E} \frac{m_{i}} {| {{\mathit{\boldsymbol{r}}}_{i}} |}} \end{align} $ | (2) |
式中,
将式(1)(2) 代入第二类拉格朗日方程,可得到系统的无约束动力学方程为
| $ \begin{align} m_{i} \mathit{\boldsymbol{\ddot{r}}}_{i} +\frac{\mu m_{i} \mathit{\boldsymbol{r}}_{i}} {| {\mathit{\boldsymbol{r}}_{i}} |^{3}}=\mathit{\boldsymbol{Q}}_{ri}, \quad i=1, 2, \cdots, N \end{align} $ | (3) |
式中,
由式(3) 可得到无约束力作用时的系统加速度:
| $ \begin{align} {\mathit{\boldsymbol{a}}} \triangleq \mathit{\boldsymbol{\ddot{q}}} =\mathit{\boldsymbol{M}}^{-1}{\mathit{\boldsymbol{Q}}}^{\rm (u)}({{\mathit{\boldsymbol{q}}}, {\mathit{\boldsymbol{u}}}}) \end{align} $ | (4) |
式中,
步骤2:对无约束系统施加约束
对于直链式
| $ \begin{align} \mathit{\boldsymbol{L}}=[{l_{1}, l_{2}, \cdots, l_{N-1}}]^{\rm T} \end{align} $ | (5) |
其中,
将式(5) 对时间连续2次求导,可得到约束的2阶Pfaffian标准微分形式如下:
| $ \begin{align} \mathit{\boldsymbol{A\ddot{q}}}=\mathit{\boldsymbol{b}} \end{align} $ | (6) |
式中,
| $ \begin{align*} \mathit{\boldsymbol{A}} & =\begin{bmatrix} {\mathit{\boldsymbol{r}}_{1} -\mathit{\boldsymbol{r}}_{2}} & {\mathit{\boldsymbol{r}}_{2} -\mathit{\boldsymbol{r}}_{1}} & \cdots & {\mathit{\boldsymbol{0}}_{1\times 3}} & {\mathit{\boldsymbol{0}}_{1\times 3}} \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ {\mathit{\boldsymbol{0}}_{1\times 3}} & {\mathit{\boldsymbol{0}}_{1\times 3}} & \cdots & {\mathit{\boldsymbol{r}}_{N-1} -\mathit{\boldsymbol{r}}_{N}} & {\mathit{\boldsymbol{r}}_{N} -\mathit{\boldsymbol{r}}_{N-1}} \end{bmatrix} \\ \mathit{\boldsymbol{b}} & =\begin{bmatrix} {\dot{l}_{t1}^{2} +l_{t1} \ddot{l}_{t1} -| {\mathit{\boldsymbol{\dot{r}}}_{1} -\mathit{\boldsymbol{\dot{r}}}_{2}} |^{2}} \\ \vdots \\ {\dot{l}_{t(N-1)}^{2} +l_{t(N-1)} \ddot{l}_{t(N-1)} -| {\mathit{\boldsymbol{\dot{r}}}_{N-1} -\mathit{\boldsymbol{\dot{r}}}_{N}} |^{2}} \end{bmatrix} \end{align*} $ |
其中,
步骤3:约束力求解
在已知广义力
| $ \begin{align} \mathit{\boldsymbol{M}}\mathit{\boldsymbol{\ddot{q}}}={\mathit{\boldsymbol{Q}}}^{\rm (u)}( {{\mathit{\boldsymbol{q}}}, {\mathit{\boldsymbol{u}}}})+{\mathit{\boldsymbol{Q}}}^{\rm (c)}( {{\mathit{\boldsymbol{q}}}}) \end{align} $ | (7) |
其中,系统约束力
系统的两端卫星的绝对位置
| $ \begin{align} \mathit{\boldsymbol{r}}_{i}^{\rm (g)} =\mathit{\boldsymbol{r}}_{i} +\mathit{\boldsymbol{v}}^{\rm (g)} \end{align} $ | (8) |
式中,
系绳的绳长作为有价值的先验信息,需要加以考虑。本文中将系绳的绳长约束表示为
| $ \begin{align} \mathit{\boldsymbol{z}}^{(l)}=\mathit{\boldsymbol{L}}({\mathit{\boldsymbol{q}}})+\mathit{\boldsymbol{v}}^{(l)} \end{align} $ | (9) |
式中,
| $ \begin{align} \mathit{\boldsymbol{\dot{v}}}^{(l)}=-\mathit{\boldsymbol{Q}}^{(l)}\mathit{\boldsymbol{b}}^{(l)}+\mathit{\boldsymbol{u}}^{(l)} \end{align} $ | (10) |
其中,
需要注意的是,实际情况中系绳形变很小,相对于系绳绳长可忽略。诚然系绳形变很小,但是确实存在,此处将考虑系绳小形变并将其建模为虚拟噪声
本文提出的状态估计框架如图 2所示。首先基于Udwadia-Kalaba方法建立系统的约束动力学模型。然后进行GPS传感器布局,基于伪测量法将系绳绳长视为“精确”的观测值并将该“精确”值与原观测方程组合形成新的观测方程,设计状态估计算法,进行可观测性分析。最后实现系统状态实时精确输出。
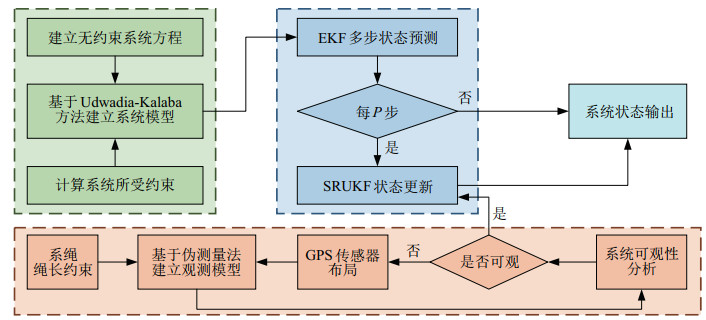
|
图 2 状态估计框架图 Fig.2 Framework of state estimation |
令
| $ \begin{align} \mathit{\boldsymbol{\dot{X}}} & =\frac{{\rm d}\mathit{\boldsymbol{X}}}{{\rm d}t} \\ & =\begin{bmatrix} {\mathit{\boldsymbol{\dot{q}}}} \\ {\mathit{\boldsymbol{M}}^{-1}[{\mathit{\boldsymbol{Q}}^{\rm (u)}( {\mathit{\boldsymbol{q}}, \mathit{\boldsymbol{u}}})+\mathit{\boldsymbol{A}}^{\rm T}( {\mathit{\boldsymbol{AM}}^{-1}\mathit{\boldsymbol{A}}^{\rm T}})^{+}({\mathit{\boldsymbol{b}}-\mathit{\boldsymbol{Aa}}})}]} \end{bmatrix} \end{align} $ | (11) |
将上式写成函数形式为
| $ \begin{align} \mathit{\boldsymbol{\dot{X}}}=\mathit{\boldsymbol{f}}({\mathit{\boldsymbol{X}}})+\mathit{\boldsymbol{\varGamma}} \end{align} $ | (12) |
式中,系统噪声
考虑系统的GPS传感器布局,则测量方程为
| $ \begin{align} \mathit{\boldsymbol{z}}^{\rm (g)}({\mathit{\boldsymbol{X}}})=\mathit{\boldsymbol{H}}_{g} \mathit{\boldsymbol{X}}^{\rm (g)}+\mathit{\boldsymbol{V}}^{\rm (g)} \end{align} $ | (13) |
式中,测量噪声
| $ \begin{align} \mathit{\boldsymbol{H}}_{g} = \begin{bmatrix} {\mathit{\boldsymbol{I}}_{3}} & \cdots & {\bm0_{3\times 3}} & {\bm0_{3\times (3N)}} \\ \vdots & \ddots & \vdots & \vdots \\ {\bm0_{3\times 3}} & \cdots & {\mathit{\boldsymbol{I}}_{3}} & {\bm0_{3\times (3N)}} \end{bmatrix} \end{align} $ | (14) |
式中,
基于伪测量法,将系绳绳长约束加入测量方程(13) 可得到
| $ \begin{align} \mathit{\boldsymbol{Z}}_{k} = \underbrace {\begin{bmatrix} {\mathit{\boldsymbol{z}}^{\rm (g)}} \\ {\mathit{\boldsymbol{z}}^{(l)}} \end{bmatrix}}_{\mathit{\boldsymbol{h}}({{{\mathit{\boldsymbol{X}}}}_{k}})}+ \underbrace{\begin{bmatrix} {\mathit{\boldsymbol{V}}^{\rm (g)}} \\ {\mathit{\boldsymbol{v}}^{(l)}} \end{bmatrix}}_{\bm\varUpsilon_{k}} \end{align} $ | (15) |
式中,
将式(12)(15) 联立可得系统的状态方程为
| $ \begin{align} \begin{cases} {\mathit{\boldsymbol{\dot{X}}}={\mathit{\boldsymbol{f}}}({\mathit{\boldsymbol{X}}})+\mathit{\boldsymbol{\varGamma}}} \\ {\mathit{\boldsymbol{Z}}_{k} =\mathit{\boldsymbol{h}}({\mathit{\boldsymbol{X}}_{k}})+\mathit{\boldsymbol{\varUpsilon}}_{k}} \end{cases} \end{align} $ | (16) |
为了实施滤波,首先需要对系统状态方程进行离散化处理:
| $ \begin{align} \begin{cases} \mathit{\boldsymbol{X}}_{k} =\mathit{\boldsymbol{X}}_{k-1} +\Delta T{\mathit{\boldsymbol{f}}} ({\mathit{\boldsymbol{X}}_{k-1}})+\mathit{\boldsymbol{\varGamma}}_{k-1} \\ \mathit{\boldsymbol{Z}}_{k} =\mathit{\boldsymbol{h}} ({\mathit{\boldsymbol{X}}_{k}})+\mathit{\boldsymbol{\varUpsilon}}_{k} \end{cases} \end{align} $ | (17) |
式中,
扩展卡尔曼滤波状态估计过程中雅可比矩阵计算复杂,而无迹卡尔曼滤波(UKF)存在因系统状态协方差矩阵无法实现Cholesky分解而导致滤波发散的问题[32-33]。为此,本文开发了一种改进平方根无迹卡尔曼滤波(improved square root unscented Kalman filter,IUKF)算法。该算法包含2部分:EKF(扩展卡尔曼滤波)多步状态预测部分和SRUKF(平方根无迹卡尔曼滤波)状态更新部分。IUKF算法计算步骤如下:
步骤1:Sigma点计算
| $ \begin{align} \begin{cases} \mathit{\boldsymbol{\varTheta}}_{k-1}^{(i)} =\hat{\mathit{\boldsymbol{X}}}_{k-1}, & i=0 \\ \mathit{\boldsymbol{\varTheta}}_{k-1}^{(i)} =\hat{\mathit{\boldsymbol{X}}}_{k-1} +({\eta \sqrt{\hat{\mathit{\boldsymbol{P}}}_{k-1}}})_{i}, & i=1, \cdots, n \\ \mathit{\boldsymbol{\varTheta}}_{k-1}^{(i)} =\hat{\mathit{\boldsymbol{X}}}_{k-1} -({\eta \sqrt{\hat{\mathit{\boldsymbol{P}}}_{k-1}}})_{i}, & i=n+1, \cdots, 2n \end{cases} \end{align} $ | (18) |
相应的权值为
| $ \begin{align} \begin{cases} W_{\rm m}^{(i)} =\dfrac{\lambda} {n+\lambda}, & {i=0} \\[5pt] W_{\rm c}^{(i)} =\dfrac{\lambda} {n+\lambda} +({1-\alpha^{2}+\beta}), & {i=0} \\[5pt] W_{\rm m}^{(i)} =W_{\rm c}^{(i)} =\dfrac{1}{2( {n+\lambda})}, & {i=1, \cdots, 2n} \end{cases} \end{align} $ | (19) |
式中,
步骤2:多步状态预测
| $ \begin{align} \hat{\mathit{\boldsymbol{X}}}_{k-1}^{(j)} =\hat{\mathit{\boldsymbol{X}}}_{k-1}^{(j-1)} +\Delta T\mathit{\boldsymbol{f}}({\hat{\mathit{\boldsymbol{X}}}_{k-1}^{(j-1)}}), \quad j=1, 2, \cdots, P \end{align} $ | (20) |
考虑到GPS传感器更新频率较低[34],无法满足航天器的实时导航需求,因此本文采用多步预测方法,即系统状态每预测
步骤3:时间更新
| $ \begin{align} & \hat{\mathit{\boldsymbol{\varTheta}}}_{k} =\hat{\mathit{\boldsymbol{X}}}_{k}^{({P})} \end{align} $ | (21) |
| $ \begin{align} & \hat{\mathit{\boldsymbol{X}}}_{k} =\sum _{i=0}^{2n} {W_{\rm m}^{(i)}} \hat{\mathit{\boldsymbol{\varTheta}}}_{k}^{(i)} \end{align} $ | (22) |
| $ \begin{align} & [{\mathit{\boldsymbol{\bar{Q}}}, {\mathit{\boldsymbol{S}}}_{k}^{-}}]\leftarrow \rm{qr} \\ & \left({\left[{\sqrt{W_{\rm c}^{(1)}} \left({\hat{\bm\varTheta}_{1:2n, k} - \left[{\underbrace {\hat{{\mathit{\boldsymbol{X}}}}_{k} \cdots \hat{{\mathit{\boldsymbol{X}}}}_{k}}_{2n}}\right]}\right)\sqrt{{\mathit{\boldsymbol{Q}}}_{k-1}^{(\Gamma)}}} \right]^{\rm T}, 0}\right) \end{align} $ | (23) |
| $ \begin{align} & {\mathit{\boldsymbol{S}}}_{k}^{-} \leftarrow {\rm{chol}} \left({{\mathit{\boldsymbol{S}}}_{k}^{-}, \sqrt{| {W_{\rm c}^{(0)}} |}({\hat{\bm\varTheta}_{0, k} -\hat{{\mathit{\boldsymbol{X}}}}_{k}}), {\rm{sgn}} W_{\rm c}^{(0)}}\right) \end{align} $ | (24) |
| $ \begin{align} & {\mathit{\boldsymbol{S}}}_{k}^{-} \leftarrow ({{\mathit{\boldsymbol{S}}}_{k}^{-}})^{\rm T} \end{align} $ | (25) |
| $ \begin{align} & \mathit{\boldsymbol{\varTheta}}_{k} =\left[{\underbrace {\hat{\mathit{\boldsymbol{X}}}_{k} \cdots \hat{\mathit{\boldsymbol{X}}}_{k}}_{2n+1}}\right]+\eta \left[{\mathit{\boldsymbol{0}}_{n, 1}} \; \; {\sqrt{\hat{\mathit{\boldsymbol{P}}}_{k}}} \; \; {-\sqrt{\hat{\mathit{\boldsymbol{P}}}_{k}}} \right] \end{align} $ | (26) |
| $ \begin{align} & \mathit{\boldsymbol{\varOmega}}_{k} =\mathit{\boldsymbol{h}}({\mathit{\boldsymbol{\varTheta}}_{k}}) \end{align} $ | (27) |
| $ \begin{align} & \hat{\mathit{\boldsymbol{Z}}}_{k} =\sum _{i=0}^{2n} {W_{\rm m}^{(i)}} \mathit{\boldsymbol{\varOmega}}_{k}^{(i)} \end{align} $ | (28) |
式中,“qr”与“chol”为Matlab函数,“sgn”为符号函数。
步骤4:测量更新
| $ \begin{align} & [{\mathit{\boldsymbol{\bar{Q}}}, {\mathit{\boldsymbol{S}}}_{\mathit{\boldsymbol{Z}}_{k}}} ]\leftarrow \\ & {\rm{qr}}\left({ \left[{\sqrt{{W}_{\rm c}^{( 1)}} \left({\mathit{\boldsymbol{\varOmega}}_{1:2n, k} - \left[{\underbrace {\hat{\mathit{\boldsymbol{Z}}}_{k} \cdots \hat{\mathit{\boldsymbol{Z}}}_{k}}_{2n}} \right]}\right)\sqrt{{\mathit{\boldsymbol{R}}}_{k}^{(\Upsilon)}}} \right]^{\rm T}, 0}\right) \end{align} $ | (29) |
| $ \begin{align} & {\mathit{\boldsymbol{S}}}_{\mathit{\boldsymbol{Z}}_{k}} \leftarrow \rm{chol} \left({{\mathit{\boldsymbol{S}}}_{\mathit{\boldsymbol{Z}}_{k}}, \sqrt{| {{W}_{\rm c}^{(0)}} |}({\mathit{\boldsymbol{\varOmega}}_{0, k} -\hat{\mathit{\boldsymbol{Z}}}_{k}}), {\rm{sgn}} {W}_{\rm c}^{(0)}}\right) \end{align} $ | (30) |
| $ \begin{align} & {\mathit{\boldsymbol{S}}}_{\mathit{\boldsymbol{Z}}_{k}} \leftarrow {\mathit{\boldsymbol{S}}}_{\mathit{\boldsymbol{Z}}_{k}}^{\rm T} \end{align} $ | (31) |
| $ \begin{align} & \mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{X}}_{k}, \mathit{\boldsymbol{Z}}_{k}} =\sum _{i=0}^{2n} {W_{\rm c}^{(i)}} ({\mathit{\boldsymbol{\varTheta}}_{k}^{(i)} -\hat{\mathit{\boldsymbol{Z}}}_{k}})({\mathit{\boldsymbol{\varTheta}}_{k}^{(i)} -\hat{\mathit{\boldsymbol{Z}}}_{k}})^{\rm T} \end{align} $ | (32) |
| $ \begin{align} & \mathit{\boldsymbol{K}}_{k} =\mathit{\boldsymbol{P}}_{\mathit{\boldsymbol{X}}_{k}, \mathit{\boldsymbol{Z}}_{k}} ({{\mathit{\boldsymbol{S}}}_{\mathit{\boldsymbol{Z}}_{k}}^{\rm T}})^{-1}{\mathit{\boldsymbol{S}}}_{\mathit{\boldsymbol{Z}}_{k}}^{-1} \end{align} $ | (33) |
| $ \begin{align} & \mathit{\boldsymbol{X}}_{k} =\hat{\mathit{\boldsymbol{X}}}_{k} +\mathit{\boldsymbol{K}}_{k} ( {\mathit{\boldsymbol{Z}}_{k} -\hat{\mathit{\boldsymbol{Z}}}_{k}}) \end{align} $ | (34) |
| $ \begin{align} & \mathit{\boldsymbol{U}}=\mathit{\boldsymbol{K}}_{k} {\mathit{\boldsymbol{S}}}_{\mathit{\boldsymbol{Z}}_{k}} \end{align} $ | (35) |
| $ \begin{align} & {\mathit{\boldsymbol{S}}}_{k} ={\rm{chol}}({\mathit{\boldsymbol{S}}}_{k}^{-}, \mathit{\boldsymbol{U}}, {\tt'}-') \end{align} $ | (36) |
本文研究的直链式
考虑如下无限平滑的非线性系统:
| $ \begin{align} \begin{cases} {\mathit{\boldsymbol{\dot{x}}} = {\mathit{\boldsymbol{f}}}({\mathit{\boldsymbol{x}}, \mathit{\boldsymbol{u}}})} \\ {\mathit{\boldsymbol{y}}={\mathit{\boldsymbol{h}}}({\mathit{\boldsymbol{x}}})} \end{cases} \end{align} $ | (37) |
式中
如果过程函数
| $ \begin{align} \begin{cases} {\mathit{\boldsymbol{\dot{x}}} = {\mathit{\boldsymbol{f}}}_{0} ({\mathit{\boldsymbol{x}}})+{\mathit{\boldsymbol{f}}}_{1} ({\mathit{\boldsymbol{x}}})u_{1} +\cdots +{\mathit{\boldsymbol{f}}}_{l} ({\mathit{\boldsymbol{x}}})u_{l}} \\ {\mathit{\boldsymbol{y}}={\mathit{\boldsymbol{h}}}({\mathit{\boldsymbol{x}}})} \end{cases} \end{align} $ | (38) |
式中,
定义1:函数
| $ \begin{align} \begin{cases} {L_{{\mathit{\boldsymbol{f}}}_{i}}^{0} h_{k} ({{\mathit{\boldsymbol{x}}}})=h_{k} ({{\mathit{\boldsymbol{x}}}})} \\[3pt] {L_{{\mathit{\boldsymbol{f}}}_{i}}^{k} h_{k} ({{\mathit{\boldsymbol{x}}}})=\dfrac{\partial ({L_{{\mathit{\boldsymbol{f}}}_{i}}^{k-1} h_{k} ( {{\mathit{\boldsymbol{x}}}})})}{\partial \mathit{\boldsymbol{x}}}{\mathit{\boldsymbol{f}}}_{i} ({\mathit{\boldsymbol{x}}})} \end{cases}\kern-15pt, \quad k=1, 2, \cdots \end{align} $ | (39) |
定义2:函数
| $ \begin{align} L_{{\mathit{\boldsymbol{f}}}_{j} {\mathit{\boldsymbol{f}}}_{i}}^{k} h_{k} ({\mathit{\boldsymbol{x}}})=L_{{\mathit{\boldsymbol{f}}}_{j}}^{1} ({L_{{\mathit{\boldsymbol{f}}}_{{i}}}^{k-1} h_{k} ({\mathit{\boldsymbol{x}}})})=\nabla L_{{\mathit{\boldsymbol{f}}}_{\mathit{\boldsymbol{i}}}}^{k-1} h_{k} ({\mathit{\boldsymbol{x}}})\cdot {\mathit{\boldsymbol{f}}}_{j} \end{align} $ | (40) |
基于上述李导数表示,可观性矩阵由李导数求导的行向量组成,可定义为
| $ \begin{align} \mathit{\boldsymbol{O}} \triangleq \begin{bmatrix}\nabla L^0 h_{k} ({\mathit{\boldsymbol{x}}})\\ \vdots\\ \nabla L_{{\mathit{\boldsymbol{f}}}_{i} \cdots {\mathit{\boldsymbol{f}}}_{j}}^{l} h_{k} ({\mathit{\boldsymbol{x}}})\end{bmatrix} \end{align} $ | (41) |
其中,
命题(可观性秩判据):如果式(41) 中定义的非线性系统可观性矩阵
推论:由于非线性系统(37) 是无限平滑的,可观性矩阵
注意:关于如何选择合适的李导数以及对应的
下面,将采用数学归纳法递推证明非线性系统(16) 的可观性。
首先,如果
| $ \begin{align} \begin{cases} {\mathit{\boldsymbol{\dot{X}}}\mathit{\boldsymbol{=f}}_{0} ({\mathit{\boldsymbol{X}}})+\mathit{\boldsymbol{f}}_{1} ({\mathit{\boldsymbol{X}}})u_{1} +\cdots +\mathit{\boldsymbol{f}}_{9} ({\mathit{\boldsymbol{X}}})u_{9}} \\ {\mathit{\boldsymbol{Z}}=\mathit{\boldsymbol{h}}({\mathit{\boldsymbol{X}}})} \end{cases} \end{align} $ | (42) |
式中
1) 0阶李导数
由定义1可知,函数的0阶李导数是函数本身
| $ \begin{align} L^{0}\mathit{\boldsymbol{h}}({\mathit{\boldsymbol{X}}})=\mathit{\boldsymbol{h}}( {\mathit{\boldsymbol{X}}}) \end{align} $ | (43) |
因此,0阶李导数的梯度即为观测方程的雅可比矩阵,表示为
| $ \begin{align} \nabla L^{0}\mathit{\boldsymbol{h}}({\mathit{\boldsymbol{X}}})& =\nabla \mathit{\boldsymbol{h}}( {\mathit{\boldsymbol{X}}}) \\ & =\begin{bmatrix} {\mathit{\boldsymbol{I}}_{3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 9}} \\ {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{I}}_{3}} & {\mathit{\boldsymbol{0}}_{3\times 9}} \\ {\mathit{\boldsymbol{a}}} & {-\mathit{\boldsymbol{a}}} & {\mathit{\boldsymbol{0}}_{1\times 3}} & {\mathit{\boldsymbol{0}}_{1\times 9}} \\ {\mathit{\boldsymbol{0}}_{1\times 3}} & {\mathit{\boldsymbol{b}}} & {-\mathit{\boldsymbol{b}}} & {\mathit{\boldsymbol{0}}_{1\times 9}} \end{bmatrix} \end{align} $ | (44) |
式中
| $ \begin{align} \mathit{\boldsymbol{a}}& =\frac{\mathit{\boldsymbol{r}}_{1} -\mathit{\boldsymbol{r}}_{2}} {l_{1}} \end{align} $ | (45) |
| $ \begin{align} \mathit{\boldsymbol{b}}& =\frac{\mathit{\boldsymbol{r}}_{2} -\mathit{\boldsymbol{r}}_{3}} {l_{2}} \end{align} $ | (46) |
2) 1阶李导数
| $ \begin{align} L_{\mathit{\boldsymbol{f}}_{0}}^{1} \mathit{\boldsymbol{h}}({\mathit{\boldsymbol{X}}}) =[{\mathit{\boldsymbol{\dot{r}}}_{1}} \; \; {\mathit{\boldsymbol{\dot{r}}}_{3}} \; \; {h_{1}} \; \; {h_{2}} ]^{\rm T} \end{align} $ | (47) |
式中
| $ \begin{align} & \nabla L_{\mathit{\boldsymbol{f}}_{0}}^{1} \mathit{\boldsymbol{h}}({\mathit{\boldsymbol{X}}}) \\ =& \begin{bmatrix} {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{I}}_{3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} \\ {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{I}}_{3}} \\ {\mathit{\boldsymbol{x}}_{1}} & {-\mathit{\boldsymbol{x}}_{1}} & {\mathit{\boldsymbol{0}}_{1\times 3}} & {\mathit{\boldsymbol{a}}} & {-\mathit{\boldsymbol{a}}} & {\mathit{\boldsymbol{0}}_{1\times 3}} \\ {\mathit{\boldsymbol{0}}_{1\times 3}} & {\mathit{\boldsymbol{x}}_{2}} & {-\mathit{\boldsymbol{x}}_{2}} & {\mathit{\boldsymbol{0}}_{1\times 3}} & {\mathit{\boldsymbol{b}}} & {-\mathit{\boldsymbol{b}}} \\ \end{bmatrix} \end{align} $ | (48) |
式中
3) 2阶李导数
| $ \begin{align} \nabla L_{\mathit{\boldsymbol{f}}_{1}}^{2} h_{7} ({\mathit{\boldsymbol{X}}}) =[{\mathit{\boldsymbol{c}}} \; \; {-\mathit{\boldsymbol{c}}} \; \; {\mathit{\boldsymbol{0}}_{1\times 3}} \; \; {\mathit{\boldsymbol{0}}_{1\times 3}} \; \; {\mathit{\boldsymbol{0}}_{1\times 3}} \; \; {\mathit{\boldsymbol{0}}_{1\times 3}} ] \end{align} $ | (49) |
式中
| $ \begin{align} c_{1} & =\frac{(r_{1, y} -r_{2, y})^{2}+(r_{1, z} -r_{2, z})^{2}}{m_{1} l_{1}^{3}} \end{align} $ | (50) |
| $ \begin{align} c_{2} & =-\frac{(r_{1, x} -r_{2, x})(r_{1, y} -r_{2, y})}{m_{1} l_{1}^{3}} \end{align} $ | (51) |
| $ \begin{align} c_{3} & =-\frac{(r_{1, x} -r_{2, x})(r_{1, z} -r_{2, z})}{m_{1} l_{1}^{3}} \end{align} $ | (52) |
| $ \begin{align} \nabla L_{\mathit{\boldsymbol{f}}_{2}}^{2} h_{7} ({\mathit{\boldsymbol{X}}}) & =[ {\mathit{\boldsymbol{d}}} \; \; {-\mathit{\boldsymbol{d}}} \; \; {\mathit{\boldsymbol{0}}_{1\times 3}} \; \; {\mathit{\boldsymbol{0}}_{1\times 3}} \; \; {\mathit{\boldsymbol{0}}_{1\times 3}} \; \; {\mathit{\boldsymbol{0}}_{1\times 3}} ] \end{align} $ | (53) |
式中
| $ \begin{align} d_{1} & =-\frac{(r_{1, x} -r_{2, x})(r_{1, y} -r_{2, y})}{m_{1} l_{1}^{3}} \end{align} $ | (54) |
| $ \begin{align} d_{2} & =\frac{(r_{1, x} -r_{2, x})^{2}+(r_{1, z} -r_{2, z})^{2}}{m_{1} l_{1}^{3}} \end{align} $ | (55) |
| $ \begin{align} d_{3} & =-\frac{(r_{1, y} -r_{2, y})(r_{1, z} -r_{2, z})}{m_{1} l_{1}^{3}} \end{align} $ | (56) |
将求得的李导数梯度合并,构造可观性矩阵
| $ \begin{align} \mathit{\boldsymbol{O}}_{3} =\begin{bmatrix} {\mathit{\boldsymbol{I}}_{3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} \\ {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{I}}_{3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} \\ {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{I}}_{3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} \\ {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{I}}_{3}} \\ {\mathit{\boldsymbol{\varXi}}_{1}} & {-\mathit{\boldsymbol{\varXi}}_{1}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} \\ {\mathit{\boldsymbol{X}}_{1}} & {-\mathit{\boldsymbol{X}}_{1}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{\varXi}}_{1}} & {-\mathit{\boldsymbol{\varXi}}_{1}} & {\mathit{\boldsymbol{0}}_{3\times 3}} \end{bmatrix} \end{align} $ | (57) |
式中
| $ \begin{align} \Im ({\bar{x}, \bar{y}, \bar{z}, m, l}) =\begin{bmatrix} {\dfrac{\bar{x}}{l}} & {\dfrac{\bar{y}}{l}} & {\dfrac{\bar{z}}{l}} \\[7pt] {\dfrac{\bar{y}^{2}+\bar{z}^{2}}{ml^{3}}} & {-\dfrac{\bar{x}\bar{y}}{ml^{3}}} & {-\dfrac{\bar{x}\bar{z}}{ml^{3}}} \\[7pt] {-\dfrac{\bar{x}\bar{y}}{ml^{3}}} & {\dfrac{\bar{x}^{2}+\bar{z}^{2}}{ml^{3}}} & {-\dfrac{\bar{y}\bar{z}}{ml^{3}}} \end{bmatrix} \end{align} $ | (58) |
可知,当
然后,假设当
最后,当
综上,非线性系统(16) 是可观的,证毕。
| $ \begin{align} & \mathit{\boldsymbol{\varXi}}_{1}' =\begin{bmatrix} {r_{1, x} -r_{2, x}} & {r_{1, y} -r_{2, y}} & {r_{1, z} -r_{2, z}} \\[-1pt] {({r_{1, x} -r_{2, x}})^{2}+({r_{1, y} -r_{2, y}})^{2}+({r_{1, z} -r_{2, z}})^{2}} & 0 & 0 \\[-1pt] 0 & {({r_{1, x} -r_{2, x}})^{2}+({r_{1, y} -r_{2, y}})^{2}+({r_{1, z} -r_{2, z}})^{2}} & 0 \end{bmatrix} \end{align} $ | (59) |
| $ \begin{align} & \mathit{\boldsymbol{O}}_{n} =\begin{bmatrix} {\mathit{\boldsymbol{I}}_{3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & \cdots & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & \cdots & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} \\[-1pt] {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & \cdots & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{I}}_{3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & \cdots & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} \\[-1pt] {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & \cdots & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{I}}_{3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & \cdots & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} \\[-1pt] {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & \cdots & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & \cdots & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{I}}_{3}} \\[-1pt] {\mathit{\boldsymbol{\varXi}}_{1}} & {-\mathit{\boldsymbol{\varXi}}_{1}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & \cdots & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & \cdots & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} \\[-1pt] {\mathit{\boldsymbol{X}}_{1}} & {-\mathit{\boldsymbol{X}}_{1}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & \cdots & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{\varXi}}_{1}} & {-\mathit{\boldsymbol{\varXi}}_{1}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & \cdots & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} \\[-1pt] \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots & \vdots \\[-1pt] {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & \cdots & {\mathit{\boldsymbol{\varXi}}_{n-1}} & {-\mathit{\boldsymbol{\varXi}}_{n-1}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & \cdots & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} \\[-1pt] {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & \cdots & {\mathit{\boldsymbol{X}}_{n-1}} & {-\mathit{\boldsymbol{X}}_{n-1}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & {\mathit{\boldsymbol{0}}_{3\times 3}} & \cdots & {\mathit{\boldsymbol{\varXi}}_{n-1}} & {-\mathit{\boldsymbol{\varXi}}_{n-1}} & {\mathit{\boldsymbol{0}}_{3\times 3}} \end{bmatrix} \end{align} $ | (60) |
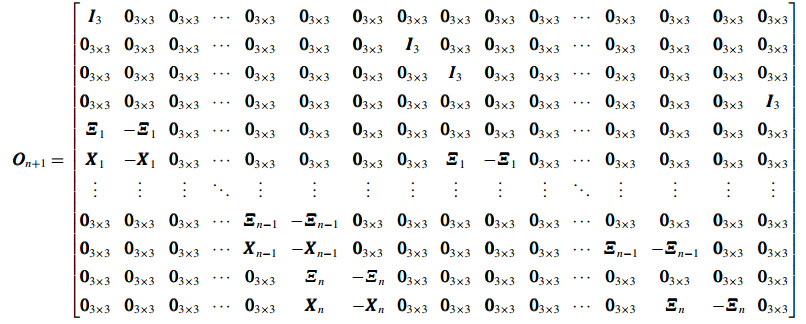
|
(61) |
为验证本文算法的有效性,本节给出当
|
|
表 1 初始参数和状态 Tab. 1 Initial state and parameters |
图 3和图 4为卫星1和卫星3滤波前后的误差对比图,为了方便观察,这里只画出了500 s内的滤波误差对比结果。图 5~图 7为卫星1在2个周期内在
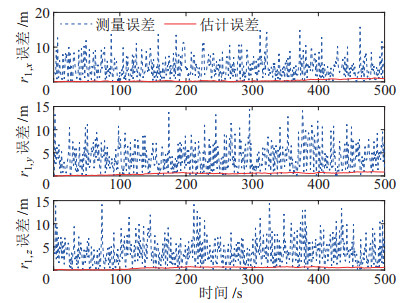
|
图 3 卫星1误差对比 Fig.3 Error comparison of satellite 1 |

|
图 4 卫星3误差对比 Fig.4 Error comparison of satellite 3 |
|
图 5 卫星1在X方向的位置估计结果 Fig.5 Position estimation result of satellite 1 in X direction |
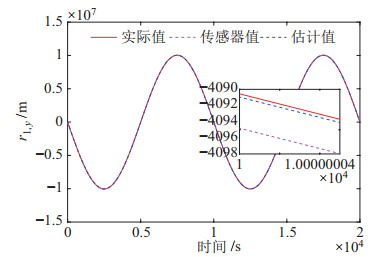
|
图 6 卫星1在Y方向的位置估计结果 Fig.6 Position estimation result of satellite 1 in Y direction |
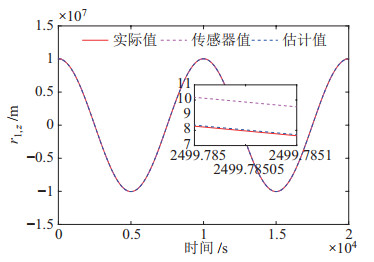
|
图 7 卫星1在Z方向的位置估计结果 Fig.7 Position estimation result of satellite 1 in Z direction |

|
图 8 卫星3在X方向的位置估计结果 Fig.8 Position estimation result of satellite 3 in X direction |
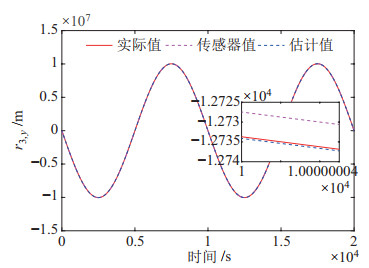
|
图 9 卫星3在Y方向的位置估计结果 Fig.9 Position estimation result of satellite 3 in Y direction |
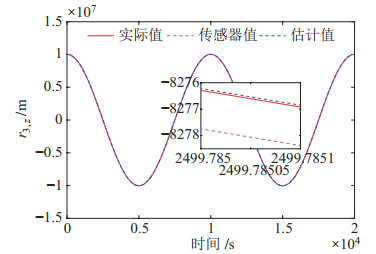
|
图 10 卫星3在Z方向的位置估计结果 Fig.10 Position estimation result of satellite 3 in Z direction |
为了定量地分析所提算法的滤波效果,表 2给出了2个运动周期内系统状态均方误差在滤波前后的统计数据,从表 2可以看出,滤波后系统状态的误差约减小了90{%} 以上。位置估计精度达到分米级别,特别是在
|
|
表 2 状态估计均方误差 Tab. 2 Mean square error of state estimation |
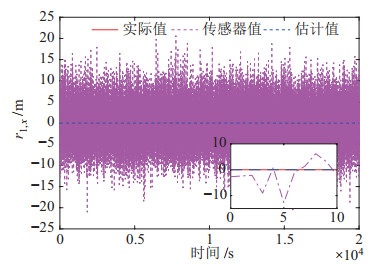
考虑到GPS传感器更新频率较低,难以满足航天器实时导航的需求,本文采用每预测
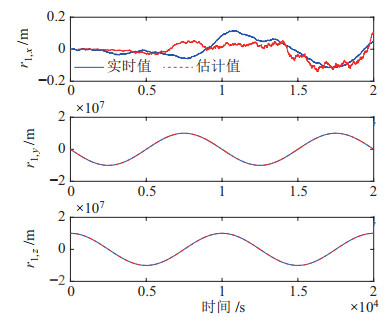
|
图 11 卫星1的实时跟踪结果 Fig.11 Real-time tracking result of satellite 1 |
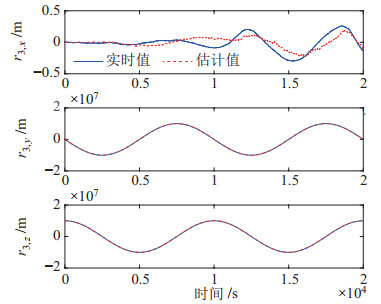
|
图 12 卫星3的实时跟踪结果 Fig.12 Real-time tracking result of satellite 3 |
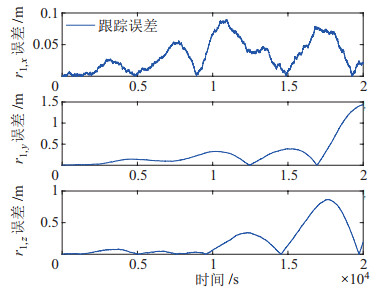
|
图 13 卫星1的实时跟踪误差 Fig.13 Real-time tracking error of satellite 1 |

|
图 14 卫星3的实时跟踪误差 Fig.14 Real-time tracking error of satellite 3 |
为考察卫星2的状态可观性,需要进一步开展仿真验证。图 15~图 17为卫星2在

|
图 15 卫星2在X方向的实时跟踪结果 Fig.15 Real-time tracking result of satellite 2 in X direction |
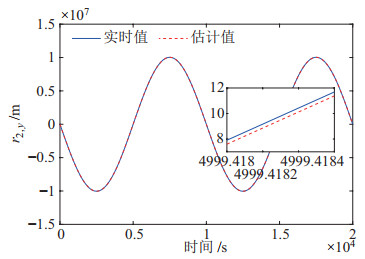
|
图 16 卫星2在Y方向的实时跟踪结果 Fig.16 Real-time tracking result of satellite 2 in Y direction |

|
图 17 卫星2在Z方向的实时跟踪结果 Fig.17 Real-time tracking result of satellite 2 in Z direction |
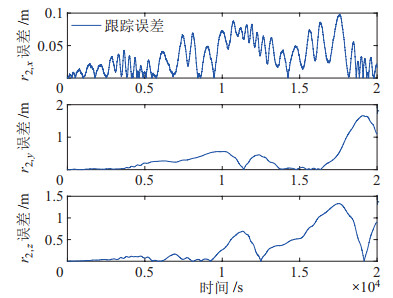
|
图 18 卫星2的实时跟踪误差 Fig.18 Real-time tracking error of satellite 2 |
综上可知,本文算法能够有效保证STS的状态估计精度和实时跟踪。并且在仅使用2个GPS传感器的条件下,
针对直链式
| [1] |
孟中杰, 黄攀峰, 鲁迎波, 等. 在轨服务中空间系绳的应用及发展[J]. 宇航学报, 2019, 40(10): 1134-1145. Meng Z J, Huang P F, Lu Y B, et al. Application and development of space tether in on-orbit servicing[J]. Journal of Astronautics, 2019, 40(10): 1134-1145. DOI:10.3873/j.issn.1000-1328.2019.10.004 |
| [2] |
Huang P F, Zhang F, Chen L, et al. A review of space tether in new applications[J]. Nonlinear Dynamics, 2018, 94: 1-19. DOI:10.1007/s11071-018-4389-5 |
| [3] |
Huang P F, Zhang F, Cai J, et al. Dexterous tethered space robot: Design, measurement, control, and experiment[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(3): 1452-1468. DOI:10.1109/TAES.2017.2671558 |
| [4] |
Chung S J, Slotine J J E, Miller D W. Nonlinear model reduction and decentralized control of tethered formation flight[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(2): 390-400. DOI:10.2514/1.21492 |
| [5] |
Yamagiwa Y, Nohmi M, Aoki Y, et al. Space experiments on basic technologies for a space elevator using microsatellites[J]. Acta Astronautica, 2017, 138: 570-578. DOI:10.1016/j.actaastro.2016.12.022 |
| [6] |
Wang B H, Meng Z J, Jia C, et al. Reel-based tension control of tethered space robots[J]. IEEE Transactions on Aerospace and Electronic Systems, 2020, 56(4): 3028-3043. DOI:10.1109/TAES.2019.2958156 |
| [7] |
Yu B S, Jin D P, Wen H. Analytical deployment control law for a flexible tethered satellite system[J]. Aerospace Science and Technology, 2017, 66: 294-303. DOI:10.1016/j.ast.2017.02.026 |
| [8] |
Ellis J R, Hall C D. Model development and code verification for simulation of electrodynamic tether system[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(6): 1713-1722. DOI:10.2514/1.44638 |
| [9] |
徐秀栋, 黄攀峰, 孟中杰. 空间绳系机器人抓捕目标过程协同稳定控制[J]. 机器人, 2014, 36(1): 100-110. Xu X D, Huang P F, Meng Z J. Coordinated stability control of tethered space robot for capturing the target[J]. Robot, 2014, 36(1): 100-110. |
| [10] |
Huang P F, Wang D K, Meng Z J, et al. Impact dynamic modeling and adaptive target capturing control for tethered space robots with uncertainties[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(5): 2260-2271. DOI:10.1109/TMECH.2016.2569466 |
| [11] |
Zhang Y Z, Huang P F, Song K H, et al. An angles-only navigation and control scheme for noncooperative rendezvous operations[J]. IEEE Transactions on Industrial Electronics, 2019, 66(11): 8618-8627. DOI:10.1109/TIE.2018.2884213 |
| [12] |
Ma Z Q, Huang P F. Nonlinear analysis of discrete-time sliding mode prediction deployment of tethered space robot[J]. IEEE Transactions on Industrial Electronics, 2021, 68(6): 5166-5175. DOI:10.1109/TIE.2020.2992006 |
| [13] |
Yousefian P, Salarieh H. Nonlinear control of sway in a tethered satellite system via attitude control of the main satellite[J]. Aerospace Science and Technology, 2017, 63: 317-327. DOI:10.1016/j.ast.2016.12.023 |
| [14] |
Chung S J, Kong E, Miller D. Dynamics and control of tethered formation flight spacecraft using the SPHERES testbed[C] //AIAA Guidance, Navigation, and Control Conference and Exhibit. Reston, USA: AIAA, 2005. DOI: 10.2514/6.2005-6089.
|
| [15] |
Misra A K, Amier Z, Modi V J. Attitude dynamics of three-body tethered systems[J]. Acta Astronautica, 1988, 17(10): 1059-1068. DOI:10.1016/0094-5765(88)90189-0 |
| [16] |
Li G Q, Zhu Z H. On libration suppression of partial space elevator with a moving climber[J]. Nonlinear Dynamics, 2019, 97(4): 2107-2125. DOI:10.1007/s11071-019-05108-0 |
| [17] |
Shi G F, Zhu Z X, Zhu Z H, et al. Parallel optimization of trajectory planning and tracking for three-body tethered space system[J]. IEEE/ASME Transactions on Mechatronics, 2019, 24(1): 240-247. DOI:10.1109/TMECH.2019.2890900 |
| [18] |
Wang Z K, Cui N G, Fan Y H, et al. Modal and dynamic analysis of a tether for a nonequatorial space elevator[J]. IEEE Access, 2018, 6: 74940-74952. DOI:10.1109/ACCESS.2018.2883363 |
| [19] |
Netzer E, Kane T R. Estimation and control of tethered satellite systems[J]. Journal of Guidance, Control, and Dynamics, 1995, 18(4): 851-858. DOI:10.2514/3.21469 |
| [20] |
Fang G T, Zhang Y Z, Huang P F, et al. State estimation of double-pyramid tethered satellite formations using only two GPS sensors[J]. Acta Astronautica, 2021, 180: 507-515. DOI:10.1016/j.actaastro.2020.12.043 |
| [21] |
Macdonald M, Badescu V. The international handbook of space technology[M]. Berlin, Germany: Springer, 2014.
|
| [22] |
Kojima H, Iwasaki M, Fujii H A. Nonlinear control of librational motion of tethered satellites in elliptic orbits[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(2): 229-239. DOI:10.2514/1.9166 |
| [23] |
Kumar K D. Review on dynamics and control of nonelectrodynamic tethered satellite systems[J]. Journal of Spacecraft and Rockets, 2006, 43(4): 705-720. DOI:10.2514/1.5479 |
| [24] |
Zhou G J, Li K Y, Kirubarajan T, et al. State estimation with trajectory shape constraints using pseudomeasurements[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(5): 2395-2407. DOI:10.1109/TAES.2018.2887180 |
| [25] |
Xu L F, Li X R, Duan Z S, et al. Modeling and state estimation for dynamic systems with linear equality constraints[J]. IEEE Transactions on Signal Processing, 2013, 61(11): 2927-2939. DOI:10.1109/TSP.2013.2255045 |
| [26] |
Simon D. Kalman filtering with state constraints: A survey of linear and nonlinear algorithms[J]. IET Control Theory & Applications, 2010, 4(8): 1303-1318. |
| [27] |
Xu L F, Li X R, Liang Y, et al. Constrained dynamic systems: Generalized modeling and state estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(5): 2594-2609. DOI:10.1109/TAES.2017.2705518 |
| [28] |
Liu C J, Li B B, Chen W H. Particle filtering with soft state constraints for target tracking[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(6): 3492-3504. DOI:10.1109/TAES.2019.2908292 |
| [29] |
Cho H, Udwadia F E. Explicit control force and torque determination for satellite formation-keeping with attitude requirements[J]. Journal of Guidance, Control, and Dynamics, 2013, 36(2): 589-605. DOI:10.2514/1.55873 |
| [30] |
Liu Y, Zhang F, Huang P F, et al. Analysis, planning and control for cooperative transportation of tethered multi-rotor UAVs[J]. Aerospace Science and Technology, 2021, 113. DOI:10.1016/j.ast.2021.106673 |
| [31] |
Udwadia F E, Kalaba R E. Analytical dynamics: A new approach[M]. Cambridge, UK: Cambridge University Press, 1996.
|
| [32] |
Qi J J, Sun K, Wang J H, et al. Dynamic state estimation for multi-machine power system by unscented Kalman filter with enhanced numerical stability[J]. IEEE Transactions on Smart Grid, 2018, 9(2): 1184-1196. DOI:10.1109/TSG.2016.2580584 |
| [33] |
Menegaz H M T, Ishihara J Y, Borges G A, et al. A systematization of the unscented Kalman filter theory[J]. IEEE Transactions on Automatic Control, 2015, 60(10): 2583-2598. DOI:10.1109/TAC.2015.2404511 |
| [34] |
Wolfe J D, Speyer J L, Lee E, et al. Estimation of relative satellite position using transformed differential carrier-phase GPS measurements[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(5): 1217-1227. DOI:10.2514/1.11691 |
| [35] |
Gong B C, Wang S, Hao M R, et al. Range-based collaborative relative navigation for multiple unmanned aerial vehicles using consensus extended Kalman filter[J]. Aerospace Science and Technology, 2021, 112. DOI:10.1016/j.ast.2021.106647 |
| [36] |
Zhang Y Z, Song K H, Yi J G, et al. Absolute attitude estimation of rigid body on moving platform using only two gyroscopes and relative measurements[J]. IEEE/ASME Transactions on Mechatronics, 2018, 23(3): 1350-1361. DOI:10.1109/TMECH.2018.2811730 |
 2022, Vol. 44
2022, Vol. 44


