1 引言（Introduction）

空间在轨服务一直是空间技术中一项重要的研究课题^[1]。空间机械臂被认为是取代人类宇航员执行危险、困难太空任务的重要手段，可以执行的操作任务包括目标检测、抓取、安装、拆卸等^[2]。而复杂的空间环境为空间机械臂的设计和开发带来了巨大的挑战。

模块化机械臂是提高机械臂系统耐用性和降低设计成本的有效解决方案^[3]。目前的蛇形机器人具有很好的模块性，并且已在地面和水下得到了成功应用^[4-6]。对于空间机械臂而言，机械臂关节发生故障将严重影响机械臂的性能，而且在复杂的太空环境中对空间机械臂进行维修需要付出极大的人力、物力成本。模块化的超冗余机械臂是解决这一问题的有效途径，通过直接更换发生故障的机械臂模块能减少航天员的出舱时间、降低操作难度。同时，超冗余机械臂具有很高的灵活度和避障能力，即其中某一关节发生故障，也不会对机械臂的性能造成很大影响。因此，开发模块化的超冗余空间机械臂是未来空间机械臂的重要发展方向。

自加拿大在1981年开发了世界上第一个用于执行在轨空间任务的机械臂系统SRMS后^[7]，在接下来的几十年间，各国相继开发了许多用于执行在轨任务的空间机械臂。例如空间站遥控操纵器系统^[8]、加拿大航天局研发的专用灵巧机械臂SPDM^[9]、日本研制的实验舱遥操作机械臂系统^[10]以及用于国际空间站的欧洲机械臂^[11]。为了搭建和维护空间站，我国研制了中国空间站远程机械臂系统CSSRMS，主要包括2个7自由度的核心舱机械臂和实验舱机械臂^[12]。上述冗余空间机械臂可以完成一般的搬运、维修等避障运动，其主要适用场景是航天舱外的较大工作空间，所以其臂杆较长，但是较长的臂杆会导致机械臂小范围的避障运动受到极大的限制，而且机械臂的冗余自由度较少，灵活性不足。加拿大研发的灵巧机械臂SPDM采用双臂结构，提高了机械臂系统的灵活度，但是单臂的自由度数目都没有超过7个，仍然难以在小范围复杂环境中工作。日本提出的空间机械臂是将一大一小2只具有6个自由度的机械臂串联在一起，总自由度达到12，但是在小范围环境中工作的主要是6自由度小臂，其避障能力有限。此外，其他仍处于地面实验阶段的空间机械臂包括德国轨道服务任务机械臂DEOS（deutsche orbit servicing mission，DEOS）^[13]、凤凰计划机械臂^[14]、Lemur IIb机械臂^[15]等，这些都没有真正实现模块化，因此在关节发生故障后很难进行更换。

从以上研究可以看出，目前采用模块化关节的超冗余机械臂仍没有被应用到空间机械臂的设计中。超冗余机械臂的优点是运动灵活度高、避障能力强，但是自由度的增加也会给机械臂的制造和控制带来困难，因为增加自由度会使累积误差增大，导致机械臂的运动精度和运动稳定性降低。一般而言，超冗余机械臂可以分为连续型机械臂和关节型机械臂。连续型机械臂常使用柔性可伸长的软材料作为机械臂本体，如中国科学技术大学Jiang等^[16]提出了一种蜂巢气动网络结构，并基于这种结构制备了兼具灵活度和大负载能力的软体机械臂，可以完成开门和拉抽屉等复杂任务。上海交通大学谷国迎团队^[17-18]设计的线缆驱动的超冗余机械臂具有24个自由度，可以灵活地跨越复杂的障碍环境。大连理工大学彭海军团队^[19]利用张拉整体结构质量轻、变形大等特点，提出一种基于张拉整体结构的连续型机械臂。但连续型的超冗余机械臂往往不具备大的负载能力，并且很难达到较高的控制精度。关节型机械臂是由多个刚性机械臂关节串联组成，如Transeth等^[20-21]和Wright等^[22]模仿蛇跨越障碍时的步态设计了一种蛇形机器人，它具有很高的灵活性与适应性，并且能够在复杂的地形中执行搜救任务。Mu等^[23]设计了2种模块化、球形关节的蛇形机器人，降低了机器人移动时与道路之间的摩擦。上述冗余的蛇形机器人往往被用于探索复杂的地面环境，不具备抓取或移动重物的能力。Gallardo等^[24]设计了一种由并联机构模块组成的机械关节的超冗余机械臂，利用旋量理论进行了运动学分析，并通过实验证明了该机器人良好的运动性能。Zhao等^[25-26]设计了一种由并联机构模块组成的超冗余机械臂，与之结构相似的还有Hu等^[27-28]设计的由并联模块组成的超冗余机械臂。Taherifar等^[29]提出了一种由液压系统驱动的并联模块组成的超冗余机械臂，通过液压阀控制机械臂的运动，具有高刚度和强负载能力的优点。这种由并联模块组成的机械臂往往有较高的定位精度，但控制复杂，并且机械臂体积较大，并不适于执行空间在轨组装或在轨服务任务。Xu等^[30]设计了一个9自由度的超冗余机械臂，但该机械臂仅由多个电机串联组装，机械臂线缆均暴露在外，并且机械臂的末端负载很小。

综上所述，现有的超冗余机械臂仍存在末端负载小、体积大等问题，难以满足在轨组装的任务需求。为了解决上述问题，本文设计了一种可用于在轨服务的模块化超冗余空间机械臂，如图 1所示。所设计的空间机械臂采用模块化设计，由9个关节模块串联构成，具有良好的灵活性与容错性。机械臂关节模块设计紧凑，电子元件被集成在内部的电路板中。为了实现机械臂在复杂环境中的灵活操作，分别推导了机械臂的正运动学和逆运动学模型，通过机械臂的避障实验验证了其通过复杂障碍环境的灵活性。为了增强机械臂的力感知能力设计了阻抗控制器，并分别进行了写字实验、恒力控制实验以及机械臂的协同搬运实验。

2 机械结构设计（Mechanical structure design）

模块化超冗余空间机械臂通过9个相同的接头与集成控制系统连接，每个关节包括机械系统和电子控制系统，具有高集成、低重量和大负载的优点。机械臂的模型图和实物图如图 2所示，相邻关节之间沿关节中心轴线以90$ ^{\circ} $夹角连接，各连接板均进行了减质量处理以降低机械臂整体的质量。所设计的机械臂系统参数如表 1所示。

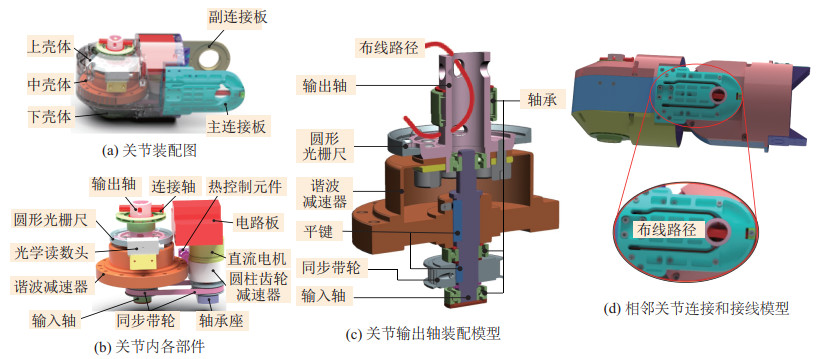
所设计的机械臂关节如图 3所示，其中，图 3(a)表示关节的壳体结构和连接件结构。可以看出，关节的外部结构主要包括上壳体、中壳体和下壳体，各壳体之间通过螺栓连接。图 3(b)表示关节内部各结构的排布情况，左侧包括关节的输出轴和连接轴，圆形光栅尺和光学读数头用于测量关节的旋转角度，谐波减速器被固定在中部壳体。直流电机通过同步带轮将动力传递到谐波减速器，其直流电机的末端安装有圆柱齿轮减速器，驱动器等电子器件被固定在电机上部。底壳内的轴承支架等部件主要用于辅助电机轴旋转。关节采用Maxon永磁同步电机提供驱动力，该电机具有散热性好、使用寿命长和瞬时转矩过载能力强等优点。

机械臂关节采用了2级减速设计来增大关节的输出扭矩，分别为安装在电机输出轴上的Maxon行星齿轮减速器和固定在输出轴的Nidec Shimpo谐波减速器，总减速比达$ 3120:1 $，这使得机械臂关节最大可提供190 N$ \cdot $m的输出扭矩^[31]。电机将产生的扭矩直接传递给直齿圆柱齿轮减速器，从而使齿轮轴产生扭矩，进而通过同步带轮将扭矩传递给输入轴，再通过谐波减速器放大输入轴的扭矩，并将其传递到输出轴。最后，输出轴通过连接轴将上一个关节的输出扭矩传递给下一个关节，从而达到关节旋转的目的，其关节输出轴组件模型如图 3(c)所示。

机械臂关节之间的布线也是关节的设计难点之一，所设计的关节可以将相邻2个关节之间的连接线内嵌于关节的副连接板中，如图 3(d)所示。副连接板外部安装主连接板，避免机械臂线路的外露和线路缠绕。机械臂仅需一根通信总线和电源线即可连接到机械臂的各个关节，其中通信总线和电源线分别布置在关节两侧的连接板中。

关节内的传感器由3部分组成。第一部分为增量式编码器，与电机直接相连，用于测量电机的转速；第二部分是集成在控制器内部的电流传感器，为电机提供电流闭环控制和限流保护；第三部分是圆形光栅尺读数头，连接在关节输出轴上，读数头通过BiSS（双工同步串行）通信读取圆形光栅尺的刻度，实时检测输出轴的角度值，精度可达$ 6.86\times 10^{-4} $($ ^\circ $)。读数头记录的数据被传递给控制器，以校正关节实际输出的角度偏差。

为了降低样机在地面测试时的成本，接头壳体材料选用7A09型号的硬质合金，而不是昂贵的碳纤维。受地面重力的影响，连接轴和输出轴由TC4型号的钛合金改为40Cr型号的合金。同时，接头外壳表面进行阳极氧化和喷砂处理，以防止磨损和腐蚀。

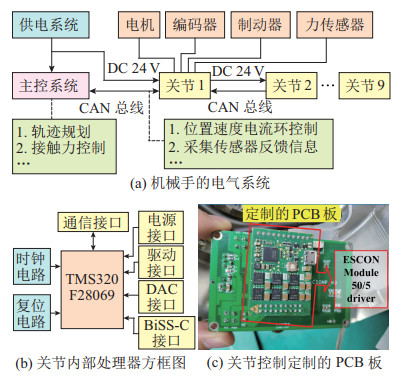
3 电控方案设计（Design of the electrical control scheme）

超冗余机械臂的电控系统由一个供电系统、一个主控系统以及各关节内部的电气系统组成，如图 4(a)所示。为了提高控制系统的可靠性和计算能力，采用TMS320F28069浮点处理器作为控制器，实现控制器局域网络（controller area network，CAN）总线通信、传感器信息采集和位置控制，如图 4(b)所示。图 4(c)表示每个关节内部定制的PCB（printed circuit board）板，包括与Maxon电机相匹配的ESCON模块50/5驱动器、霍尔传感器接口和增量式编码器接口。

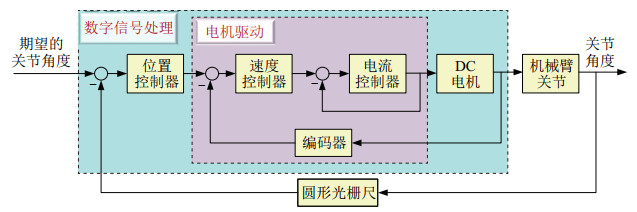
图 5为机械臂的位置、速度以及电流的三路回环控制框图。电流回路控制器位于最内环，由于需要保护控制电路，必须限制电流回路的输入和输出，以避免电流过载造成电机损坏。速度环在电流环之外，控制伺服系统的速度。为了避免传动系统中间隙、摩擦等非线性因素的影响，速度控制采用了以电机转速为被控对象的内闭环。位置环在速度环之外，为保证控制精度满足要求，位置环采用外闭环控制输出轴的角度。

机械臂的系统通信由2部分组成，一部分是单关节通过串行外设接口进行内部通信，另一部分是单关节与主控单元通过控制器CAN总线进行通信。串行外设接口通信主要用于采集圆形光栅尺上的信息，并向数模转换模块发送指令，实现对单关节的位置控制。CAN总线通信允许机械臂的主控系统获得每个关节的状态信息，然后作出相应的决定。

为了方便操作人员对所设计的机械臂进行运动控制，针对所设计的机械臂开发了一套控制软件，其软件框架如图 6所示。机械臂上位机软件可以提供良好的人机操作界面和丰富的接口，并能够实时显示机械臂信息。下位机软件接收并处理来自上位机、传感器和关节驱动器的控制指令和传感器数据，实现对机械臂精准、灵活的控制。

4 机械臂运动学与阻抗控制方法（Kinema- tics and impedance control method of the manipulator） 4.1 机械臂的正运动学

建立机械臂的正、逆运动学方程是机械臂进行路径规划的基础。在图 7中，将机械臂的各关节简化为连杆，并在各关节的连接处建立坐标系。表 2中，使用改进的DH（modified Denavit-Hartenberg，MDH）参数法建立机械臂的运动学模型，其中$ \alpha_{i-1} $表示两相邻关节之间的关节角，$ a_{i-1} $表示两相邻旋转轴之间的距离，$ d_{i-1} $表示关节轴线从一个连杆坐标系到另一个连杆坐标系的距离，$ \theta_{i-1} $表示一个连杆相对于另一个连杆的关节轴线的旋转角度，$ i=1, 2, \cdots, 9 $。

因此可以推导出连杆$ i $相对于连杆$ i-1 $的位置关系的变换矩阵$ {}^{i-1}_{\; \; \; i}{{\mathit{\boldsymbol{T}}}} $：

$ \begin{align} {}_{\; \; \; i}^{i-1}{{\mathit{\boldsymbol{T}}}}=&{\rm rot}\left(X_{i-1}, \alpha_{i-1}\right) {\rm trans}\left(a_{i-1}, 0, 0\right){\rm rot}\left(Z_{i}, \theta_{i}\right) \times \\ &{\rm trans}\left(0, 0, d_{i}\right) \\ =&\! \begin{bmatrix} 1 \!& 0 \!& 0\! & 0 \\ 0 \!& {\rm c} \alpha_{i-1}\! & -{\rm s} \alpha_{1-1} \!& 0 \\ 0 \!& {\rm s} \alpha_{i-1} \!& {\rm c} \alpha_{1-1} \!& 0 \\ 0 \!& 0 \!& 0 \!& 1 \end{bmatrix} \!\!\times\!\! \begin{bmatrix} 1\! & 0 \!& 0\! & a_{i-1} \\ 0 \!& 1 \!& 0 \!& 0 \\ 0 \!& 0 \!& 1 \!& 0 \\ 0 \!& 0 \!& 0 \!& 1 \end{bmatrix} \!\!\times\!\! \\ & \begin{bmatrix} {\rm c} \theta_{i} & -{\rm s} \theta_{i} & 0 & 0 \\ {\rm s} e_{i} & {\rm c} \theta_{i} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \times \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & d_{i} \\ 0 & 0 & 0 & 1 \end{bmatrix} \\ =& \begin{bmatrix} {\rm c} \theta_{i} \!&\! -{\rm s} \theta_{i} \!&\! 0 \!&\! a_{i-1} \\ {\rm s} \theta_{i} {\rm c} \alpha_{i-1} \!&\! {\rm c} \theta_{i} {\rm c} \alpha_{i-1}\! &\! -{\rm s} \alpha_{i-1} \!&\! -{\rm s} \alpha_{i-1} d_{i} \\ {\rm s} \theta_{i} {\rm s} \alpha_{i-1} \!&\! {\rm c} \theta_{i} {\rm c} \alpha_{i-1} \!& {\rm c} \alpha_{i-1} \!&\! {\rm c} \alpha_{i-1} d_{i} \\ 0 \!&\! 0 \!&\! 0 \!& \!1 \end{bmatrix} \end{align} $

(1)

其中$ {\rm c}\theta =\cos \theta $，$ {\rm s}\theta =\sin \theta $，$ {\rm c}\alpha_{i-1} =\cos \alpha_{i-1} $，$ {\rm s}\alpha_{i-1} $ $ = $ $ \sin \alpha_{i-1} $。根据式(1) 可以得到，机械臂末端坐标系相对于基坐标系的位姿矩阵$ {}_{9}^{0} {{\mathit{\boldsymbol{T}}}} $与关节变量向量$ \mathit{\boldsymbol{\varTheta}}=[\theta_{1}, \cdots, \theta_{9}]^{\rm T} $的函数$ {{\mathit{\boldsymbol{f}}}}_{\rm kine}(\mathit{\boldsymbol{\varTheta}}) $为

$ \begin{align} {}_{9}^{0} {{\mathit{\boldsymbol{T}}}} &={{\mathit{\boldsymbol{f}}}}_{\rm kine}(\mathit{\boldsymbol{\varTheta}}) \\ &={}_{1}^{0} {{\mathit{\boldsymbol{T}}}}_{2}^{1} {{\mathit{\boldsymbol{T}}}}_{3}^{2} {{\mathit{\boldsymbol{T}}}}_{4}^{3} {{\mathit{\boldsymbol{T}}}}_{5}^{4} {{\mathit{\boldsymbol{T}}}}_{6}^{5}{{\mathit{\boldsymbol{T}}}}_{7}^{6} {{\mathit{\boldsymbol{T}}}}_{8}^{7} {{\mathit{\boldsymbol{T}}}}_{9}^{8} {{\mathit{\boldsymbol{T}}}} \\ &=\begin{bmatrix} r_{11} & r_{12} & r_{13} & P_{x} \\ r_{21} & r_{22} & r_{23} & P_{y} \\ r_{31} & r_{32} & r_{33} & P_{z} \\ 0 & 0 & 0 & 1 \end{bmatrix} \end{align} $

(2)

式(2) 给出了末端执行器相对于基础坐标系的位置和姿态，可以用矩阵$ \mathit{\boldsymbol{X}}= \begin{bmatrix} r_{11} & r_{12} & r_{13} \\ r_{21} & r_{22} & r_{23} \\ r_{31} & r_{32} & r_{33}\\ \end{bmatrix} $表示机械臂末端的姿态，$ \mathit{\boldsymbol{P}}=[P_{x}\; \; P_{y}\; \; P_{z}] $表示机械臂末端的位置，以上描述了9自由度机械臂的正向运动学。

4.2 机械臂的逆运动学

机械臂的逆运动学解算即通过已知机器人的末端位姿$ {}_{9}^{0}\mathit{\boldsymbol{T}} $对相应的关节变量进行求解的过程。梯度投影法将逆运动学问题的解分解为最小范数解和齐次解2部分，第1项称为特解，能完成机械臂的运动，第2项称为齐次解，对机械臂末端在笛卡儿空间的速度矢量没有影响。通过求解正向运动学关于时间的导数，可以得到机械臂末端的速度与关节角度之间的关系为

$ \begin{align} \dot{\mathit{\boldsymbol{x}}}_{i}= \begin{bmatrix} v_{i} \\ \omega_{i}\\ \end{bmatrix} =\mathit{\boldsymbol{J}}(\mathit{\boldsymbol{\varTheta}}) \dot{\mathit{\boldsymbol{\varTheta}}} \end{align} $

(3)

其中，$ \mathit{\boldsymbol{J}}(\mathit{\boldsymbol{\varTheta}}) $是关于$ \mathit{\boldsymbol{\varTheta}} $的雅可比矩阵，它建立了机械臂关节角和末端速度之间的关系。根据式(3) 可以得到，当$ \mathit{\boldsymbol{J}}(\mathit{\boldsymbol{\varTheta}}) $满秩时，机械臂的关节角速度可以表示为

$ \begin{align} \dot{\mathit{\boldsymbol{\varTheta}}}=\mathit{\boldsymbol{J}}^{-1}(\mathit{\boldsymbol{\varTheta}}) \begin{bmatrix} v_{i} \\ \omega_{i}\\ \end{bmatrix} \end{align} $

(4)

由于本文所设计的机械臂为超冗余的，因此无论是否满秩，该矩阵都无法得到常规的逆。目前绝大多数对冗余自由度机器人的研究都使用伪逆法求解，其计算如下：

$ \begin{align} \dot{\mathit{\boldsymbol{\varTheta}}}=\mathit{\boldsymbol{J}}^{+1}(\mathit{\boldsymbol{\varTheta}}) \begin{bmatrix} v_{i} \\ \omega_{i}\\ \end{bmatrix} \end{align} $

(5)

其中，$ \mathit{\boldsymbol{J}}^{+1}(\mathit{\boldsymbol{\varTheta}}) $表示雅可比矩阵$ \mathit{\boldsymbol{J}}(\mathit{\boldsymbol{\varTheta}}) $的伪逆矩阵。为防止出现奇异，引入阻尼系数$ u $，可以得到奇异鲁棒性逆矩阵：

$ \begin{align} \mathit{\boldsymbol{J}}^{\ast}=\mathit{\boldsymbol{J}}^{\mathrm{T}}\left(\mathit{\boldsymbol{J}}^{\mathrm{T}} \mathit{\boldsymbol{J}}+u^{2} \mathit{\boldsymbol{I}}\right)^{-1} \end{align} $

(6)

对于所设计的超冗余机械臂，式(5) 中的解为最小范数解，即所解出的机械臂关节角速度组成的向量范数最小。

为了在不改变机械臂末端位姿的情况下实现自运动，在式(4) 中增加齐次线性解，该齐次线性解与最小范数解是正交的关系，同时该解也包括在矩阵$ \mathit{\boldsymbol{J}} $的零空间内。此外，引入目标函数$ H(\bm\varTheta) $实现关节限位

$ \begin{align} H &=\dfrac{1}{9} \sum\limits_{i=1}^{9}\left(\dfrac{q_{i}-\dfrac{q_{i \max}+q_{i \min }}{2}}{\dfrac{q_{i \max}+q_{i \min }}{2}-q_{i \min }}\right)^{2} \\ &=\dfrac{1}{9} \sum\limits_{i=1}^{9}\left(\dfrac{q_{i}}{q_{i \max}}\right)^{2} \end{align} $

(7)

最后采用梯度投影法进行逆运动学的求解，解得：

$ \begin{align} \dot{\mathit{\boldsymbol{q}}}=\mathit{\boldsymbol{J}}^{+} \begin{bmatrix} v_{i} \\ \omega_{i} \end{bmatrix} + \mathit{\boldsymbol{k}}\left(\mathit{\boldsymbol{I}}-\mathit{\boldsymbol{J}}^{+} \mathit{\boldsymbol{J}}\right) \nabla H(\mathit{\boldsymbol{\varTheta}}) \end{align} $

(8)

其中，$ \mathit{\boldsymbol{I}} $为$ 9\times9 $的单位矩阵，$ \mathit{\boldsymbol{I}}-\mathit{\boldsymbol{J}}^{+} \mathit{\boldsymbol{J}} $是关于$ \mathit{\boldsymbol{J}} $的零空间投影矩阵，$ \mathit{\boldsymbol{k}} $为比例因子，$ \nabla H(\mathit{\boldsymbol{\varTheta}}) $可以表示为

$ \begin{align*} \nabla H(\mathit{\boldsymbol{\varTheta}})=\left[\frac{\partial H}{\partial \theta_{1}}, \frac{\partial H}{\partial \theta_{2}}, \cdots, \frac{\partial H}{\partial \theta_{9}}\right]^{\mathrm{T}} \end{align*} $

其中，比例因子$ {{\mathit{\boldsymbol{k}}}} $可设为

$ \begin{align*} {{\mathit{\boldsymbol{k}}}}={\rm diag}\; [0.0001\; \; 0.0001\; \; 0.0001\; \; 1\; \; 1\; \; 1] \end{align*} $

4.3 改进的Bi-RRT算法

为了使机械臂具备在复杂障碍环境中工作的能力，采用一种改进的基于双向快速搜索随机树（Bi-RRT）的轨迹规划算法。相较于传统的Bi-RRT算法，改进的Bi-RRT算法在创建搜索树之前先保存一棵完整的树，从而保留了一条完整的无障碍路径。这样，在计算从起点到目标点的无碰撞路径时，可以大大减少算法循环的次数，从而提高避障效率。

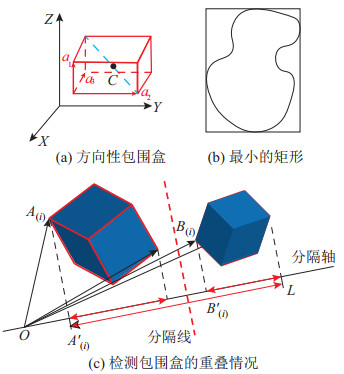
本文使用定向包围盒（OBB）算法来检测机械手与障碍物之间是否存在碰撞^[32]。OBB被定义为3维空间中任意方向的长方体。OBB边界框的模型如图 8(a)所示，其中$ C $表示边界框的中心，$ a_{1} $、$ a_{2} $和$ a_{3} $是方向轴。OBB的边界框是指包含对象和边框的最小矩形，如图 8(b)所示。图 8(c)表示利用包围盒进行碰撞检测，其中$ L $表示OBB的潜在分隔轴，$ O $为分隔轴上的一个随机点，$ A_{(i)} $和$ B_{(i)} $（$ i=1, 2, \cdots, 8 $）分别表示2个边界框上的端点。

$ \begin{align} O A_{(i)_{\max / \min }^{\prime}}&=\frac{\overrightarrow{O A_{(i)}} \cdot \overrightarrow{O L}}{|\overrightarrow{O L}|} \end{align} $

(9)

$ \begin{align} O B_{(i)_{\max / \min }^{\prime}}&=\frac{\overrightarrow{O B_{(i)}} \cdot \overrightarrow{O L}}{|\overrightarrow{O L}|} \end{align} $

(10)

$ \begin{align} \left|\overrightarrow{O B_{(i)}^{\prime}}\right|_{\max / \min }&=\frac{\overrightarrow{O B_{(i)}^{\prime}} \cdot \overrightarrow{O L}}{|\overrightarrow{O L}|} \end{align} $

(11)

2个边界框不重叠的充要条件是

$ \begin{align} \left|\overrightarrow{A_{(i)_{\min }^{\prime}} A_{(i)_{\max}}^{\prime}{ }}\right|+\left|\overrightarrow{B_{(i)_{\min }^{\prime}} B_{(i)_{\max}}^{\prime}{ }}\right|<\left|\overrightarrow{A_{(i)}^{\prime} B_{(i)}^{\prime}}\right|_{\max} \end{align} $

(12)

图 8(c)中的2个OBB有15个潜在的分隔轴，其中2个轴是2个长方体的方向轴，9个是方向轴的叉积。将OBB的边界框投影到$ L $轴上，并检查投影线段是否重合，如果投影线段没有发生重合，就可以认为机械臂没有与环境发生碰撞。

5 实验验证（Experimental verification）

为了说明所设计的机械臂穿越复杂障碍环境的能力与力控制能力，共开展了机械臂的避障实验、写字实验和力保持实验。

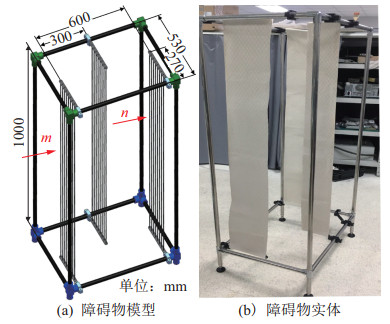
5.1 机械臂避障实验

高度的灵活性与避障能力是超冗余机械臂的重要优势，因此，为了验证所设计机械臂的灵活性，设计了一个复杂的障碍环境，主要包括3个挡板围起来的狭窄空间，如图 9所示。其中，障碍物尺寸为600 mm$ \times $530 mm$ \times $1000 mm，机械臂末端需要沿障碍物$ m $方向处进入障碍物，沿$ n $方向穿越障碍物。

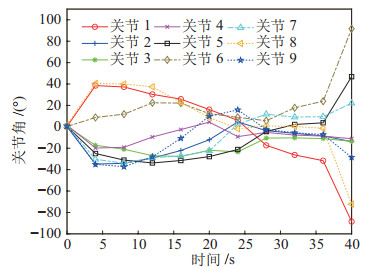
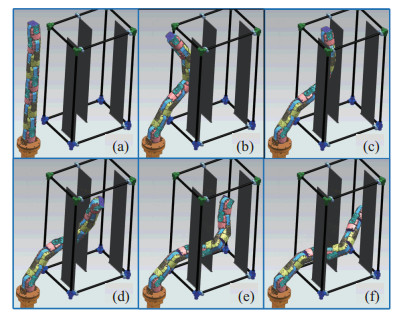
首先利用改进的Bi-RRT算法对机械臂在障碍环境中工作的过程进行仿真，仿真结果如图 10和图 11所示。由图 10可知，机械臂需要经过10次连续的关节角度变换才能穿越所设置的障碍环境。ADAMS软件仿真过程如图 11所示，可以看出，机械臂在穿越障碍的过程中没有与环境发生碰撞。

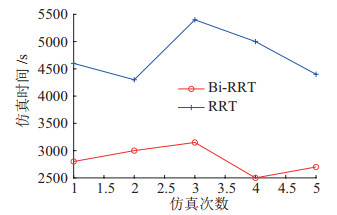
为了说明所采用的避障算法的优越性，分别使用改进的Bi-RRT算法和传统的Bi-RRT算法对所设计的机械臂进行了5次重复的穿越障碍环境的仿真实验，仿真结果如图 12所示。在仿真过程中，计算机采用了Intel$ ^\circledR $ Core$ ^\rm{TM} $ i7-7700中央处理器，运行频率为3.60 GHz，内存为8 GB，软件为Matlab R2017b，操作系统为Windows 10。图 12的计算结果表明，改进的Bi-RRT算法具有较短的计算时间和较高的效率。

将仿真得到的各阶段的关节角度下发给机械臂的各个关节控制机械臂穿越所设置的障碍环境。实验过程如图 13所示，可以看出，所设计的超冗余机械臂可以灵活地穿越复杂且狭窄的障碍环境，在穿越过程中没有与障碍物发生碰撞，并且机械臂关节穿越障碍环境的路径与仿真得到的路径几乎一致。采集的机械臂关节角度的变化曲线如图 14所示，可以看出机械臂的实际运动与仿真得到的关节角度的变化情况一致。试验结果表明，相比于传统的机械臂，所设计的超冗余机械臂具有更高的灵活度，可以在复杂的障碍环境中执行任务。

5.2 机械臂写字实验

控制机械臂末端在写字板上写字除了需要合理地规划机械臂末端的运动轨迹外，还需要机械臂末端与写字板之间保持合理的接触力。该实验主要通过阻抗控制算法^[33]以及机械臂的路径规划控制机械臂在写字板上写下“CIOM” 4个字母。实验过程如图 15所示，可以看出机械臂在写字板上依次清晰地写下了“CIOM”，书写过程中没有出现由于机械臂末端接触力的突变而引起书写不清晰的现象。机械臂关节角和关节速度曲线如图 16所示。该实验说明了所设计的机械臂具有良好的力控制能力与轨迹规划能力。

5.3 机械臂恒力保持实验

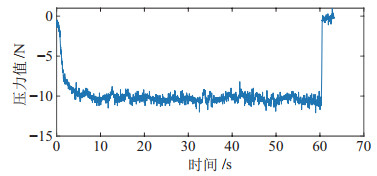
为了说明所设计的机械臂具有精准的恒力保持性能，进行了机械臂的恒力保持实验。该实验需要在机械臂末端接触的外界环境发生变化时，主动调整9个关节的角度使机械臂末端压力保持恒定。首先，将一个充满气的气球固定在UR10机械臂的末端，并在所设计的超冗余机械臂的末端安装一个6维力传感器。力传感器型号为OptoForce HEX-70-XE-200N，力采集周期为0.01 s。接着，使超冗余机械臂末端接触气球，同时UR10机械臂进行不确定的往复运动，通过阻抗控制算法使超冗余机械臂末端与气球之间的接触力保持恒定。实验过程如图 17所示，可以看出，在UR10机械臂进行往复运动的同时，超冗余机械臂也相应地跟随运动。同时，气球的形状在实验过程中并没有发生明显变化。图 18显示了实验过程中超冗余机械臂末端沿水平方向的压力值随时间的变化曲线，可以看出超冗余机械臂在跟随UR10机械臂运动的过程中能够始终将末端与气球之间的压力保持在10 N左右。在机械臂末端与气球之间产生稳定的接触压力后，最大接触压力误差为1.8 N。考虑到压力传感器在测量过程中不可避免地受到噪声的影响，该压力误差值是可以接受的。由此可以看出，通过阻抗控制算法，即使外界环境不断发生变化，所设计的超冗余机械臂末端仍可以精确地保持所给定的压力值不变。

从以上3个实验可以看出，所设计的超冗余机械臂具有穿越复杂障碍环境的优越性能、良好的力控制能力，并能实现与其他机械臂的协同工作。因此，所设计的机械臂具备在复杂的空间环境中执行各种在轨服务的基本能力。

6 结论（Conclusion）

本文针对空间在轨服务任务设计了一种9自由度超冗余模块化空间机械臂，该机械臂由9个相同的关节模块构成，具有穿越复杂障碍环境的能力以及良好的力控制能力。对机械臂关节进行了合理的结构设计，关节内部结构紧凑并能实现最大190 N $ \cdot $ m的扭矩输出。机械臂的伺服控制系统采用位置、速度以及电流的三路回环控制，提高了机械臂的位置控制精度。基于改进的Bi-RRT算法和阻抗控制算法，机械臂在复杂环境中分别进行了避障、写字和力控制实验。实验结果表明，所设计的模块化超冗余机械臂具有灵活的避障能力和良好的力控制能力，能够在复杂空间环境下满足在轨服务任务的基本需求。